复合加固圆形木柱轴心受压承载力计算

阿斯哈，周长东

(北京交通大学 土木建筑工程学院，北京 100044)

作为中国古代历史风貌建筑最主要的结构形式，木结构具有特殊的历史、科学和文化价值。古建筑木柱作为主要支撑上部复杂屋盖结构的竖向受力构件，具有极为重要的建筑和结构作用。考虑到木材是一种古老的生物质建筑材料，在若干年的服役期间极易发生虫蛀、开裂、糟朽等损伤，从而影响木柱的工作性能，进而威胁到整体木结构的稳定性和安全性。因此迫切需要对古建筑木柱进行维修和加固。

碳纤维增强复合材料（carbon fiber reinforced polymer，CFRP）以其轻质、高强、耐腐蚀、易裁剪等特性，近年来被广泛应用于结构加固的研究和工程当中。有学者开展了采用CFRP布加固木柱的试验研究，结果表明，CFRP布可在一定程度上提升木柱的承载和变形能力[1–5]。许清风等[6]采用局部顺纹木块替换原木柱损伤区域，并用CFRP布包裹进行加固，结果表明，木柱的受压承载力和延性可得到完全恢复。采用CFRP布包裹墩接和包镶加固糟朽木柱的试验研究[7–8]表明，该种加固方法可以不同程度地恢复损伤木柱的延性和极限承载力。

淳庆等[9–10]认为：外贴纤维复合材料（fiber reinforced polymer，FRP）加固对木柱承载力的提高程度有限；而内嵌FRP筋（板）则可以有效提升木构件的承载力；嵌入CFRP筋（板）加固后，圆形木柱的轴心受压承载力有不同程度的提升。内嵌筋材加固方法能够提高木柱承载力，外包FRP布可改善木柱延性，采用两者相结合的复合加固方法则可以同时提升木柱的承载和变形能力。为探索复合加固方法的成效，朱雷等[11]采用内嵌FRP筋、外包CFRP布的方法对两根方形木柱进行试验研究，结果表明，加固木柱的承载力和延性均得到改善。但是，上述研究试件数量有限，应对内嵌筋材、外包FRP布复合加固方法的适用性展开更加全面而深入的研究，同时应考虑内嵌筋材种类及木柱截面形状等因素的影响。

周钟宏[12]、袁书成[13]等在FRP布加固木柱试验的基础上，通过系数回归，提出约束木柱承载力计算公式，与试验结果吻合良好。邵劲松等[14–15]通过分析峰值应变比和约束刚度比的关系，提出FRP布加固木柱承载力计算公式，计算值与试验结果对应良好。淳庆等[16]基于试验数据拟合，提出碳–芳纶混杂FRP布加固圆形木柱轴心受压承载力计算公式。上述对FRP布加固木柱承载力计算公式的探索中，大多未综合考虑FRP布的种类和层数、木柱截面的尺寸和形状、试验试件的数量等诸多限制因素，因此，仍需探究可靠的FRP布加固木柱承载力计算公式。既有理论模型多基于FRP布约束木柱而建立，鲜有研究涉及复合加固木柱受压承载力的计算。

综上所述，作者开展复合加固木柱的轴心受压试验研究，旨在探究内嵌钢筋外包CFRP布复合加固方法的适用性；同时，拟合试验数据，提出CFRP布约束木柱的抗压强度计算模型，给出复合加固圆形木柱的承载力计算公式；并通过补充试验和与既有文献中的试验研究结果对比验证其有效性。

1 试验概况

1.1 试件及材料属性

为确定内嵌钢筋外包CFRP布复合加固木柱的承载能力，作者设计制作了12组共42根轴心受压圆形短柱试件；木柱的直径为235 mm，高为800 mm。试件的制作过程为：首先，在木柱表面开槽，其尺寸为24 mm×24 mm；其次，将16 mm直径、800 mm长度的钢筋通过环氧树脂植筋胶粘结于木槽内；待植筋胶硬化后，按照既定位置将浸渍的CFRP布环向粘贴于木柱表面；在恒温恒湿环境中养护7 d，进行轴心受压试验。

表1为试件分组情况。

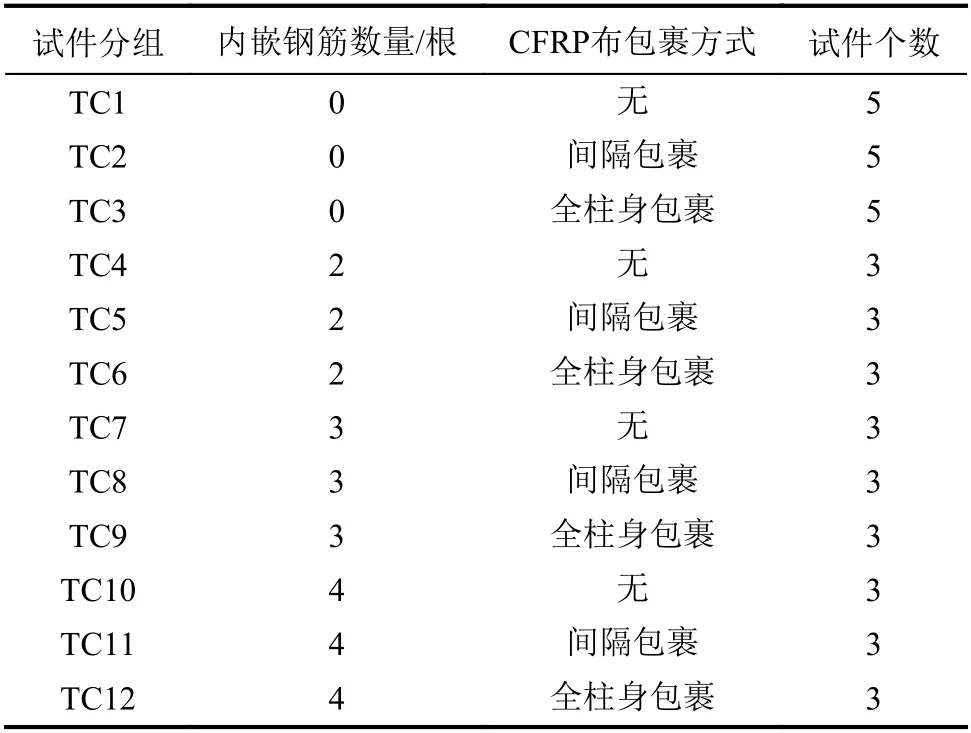
表1 试件分组Tab. 1 Specimen groups

图1中，钢筋牌号为HRB400，直径16 mm；屈服强度和抗拉强度分别为432和579 MPa，弹性模量和极限应变分别为2×105MPa和0.134。CFRP布的两种布置形式绘制于图2，其厚度为0.167 mm，抗拉强度和弹性模量分别为3 521和2.15×105MPa，极限应变为0.016。试验用木材为花旗松，其材料参数通过木材无疵小试样测得。木材的密度和含水率分别为0.56 g·cm–3和11.4%；顺纹抗压强度和弹性模量分别为54.8 MPa和17 440 MPa。

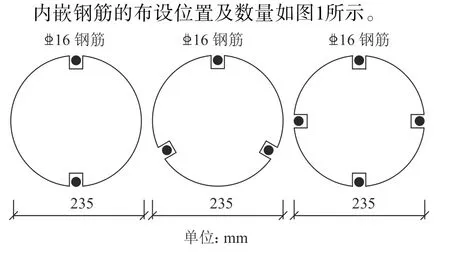
图1 内嵌钢筋布置Fig. 1 Layout of near surface mounted steel bars

图2 CFRP布的布置Fig. 2 Arrangement of CFRP strips

1.2 试验加载及量测方法

轴心受压试验加载通过一台6 000 kN的电液伺服压力试验机完成，加载制度为：首先，采用力控制加载至500 kN，加载速率为1 kN/s；之后，采用位移控制，速率为0.5 mm/min。当试验荷载降至峰值荷载的70%左右时，停止试验。试验装置如图3所示。

图3 试验装置Fig. 3 Test setup

试验荷载由力传感器获得，试件整体位移由布设于木柱两侧的电感式位移计采集。试件中部区段布置了横向和纵向应变片，以得到试验中木材和CFRP布的应变变化规律。同时，CFRP布的应变片布置与木材表面应变片的粘贴位置相一致，具体的应变测点布置如图4所示。试验数据由IMC动态测试系统同步采集获取。

图4 应变测点布置Fig. 4 Measurement points of strain gauges

2 试验结果

2.1 试验现象

当试验荷载接近450 kN时，有轻微的木纹挤压错动声，且随着试验荷载的增加，声响逐渐增大；接近峰值荷载时，木柱发出连续的木纤维撕裂声。初始加载至达到峰值荷载的过程中，除木纹的挤压、错动、撕裂声响外，并无其他明显试验现象。随着加载位移增大，初始缺陷（如木节）处的木材开裂并压溃；靠近该区段的CFRP布出现皱褶进而发生脆性断裂破坏；内嵌钢筋弯曲显著，发生屈曲破坏。试验木柱的破坏主要位于初始缺陷较为集中的区域，柱身其他区段基本完好。

2.2 试件破坏形态

生物质特性所致，木材具有髄心、木节、干缩裂缝等初始缺陷，且难以避免。复合加固木柱的破坏过程和形态较为接近，图5为试验试件典型的破坏形态。

图5 试验试件破坏形态Fig. 5 Failure modes of test specimens

由图5（a）可见：木柱的破坏发生在靠近中部木节较多区域，木材受压变形，产生裂缝并被压溃；在两条CFRP布之间，钢筋发生屈曲破坏，并引发CFRP布的脆性断裂；柱身其他区段则无明显破坏现象。图5（b）～（d）表明，在钢筋和CFRP布发生破坏的区域，木材的初始缺陷较为集中。总结复合加固木柱的破坏形态，由于初始缺陷的影响，木材局部受压承载力不足而发生开裂和变形，进而引起CFRP布的脆性断裂和内嵌钢筋的屈曲。

2.3 试件荷载–位移曲线

图6为试验中各组试件的荷载–位移曲线。由图6可知：内嵌钢筋数量相同的情况下，由没有CFRP布约束，到间隔包裹CFRP布，再到全柱身粘贴CFRP布，试验试件的峰值荷载及延性均有显著提升，表明外包CFRP布可改善木柱的受压承载力和变形能力；比较CFRP布包裹形式相同的各组试件，随着内嵌钢筋数量的增加，试件的峰值荷载得到提升，表明内嵌钢筋可以协同木柱承受竖向荷载；由于钢材是一种较好的延性材料，因此钢筋能够一定程度地提升木柱的延性，但是作用并不突出。钢筋的承压作用能够减缓木材的横向变形，从而间接协助CFRP布约束木材，以提升木柱的承载力；CFRP布的约束作用可以防止钢筋过早屈曲，使其有效地发挥承压作用。

图6 试件荷载–位移曲线Fig. 6 Load–displacement curves of specimens

3 复合加固木柱承载力计算公式

3.1 CFRP约束木柱顺纹抗压强度计算模型

类比经典箍筋约束及FRP约束混凝土理论[17–18]，作者提出式（1）所示的CFRP布约束木柱的抗压强度计算模型：

式中，fcc为CFRP布约束木柱的顺纹抗压强度，fco为未加固木柱的顺纹抗压强度，k为CFRP布有效约束系数，fl为CFRP布侧向约束应力。

试验中CFRP布的包裹形式采用间隔包裹和全柱身包裹两种方式，因此，需要考虑CFRP布的间隔对其约束作用的削减。效仿箍筋以及FRP材料约束钢筋混凝土柱的计算模型[19–20]，可将木柱截面分为有效约束区和无效约束区。图7为CFRP布加固木柱有效约束区示意图，其中bf为CFRP布的宽度。相邻CFRP布之间的无效约束区分布为近似拱作用模式的二次抛物线，该曲线的初始切线与水平方向呈45°。CFRP布粘贴区域对木柱的约束作用最强，而相邻CFRP布条之间拱作用曲线顶点位置处木柱截面受到的约束最为薄弱。因此，取该截面为加固木柱受压承载力计算的控制截面，有效约束区面积按照式（2）进行计算：

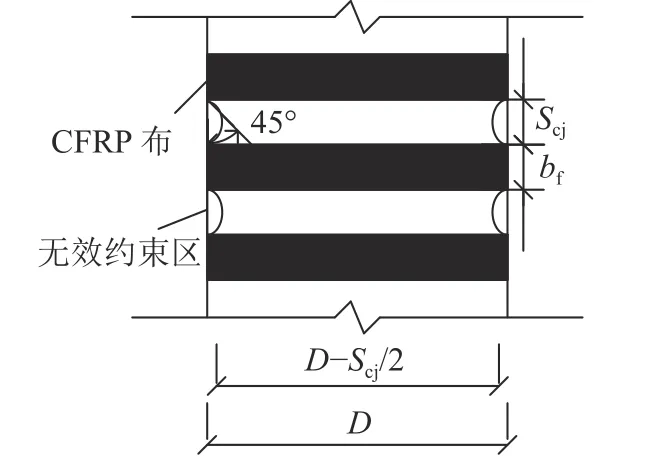
图7 CFRP布约束木柱有效约束区Fig. 7 Confinement effectiveness area of timber columns strengthened with CFRP strips

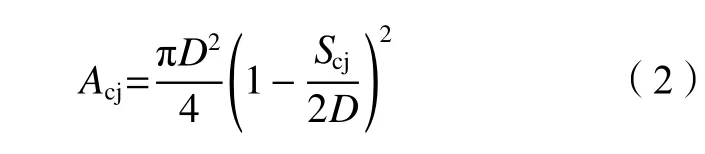
式中，Acj为木柱控制截面有效约束区面积，D为加固木柱直径，Scj为CFRP布净距。

引入控制截面有效系数ks，考虑CFRP布间隔对于约束作用的削弱。控制截面有效系数的计算如式（3）所示：

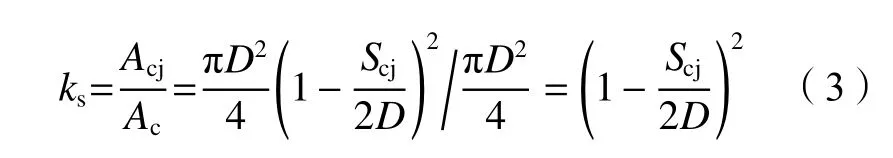
式中，A为木柱的截面面积。

当试验荷载达到峰值时，由于木柱的横向变形，CFRP布对木柱产生水平方向的约束作用，受力分析如图8所示。图8中，fl为CFRP布对木柱的侧向约束应力，tf为CFRP布的厚度，fCFRP为CFRP布的拉应力。

图8 CFRP布约束木柱受力分析Fig. 8 Stress analysis of confinement of CFRP strips

由力的平衡可以得到式（4）：

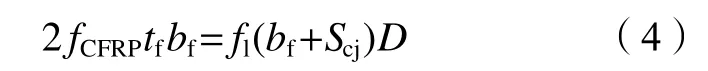
基于式（4）及截面有效系数ks，可得CFRP布侧向约束应力计算式（5）：

依据上述各式，给出3种获得CFRP布约束木柱顺纹抗压强度计算模型的方法。

方法1：基于试验数据可得加固木柱和未加固木柱的抗压强度fcc及fco，结合CFRP布对木柱的侧向约束应力计算式（5），可对CFRP布有效约束系数k进行拟合，具体计算如式（6）所示。将拟合得到的k值代入式（1）便可得到CFRP布约束木柱顺纹抗压强度计算模型。

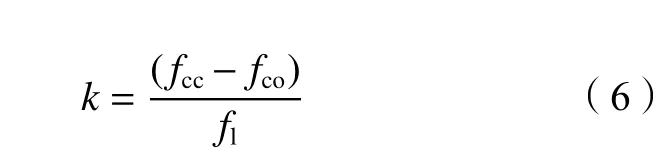
方法2：Zhou[20]、Matthys[21]等提出有效约束系数k是CFRP布侧向约束应力与未加固试件竖向抗压强度比值fl·fco–1的函数。因此，以式（6）计算得到的有效约束系数k为因变量，并以fl·fco–1为自变量拟合确定式（7）中参数α、β的数值。将式（7）拟合结果代入式（1），得到CFRP布加固木柱的顺纹抗压强度计算公式（8）：

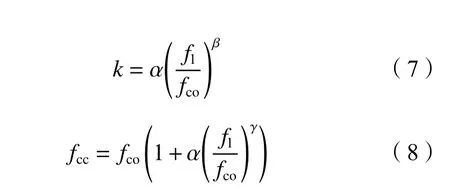
方法3：采用试验数据直接对式（8）中的参数α和γ进行拟合，进而得到CFRP布约束木柱的顺纹抗压强度计算模型。

应用上述3种方法，作者对试验数据进行拟合计算。图9为依据式（6）对约束系数k的拟合结果；图10为基于式（7），以fl·fco–1为自变量，k值为因变量得到的拟合结果；图11为对式（8）中参数α和γ的直接拟合结果。

图9 式（6）拟合结果Fig. 9 Fitting results of equation (6)

图10 式（7）拟合结果Fig. 10 Fitting results of equation (7)

图11 式（8）拟合结果Fig. 11 Fitting results of equation (8)

根据上述拟合结果，得到式（9）～（11），即3个CFRP布约束木柱抗压强度计算模型。

3.2 复合加固木柱轴心受压承载力计算公式

采用表面内嵌钢筋外包CFRP布的方法对圆形木柱进行复合加固，其轴心受压承载力计算应考虑未加固木柱自身承载力和CFRP布对木柱的约束作用，以及钢筋的轴向受压作用。为简化计算，对上述承压作用进行线性叠加，得到复合加固木柱轴心受压承载力计算式（12）。

式中：Nu为复合加固木柱轴心受压承载力，Ncc为CFRP布约束木柱轴心受压承载力，Ns为木柱内嵌钢筋受压承载力。

CFRP布加固木柱的承载力计算为：

式中：fcc为CFRP布加固木柱的轴心抗压强度，采用式（9）～（11）进行计算；A为木柱的截面面积，考虑到内嵌钢筋数量较少，因此，忽略表面开槽对木柱截面的削弱。

按式（14）计算内嵌钢筋的受压承载力：

式中，fy为钢筋的屈服强度，As为内嵌钢筋的承压面积总和。

参考既有研究[22–23]可知，当试件达到峰值荷载时，采用CFRP布加固混凝土圆柱，CFRP布并未达到极限拉应变。因此，定义有效拉应变系数为试件峰值荷载时CFRP布环向拉伸应变与其材料极限拉伸应变的比值，并且有效拉应变系数集中在0.55～0.70的区间内。当采用CFRP布环向粘贴加固圆形木柱时，试验现象表明木材的横向膨胀较混凝土并不显著[15]。依据试验中各组试件峰值荷载时，CFRP布应变量测结果的平均值，本文采取有效拉应变系数为0.125。

将不同CFRP布加固木柱抗压强度计算式（9）～（11）分别代入式（13），以及所得计算联合式（14）分别代入式（12），可得采用不同抗压强度模型的复合加固木柱轴压承载力计算值。图12为承载力计算结果与试验值的比值分布。

图12中横坐标为试验试件，共列入27根加固木柱的计算结果。比较图12中的散点分布区域不难发现，采用式（11）进行复合加固木柱承载力计算时，计算结果更接近试验值，因此，推荐式（11）为CFRP布约束木柱抗压强度计算公式。继而，确定内嵌钢筋外包CFRP布复合加固木柱的轴心受压承载力计算式，如式（15）所示：

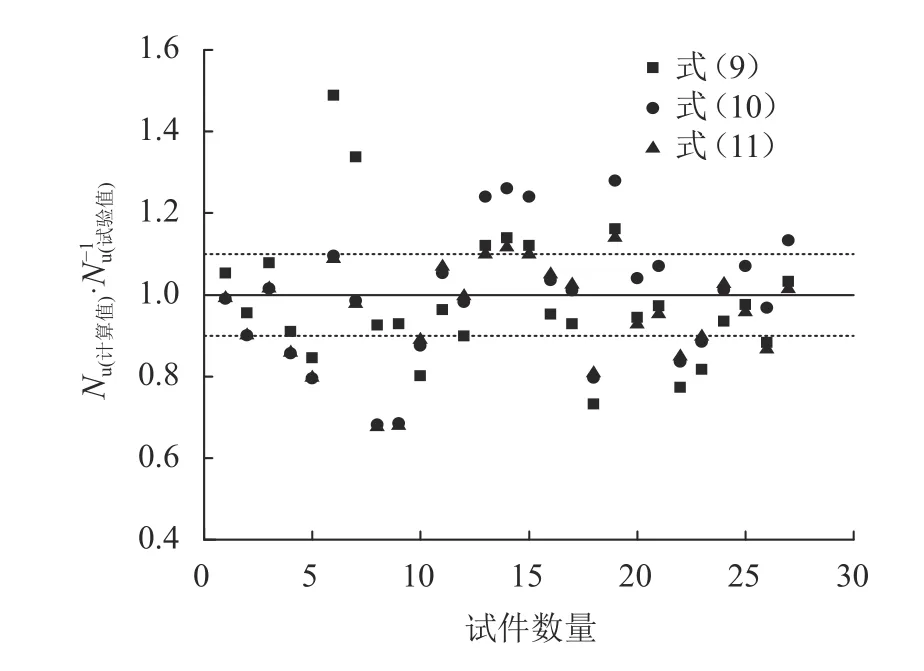
图12 不同抗压强度模型Nu计算值与试验值比较Fig. 12 Comparison between Nu theoretical and experimental results for different strength models

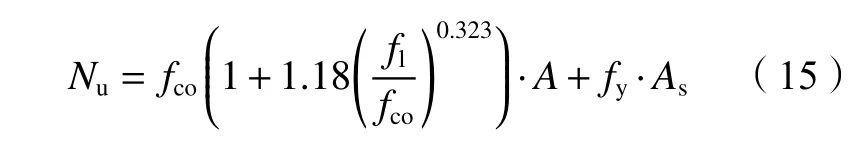
4 承载力计算模型验证

4.1 承载力计算式可靠性验证

通过改变钢筋直径和数量，进而改变内嵌钢筋配筋率，来验证式（15）的可靠性。试验共设计3组9根复合加固木柱试件，其中，木柱直径为235 mm、高800 mm，与本文初始试验试件尺寸相一致，木柱均采用CFRP布的间隔包裹形式（图2（a）），内嵌钢筋直径为20 mm；3组试件分别内嵌有2、3和4根钢筋；试件制作完成之后，经与初始试验相同条件的养护，进行轴心受压试验。式（15）计算得到的承载力与试验结果列于表2。

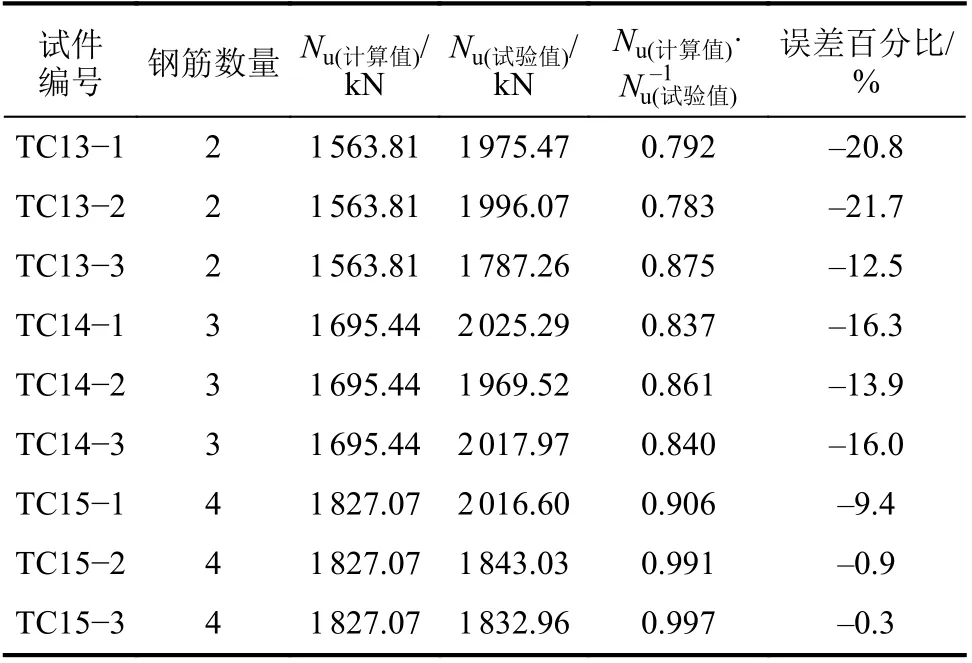
表2 复合加固木柱Nu计算值与试验值对比Tab. 2 Comparison between Nu theoretical and experimental results of composite strengthened timber columns

由表2复合加固木柱的计算和试验结果对比可知，式（15）可以较好地预测复合加固木柱的轴心受压承载力。需要说明的是，在验证试验中，TC13组木柱的木纹较初始试验试件以及其他组试件的木纹更为密集，由木材材料性能可知该组木柱受压承载力可能偏高。试验结果反映出这一组试件材料性能的离散性。木材作为一种生物质的建筑材料，其自身存在显著的离散特性，而本文提出的复合加固木柱承载力计算方法可将计算结果控制在15%的误差范围之内，因而，具有较好的计算效果。

4.2 承载力计算与试验研究[1–5]结果的对比

为了进一步验证所给出的复合加固木柱轴心受压承载力计算公式的可靠性，计算既有文献[1–5]中CFRP布加固木柱的承载力理论值，并与试验结果进行对比。虽然目前有较多采用FRP材料加固木柱的试验研究，但是式（15）的提出是以单层CFRP布加固圆形木柱为条件的，因此仅选取与本文加固工况相近的试验研究进行对比分析。而对考虑FRP的种类和层数、木柱截面形状等因素的承载力计算公式，有待进一步研究。除此之外，目前国内外鲜有采用内嵌钢筋外包CFRP布复合加固圆形木柱的研究，所对比的既有文献[1–5]中，圆形试验木柱均仅采用CFRP布进行加固。

图13为由式（15）所得加固木柱的承载力计算值与既有文献[1–5]中加固木柱试验值的对比图中，百分比为理论计算值与既有文献测验结果的误差。不难发现针对不同的试验研究，理论计算值与试验值较为接近，具有良好的对应关系。计算值仅与张天宇[1]的试验值相差较大，由于张天宇试验研究中的木柱截面尺寸较小，因而，尺寸效应可能导致上述偏差。由图13中理论计算与试验值的对比结果可知，式（15）可以有效预测加固木柱的轴心受压承载力，进而能够为上述复合加固方法在工程中的应用提供理论依据和实际指导。

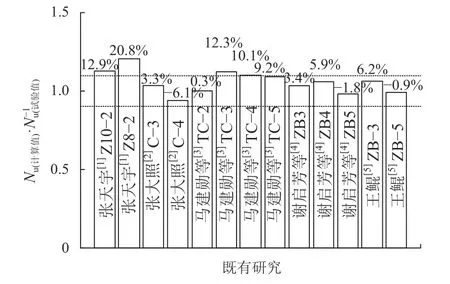
图13 承载力计算值与试验值[1−5]的对比Fig. 13 Comparison between theoretical bearing capacity and experimental values of reference[1−5]

5 结 论

完成42根复合加固木柱的轴心受压试验，描述破坏现象，得到试件的荷载–位移曲线；提出CFRP布约束木柱顺纹抗压强度计算模型，给出复合加固木柱轴压承载力计算公式；验证承载力计算式（15）的可靠性。得到结论如下：

1）木材的木节等初始缺陷不可避免，而复合加固木柱的破坏主要发生于初始缺陷（木节）集中区域；随着木材发生显著的变形和开裂，CFRP布脆性断裂，钢筋屈曲，随即加固木柱发生破坏。

2）由试件的荷载–位移曲线可知，内嵌钢筋外包CFRP布的复合加固方法可以有效提升木柱的承载和变形能力；CFRP布可与内嵌钢筋相互促进、协同工作，共同提升木柱的抗压性能。

3）基于经典的CFRP布约束混凝土柱轴心抗压强度理论，通过参数拟合提出3种CFRP布约束木柱的顺纹抗压强度计算模型。

4）通过理论值与试验值的对比，比选出适用于CFRP布约束木柱的抗压强度计算模型，进而给出复合加固木柱轴心受压承载力计算公式。

5）补充试验和理论计算的对比结果表明，理论公式（15）可将计算结果控制在15%的误差范围之内，具有较好的预测效果；由理论计算值与既有研究中试验值的对比可知，式（15）能够预测加固木柱的受压承载力，验证了实际应用的可靠性。

6）所提出的复合加固木柱轴心受压承载力计算公式具有一定的局限性，对于考虑纤维布的种类和层数、木柱截面的尺寸和形状等因素的计算公式，有待进一步的研究与分析。