多光谱图像变换域统计量移位鲁棒无损信息隐藏*

刘娟妮，周 诠，李小军，方 海

(西安空间无线电技术研究所 空间微波技术国家级重点实验室，西安 710100)

1 引言

目前，信息隐藏技术主要应用于多媒体信息认证、知识产权保护及隐蔽传输等信息安全领域，其载体包括静止图像、音频、视频、文本等多种媒介。多光谱图像作为卫星遥感的主要数据，具有广泛的应用，以多光谱图像为载体的信息隐藏技术越来越受到关注。

现有多光谱图像信息隐藏技术以水印为主［1－2］，存在隐藏容量小，嵌入信息不能盲提取以及载体图像不能无损恢复等问题。虽然已有一些无损方法可以实现这种可逆性［3］，但是这些方法无损恢复的前提是含密图像不能遭受任何攻击，否则信息就不能正确提取。实际中多光谱图像的传输很可能受到噪声干扰或者被压缩，例如SPOT 4 和IKONOS卫星在数据传输前进行了有损压缩［4］。因此多光谱图像信息隐藏不仅要求对载体图像的破坏要小，还要考虑对压缩以及噪声的鲁棒性。为了解决这个问题，提出了鲁棒无损信息隐藏方法，即在含密图像未受到攻击时，载体图像和秘密信息都可以精确恢复;当载体图像在传输过程中遭受有损压缩或噪声干扰时，秘密信息仍然可以正确提取。

Ni 等人［5］基于patchwork 理论提出了一种基于统计量的鲁棒无损信息隐藏方法，能够抵抗JPEG和JPEG2000 压缩攻击，但是该方法嵌入容量较小。Zeng 等［6］对Ni 的方法进行改进，提出一种基于图像块算术差的统计量，通过统计量直方图移位将信息嵌入到图像块内。该方法可以抵抗JPEG 压缩攻击，和Ni 的方法相比，Zeng 的方法在嵌入容量和鲁棒性上均有很大改进。李晓博和周诠［7］使用与文献［6］相同的统计量，通过引入一些阈值进一步改进了Zeng 方法的性能。朱厉洪和周诠［8］通过图像预处理实现整数离散余弦变换(Discrete Cosine Transform，DCT)域的鲁棒无损信息隐藏，获得了较好的图像质量。An 等［9］也提出了一种基于统计量的方法，并引入K 均值聚类方法来确定嵌入区域，提高了鲁棒性。然而，An 的方法采用属性启发式像素调整的方法来防止溢出，需要将改变的像素作为边信息进行传输，因此该方法不能盲提取嵌入信息。Yang 和Lin［10］通过系数移位提出了一种大容量的鲁棒无损隐藏算法，在信息嵌入过程中需要用定位图来记录像素是否移动，这也是一个非盲算法。

上述鲁棒无损信息隐藏方法在鲁棒性和不可见性上已有很大提高，但这是建立在非盲提取的基础上，现有盲提取算法嵌入容量仍然较小，给实际应用造成困难。因此，本文联合卡洛南－洛伊变换(Karhunen Loêve Transform，KLT)和离散小波变换(Discrete Wavelet Transform，DWT)，以小波HH 系数分块均值为统计量进行信息隐藏，实现秘密信息盲提取，并利用误差补偿的方法无损恢复载体。

2 统计量移位鲁棒无损信息隐藏

2.1 统计量

设载体多光谱图像的大小为Nx×Ny×Z，其中Z 为频段数。在数据嵌入前先进行光谱方向KLT变换，获取多光谱图像KLT 本征子图像。设V(KLT，z)是多光谱图像第z 个KLT 本征子图像，V(DWT，z)是V(KLT，z)的DWT 变换，1≤z≤Z。将V(DWT，z)的HH 高频子带分成大小为m× n 不重叠的块(m、n 为偶数)，则频段z 内HH 高频子带各块均值α 为

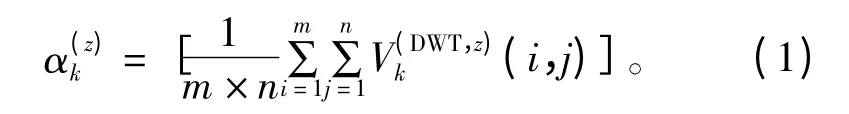
式中，k 是块索引，1≤k≤Nx×Ny/(2×m×2×n)，是位置(i，j)处的小波变换系数值，符号［·］表示取整。在有损压缩或者噪声攻击下，是一个比较稳定的值，变化量很小，因此可以将作为统计量，利用的稳定性来嵌入信息。

KLT 是统计意义上去相关性的最优变换［11］。由于多光谱图像各谱段间相关性很强，对其进行KLT 变换可以将大部分信号能量集中分布在前几个本征子图像，然后进行DWT 变换又将KLT 本征子图像的能量集中在低频子带。因此，在小波变换HH 高频子带中隐藏信息对载体的影响很小，保证含密图像具有较好的视觉质量。同时，将HH 高频子带分块均值作为统计量，是由于不同图像其取值基本保持不变，而且即使含密图像在传输过程中受到压缩和噪声攻击时，该统计量的值也变化很小，所以该统计量具有较强的鲁棒性。

图像“Robinson Farm”的统计量α 直方图分布如图1 所示，其中，m=2，n=2，z=6;X 轴代表α 的值，Y 轴是α 的数量。从图1 中可知，α 取值集中于［－4，3］，可以通过将统计量α 左右移位来嵌入秘密信息。

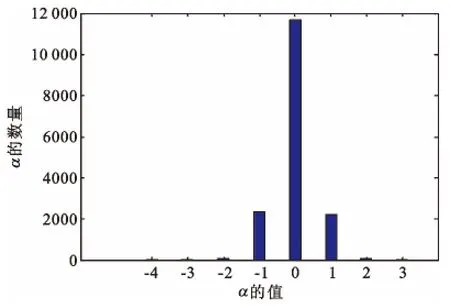
图1 α 的直方图分布Fig.1 Histogram of α

2.2 数据嵌入过程

对载体多光谱图像，按KLT 本征子图像分别嵌入信息。对各本征子图像，计算上述统计量，然后统计其直方图分布，并确定公式(4)中参数T。

依次扫描小波高频系数各分块，在每个分块中嵌入1 b秘密信息。对于各个分块，如果嵌入的秘密信息为0，则块内元素保持不变;如果嵌入的秘密信息为1，通过调整α 来嵌入，规则如下:

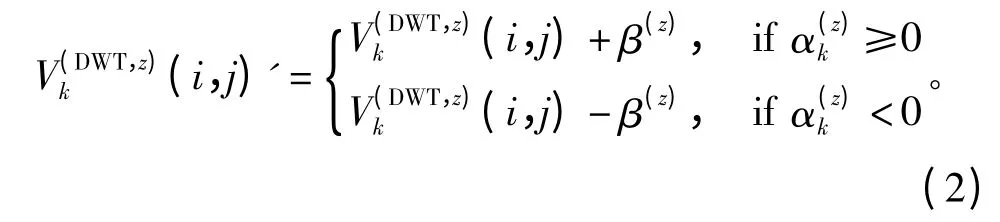
式中，z 表示KLT 本征子图像的序号;

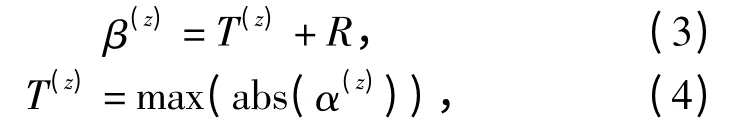
R 为引入的正整数参数，称之为鲁棒空间。R 是嵌入秘密信息为0 的区域(简称“嵌入0 区”)和嵌入秘密信息为1 的区域(简称“嵌入1 区”)的间隔，R越大意味鲁棒性越强。

将各V(DWT，z)'通过逆DWT 和逆KLT 变换来生成含密图像，嵌入过程如图2(a)所示。

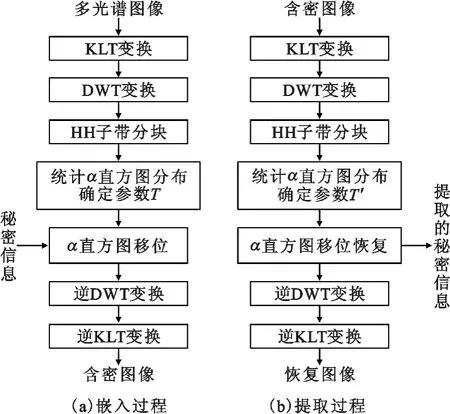
图2 信息嵌入和提取过程Fig.2 Flowchart of data embedding and extracting process

秘密信息依次嵌入到从KLT 本征子图像B 到本征子图像Z 的小波HH 高频子带的每个分块中，且每个分块嵌入信息数为1 b，因此，对于大小为Nx×Ny×Z 的多光谱图像，若分块大小为m×n，则嵌入容量为

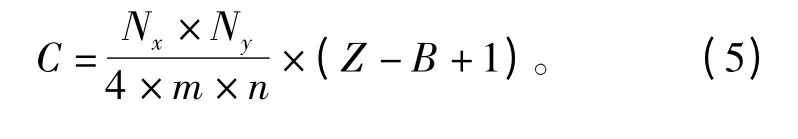
2.3 数据提取过程

含密图像在传输过程中可能被压缩或者受到噪声攻击，此种情况α 的分布会发生变化，嵌入1 区和嵌入0 区可能有所交叠，使信息在提取时出现误码。为了正确的提取数据，本文采用文献［6］的方法并做了适当修改。

数据提取和图像恢复过程如下:

首先对含密图像进行KLT 变换，生成含密图像的KLT 本征子图像。对嵌入数据的KLT 本征子图像进行DWT 变换，获取DWT 系数矩阵V(DWT，z)'，计算HH 高频子带的统计量α，统计α 的直方图分布，并获取参数T'。新的嵌入0 区的边界T'可以用嵌入0 的数目N0来确定，即保证在［－T'，T'］区间内α的数目Nα等于N0，即{Nα=N0|－T'≤α≤T'}。

使用式(6)从α 的统计直方图中提取嵌入数据:

将V(DWT，z)进行逆小波变换，得到所有KLT 本征子图像后，再进行KLT 逆变换来重建载体多光谱图像，整个提取过程如图2(b)所示。

2.4 载体误差补偿

KLT 和DWT 均为浮点数变换，正变换和反变换是不可逆的。在含密多光谱图像未受到攻击时，为了达到载体无损恢复的目的，将浮点数变换以及像素值溢出引起的误差用文献［12］的方法嵌入含密图像中，用于对载体图像进行误差补偿。具体过程如图3 所示:首先利用2.2 节方法嵌入秘密信息得到含密图像1，然后利用2.3 节方法恢复载体多光谱图像，将恢复图像和原始载体多光谱图像的差值图像采用行程编码压缩。由于差值图像绝大部分像素值为0，压缩码流数据量很小，将压缩码流以无损信息隐藏的方式嵌入含密图像1 中得到含密图像2，将其作为最终输出的含密图像。

在接收端，首先提取误差压缩后的码流并得到含密图像1，对压缩码流解码得到误差图像，然后进行秘密信息提取和载体图像恢复，最后将恢复的载体图像与误差图像相加重构原始载体图像。

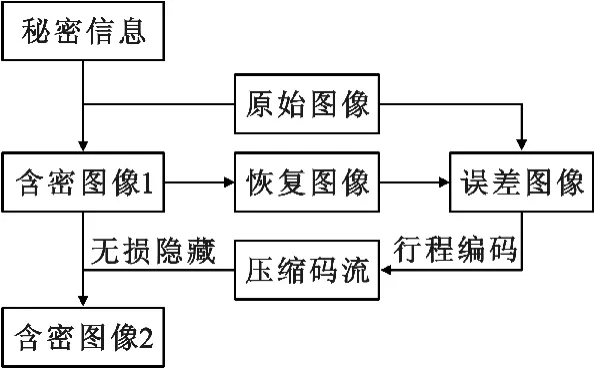
图3 误差隐藏过程Fig.3 Process of error embedding

3 实验结果

实验采用美国马里兰大学公开的Landsat 卫星多光谱图像(http://glcf.umd.edu/data/)来测试本文算法性能。实验平台为Matlab R2011a，主频为2.50 GHz，内存大小为2 GB。测试图像包含6 个频段，空间分辨率30 m，每一个频段包括512×512 个像素，每个像素8 b精度。测试图像的频段3 如图4所示。实验中的秘密数据为二进制伪随机数序列，HH 子带矩阵分块大小为2×2。秘密数据的嵌入是从第B(B 为4、5、6)频段到第6 频段，B 的大小决定隐藏容量C，R 影响鲁棒性和视觉质量。

图4 测试图像Fig.4 Test images

3.1 不可见性

用各频段峰值信噪比(Peak Signal－to－Noise Ratio，PSNR)的平均值来度量多光谱图像的失真。频段z 的PSNR 如式(8)～(9)所示:

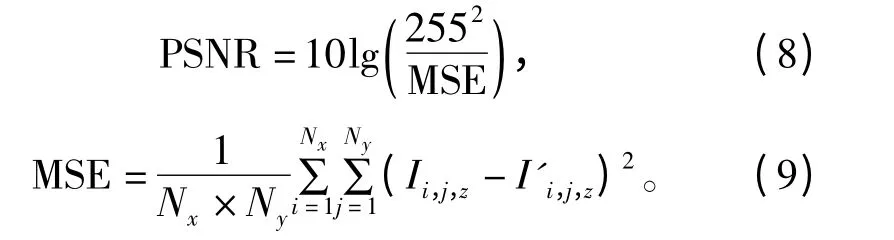
式中，Ii，j，z和分别表示多光谱图像I 和含密多光谱图像I'第z 频段位置(i，j)处的像素值。

鲁棒空间R 影响图像质量，图像“Robinson Farm”的PSNR 和鲁棒空间R 的关系如图5 所示。在R=9，B 分别为4、5、6 时，图像的PSNR 分别为38.42 dB、40.23 dB、45.69 dB，这说明在鲁棒空间R 相同时，嵌入容量越小，图像PSNR 越高。另外，3条曲线的分布规律均表明，PSNR 会随着鲁棒空间R的增加而减小。其他测试图像也得到类似的结果。

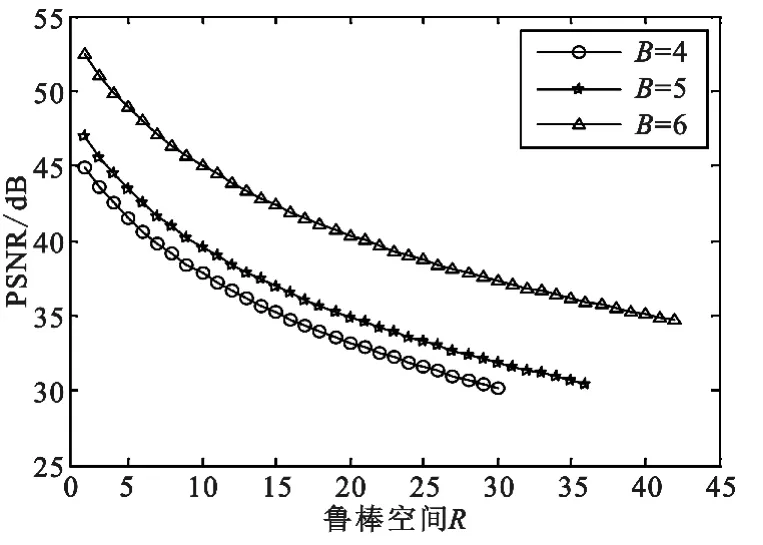
图5 鲁棒空间R 和PSNR 的关系(Robinson Farm)Fig.5 Relationship between robust space R and PSNR (Robinson Farm)

用平均光谱角(Mean Spectral Angle，MSA)来衡量光谱失真，平均光谱角是光谱角制图(Spectral Angle Mapper，SAM)的平均值。光谱角制图是像元原始光谱矢量和含密光谱矢量之间的夹角［13］:

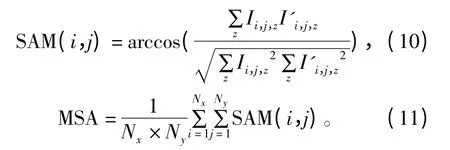
图像“Robinson Farm”的MSA 和鲁棒空间R 的关系如图6 所示。在三种容量条件下，MSA 均随着R 的增加而增加，也即鲁棒空间R 越大，光谱失真也越大。

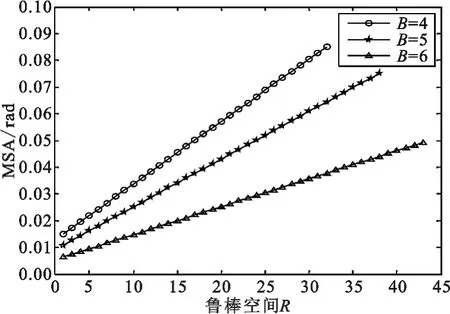
图6 鲁棒空间R 和MSA 的关系(Robinson Farm)Fig.6 Relationship between robust space R and MSA (Robinson Farm)

3.2 无损恢复

为了能够无损恢复原始图像，本文将因浮点数变换以及像素溢出造成的误差用游程编码压缩后用无损隐藏的方法嵌入到含密图像中，在含密图像没有遭受攻击时误差信息可以无失真地提取，从而补偿恢复载体的误差。

表1 给出了不同嵌入容量下误差图像经过行程编码后的比特数(Prediction Error Bits，PEB)。在嵌入容量较低时，各测试图像PEB 均小于100;在嵌入容量较大时(B=4)，各测试图像的PEB 有所增加，其中图像“Lawrence”和“San Francisco”增加比较明显。这也说明随着嵌入容量增加，图像的不可见性会变差，但是本文方法即使嵌入容量较大时(B=4)，含密图像PSNR 仍可达到38 dB左右。

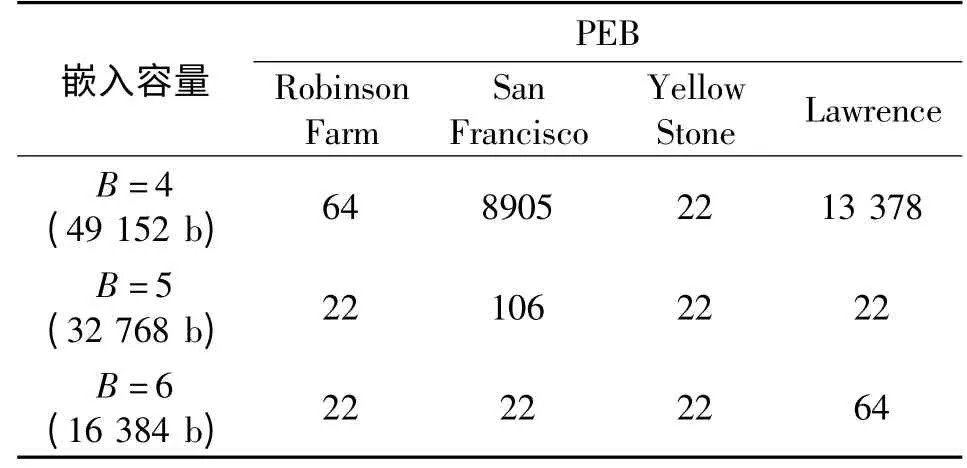
表1 嵌入容量和PEB 的关系(R=20)Table1 Relationship between hiding capacity and PEB(R=20)

3.3 鲁棒性测试

3.3.1 压缩攻击

JPEG2000 是多光谱图像常用的压缩方法。为了测试算法抗压缩性能，采用JASPER 软件，通过逐渐增加JPEG2000 压缩比来压缩测试图像。表2 和表3 给出了满足误比特率(Bit Error Rate，BER)小于1%和PSNR 大于38 dB条件时，分别将HH 子带系数划分为2×2 和4×4 不重叠的块时，本文算法的隐藏性能。压缩比Rc是满足这些条件时可以获得的JPEG2000 最大压缩比。

表2 本文算法在不同容量时的性能(2×2，BER ＜1%，PSNR ＞38 dB)Table 2 Performance of the proposed method with different capacity(2×2，BER ＜1%，PSNR ＞38 dB)

表3 本文算法在不同容量时的性能(4×4，BER ＜1%，PSNR ＞38 dB)Table 3 Performance of the proposed method with different capacity(4×4，BER ＜1%，PSNR ＞38 dB)

系数矩阵分块大小对算法的性能有影响。由表2 和表3 对比可见，在保证图像视觉质量相当的情况下，图像分块越大，秘密信息抗JPEG2000 的压缩比越大，然而，随着分块大小的增加，隐藏容量会降低。因此，在实际使用时可根据具体要求进行分块大小的选择。为了获得较大隐藏容量，本文后续实验选择分块大小为2×2。

3.3.2 噪声攻击

采用不同噪声密度的椒盐噪声攻击来测试算法对噪声的鲁棒性，结果如图7 所示。随着R 的增加，提取信息的误比特率不断降低。调整R 取值可以使提取的秘密信息误比特率控制在0.05 以内。在实际应用中，可以根据需要调整参数R 和B 达到 PSNR、隐藏容量以及鲁棒性之间的均衡。

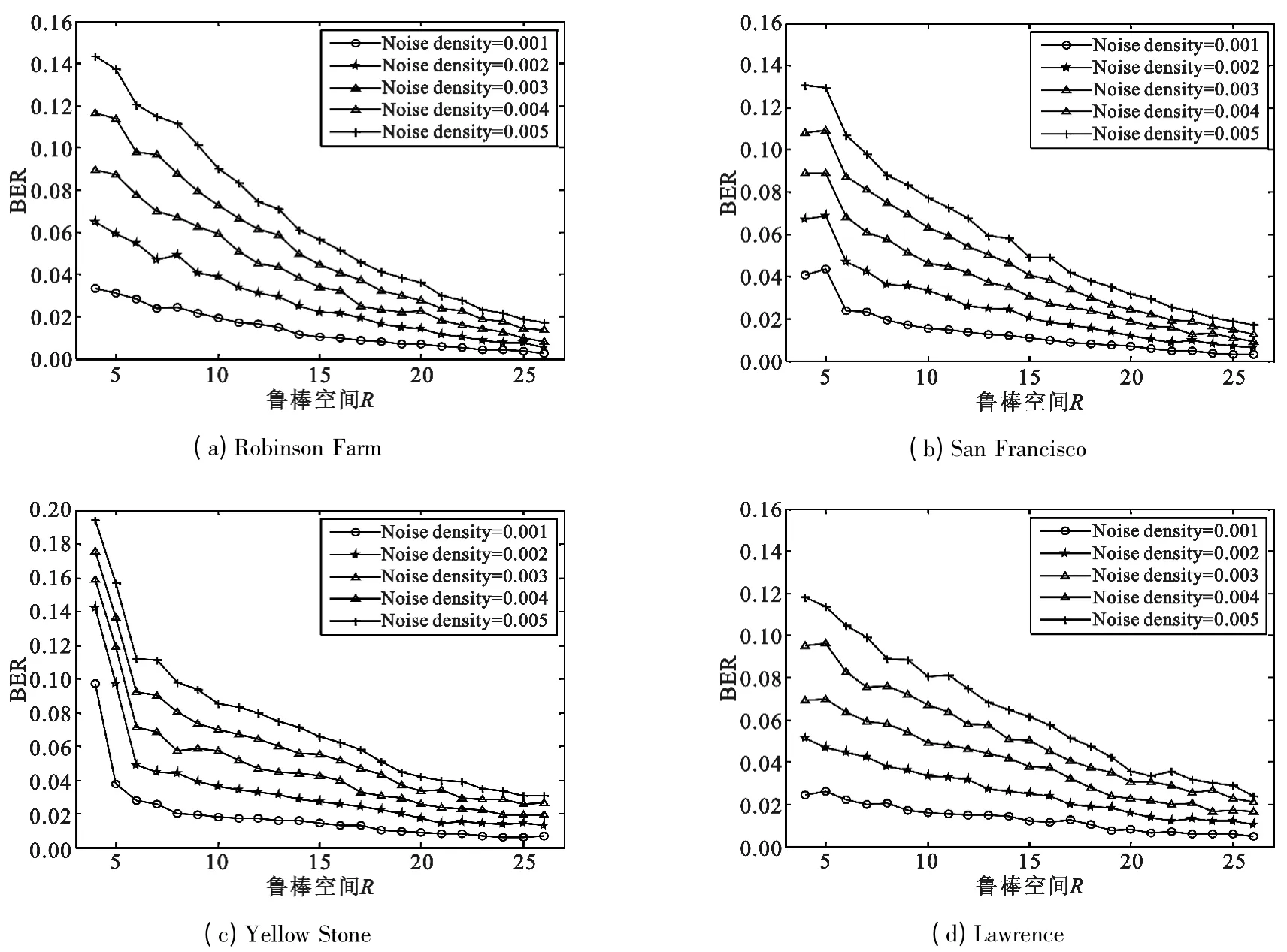
图7 不同椒盐噪声密度下BER 和鲁棒空间R 的关系Fig.7 Relationship between BER and robust space R with different salt and pepper noise density

3.4 和当前算法比较

表4 和表5 分别给出了以多光谱图像和自然图像为载体进行信息隐藏时本文算法和现有算法的对比结果。与Zeng 等人［6］算法和李等人［7］算法相比，在同等不可见性条件下，本文算法的嵌入容量是对比算法的2 倍。另外，本文算法不仅在对抗JPEG2000压缩的鲁棒性方面具有优势，而且对噪声干扰也具有鲁棒性，而文献［6－7］没有讨论对噪声的鲁棒性。

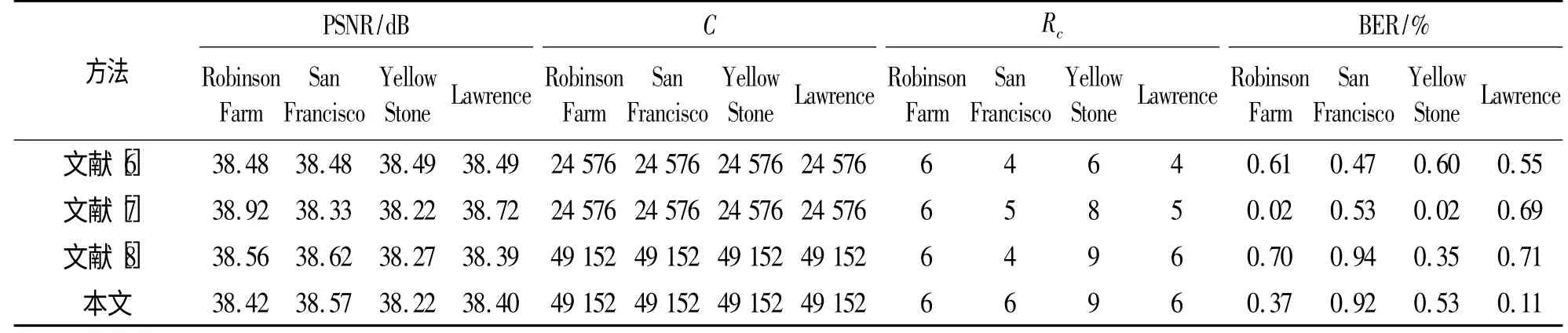
表4 和现有方法的性能对比——多光谱图像(BER ＜1%)Table 4 Performance comparison between the proposed method and existing algorithms for multispectral images (BER ＜1%)

表5 和现有方法的性能对比——自然图像(BER ＜1%)Table 5 Performance comparison between the proposed method and existing algorithms for natural images (BER ＜1%)

同时，该算法与文献［8］对比结果表明，在隐藏容量相同的情况下，本文算法抗JPEG2000 压缩倍数平均比文献［8］高23.9%，误码率平均低44.8%，说明本文算法鲁棒性更好。

4 结束语

本文提出一种变换域统计量移位的多光谱图像鲁棒无损信息隐藏算法，将信息嵌入多光谱KLT 本征子图像的DWT 高频分块系数中，利用小波HH 高频系数分块均值的稳定性实现对压缩和噪声的鲁棒性。实验结果表明:在图像质量与文献［6－7］相当的情况下，该算法隐藏容量是对比算法的2 倍;在隐藏容量与文献［8］算法相同的情况下，该算法抗压缩倍数更高，鲁棒性更好。此外，该算法利用误差补偿使载体图像无损恢复的同时可以盲提取秘密信息，且隐藏容量固定可预知，因此具有较高的实用价值。在实际应用中可以根据需要通过调整参数R、B以及分块大小来达到含秘图像质量、隐藏容量以及鲁棒性之间的均衡。如何在保证算法同等鲁棒性和不可见性的前提下进一步提高信息隐藏容量，还有待继续研究。

［1］KAARNA A，PARKKINEN J.Multiwavelets in watermarking spectral images［C］// Proceedings of 2014 IEEE International Geoscience and Remote Sensing Symposium.Anchorage，AK:IEEE，2004:3225－3228.

［2］FANG H，ZHOU Q，LI K J.Robust watermarking scheme for multispectral images using discrete wavelet transform and Tucker decomposition［J］.Journal of Computers，2013，8(11):2844－2850.

［3］ZHANG X P.Reversible Data hiding with optimal value transfer［J］.IEEE Transactions on Multimedia，2013，15(2):316－325.

［4］PENNA B，TILLO T，MAGLI E，et al.Transform coding techniques for lossy hyperspectral data compression［J］.IEEE Transactions on Geoscience and Remote Sensing，2007，45(5):1408－1421.

［5］NI Z C，SHI Y Q，ANSARI N，et al.Robust lossless image data hiding designed for semi－fragile image authentication［J］.IEEE Transactions on Circuits and Systems for Video Technology，2008，18(4):497－509.

［6］ZENG X T，PING L D，PAN X Z.A lossless robust data hiding scheme［J］.Pattern Recognition，2010，43(4):1656－ l667.

［7］李晓博，周诠.统计量移位的鲁棒无损图像信息隐藏［J］.中国图象图形学报，2012，17(11):1359－1366.LI Xiaobo，ZHOU Quan.Robust lossless image data hiding with statistical quantity shifting［J］.Journal of Image and Graphics，2012，17(11):1359－1366.(in Chinese)

［8］朱厉洪，周诠.卫星遥感图像的鲁棒无损数据隐藏传输算法［J］.宇航学报，2015，36(3):315－323.ZHU Lihong，ZHOU Quan.A robust lossless data hidden transmission method for satellite remote sensing image［J］.Journal of Astronautics，2015，36(3):315－ 323.(in Chinese)

［9］AN L L，GAO X B，LI X L，et al.Robust reversible watermarking via clustering and enhanced pixel－wise masking［J］.IEEE Transactions on Image Processing，2012，21(8):3598－3611.

［10］YANG C Y，LIN C H.High－quality and robust reversible data hiding by coefficient shifting algorithm［J］.ETRI Journal，2012，34(3):429－438.

［11］方凌江，粘永健，王迎春.基于分类KLT 的高光谱图像压缩［J］.计算机技术与发展，2013，23(11):82－85.FANG Lingjiang，NIAN Yongjian，WANG Yingchun.Hyperspectral images compression based on classified KLT［J］.Computer Technology and Development，2013，23(11):82－85.(in Chinese)

［12］方海，周诠.多层嵌入的多光谱图像可逆信息隐藏算法［J］.计算机应用，2013，33(6):1622－1645.FANG Hai，ZHOU Quan.Multilevel reversible information hiding algorithm for multispectral images［J］.Journal of Computer Applications，2013，33(6):1622－1645.(in Chinese)

［13］MIGUEL A，RISKIN E，LADNER R，et al.Near－lossless and lossy compression of imaging spectrometer data:comparison of information extraction performance［J］.Signal，Image and Video Processing，2012，6(4):597－611.