无线传感器网络中DV－Hop 定位方法的一种改进策略*

石琴琴，周俊杰，张建平

(1.上海应用技术学院 计算机科学与信息工程学院，上海 201418;2.科大智能科技股份有限公司，上海 201203)

1 引言

DV－Hop(Distance Vector－ Hop)定位方法［1］是由美国路特葛斯大学(Rutgers University)的Dragos Niculescu 等人提出的一种非基于测距的定位方法，应用于无线传感器网络的节点自定位。其基本思想是借助网络中部分自身位置已知的节点(称为信标)，将未知节点到信标之间的距离用平均每跳距离和两者之间跳数的乘积表示，而后通过Lateration 算法计算未知节点的坐标。DV－Hop 方法不需要配备专门的距离测量设备，具有易于开展、可扩展性强、能量高效等优点，适用于分布式定位，且算法过程简单，已经成为一种经典的无线传感器网络节点定位方法，但是它在节点随机分布的网络环境下存在定位误差较大的问题，在满足实用需求层面仍然有很大的提高空间。

很多学者提出了多种基于经典DV－Hop 方法的改进策略，以期提高其在多样化应用环境下的定位精度。多数改进策略集中在DV－Hop 方法第1步中的平均跳距修正上面，如文献［2－4］中所列。这些策略在一定的实验环境下对定位误差有所改善，但针对各种可能出现的节点分布情况，未能从根本上解决节点间分布不均带来的估算误差。文献［5－6］中提出了针对DV－Hop 方法第2 步中使用的定位算法的改进策略，这些策略执行的计算条件均在默认距离估计值精确的前提下，且计算量较大，在分布式定位计算模型中使用存在很大挑战。

本文提出的改进策略主要的贡献在于:在距离估计阶段对每个未知节点，使用其1 跳内最近邻信标与其余各个信标的拓扑连接关系近似此未知节点与各信标之间的拓扑关系，独立确定未知节点与各信标间的平均跳距，以期使得估计距离尽量接近真实距离;在节点位置计算阶段，在使用Lateration 算法获得节点初始坐标后，将定位问题建模为使用牛顿迭代算法［7］求非线性方程组最优解的问题，实现进一步的位置求精计算，以期达到提高整体定位精度的目的。

2 DV－Hop 定位方法介绍

2.1 经典DV－Hop 方法

DV－Hop 定位方法采用基于多跳距离估计的节点自定位模型，其定位步骤可以概括为以下两步:

(1)使用典型的距离矢量交换协议，使网络中所有节点获得距离每个信标节点的最小跳数。每个信标节点在获得其他信标节点位置和相隔跳距之后，采用式(1)计算网络平均每跳距离，然后将其作为一个校正值广播至网络中:

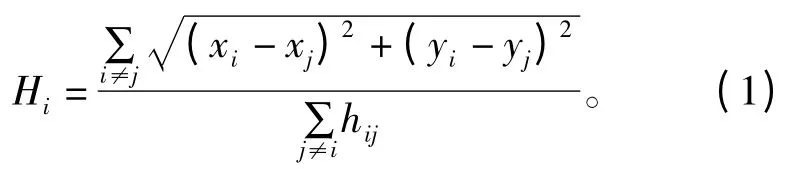
式中，(xi，yi)、(xj，yj)是信标节点i 和j 的坐标，hij是i 和j(i≠j)之间的跳段数。未知节点从最近的信标节点处接收校正值，依此估计自身到各信标节点之间的距离di，计算公式如式(2)所示:

式中，H 是网络平均跳距值的校正值，hi是未知节点到信标节点i 的最小跳数值;

(2)当某一未知节点获得与3 个或更多个信标节点之间的距离时，采用Lateration 算法实现定位计算。文献［8］对Lateration 算法的属性进行了研究与分析，结论为:Lateration 算法对测距误差敏感，而且当参与计算的信标节点数目大于4 时，再采用增加参与定位计算的信标数目并不能起到提高节点定位精度的作用，故本文实验采用4 个信标参与节点位置计算。

2.2 DV－Hop 方法既有改进策略分析

DV－Hop 方法的主要不足在于:当网络中的节点随机布设时，其分布的不均匀会使得通过全网信标节点间距离和与跳数和平均计算取得的每跳距离估值不能真实反映未知节点与每一个信标之间每跳平均距离值;另外，根据既有文献［8］对Lateration定位算法属性的研究，当距离误差较大时，其定位精度是不能保证的，因此，有必要增加求精步骤，以此提高整体的算法鲁棒性。

文献［2－3］在算法设计中忽略了RSSI 测距的不稳定性，做了精确测距的假设，平均每跳距离修正仍然采用全局的平均值对局部适用的参数进行修正;文献［4］可能出现阈值内信标数不足以实现定位的情况，并且增加了网络通信量和计算量。本文综合上述文献的优缺点，提出相应的改进策略，并命名为IDV－Hop(Improved DV－Hop)方法。

3 DV－Hop 方法改进策略

3.1 IDV－Hop 方法

IDV－Hop 方法相对于原方法具体的改进策略描述如下:

(1)在距离估计步骤中，针对每一个未知节点P，找出跳段距离最近的信标k，若其在1 跳范围内，则计算P 到其余信标i 的距离，采用的平均跳距为

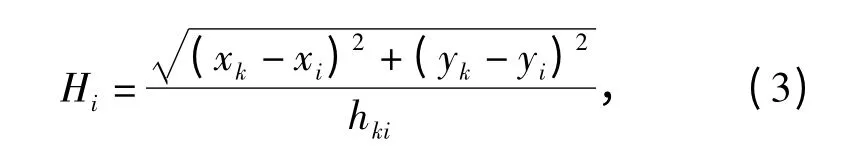
即采用当前未知节点最近的1 跳内信标与其他信标之间的多跳连接关系来近似未知节点与其他信标之间的多跳连接关系;若k 不在P 的一跳范围之内，则仍采用式(1)中的平均跳距;

(2)在节点位置计算阶段，根据文献［8］对信标选择的分析，选择跳距最近的4 个信标参与定位计算，使用Lateration 算法获得未知节点的初始坐标。而后，将定位问题建模为如式(4)所示的非线性方程组求最优解的问题:

方程组的待求未知数为未知节点的坐标x、y，以及未知节点与4 个信标之间的距离值d1、d2、d3、d4，使用牛顿迭代法求得方程组的解作为最终的节点定位值。

3.2 牛顿迭代法

本文通过实验对比了牛顿迭代法与最速下降法、共轭梯度法等其他常用的求解非线性方程组的方法在算法复杂度、收敛速度与收敛稳定性等方面的指标后，选择其中与Lateration 算法计算结果匹配度最好、收敛速度最快、收敛结果最稳定以及精度最高的牛顿迭代法作为初始定位结果的优化算法。牛顿迭代法的运算原理与方法步骤如下:

对式(4)中所列方程组，用fi(i=1，2，3，4)表示方程组中各等式左边未知数的函数表达式，用X(k)表示一组未知数x、y、d1、d2、d3、d4的当前值组成的列向量，在X(k)处按照多元函数的泰勒公式展开，并取线性项得到

由此得到的迭代公式为

对每一个未知节点，以IDV－Hop 方法在距离估计与位置计算两个步骤中获得的x、y、d1、d2、d3、d4的值组成初始值列向量X(0)，依照公式(7)展开迭代计算。

4 仿真实验

为评估本文改进策略的有效性，基于MATLAB7.0 对传统的DV－Hop 算法、文献［4］中的跳数加权改进算法及本文算法进行仿真实验，并对实验数据分析比较，对算法性能进行评价。本节首先描述仿真实验中的节点布设场景及仿真步骤，并介绍用于评价算法表现的参数，最后根据实验结果对所使用的算法及系统的整体表现进行详尽分析与评价。

4.1 实验环境

仿真实验环境参照文献［4］，节点部署在边长为100 单位的正方形区域内，为了取得更客观、更准确的实验数据，共设置两种实验场景:场景1 是在区域内随机生成100 个节点，改变其中信标节点的比例(10%～40%);场景2 是将信标节点个数固定为15，改变节点总数(100～400)。实验场景符合如下设定:网内所有节点都是同构的，且彼此之间无通信影响;所有节点具有相同的通信半径、相同的通信成功率及相同的路由协议，通信半径设置为20 单位，保证网络的连通性;文献［4］中跳数加权改进算法仿真时设定参与平均每跳距离参数估计的信标跳数阈值为原文献所述定位精度最高的值6。

在上述实验场景下仿真传统DV－Hop 方法、文献［4］中的跳数加权改进算法与本文所提改进策略IDV－Hop 的定位步骤。网络距离估计精度用所有未知节点与信标之间估计距离误差的平均值与标准差来衡量;定位精度用所有未知节点真实位置与定位计算获得的位置之间的距离，即点位误差的平均值及其标准差衡量。本文将误差归一化为节点通信半径的百分比进行表示。

4.2 实验结果与分析

实验场景1 模拟网络节点布设拓扑与信标比例变化，3 种算法的距离估计误差对比如图1 所示，距离估计误差标准差对比如图2 所示，定位误差对比如图3 所示，定位误差标准差对比如图4 所示。从图1 与图2 可知，3 种算法的距离估计误差都随着信标节点比例的增长而减小，本文改进算法可取得较低的距离估计误差，且当网内信标比例较低时，优势更为明显，并保持最低的距离估计误差标准差，因此可获得更稳定的距离估计精度。从图3 与图4 可知，3 种算法的定位误差都随着信标节点比例的增长而减小，且当信标比例超过25%时，减小的趋势趋于平缓，总体看来，本文算法对网络拓扑和信标比例变化的适应性最强，相对于原算法和文献［4］算法，定位精度平均提高约18%和10%，表现出较为平稳的定位误差与相对稳定的定位精度。

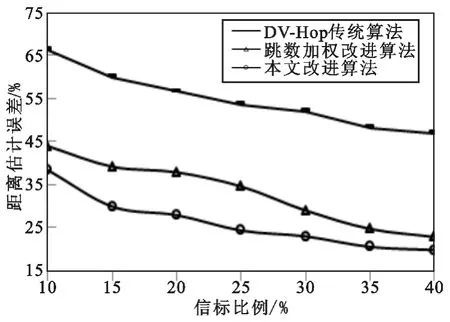
图1 距离估计误差与信标比例的关系Fig.1 Range error vs.beacon proportion

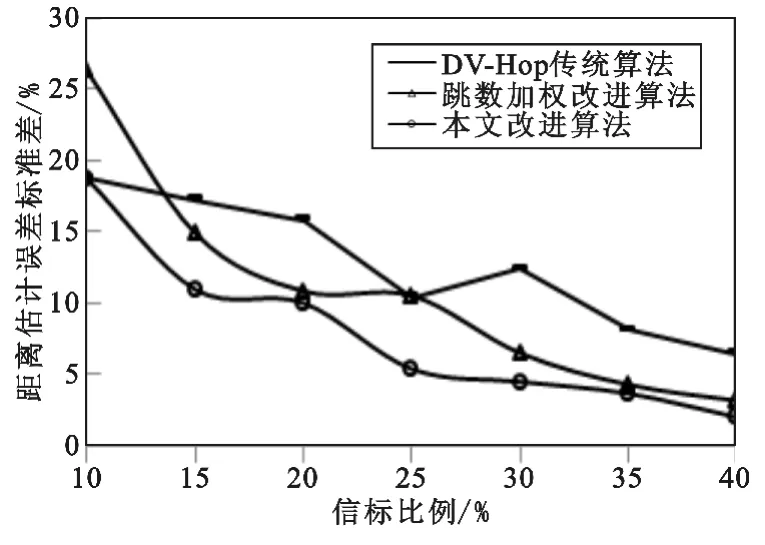
图2 距离估计误差标准差与信标比例的关系Fig.2 Range error standard deviation vs.beacon proportion

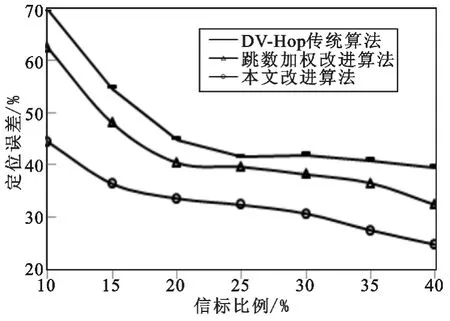
图3 定位误差与信标比例的关系Fig.3 Position error vs.beacon proportion

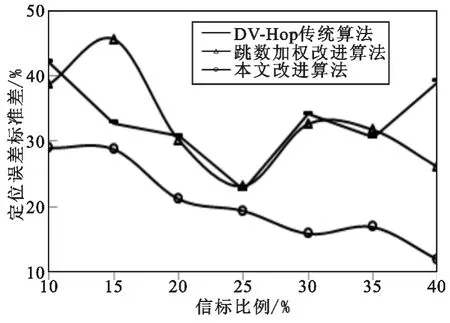
图4 定位误差标准差与信标比例的关系Fig.4 Position error standard deviation vs.beacon proportion

实验场景2 模拟网络节点布设拓扑与节点布设密度变化，3 种算法的距离估计误差对比如图5 所示，距离估计误差标准差对比如图6 所示，定位误差对比如图7 所示，定位误差标准差对比如图8 所示。从图5 与图6 可知，3 种算法的距离估计误差都随着节点布设密度的增长而减小，但整体变化趋势较平缓，本文改进算法与文献［4］算法相对原算法有较大改善，约为20%，两者之间的平均距离估计误差相差约4%，本文改进算法可取得较低的距离估计误差，并保持更稳定的距离估计精度。从图7 与图8 可知，3 种算法的定位误差都随着节点布设密度的增长而减小，总体看来，本文算法对网络节点布设密度的变化最为敏感，相对于原算法和文献［4］算法，定位精度平均提高约15%和10%，并可保持更稳定的定位精度。

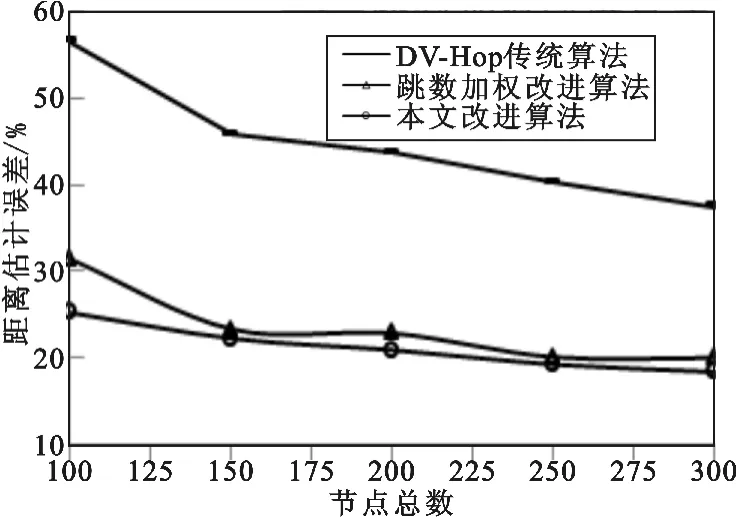
图5 距离估计误差与节点总数的关系Fig.5 Range error vs.number of nodes

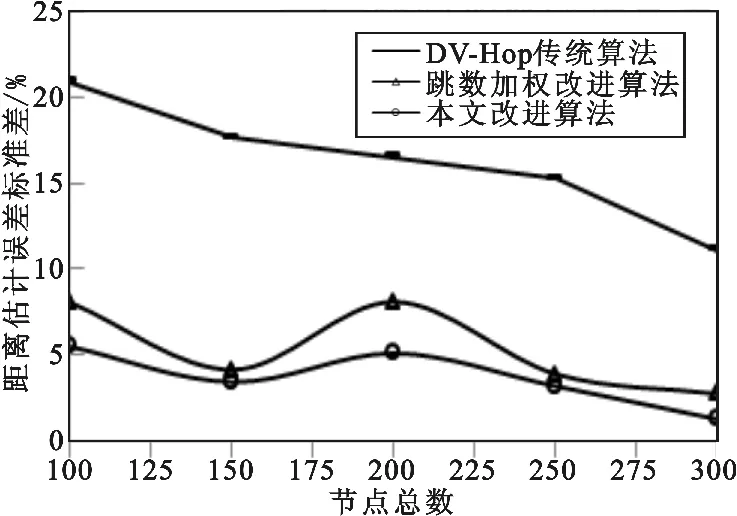
图6 距离估计误差标准差与节点总数的关系Fig.6 Range error standard deviation vs.number of nodes

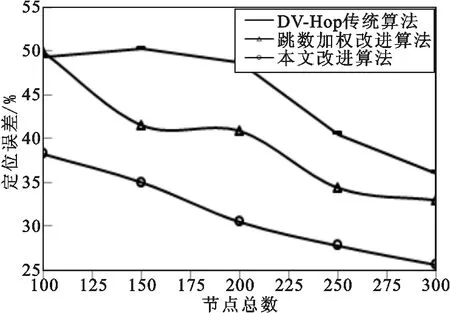
图7 定位误差与节点总数的关系Fig.7 Position error vs.number of nodes

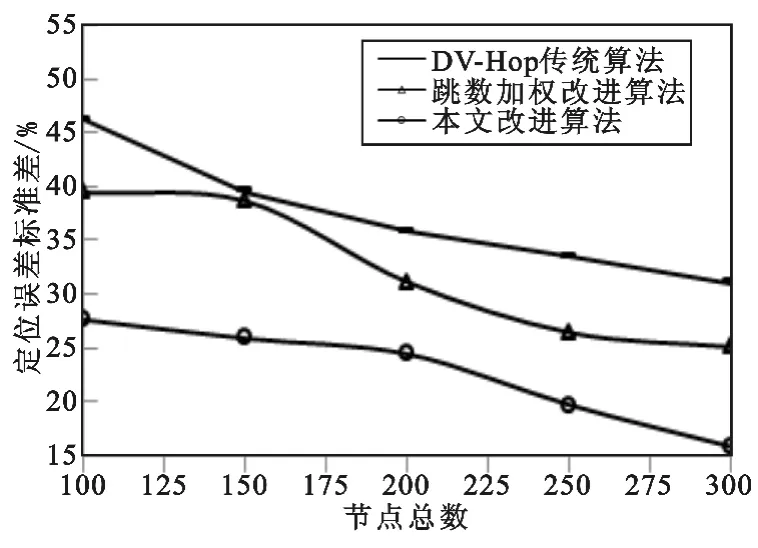
图8 定位误差标准差与节点总数的关系Fig.8 Position error vs.number of nodes

本文改进策略相对于原DV－Hop 方法未增加任何通信量，使用的牛顿迭代法对全部未知节点的计算都收敛，且平均迭代次数约为4 次，因此在不降低原DV－Hop 算法定位覆盖率的基础上以增加较小的计算量为代价可获得网络整体定位精度的提高。相对于文献［4］所述改进算法，本文改进策略节约了未知节点反算信标节点位置并广播误差修正值的计算量与通信量，且取得了较高且稳定的定位精度。

5 结束语

本文以经典DV－Hop 定位方法为研究对象，针对其在实际应用场景中存在的定位精度较低的问题进行算法改进。本文的改进策略不需要额外的硬件支持，也不需要额外的通信负荷来获得更多的计算条件。仿真实验表明:通过搜索最佳逼近路径，独立计算未知节点到每一信标节点的平均每跳距离，可有效提高网路的距离估计精度，从而获得提高节点定位精度的必要条件;在此基础上，为定位算法增加求精步骤，可提高算法对距离估计误差的鲁棒性，从而提高网络整体的定位精度。本文研究成果为在低造价、低能耗要求下解决无线传感器网络节点自定位问题提供了新的解决思路与方案，为无线传感器网络在多样化的应用环境下有效地实现节点自定位提供方法选择与策略指导，具有良好的实用价值与应用前景。

既有的研究工作主要针对DV－Hop 方法第2步所采用的定位算法进行了改进，本文改进策略则渐次对两个步骤的算法进行了改进，在研究层面进行了细化与综合。后续的研究将在搜索实际节点连接路径的最佳逼近策略与具体算法方面深入，以期提高测距精度，进一步增强方法的实用性。

［1］NICULESCU D，NATH B.DV based positioning in ad hoc networks［J］.Telecommunications Systems，2003，22(1):267－280.

［2］吴楠，刘方爱，王淑娴.基于跳数修正和跳距调整的DV－Hop 定位改进算法［J］.微电子学与计算机，2015，32(1):91－95.WU Nan，LIU Fangai，WANG Shuxian.Algorithm for locating nodes in WSN based on modifying hops and hopping distances［J］.Microelectronics ＆ Computer，2015，32(1):91－95.(in Chinese)

［3］夏少波，朱晓丽，邹建梅，等.基于跳数修正的DV－Hop 定位改进算法［J］.传感技术学报，2015，28(5):757－762.XIA Shaobo，ZHU Xiaoli，ZOU Jianmei，et al.The improved dv－hop algorithm based on hop count［J］.Chinese Journal of Sensors and Actuators，2015，28(5):757－762.(in Chinese)

［4］HU Y，LI X M.An improvement of DV－Hop localization algorithm for wireless sensor networks［J］.Telecommunication Systems，2013，53(1):13－18.

［5］李牧东，熊伟，梁青.基于人工蜂群改进算法的无线传感器网络定位算法［J］.传感技术学报，2013，26(2):241－245.LI Mudong，XIONG Wei，LIANG Qing.Wireless sensor networks node localization algorithm based on improved ABC algorithm［J］.Chinese Journal of Sensors and Actuators，2013，26(2):241－245.(in Chinese)

［6］ZHANG Y，XIANG S，FU W，et al.Improved normalized collinearity DV－ Hop algorithm for node localization in wireless sensor network［J］.International Journal of Distributed Sensor Networks，2014(2):1－14.

［7］张德丰.MATLAB 实用数值分析［M］.北京:清华大学出版社，2012:254－260.ZHANG Defeng.MATLAB numerical analysis and simulation examples［M］.Beijing:Tsinghua University Press，2012:254－260.(in Chinese)

［8］LANGENDOEN K，REIJERS N.Distributed localization in wireless sensor networks:a quantitative comparison［J］.Computer Networks，2003，43(4):499－518.