邻频干扰对跳频系统中断概率的影响*

刘广凯，全厚德，崔佩璋，胡晓玉，姚少林

(1.军械工程学院 信息工程系，石家庄 050003;2.大连理工大学 数学科学学院，辽宁 大连 116024)

1 引言

同一区域内布置的通信台站会产生互扰，如何根据系统的已知配置，分析互扰对系统性能的影响，是进行系统配置的主要考虑问题。国内外学者主要从接收端干扰信号的特征函数和联合概率密度函数分析接收端的信干噪比(Signal－to－Interference－and－Noise Ratio，SINR)，并给出中断概率、传输容量和误码率等性能指标。文献［1－2］假设干扰台站服从空间泊松分布，分别从信号层和能量层对干扰信号的特征函数进行分析，得到接收端干扰功率服从S(α，β，γ)偏正态分布的结论，并在Ad Hoc 网、分组交换网和其他通信系统中进行了应用［1，3－5］。文献［6］在文献［1－2］研究基础上，针对蜂窝通信系统，假定干扰台站在圆环区域内分布，得到中断概率的上、下限。文献［7－8］在信号层分析了同频干扰下干扰信号的特征函数。以上分析都假定系统内通信台站服从某一分布，从而得出相关结论，并未针对随意的确定位置进行分析。文献［9－12］从干扰信号的联合概率密度函数出发，分析了干扰台站在不同位置下，即位置固定、均匀分布和空间泊松分布，跳频系统受邻频干扰影响的中断概率和传输容量。文献［13］针对IEEE802.11a 系统搭建了邻频干扰实验平台，进行了相关分析和测试［13］。

跳频系统通过频表规划，有效减小了同频干扰，但考虑到用频效率，仍会存在一定程度的邻频干扰。本文以跳频通信中的某一通信频点，针对邻频干扰对跳频系统中断概率的影响，在已知干扰台站布置的条件下，通过分析接收端SINR 的分布函数，得到以信道参数、干扰台站数和可用频点数为变量的中断概率公式，并进行仿真验证。

2 系统模型

2.1 系统布置

美国陆军超短波跳频系统的典型应用场景如图1 所示，接收方R0周围散布着其他通信台站i={1，2，…，M}，M 表示区域内干扰台站总数。接收方接收远端的发送信号时，会受到周围台站发射信号的邻频干扰。

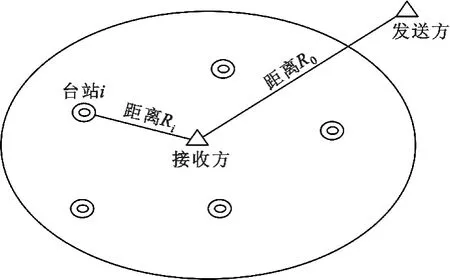
图1 系统配置Fig.1 System configuration

以接收方所在位置为原点，建立极坐标系，R0为通信距离，Ri为第i 个干扰台站与接收方距离，通信过程中，各台站保持位置固定。信号功率为P0，干扰台站i 发射频谱的邻频功率为Pi，i={1，2，…，M }。分配给整个区域的可用频点数为F，则邻频干扰概率［11］为

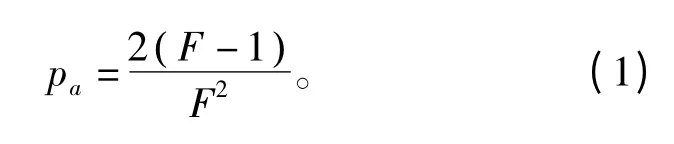
考虑到频表规划带来的邻频干扰概率增益，式(1)可写为

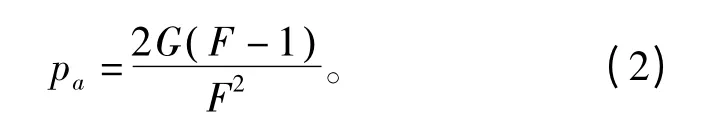
式中，G 表示频表规划带来的邻频干扰概率增益。

2.2 信道模型

信道的作用集中表现为路径损耗、阴影衰落和小尺度衰落，经过信道作用后，台站i 到达接收端的功率为

式中，n 为路径损耗指数，一般在3～8 之间;εi～N (0，σ)为第i 条信道的阴影衰落因子;gi=，且E [ gi]=1，αi为小尺度衰落因子。

由于αi服从Nakagami－ m 分布，则gi服从分布［1］，且其概率密度函数为

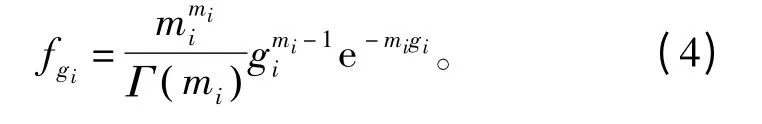
式中，mi为第i 条信道的Nakagami 参数，假定其在一个符号周期内不变。

2.3 接收端信干噪比

接收端信干噪比为信号功率与噪声、干扰功率之比，可表示为

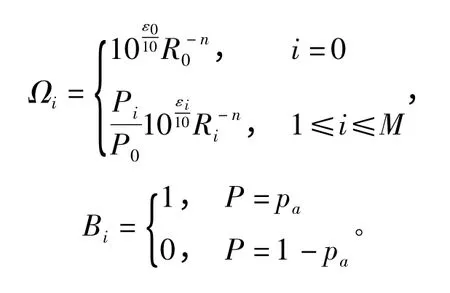
3 系统中断概率

通信系统中的中断概率定义为接收端SINR 低于某一中断门限的概率，可表示为

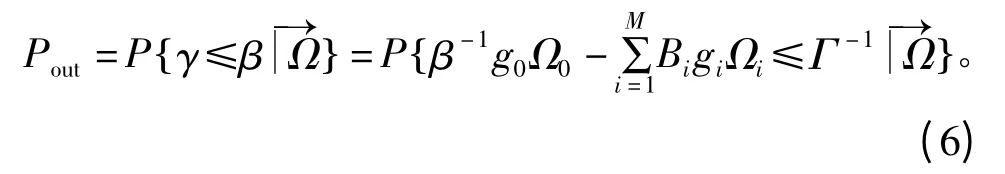
令

则式(6)可写为

式中，fs(s) 为接收端信号功率的概率密度函数，为接收端干扰功率的联合概率密度函数。

由式(4)可得s 的概率密度函数为

根据定积分公式

可得s 的定积分

令β0=，将式(10)代入式(7)得

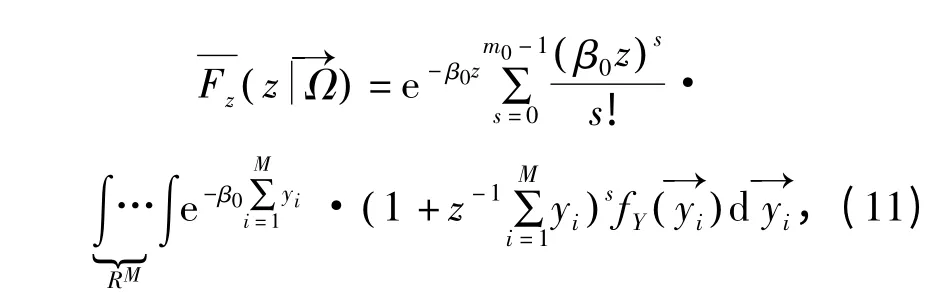
且s={0，1，…，m0－1 }为正整数，根据二项式定理，可得

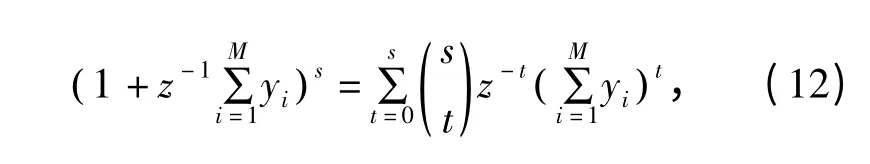
根据多项式定理，可得

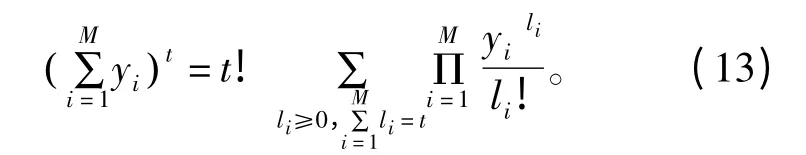
将式(12)和式(13)代入式(11)，得

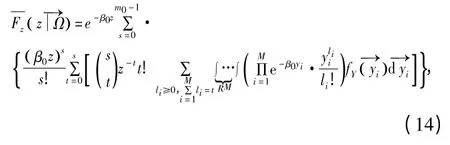
且每条干扰台站与接收方的信道相互独立，即

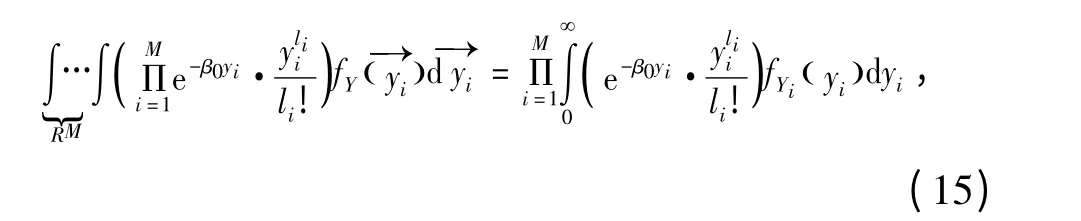
则式(14)可化简为

与式(8)类似，可得yi的概率密度为

将式(17)代入式(15)，得

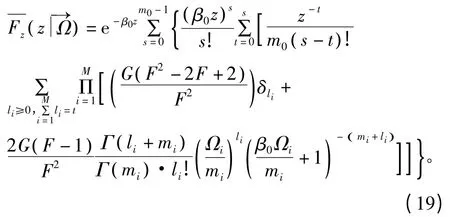
式中，mi，i={0，1，…M }为对应的信道参数，M 为干扰台站数，F 为可用频点数，G 为邻频干扰概率增益，其他参数为中间变量。

4 仿真结果

为验证所提中断概率公式的正确性，以美陆军超短波频段中55 MHz的频点为例，针对不同的Nakagami 信道参数、台站数量和可用频点数，对系统中断概率进行仿真。首先，给出3 个实验的仿真参数:噪声功率N=－30 dBm，干扰台站发射频谱的邻频功率Pi=－20 dBm，i={1，2，…，M}，信噪比在－5～25 dB之间变化，通信双方相距10 km，干扰台站在2～8 km之间均匀分布，邻频干扰概率增益G=1，中断门限β=0 dB，仿真实验进行100 000次。实验结果如图2～4 所示。

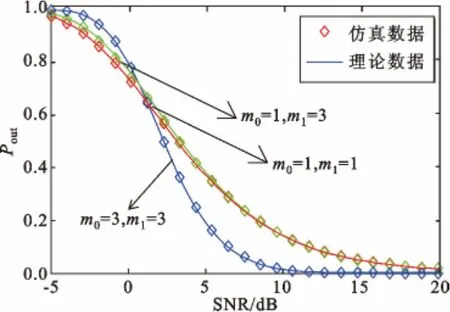
图2 pa=1、M=4 时，Pout与SNR 关系Fig.2 The relationship between Poutand SNR when pa=1，M=4

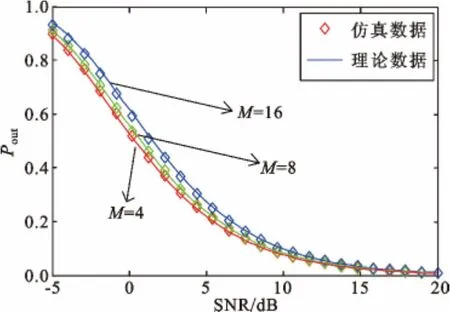
图3 F=10、m0=1、mi=3 时，Pout与SNR 关系Fig.3 The relationship between Poutand SNR when F=10，m0=1，mi=3

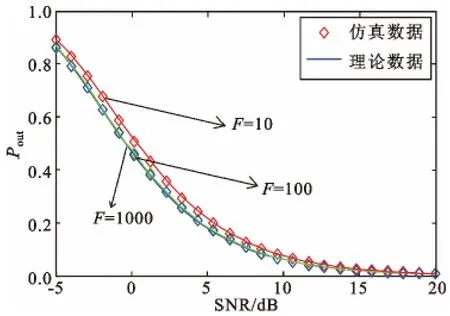
图4 M=4、m0=1、mi=3 时，Pout与SNR 关系Fig.4 The relationship between Poutand SNR when M=4，m0=1，mi=3

根据Nakagami 信道参数m 与Rice 因子K 的关系［14］可得出m 在一定程度上代表直射路径的能量，即Rayleigh 信道中K0=0，Ki=0，i={1，2，…，M}，混合信道中K0=0，Ki=4.5，i={1，2，…，M}和Nakagami 信道中K0=4.5，Ki=4.5，i={1，2，…，M}。从图2 中可以看出:当SNR 较小时，对比混合信道与Rayleigh 信道，前者会因为干扰信道存在直射能量，中断概率比Rayleigh 信道大;当SNR 较大时，对比混合信道与Nakagami 信道，前者会因为通信信道不存在直射能量，中断概率会比Nakagami 信道大;但随着SNR 的升高，台站干扰不再是主要因素，3 种信道的中断概率会都趋于0。

在实验3 和4 中，为了分析方便和实验简单，将4 个干扰信道的信道状态设为相同，即均为混合信道条件。

从图3 中可以看出:在信道参数和可用频点数一定的条件下，当SNR 较小时，干扰能量是主要的影响因素，干扰台站数越大，中断概率越大;但随着SNR 的增大，台站干扰不再是主要因素，三者的中断概率会都趋于0。

从图4 中可以看出:在信道状态和干扰台站数一定的条件下，根据可用频点数与干扰概率的关系，随着可用频点数增多，中断概率变小;但可用频点数与邻频干扰概率是类反比关系，随着可用频点数的增多，邻频干扰概率降低的效果会越来越差，导致中断概率变化不大。

5 结束语

本文针对邻频干扰对跳频系统中断概率的影响，在干扰台站布置已知的情况下，得到了系统中断概率的表达式，并针对系统的重要参数(信道参数、干扰台站数和可用频点数)进行了理论计算和仿真验证，证明了理论的正确性。理论和仿真结果表明:对于跳频系统而言，信道参数是影响中断概率的最重要因素，其次是干扰台站数;而对于减小中断概率而言，增大可用频点数并不是一个好的方案。本文从跳频通信中的某一通信频点出发，通过假设该频点处的邻频干扰功率大小，进行了中断概率的分析，但不同的载波频率对邻频干扰功率的大小可能会有影响，定量化的影响效果是下一步的研究内容。本文得出的理论公式为跳频系统的性能分析和不同信道条件下的台站布置提供了指导。

［1］WIN M Z，PINTO P C，SHEPP L A.A Mathematical Theory Of Network Interference and Its Applications［J］.Proceedings of the IEEE，2009，97(2):205－230.

［2］PINTO P C，WIN M Z.A Unified Analysis of Connectivity and Throughput in Packet Radio Networks［C］//Proceedings of 2008 Military Communications Conference.San Diego，CA:IEEE，2008:1－7.

［3］PINTO P C，WIN M Z.Communication in a Poisson Field of Interferers——Part I:Interference Distribution and Error Probability［J］.IEEE Transactions on Wireless Communications，2010，9(7):2176－2186.

［4］PINTO P C，WIN M Z.Communication in a Poisson Field of Interferers——Part II:Channel Capacity and Interference Spectrum［J］.IEEE Transactions on Wireless Communications，2010，9(7):2187－2195.

［5］CARDIERI P.Modeling Interference in Wireless Ad Hoc Networks［J］.IEEE Communications Surveys ＆ Tutorials，2010，12(4):551－572.

［6］ZHANG T，AN L，CHEN Y，et al.Aggregate Interference Statistical Modeling and User Outage Analysis of Heterogeneous Cellular Networks［C］//Proceedings of 2014 IEEE International Conference on Communications.Sydney:IEEE，2014:1260－1265.

［7］GULATI K，CHOPRA A，EVANS B L，et al.Statistical Modeling of Co－Channel Interference［C］//Proceedings of 2009 IEEE Global Telecommunications Conference.Honolulu，HI:IEEE，2009:1－6.

［8］GULATI K，EVANS B L，TINSLEY K R.Statistical Modeling of Co－ Channel Interference in a Field of Poisson Distributed Interferers［C］//Proceedings of 2010 IEEE International Conference on Acoustics Speech and Signal Processing.Dallas，TX:IEEE，2010:3490－3493.

［9］TORRIERI D，VALENTI M C.The Outage Probability of a Finite Ad Hoc Network in Nakagami Fading［J］.IEEE Transactions on Communications，2012，60(11):3509－3518.

［10］VALENTI M C，TORRIERI D，TALARICO S.A Direct Approach to Computing Spatially Averaged Outage Probability［J］.IEEE Communications Letters，2014，18(7):1103－1106.

［11］VALENTI M C，TORRIERI D，TALARICO S.Adjacent－Channel Interference in Frequency－Hopping Ad Hoc Networks［C］//Proceedings of 2013 IEEE International Conference on Communications.Budapest:IEEE，2013:5583－5588.

［12］VALENTI M C，TORRIERI D，TALARICO S.Optimization of a Finite Frequency－hopping Ad Hoc Network in Nakagami Fading［C］//Proceedings of 2012 Military Communications Conference.Orlando，FL:IEEE，2012:1－6.

［13］ANGELAKIS V，PAPADAKIS S，SIRIS V，et al.Adjacent－Channel Interference in 802.11a:Modeling and Tested Validation［C］//Proceedings of 2008 IEEE Radio and Wireless Symposium.Orlando，FL:IEEE，2008:591－594.

［14］FOTOHABADY V，SAID F.Comparison of the Rayleigh and Nakagami Fading Channels MIMO Multicarrier System［C］//Proceedings of 2011 Wireless Advanced(WiAd).London:IEEE，2011:295－300.