基于加权最小二乘支持向量机的欠定盲源分离*

赵立权，刘珊珊

(东北电力大学 信息工程学院，吉林 吉林 132012)

1 引言

盲源分离是指在信源信号以及传输信道参数均未知的情况下，仅通过对观测信号进行处理实现信源信号的估计。由于其打破了传统信号处理的特点，因此成为当今信号处理领域研究的热点之一，并且在通信信号、语音识别、图像处理、医学信号处理、故障诊断等方面得到了广泛的应用［1－3］。盲源分离技术在实际应用中经常会出现信源信号个数大于传感器个数的情况，即欠定的情况。针对该问题，2001年学者们提出了欠定条件下的盲源分离，即欠定盲源分离［4］。

欠定盲源分离是指在信源信号和信道参数未知且观测信号个数小于信源信号个数的条件下，从观测信号中恢复出信源信号的信号处理方法。欠定盲源分离过程主要分两步:第一步估计出混合矩阵，第二步根据估计出的混合矩阵采用线性规划等方法估计出信源信号。目前，欠定盲源分离的研究主要集中在对混合矩阵估计方法的研究和对混合矩阵估计后信源信号恢复方法的研究。本文主要研究混合矩阵的估计方法。

目前，混合矩阵估计的估计方法主要有基于态势函数方法［4－5］、K－均值聚类算法［6－7］、基于张量分解方法［8］、基于支持向量机的方法［9］、基于模糊C均值聚类方法［10］、基于层次聚类方法［11］等。基于态势函数的方法仅适用于观测信号个数为2 的欠定系统，适用范围受限;基于张量分解的方法系统较为复杂，计算量较大;基于聚类分析的混合矩阵估计方法的性能受聚类中心的选择影响较大;基于支持向量机的方法克服了上述问题，但是支持向量机模型较为复杂，对抗奇异点性能较差。加权最小二乘支持向量机(Weighted Least Square Support Vector Machine，WLS－SVM)［12］相对支持向量机性能更好，因此，为了进一步提高基于支持向量机的欠定盲源分离方法［9］的性能，本文提出了基于加权最小二乘支持向量机的欠定盲源混合矩阵估计方法。

2 欠定盲源分离

欠定盲源分离数学模型可以描述为［4］

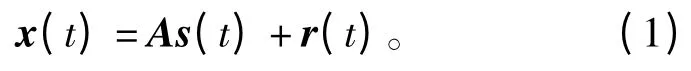
式中，s(t)=［s1(t)，s2(t)，…，sn(t)］T表示源信号在时刻t 的向量;x(t)=［x1(t)，x2(t)，…，xm(t)］T表示t 时刻的m 维观测向量;r(t)为噪声信号;A=(aij)为m×n 的混合矩阵(m ＜n)。

假设观测到的语音信号个数为2，信源信号稀疏，且忽略噪声的影响，则二元欠定盲源分离模型可以表示为

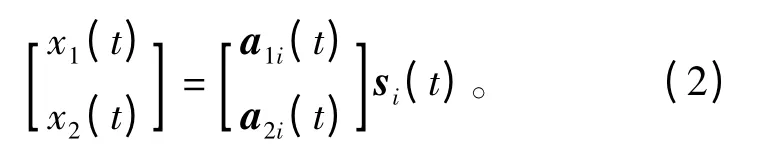
式中，x(t)为观测信号，a(t)为混合矩阵，si(t)为第i 个信源信号。由于假设si(t)具有一定的稀疏性，且观测信号经过稀疏化，因此混合矩阵在t 时刻仅存在混合矩阵其中的一列。在极坐标中，t 时刻观测信号的夹角(方向角度)为

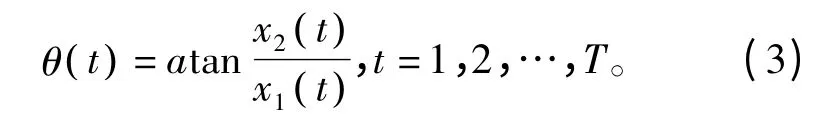
根据式(3)得到的所有时刻点的方向角度进行等距离分类，分类的数目尽量大于观测信号在极坐标图中信号角度较集中的(某方向上的密集点数约为总点数的1/4)方向个数。将某个区间包含的信号点数与总信号点数的比值设为置信度，即若区间包含的样本数为Mi，此区间的置信度可表示为

式中，T 代表总的采样点数，Di为对应区间的置信度。根据置信度的不同确定源信号数目，从而确定混合矩阵的列数。

3 加权最小二乘支持向量机

加权最小二乘支持向量机是在LS－SVM 的基础上给误差变量加一权值，从而得到更优的分类函数。假设给定的输入空间的训练样本为

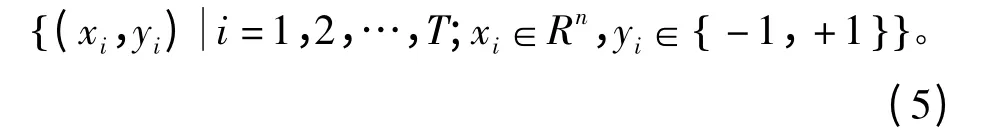
式中，xi为样本点在某空间的坐标，yi为样本点所属的类别。对此类样本进行分类，则WLS－SVM 的函数估计问题可表示为［12］

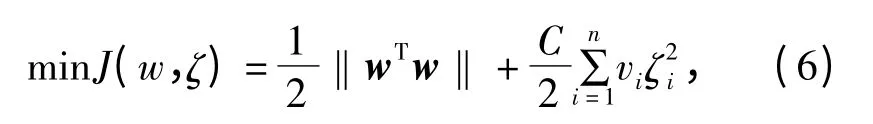
约束条件为

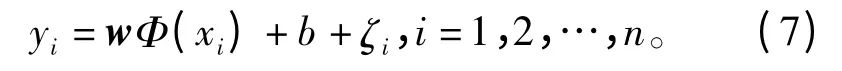
式中，C 为正则化参数，ζi为样本的误差变化量，vi为误差的加权系数，b 为最近点距分类平面的距离。将模型变换后得到的拉格朗日函数为

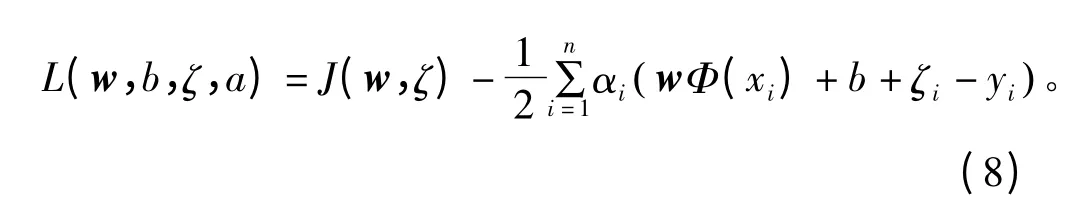
对式(8)中的参数求偏导并消除w 和ζ。得到新的KKT(Karush－Kuhn－Tucker)系统函数为

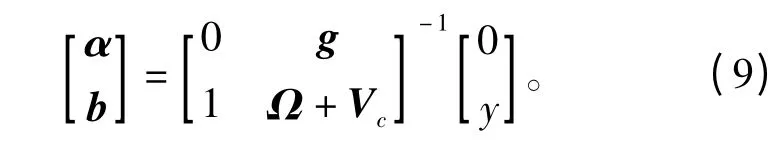
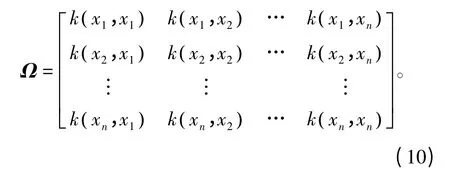
权值vi的大小通过式(11)确定:

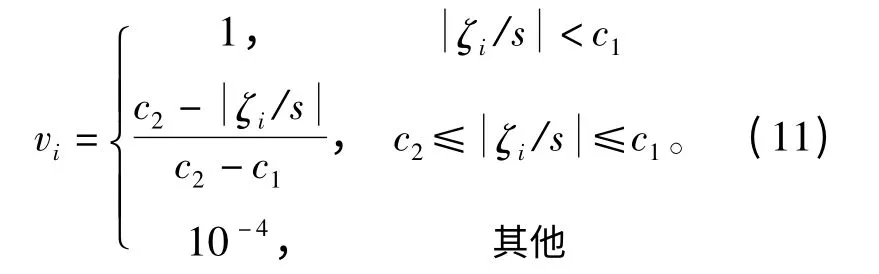
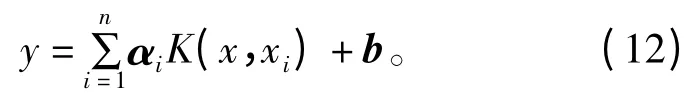
式中，K (x，xi)采用高斯径向基核函数。

4 改进的欠定盲源分离

为了提高基于支持向量机的欠定盲源分离算法的性能，本文采用WLS－SVM 对欠定盲源分离中的混合信号进行分类，提高算法的精度。由式(9)，根据加权最小二乘算法确定拉格朗日因子及平面所有点距平面的最短距离b。加权因子的大小是根据对应样本的误差值确定的，误差越大对应的加权因子就越小，为此本文对利用WLS－SVM 方法得到的加权系数进行逐一更新。首先根据加权系数的排列顺序，从大到小每次将一个样本点作为测试样本，对其余的样本点按式(13)进行计算，根据计算结果更新测试样本的误差值，再根据式(11)计算相应的权值，从而实现误差变量及加权系数的更新。

设定正则化参数和所有点的加权系数。将样本xj(j=1，2，…，n)作为检验样本，剩下的 (n－1)个样本作为训练样本，此时的求解方程变为

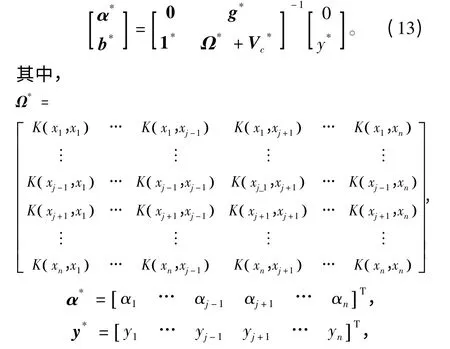
矩阵g 和I 也会去掉相应的第j 行变为g*和I*。此时第j 个样本的残差值为=j*·α*+b*，j*为矩阵的第j 行向量。用代替原来的yj，再采用式(11)对相应的加权系数进行更新，之后进行下一个样本的更新计算。

改进的欠定盲源分离算法具体实现步骤如下:

(1)首先将得到的观测信号通过窗函数及快速傅里叶变换(Fast Fourier Transform，FFT)进行稀疏化处理，使其具有明显的稀疏性，再对样值进行标准化处理，使其均值为零，方差为1，记为 x (t)，t=1，2，…，T;

(2)本文根据观测信号采样点在极坐标图中密集度的不同，将所有采样点进行初步分类，通过至少T 次试验确定包含点数最多的前m 个(一般Di≥0.2)区间为相对最优置信区间，此时信源的数目也可以确定为m。对于剩下的非最优置信区间，根据置信度的值将样本点很少且其角度与选取的最优置信区间的角度相差很大的区间去掉，既可以减小计算量，又可以减小误差。将剩下点定义为x1(t)，t=1，2，…，T;

(3)将最优置信区间的样本点作为训练样本，其余的为测试样本，采用最小二乘算法得到样本误值，运用WLS－SVM 得到相应样本的加权因子;

(4)采用公式(13)进行权值的更新，确定最优分类平面，从而进行测试样本的分类;假设分类平面的法向量为Wi，最近点距最优平面的距离为b，将x1(t)中的所有点进行分类，可依据式(14)划分:

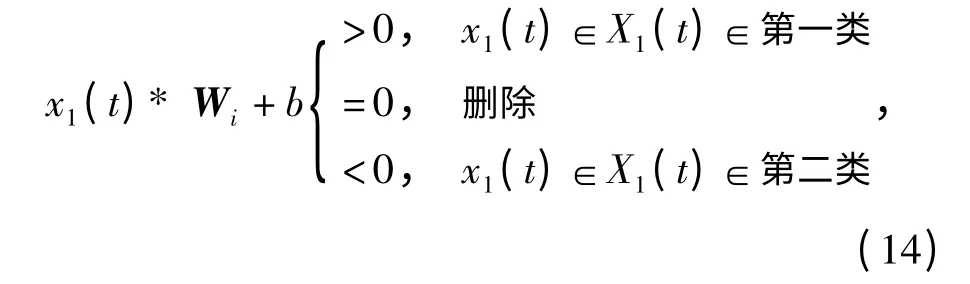
再以同样的方法将上述中的(m－1)类取出一类与剩余的所有类进行划分，得到平面的法向量Wj，再将上次分类中属于第一类的信号点进行分类，多次运用支持向量机依次实现所有信号点的进一步分类;

(5)为了更精确地估计出混合矩阵，再将每类样本(Pi)按角度分为若干类，并计算每类新样本的置信度(Pij)及每个新样本的均值 (Peij)为一列向量，将两者进行加权，即可得到对应的混合矩阵的某一列向量，从而估计出整个混合矩阵。

5 仿真实验

为验证上述方法的有效性，本文采用3 路具有一定稀疏性的语音信号作为信源信号，采用MATLAB 工具通过对混合信号分类实现混合矩阵的估计。设其混合矩阵为

图1 是信源信号，图2 是经过混合矩阵得到的混合信号。采用傅里叶变换方法将语音信号变换到频域，用加窗的方法，即在频域波形中用以一定时间长度为宽度的窗函数进行平移，去掉频域中重叠的信号部分，获得频域的离散图。为了更精确地对不同时刻的信号进行区分，再将离散图中信号点频谱很集中的部分去掉，保留频谱变化较大的信号点，从而实现信号的稀疏化。

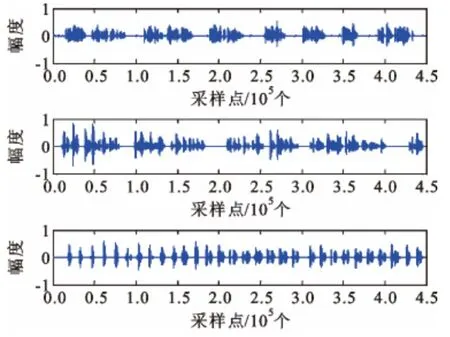
图1 信源信号Fig.1 Source signals

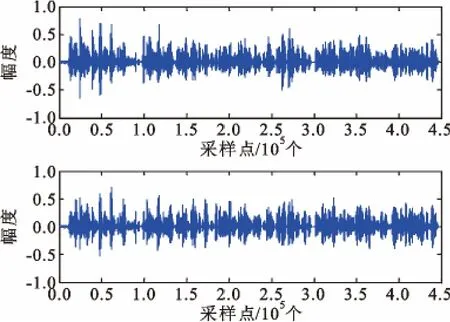
图2 经过混合矩阵得到的混合信号Fig.2 Mixed signals by mixed matrix

为说明本文算法的有效性，在相同条件下本文算法得到的混合矩阵为

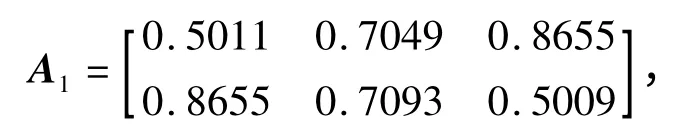
采用K－均值方法［6］得到的混合矩阵为

采用SVM 方法［9］得到的混合矩阵为

对不同算法估计得到的矩阵，通过对比原矩阵与估计矩阵的相应列的角度差值来衡量估计矩阵的偏差，相应列的夹角表示为

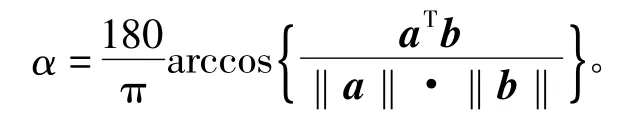
式中，a 和b 为同维数的列向量。夹角差越小意味着估计矩阵与原矩阵对应列之间的误差越小，两者越接近，当两者完全相等的时候，夹角差为0，所以夹角差越小误差越小。

表1 中的每列是相应算法估计的矩阵与原矩阵每列的角度偏差值，该差值是算法运行100 次得到的平均值。从表1 中可以看出本文算法的角度误差更小，证明本文算法具有更小的误差。

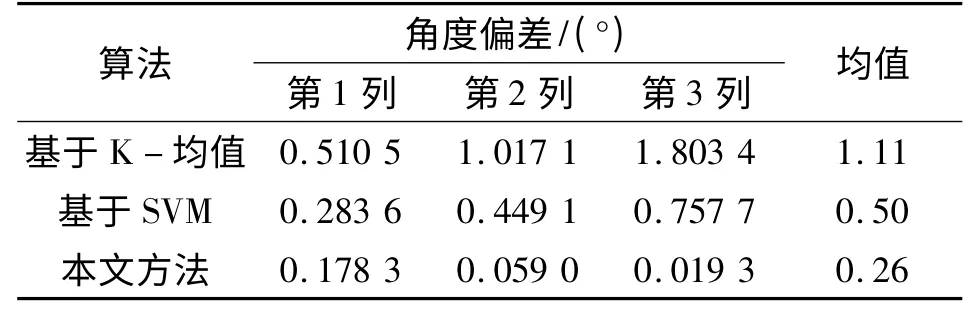
表1 估计矩阵与原矩阵对应列角度偏差的对比(图1 信源信号)Table 1 Angular difference between estimated and original matrix(source signals in Fig.1)

为了进一步验证本文提出的算法对真实语音信号的有效性，本实验采用TIMIT 语音数据库中的语音信号作为信源信号(图3)，采样速率为8 kHz，图4为混合信号，图5 为采用本文方法估计出混合矩阵后，采用最短距离方法恢复出来的信号。通过对图3 信源信号和图5 分离信号的数据的读取，可以听出分离信号的语音和信源信号的语音是一致的，分别是Her wardrobe consists…、Elderly people are…、Put the butcher…、Pizzerias are convenient，而且两个图的波形也基本一样，证明了算法的有效性。

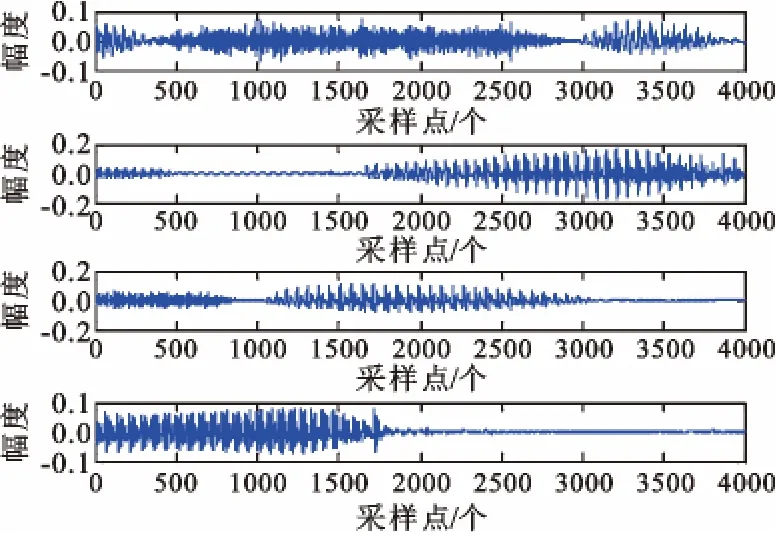
图3 信源信号(TIMIT 语音数据库中的语音信号)Fig.3 Source signals from TIMIT voice database

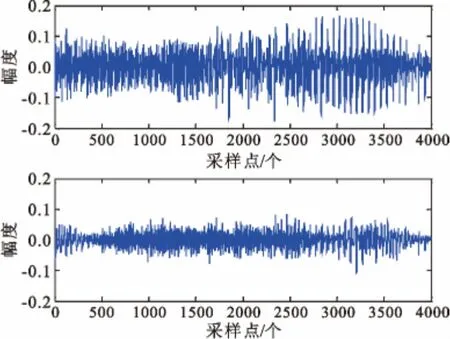
图4 混合信号Fig.4 Mixed signals

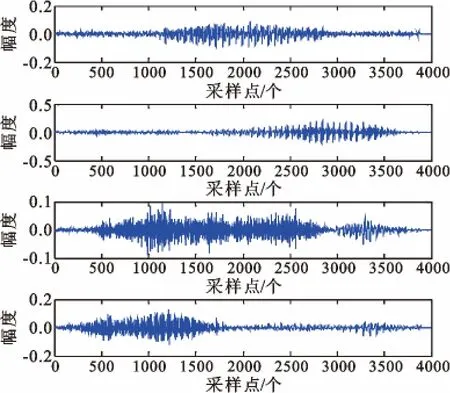
图5 分离信号Fig.5 Separated signals

表2 中的每列是相应算法估计的矩阵与原矩阵每列的角度偏差值，该差值是算法运行100 次得到的平均值。从表2 中可以看出本文算法的角度误差更小，证明本文算法具有更小的误差。

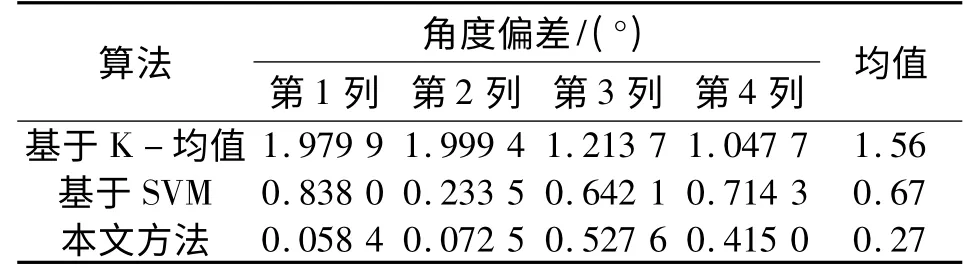
表2 估计矩阵与原矩阵对应列角度偏差的对比(图3 信源信号)Table 2 Angular difference between estimated and original matrix(source signals in Fig.3)

6 结束语

本文针对欠定盲源分离中混合矩阵的估计问题，提出利用信号角度偏差进行基本分类，再以加权最小二乘支持向量机法为基础，根据误差值的变化逐步的对加权系数进行更新，从而获得最优的分类平面。通过恢复矩阵与原矩阵的角度偏差对比证明本文算法提高了混合矩阵估计准确度。本文算法的平均误差是基于K－均值方法误差的0.2 倍左右，是基于SVM 算法平均误差的0.5 倍左右。下一步将引入蚁群优化算法对支持向量机的参数进行参数优化，进一步提高分类精度。

［1］NAIK G R，KUMAR D K.An Overview of Independent Component Analysis and Its Applications［J］.Informatica，2011，35(1):63－81.

［2］董江山，李成范，赵俊娟，等.基于变分贝叶斯ICA 的遥感图像混合像元分析［J］.电讯技术，2013，53(10):1274－1277.DONG Jiangshan，LI Chengfan，ZHAO Junjuan，et al.Mixed Pixel Analysis of Remote Sensing Image Based on Variational Bayesian ICA Method［J］.Telecommunication Engineering，2013，53(10):1274－1277.(in Chinese)

［3］穆昌，姚俊良.一种改进的基于多用户检测的独立分量分析算法［J］.电讯技术，2014，54(6):791－795.MU Chang，YAO Junliang.An Improved Independent Component Analysis Algorithm Based on Multiuser Detection［J］.Telecommunication Engineering，2014，54(6):791－795.(in Chinese)

［4］BOFILL P，ZIBU L M.Underdetermined blind source separation using sparse representations［J］.Signal Processing，2001，81(11):2353－2362.

［5］李丽娜，曾庆勋，甘晓晔，等.基于态势函数与压缩感知的欠定盲源分离［J］.计算机应用，2014，34(3):658－662.LI Lina，ZENG Qingxun，GAN Xiaoye，et al.Under－determined blind source separation based on potential function and compressive sensing［J］.Journal of Computer Application，2014，34(3):658－662.(in Chinese)

［6］LI Y Q，CICHOCKI A，AMARI S.Analysis of sparse representation and blind source separation［J］.Neural Computation，2004，16(6):1193－1234.

［7］毕晓君，宫汝江.基于混合聚类和网格密度的欠定盲矩阵估计［J］.系统工程与电子技术，2012，34(3):614－618.BI Xiaojun，GONG Rujiang.Undetermined blind mixing matrix estimation algorithm based on mixing clustering and mesh density［J］.System Engineering and Electronics，2012，34(3):614－618.(in Chinese)

［8］张延良，楼顺天，张伟涛.欠定盲源分离混合矩阵估计的张量分解方法［J］.系统工程与电子技术，2011，33(8):1073－1076.ZHANG Yanliang，LOU Shuntian，ZHANG Weitao.Estimation of undetermined mixture matrix in blind source separation based on tensor decomposition［J］.System Engineering and Electronics，2011，33(8):1073－1076.(in Chinese)

［9］李荣华，杨祖元，赵敏，等.基于支持向量机的欠定盲源分离［J］.电子与信息学报，2009，31(2):320－322.LI Ronghua，YANG Zuyuan，ZHAO Min，et al.SVM based Undetermined blind source separation［J］.Journal of Electronics ＆ Information Technology，2009，31(2):320－322.(in Chinese)

［10］ALSHABRAWY O S，AWAD W，HASSANIEN A E.Underdetermined blind source separation based on fuzzy C－ means and semi－ nonnegative matrix factorization［C］//Proceedings of 2012 Federated Conference on Computer Science and Information Systems.Worclaw，Poland:IEEE，2012:659－700.

［11］MOURAD N，REILLY J.Modified hierarchical clustering for sparse component analysis［C］//Proceedings of ICASSP2010.Dallas，TX:IEEE，2010:2674－2677.

［12］WEN W，HAO Z.A Heuristic weight－stetting strategy and iteratively updating algorithm for weighted least squares support vector regression［J］.Neurocomputing，2008，71(16－18):3096－3013.