基于稀疏分解和混沌理论的微弱信号检测*

徐一红，祝长生，赵耀培

(1.山东管理学院 机电学院，济南 250100;2.山东科技大学 机电工程系，山东 青岛 266590)

1 引言

微弱信号检测广泛应用于通信、医学、导航和电子技术等领域，并且在信号处理方面一直是研究的热点和难点。锁定放大器(Lock－In Amplifier)作为微弱信号检测领域的一种有效方法，能够很好地解决噪声干扰问题。国内外早期进行的研究主要针对模拟型锁定放大器，但这种放大器通常会受到来自模拟器件的限制，造成在积分上时间较短、频率相同等不容易克服的困难［1］。数字式锁定放大器相对于模拟锁定放大器来说，克服了许多缺陷，在功能上有了一定的提升:可灵活定制，处理能力强，数据吞吐率大。数字式锁定放大器已成为锁定放大器的主流［2］。

在不同类型的锁定放大器层出不穷的背景下，许多国内外研究人员也研究了不同的算法用于微弱信号的锁定。赵玲等［2］实现了频率自动跟踪的数字锁定放大器，数字锁定放大器的处理信号能力逐步加强;王坤朋等［3］采用盲源分离算法将信号与噪声分离;蒋世文等［4］用稀疏分解算法进行信号检测;刘寅等［5］用空间谱估计算法进行了研究，提出一种利用信号子空间信息的ESPRIT 匹配追踪算法。在现有的研究中，在微弱信号检测算法运用到数字锁定放大器时，主要存在运算复杂度过高、频率检测精度不高的问题［6－7］。本文研究内容主要集中在优化频率搜索算法的基础上，提高信号检测的频率精度。非线性(Non－Linear，NL)科学快速发展，李月等［8－9］用混沌振子对微弱周期信号敏感的特性，将其运用到微弱信号检测。胥小波等［10］用混沌振子改进了粒子群算法，提高了检测搜索的效率。由于非线性检测的原理机制完全不同于传统的信号检测方法，如今的通信设备所存在的弊端利用非线性系统可能迎刃而解。所以基于非线性方法的复杂调制信号的信号检测技术急需实现，弥补现有通信传输技术的不足。本文将非线性方法应用到数字锁定放大器中，进一步提升数字锁定放大器的性能。

2 数字锁定放大器的整体设计

数字锁定放大器主要由信号通道、参考通道、相敏检测器和低通滤波器四部分组成，其原理如图1所示。

图1 锁定放大器原理图Fig.1 The principle diagram of the lock－in amplifier

锁定放大器利用参考输入信号与有用信号存在相关性，从而进行相干检测，其中互相关运算是通过其内部结构中的相干检测和低通滤波来实现，输入信号中的噪声部分与参考信号互不相关而得到抑制。

数字锁定放大器在搜索信号过程中采用了稀疏分解算法，实现了信号的自动捕获。根据稀疏分解算法的思想，在参考信号部分建立了原子库。由于正弦函数信号相位偏移不可预测，正交双路放大器避免相位因素的干扰，式(1)、式(2)表示正余弦双原子的数学模型:

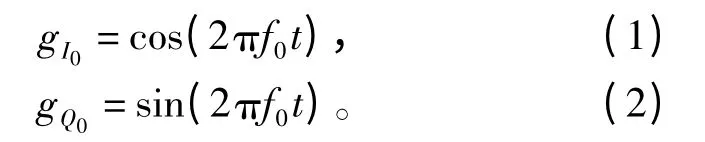
式中，t 为时间，f0为频率值，g 为正余弦双原子。

在匹配运算的过程中，每次在选择最优原子时，按照式(3)进行分解:

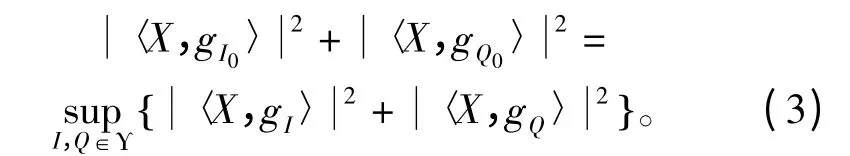
在求得一对最佳的原子后，按照式(4)重新组建新的合成原子:

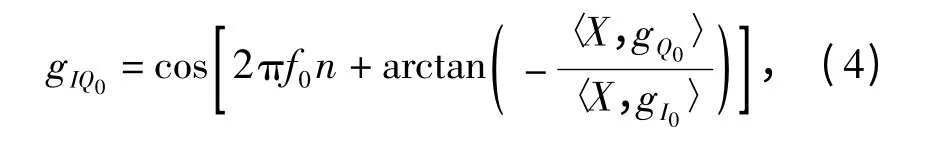
合成原子的频率取最佳原子的频率，而合成原子相位的正切值是正余弦原子相干运算的比值。将最佳匹配后的残余分量继续进行匹配搜索次优原子。根据式(5)的信号由原子重新组合而成:

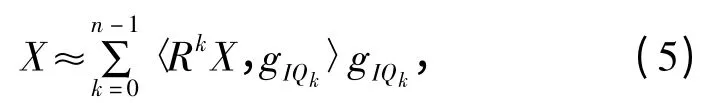
最终将信号分解为n 次最佳原子的分量之和的形式。数字锁定放大器处理信号的过程如图2 所示，将稀疏分解算法运用到锁定放大器，参考输入信号使用稀疏分解算法中原子库的原子，运用匹配追踪算法检测出有用信号。

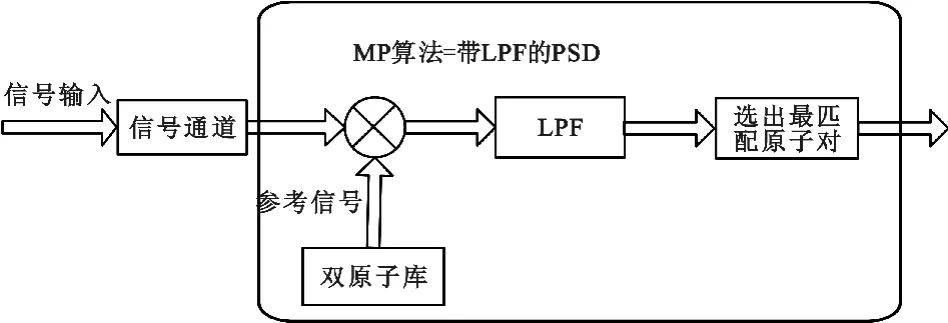
图2 锁定放大器处理信号流程图Fig.2 Lock－in amplifier signal processing flow

采用稀疏分解算法实现的数字锁定放大器可以实现信号的自动捕获跟踪，但是稀疏分解算法的计算复杂度随着原子库的规模增加而增加［11－12］。对信号的搜索精度要求提高时，计算复杂度将成倍增加。针对以上特点，我们提出运用非线性方法对锁定放大器的搜索过程进行改进，在不增加计算复杂度的情况下增加锁定放大器的搜索精度。

3 基于混沌振子微弱信号检测算法

针对Duffing 振子对微弱信号具有敏感性的特点，采用非线性系统进行信号检测时，Duffing 振子的一般形式为［8］

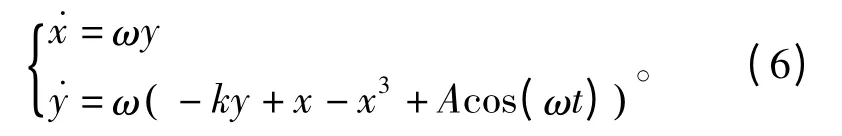
式中，k 为阻尼比，－ x+x3为非线性恢复力，Acos (ωt)为周期策动力，ω 为周期策动力的频率。

将阻尼比k 设为固定值，周期策动力的幅值能够控制Duffing 振子系统的状态:调节A 的取值使系统处于混沌状态;增加A 的数值，当超过阈值Ad时，系统以周期策动力的频率包围所有鞍点和焦点进行大尺度的周期振荡［9］。调节周期策动力幅值A，使A=Ad，此时系统处于混沌临界状态，将同频率的待测微弱正弦信号Accos(ωt+φ)加入系统式(7)中的总周期策动力变为

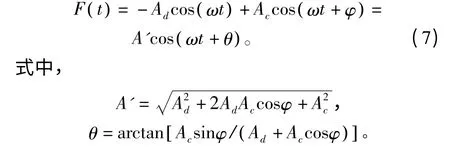
系统对周期策动力幅度敏感，总周期策动力是内置策动力和输入信号的矢量和。图3 表示周期策动力的矢量叠加过程，图中向量AB表示内置周期策动力，向量BC表示输入信号，AC是它们的矢量和，代表总的周期策动力。令lAB=lAD，那么长度d 为总的周期策动力幅值增加量，由于γ 远远大于α，∠1趋近于零，∠2 趋近于直角，∠θ 等于∠θ'，幅值增加量d=α·cosθ'≈α·cosθ。

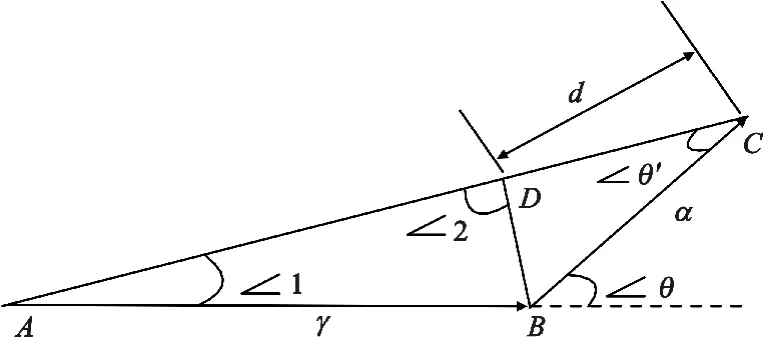
图3 周期策动力矢量图Fig.3 Cycle power vector diagram

Duffing 振子系统的状态受周期策动力的控制，当策动力增大到相态变化的阈值时，周期策动力的微小变化都可以使混沌振子系统发生相变。利用这一特性，可以在强噪声背景下检测微弱信号的存在。

4 基于联合方法的信号检测算法

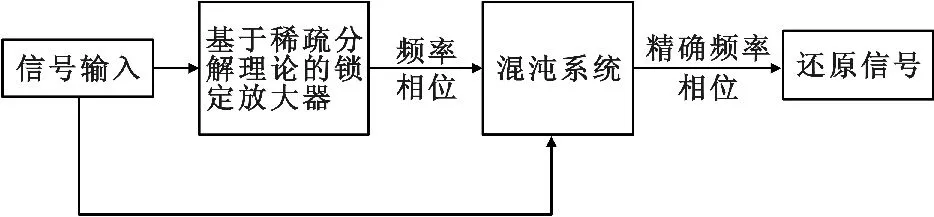
图4 联合检测系统Fig.4 Joint detection system

检测方法描述如下:将微弱信号输入基于稀疏分解理论改进的数字锁定放大器，此时的数字锁定放大器检测信号的精确度不高，只能检测出精度较低的频率参数ω，产生频率偏差Δω，频率偏差达到1 Hz，不能够满足微弱信号的检测精度要求，因此提出将混沌系统应用至锁定放大器中的办法，以提高检测精度。

设计适合微弱信号的混沌系统:检测出的频率ω 作为混沌系统的内置周期策动力频率，此时系统的内置策动力为Acosωt。

检测信号作为外部对系统叠加的驱动力输入到混沌检测系统，表示为Bcos [(ω+Δω)t+φ ]。

总周期策动力表示为

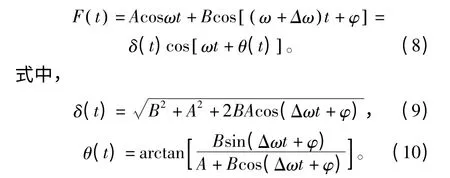
对外加的周期策动力按式(11)进行变换:

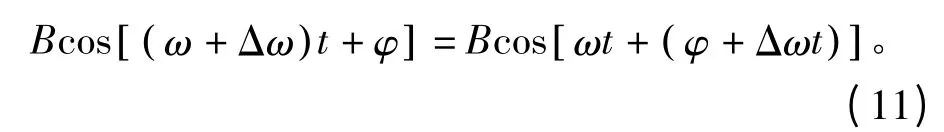
式中，频偏分量转移到相位部分，即θ'=θ+Δωt。

当A ＞＞B 时:

除了改善生态环境、塑造绿带景观外,环城绿带植物群落的功能也需随着城市更新而不断丰富和完善。上海市绿化局牵头研究编辑的《上海市绿道专项规划》[4]中提到计划在2020年于环城绿带百米林带内建设绿道,供市民进行日常活动。近年来,人们休闲娱乐需求日益增长,环城绿带百米林带因其区位条件好、消费成本低、交通便捷,将成为居民日常休闲活动的最佳去处[5]。然而目前针对上海环城绿带植物群落的研究中,尚缺乏对于植物群落与游憩的相关研究。

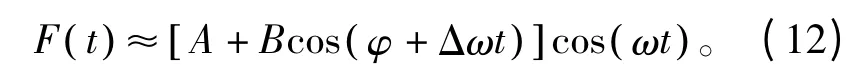
式中，策动力的幅度值受时间t 影响，随着时间的推移出现周期性变化:

(1)(2πK－π/2)＜ (θ+Δωt)≤ (2πK+π/2)时，微弱信号使混沌系统的周期策动力变大;

(2)(2πK+π/2)＜ (θ+Δωt)≤(2πK+3π/2)时，微弱信号使混沌系统的周期策动力变小。

混沌系统的策动力随着时间变化，当策动力没有达到系统变化的阈值Ad时，系统处于混沌态，而当策动力超过了阈值Ad时，系统进入周期态，由此产生间歇性混沌运动。间歇性混沌运动的变化周期是ΔT=2π/Δω。采用混沌系统检测信号的频率差也是在于提高频率的精度值，频率差值越小，间歇性混沌运动越容易测量。改进后的锁定放大器通过测量间歇性混沌现象的周期，最终检测出信号的精确频率值。

5 实验验证

为了验证基于稀疏分解算法的锁定放大器，对比不同频率精度的信号在锁定放大器中的检测性能。设定待检测的微弱信号为

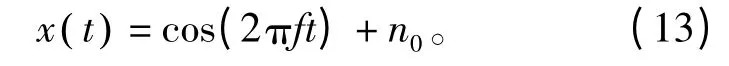
式中，n0表示噪声，t 表示时间，f 表示信号频率。

f 分别设定为49.9 Hz、49.95 Hz、50 Hz 3 组值，代表a、b、c 3 种信号。信噪比为－20 dB，锁定放大器中稀疏分解原子库的频率范围设定为1 Hz～1 MHz，步长为1 Hz。

采样点为5000 点时，输入3 种信号至锁定放大器，锁定放大器输出稀疏分解系数。图5(a)的首轮分解系数为30.9，次轮分解系数为4.8，首轮稀疏分解系数远高于次轮稀疏分解系数，首次稀疏分解检测到频率为50 Hz。

图5(a)、(b)、(c)的首轮稀疏分解系数分别为30.9、79.6、89.4，对检测3 种信号的分解系数陡降程度排序为c、b、a。可以看出，若是锁定放大器检测到的信号频率存在差值，稀疏分解系数会随频率差值的增大而降低。

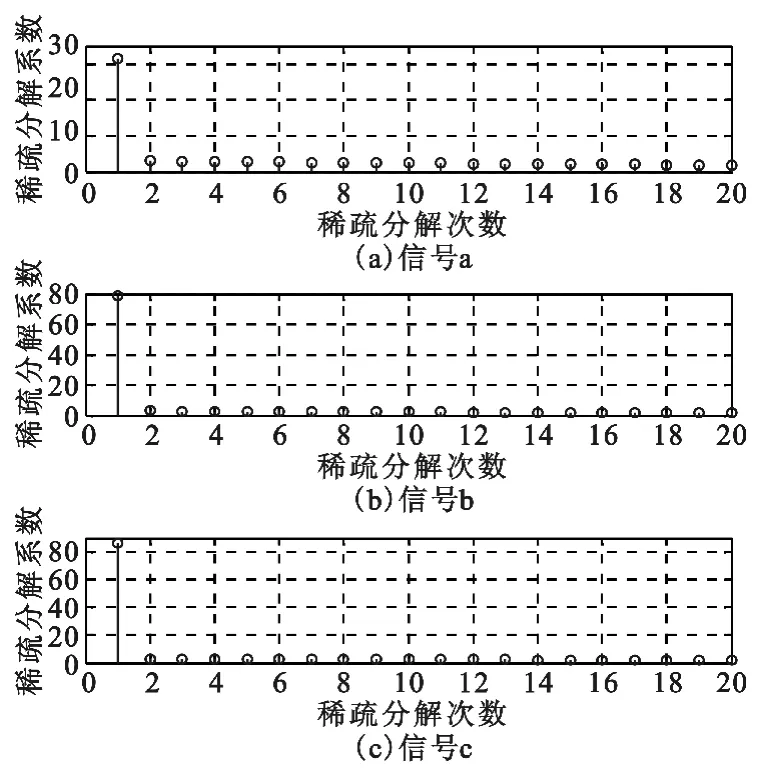
图5 锁定放大器的分解系数Fig.5 The decomposition coefficient of lock－in amplifier

为了验证改进后的锁定放大器的性能，将信号信号a、b、c 输入混沌系统进行精确检测，混沌系统内置驱动力为50 Hz。由图6(c)可知，c 信号的混沌系统一直处于大尺度周期状态，证明没有产生频偏。由图7(a)、(b)可知，a、b 信号的混沌系统处于间歇性混沌状态。对输出信号进行功率谱熵值计算，由图8(a)可知，a 信号的间歇性混沌状态周期是10 s，得出a 信号频率偏差为0.1 Hz，待测信号a 的频率是50 ±0.1 Hz。由图8(b)可知，b 信号的间歇性混沌状态出现周期是20 s，b 信号频率偏差为0.05 Hz，待测信号b 的频率是50 ±0.05 Hz。再将这两种频率的正弦波与待测信号做相干计算进行比较，得出a 信号的频率是49.9 Hz，b 信号的频率是49.95 Hz。

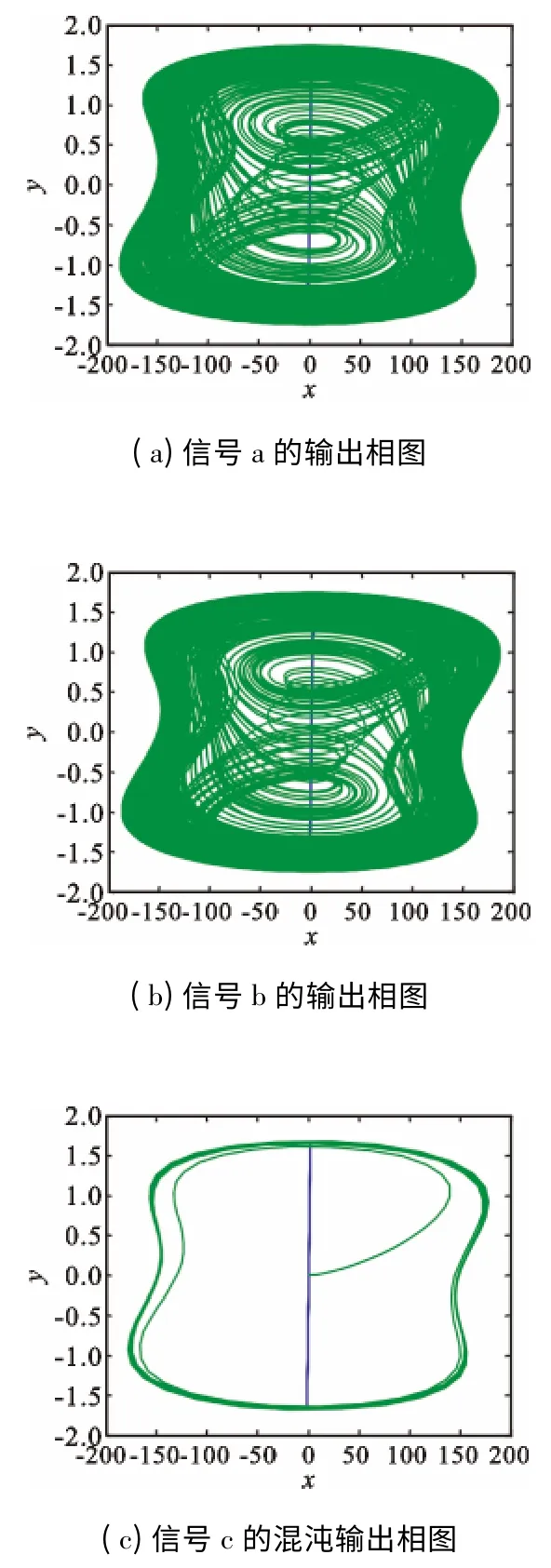
图6 混沌系统输出相图Fig.6 Chaotic system output phase diagram

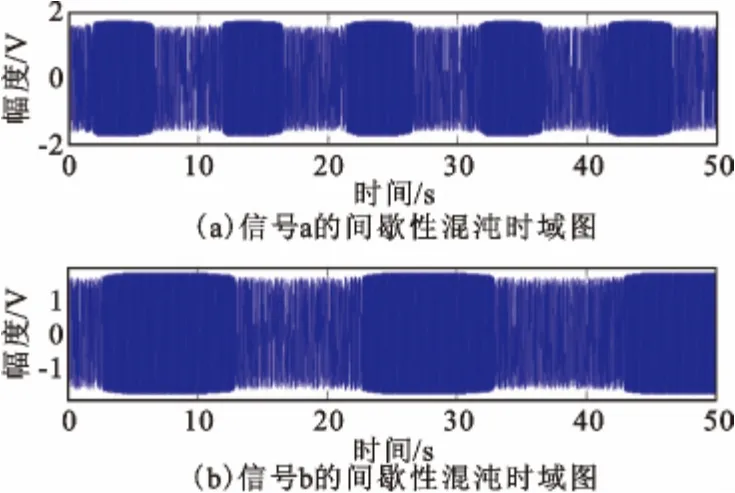
图7 混沌系统输出时域图Fig.7 The time domain output diagram of chaotic system

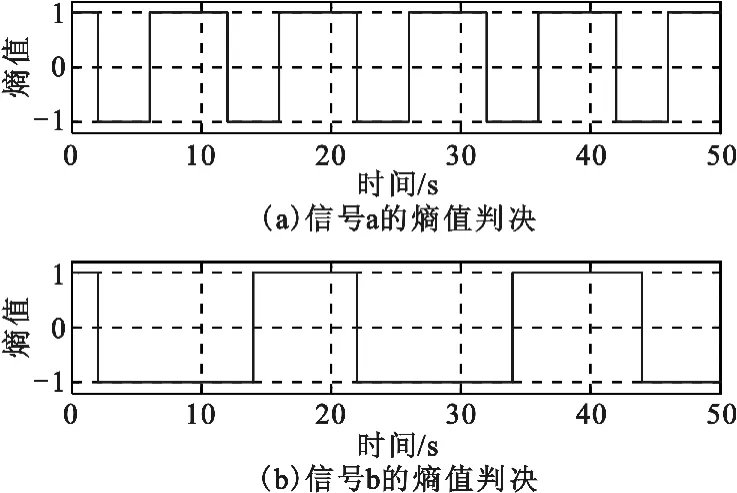
图8 混沌系统的熵值判决Fig.8 The entropy value judgement of the chaotic system

针对目前的研究，文献［2－5］分析了锁定放大器中频率跟踪的精度，其中文献［2］最具代表性。文献［2］设计了一种基于LabVIEW 开发平台的虚拟数字锁定放大器，引入自动频率跟踪模块大大降低了待测信号与参考信号频率的失配程度。在不计算法复杂度的情况下以及信号的信噪比为－20 dB的相同条件下，在1 kHz时的频率跟踪的最大跟踪误差达到0.02%，基于混沌阵子和稀疏分解联合算法的微弱信号检测算法的频率跟踪精度为0.05 Hz，经过换算跟踪精度在一个数量级上，相比文献［2］性能相当。但是，文献［2］的采样点数设置20 000，相比本文的5000 采样点数，其检测精度会有所下降，因此在跟踪精度上本文算法具有一定的优势;并且在信噪比更低的情况下，本文算法仍具有较高的跟踪精度，如表1 所示，而文献［2］中并没有进一步论述。

为了验证改进后锁定放大器的可靠性，将信号a 的信噪比从－20 dB降到－35 dB，进行蒙特卡洛仿真实验。经过8000 次蒙特卡洛实验，具体仿真性能如表1 所示，当信道条件在－20 dB的情况下，锁定放大器检测信号成功率达到100%，能够较优地满足微弱信号的检测要求。

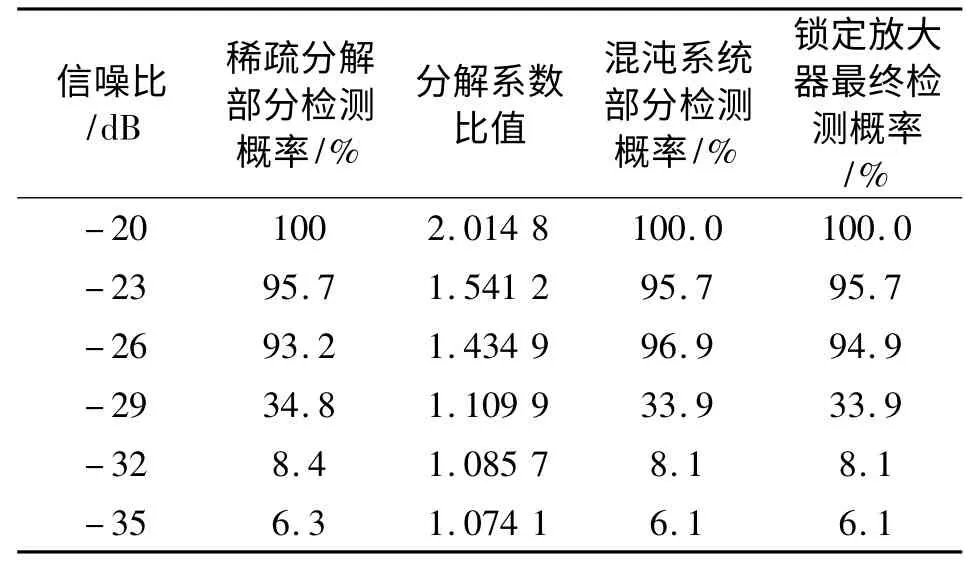
表1 采样点为5000 点时的蒙特卡洛检测结果Table 1 The Monte Carlo test results when the time sampling points are 5000

6 结束语

在数字锁定放大器中引入Duffing 振子联合稀疏分解理论的微弱信号检测方法，实现了对微弱信号的精确检测，在信噪比为－20 dB 的情况下，检测信号的频率精度为0.05 Hz，尤其在更低信噪比的情况下，相比已有的信号检测方法性能得到了大幅提高，为微弱信号检测提供了一种有效的非线性方法。本文是针对信号的频率进行锁定，在以后的研究中可以针对信号的其他参数进行非线性检测。

［1］高晋占.微弱信号检测［M］.北京:清华大学出版社，2004:154－176.GAO Jinzhan.Weak signal detection［M］.Beijing:Tsinghua university Press，2004:154－176.(in Chinese)

［2］赵玲，田小建，梁磊，等.基于自动频率跟踪的虚拟数字锁相放大器［J］.吉林大学学报，2012，30(1):5－11.ZHAO Ling，TIAN Xiaojian，LIANG Lei，et al.Virtual digital lock－ in amplifier based on automatic frequency tracking［J］.Journal of Jilin University，2012，30(1):5－11.(in Chinese)

［3］王坤朋.微弱信号检测的盲源分离方法及应用研究［D］.重庆:重庆大学，2014.WANG Kunpeng.Methodologies and Applications of Weak Signal Detection Based on Blind Source Separation［D］.Chongqing:Chongqing University，2014.(in Chinese)

［4］蒋世文，张天骐，代少升，等.基于稀疏分解的自适应数字锁定放大器微弱信号检测方法［J］.西南大学学报，2010，32(1):160－167.JIANG Shiwen，ZHANG Tianqi，DAI Shaosheng，et al.A Weak Signal Detection Method of Adaptive DigitalLock－in Amplifier Based on Sparse Decomposition［J］.Journal of Southwest University，2010，32(1):160－167.(in Chinese)

［5］刘寅.基于稀疏信号重构的空间谱估计算法研究［D］.西安:西安电子科技大学，2012.LIU Yan.Research on algorithms of spatial spectrum estimation based on sparse signal reconstruction［D］.Xi'an:Xidian University，2012.(in Chinese)

［6］MALLAT S G，ZHANG Z.Matching pursuit with time－frequency dictionaries［J］.IEEE Transactions on Signal Processing，1993，41(12):3397－3415.

［7］CHEN S，DONOHO D，SAUNDERS M.Atomic Decomposition by Basis Pursuit［J］.SIAM Journal on Scientific Computing，1999，20(1):33－61.

［8］李月，徐凯，杨宝俊.混沌振子系统(L－ Y)与检测［M］.北京:科学出版社，2007.LI Yue，XU Kai，YANG Baojun.Chaotic vibration subsystem(L－ Y)and testing［M］.Beijing:Science Press，2007.(in Chinese)

［9］李月，徐凯，杨宝俊，等.混沌振子系统周期解几何特征分析与微弱周期信号的定量检测［J］.物理学报，2008，57(6):3353－3358.LI Yue，XU Kai，YANG Baojun，et al.Analysis of the geometric characteristic quantity of the periodic solutions of the chaotic oscillator system and the quantitative detection of weak periodic signal［J］.Acta Physica Sinica，2008，57(6):3353－3358.(in Chinese)

［10］胥小波，郑康锋，李丹，等.新的混沌粒子群优化算法［J］.通信学报，2012，31(1):24－31.XU Xiaobo，ZHENG Kangfeng，LI Dan，et al.New chaos－particle swarm optimization algorithm［J］.Journal on Communications，2012，31(1):24－31.(in Chinese)

［11］尹明，尹忠科，王建英.利用蚁群算法实现基于MP 的信号稀疏分解［J］.计算机工程与应用，2006，42(36):47－48.YIN Ming，YIN Zhongke，WANG Jianying.Signal Spar se Decomposition Based on MP［J］.Computer Engineering and Applications，2006，42(36):47－48.(in Chinese)

［12］LIU T.Study on casting ultrasonic signal extraction algorithm based on improved MP［C］// Proceedings of Future Computer and Communication(ICFCC－2010).Wuhan:IEEE，2010:115－118.