弹簧质量对弹簧振子周期的影响研究
2013-01-12 05:21:32王文涛
物理通报 2013年11期
王文涛
(江苏省镇江市第一中学 江苏 镇江 212000)
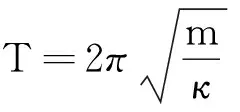
1 理想弹簧振子的周期

图1
如图1所示的弹簧振子,除振子外不计其他质
量,不计一切摩擦,根据牛顿第二定律可得
ma=-κx
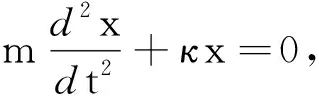
x=Acos(ωt+φ)
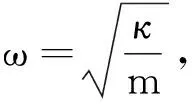
2 考虑弹簧振子质量的振子周期
若考虑弹簧振子的质量,可以通过振动过程中的能量求解其周期.如图2所示,设弹簧质量为m0,在距离固定点O距离为x处取一小段微元dx,设弹簧长度为L,那么这段微元的质量为dm,那么

图2
所以弹簧的总动能为
此时振子的动能为
系统的总动能为
若将其等效为一个理想的弹簧振子,其等效振子质量为M,则应该满足
所以可得
因此可得考虑弹簧质量的振子周期为
其周期大于理想弹簧振子的周期.
以上结论可以通过实验验证,取弹簧质量小于振子质量,通过多次周期的测定可以计算出m0前的系数,约为0.3~0.35,与理论结果基本相符.
3 实际弹簧振子的周期
在上述研究中,认为弹簧质量较小,并且弹簧的伸长是均匀的.但是,如果弹簧的质量同振子的质量类似,或者弹簧的长度较长,弹簧的变化实际并非呈线性变化.此时由于振子的运动在弹簧中实际上形成了纵波.所以要解决实际弹簧振子的周期可以利用弹簧的纵波解来辅助研究.
由纵波传播方程可以得到,考虑弹簧质量振子的运动方程实际上是无穷多个简谐运动的合成,其运动方程如下


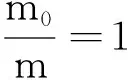
弹簧的等效质量为0.35m0.
4 结论
如果弹簧振子的质量远小于振子的质量,那么可以当作理想的弹簧振子,其周期公式满足T=

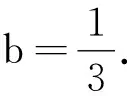
参考文献
1 吴百诗.大学物理.西安:西安交通大学出版社,1994.244~245
2 徐延燕.弹簧振子近似作简谐运动的条件.河北师范大学学报,1997,21(1)
猜你喜欢
金桥(2022年4期)2022-05-05 06:09:50
中学生数理化·自主招生(2021年8期)2021-05-30 10:48:04
人大建设(2018年7期)2018-09-19 06:18:58
商周刊(2018年15期)2018-07-27 01:41:16
商周刊(2018年11期)2018-06-13 03:41:52
数学物理学报(2018年1期)2018-03-26 08:16:58
石油地球物理勘探(2017年2期)2017-11-23 06:01:47
电测与仪表(2016年18期)2016-04-11 11:30:30
浙江大学学报(工学版)(2015年6期)2015-03-01 01:18:34
物理实验(2015年10期)2015-02-28 17:36:55

