简约不简单

（浙江省宁波市第二中学315010）

简约不简单

李建明（浙江省宁波市第二中学315010）

在高三复习中，高考真题有着不可取代的作用，但是，如何用好高考真题，发挥真题的作用，让真题的潜能被完全激发，一些教师采用一题多解，一些教师采用一题多变，可谓是“八仙过海，各显神通”。但是，无论采用什么方法，找到题目背后的本源和知识生长点，才是利用高考真题的关键，“知一题而通一类”，特别是在高三复习阶段，构建理性思维、形成清晰的知识网络，才能事半功倍。本文试以一道高考真题为例进行剖析。

考题展示

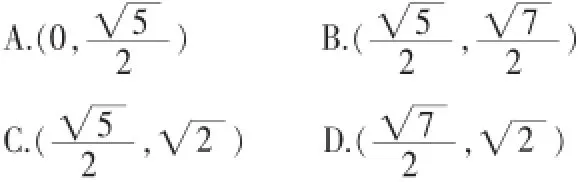
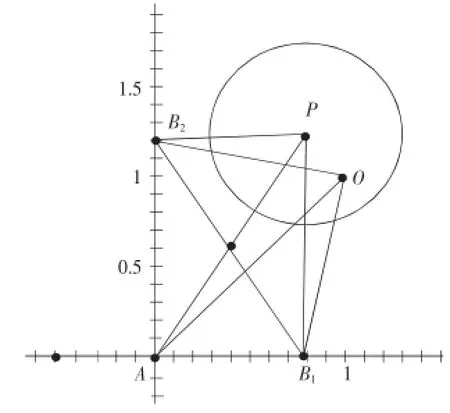
解法一（解析法）

解：设B1（a，0），B2（0，b），P（a，b），O（x，y）

学生在尝试解此题的时候，绝大多数能想到应用该方法，但是真的能理清几个模长之间关系的学生少之又少。已知三个模的坐标形式和要求的模的坐标形式，其实是四元关系，那么要求的模能不能用已知的模来表示呢？我们可以发现：这样的关系就能得到

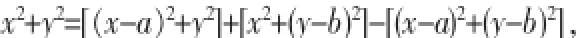
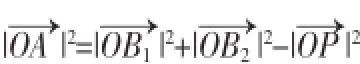
实践中，也有向量功底深厚的学生给出了如下解法：

解法二（基向量法）

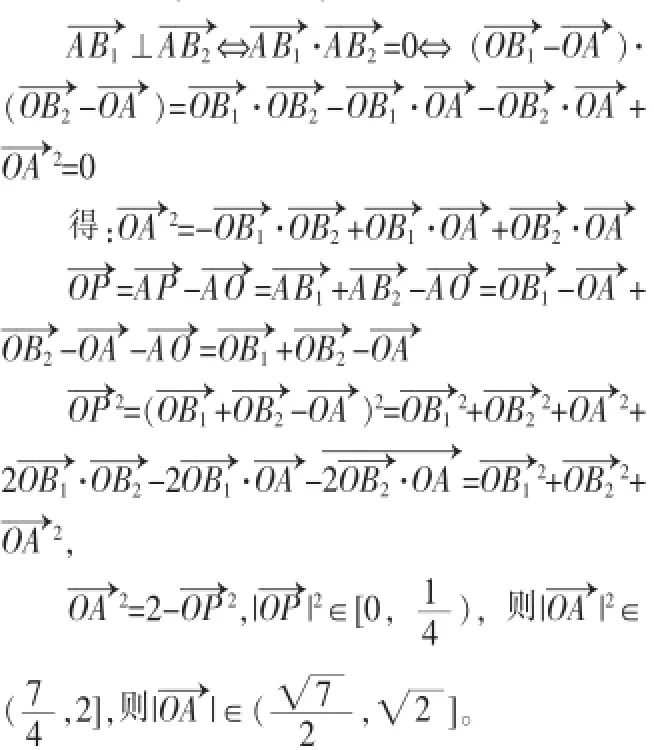
这两种解法对于学生来说都可以接受，平常的教学也是根据向量垂直用坐标系或者选择适当的基底。如果此题的剖析到此为止，那就只完成了一题多解，但是，我们真的找到了此题的本源吗？我们真的找到了让学生的知识和能力增长的生长点吗？

对比两种解法我们会发现其实解法一和解法二都出现了一个式子，分析解法，发现此等式是解决本题的一个关键，也是本题的一个大背景所在，那么，这是一个必然还是一种巧合，此结论是否具有普遍性？

定理：平面内任意一点到矩形两组相对顶点距离的平方和相等。

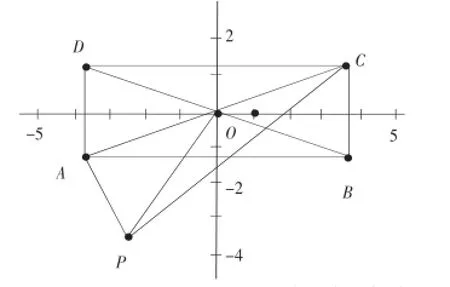
证明：设矩形ABCD的四个顶点坐标分别为（a，b），（a，-b），（-a，-b），（-a，b）

平面上任意点P（x，y），则

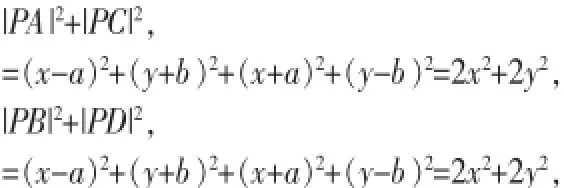
即|PA|2+|PC|2=|PB|2+|PD|2，得证。

通过发掘，我们找到了此题的一个本源，也是此题的一个生长点，学生通过探究此题，思维上得到了发展，继续引导，由于本题的本源是上述定理。让知识继续生长，在这个定理的背景下，能否将条件一般化呢？

推广一：

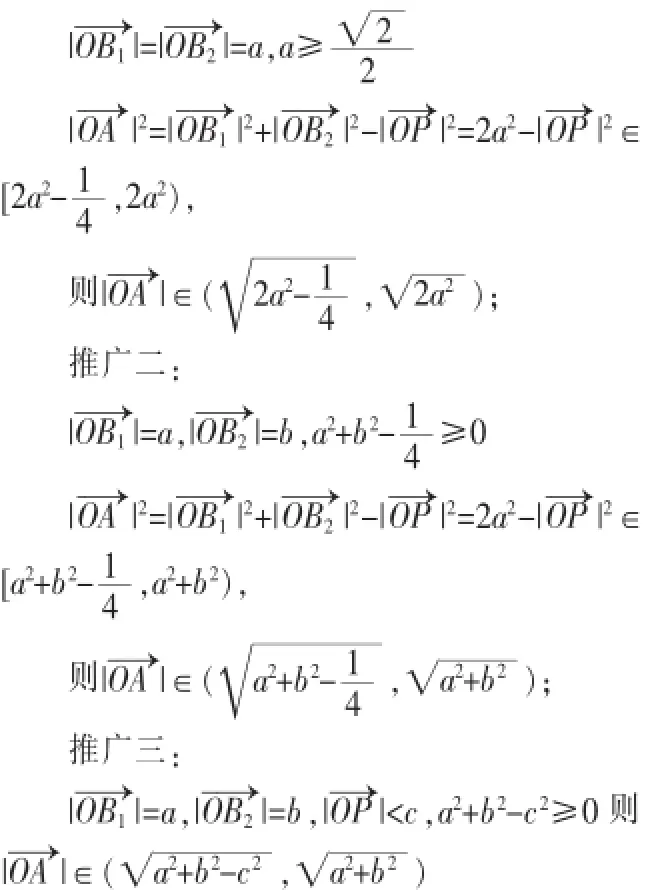
至此，学生的思维活动也进入了一个高潮，思维的活跃性被高度激发，而真题的价值也被充分地挖掘。用真题，不是为了解题，其最大的价值在于提升思维，用真题，不仅要知道真题的去脉，更要弄清来源。会一题而知一类，是解题教学中应当追求的一种境界。

（责编 赵建荣）