高中数列教学的数学思想

（江苏省仪征市第二中学211400）

高中数列教学的数学思想

曹国弘（江苏省仪征市第二中学211400）

当前高中学生对数学学习敬而远之，教师仍旧采用传统教学方法，在教学过程中未从学生角度考虑，时常一意孤行，按照自己的方式展开教学。数列是高中数学的重要内容，也是重难点之一，学生在数列的学习中往往难以跟上教师的进度，对一些数列问题理解不够，久而久之便失去学习信心。教师在教学中应该从数学思想的高度教导学生，让学生掌握正确的数学思想方法。

一、数列中的函数思想及其应用

从函数定义来看，数列本身就是一种特殊的函数，因此解决数列问题其本质就是利用相关的函数思想探究问题。函数讲究的是整体思想，即从整体的角度看待问题，放开眼光，尤其是一些题意不明、难以直观找到解题方法的难题，很多学生在解题中常常摸不着头脑，不知从何下手。多数原因是学生过于注重某个细节，未从整体上看待问题，对很多公式的运用缺乏灵活性。为了提高学生对数列知识的认识，掌握整体看待问题的能力，我在此，利用相关数学函数思想进行问题的解答。对于等差数列的求和公式Sn=na1+n（n-1）d／2=An2+ Bn，观察该公式发现，其符合二次函数形式，因此，对等差数列的求和公式可利用二次函数思想进行探究。例如，在某个等差数列数列中，其前n项之和为Sn=m，前m项之和为Sm=n（其中m和n不相等），在此条件上求前Sm＋n。该题中，根据求和公式可知Sm＋n=a1（m＋n）+（m＋n-1）（m＋n）d／2=（m＋n）（a1+（m＋n-1）d／2），从该公式中可以看出，欲知Sm＋n只需要求解a1+（m+n-1）d／2，根据题意通过Sn及Sm构造出a1+（m＋n-1）d／2，并进行计算。在此基础上利用整体思想及函数思想，结合等差数列中前n项之和的函数关系，根据公式可知其在图像中必经过（0,0）点，并以此为突破点可以找到几种解题方法，如假设该数列的公差为d，由题意可列出

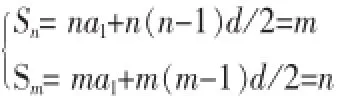
两式相减可得出Sm-Sn=ma1+m（m-1）d／2-na1+n（n-1）d／2=（m－n）a1+（m＋n-1）（m＋n）d／2，由于m与n不等，因此（m－n）a1+（m＋n-1）（m＋n）d／2=-1，所以Sm＋n=a1（m＋n）+（m＋n-1）（m＋n）d／2=（m＋n）（a1+（m＋n-1）d／2）=-（m＋n）

二、递推思想在高中数列中的应用

递推思想是数学中常用的思想方法之一，用于解答一些较为复杂的通项问题，递推中包含两种常用的数学方法，一种是累加法，另一种是累积法。

累加法，顾名思义，就是将是数列中的各项累计求和，并从中找到一些解决问题的突破口，简化解题步骤。在数列中，如果该通项满足an-an-1=f（n）（其中f（n）可以进行裂项）时就能够采用累加的方式进行求解。例如，在一数列｛an｝中，首项a1=1，当n大于等于2时，an=an-1+ 1／n（n+1），求该数列的通项公式。

该题中，当n大于等于2时，an=an-1+1／n（n+ 1），由此可知an－an-1=1／n（n+1）=1／n-1／（n+1），利用累加思想求解可得出an=（an－an-1）+（an-1-an-2）+…+（a3-a2）+（a2-a1）=（1／n-1／（n+1））+（1／（n-1）-1／n）+…+（1／3-1／4）+（1／2-1／3）+1=1／（n+1）+1／2=3／2-1／（n+1）

累积法与累加法思想类似，即当an／an-1=g（n）具有某种关系时就能利用an=an／an-1＊an-1／an-2＊…a3／a2＊a2／a1＊a1来求出an。

三、方程思想在数列中的应用

方程思想是数学中常用的解题思想，即利用方程组的形式求解未知量，数列中的几个常用量为a1，n，d（q），an，Sn，在实际求解过程中可利用其中已知的三个量结合方程求解另外几个未知量，在这里就可以利用方程思想进行数列知识的求解。例如，在一等差数列｛an｝中，其公差为一正数，且a3＊a7=-12,a3+a7=a4+a6=-4,根据此条件求解该数列的前n项和。

在该题中由于存在如下关系：a3＊a7=-12, a3+a7=a4+a6=-4，因此可判断出a3和a7是x2+4x-12=0的两个解，由题意知公差d＞0，解此方程可得a3=-6，a7=2，将结果带入题意中的两个关系式

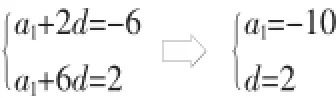
将得到的结果带入等差数列前n项和公式可得Sn=-10n+n（n-1）。

四、归纳法在数列中的应用

数学归纳法主要指通过个别数学案例归纳出通用性的结论，并通过相关数学方法进行证明。数学归纳法的应用一般步骤为观察分析、归纳总结、假设猜想、证明结论。例如，在一数列｛an｝中，an＞0（n＞1），a0=1，an-1=an（4-an）／2，求证an＜an+1＜2。

在该题中，当n=1时，a0=1，a1=a0（4-a0）=3／2，a0＜a1＜2，此时正确。

假设当n=k时，ak-1＜ak＜2，当n=k+1时，akak+1=ak-1（4-ak-1）／2-ak（4-ak）／2=2（ak-1-ak）-（ak-1-ak）（ak-1+ak）／2=（ak-1-ak）（4-ak-1-ak）／2

又有ak-1-ak＜0,4-ak-1＞0,所以ak－ak-1＜0,

又ak+1=ak（4-ak）／2=［4-（ak-2）2］＜2

即n=k+1时命题正确，所以对一切n满足题意条件是均存在an＜an+1＜2。

五、转化思想在数列中的应用

高中生在日常学习中遇到的数列问题比较抽象，在解决一些应用题时中常会遇到瓶颈，难以找到突破口，此时可以尝试采用转化思想，将抽象的实际问题转化为数列问题，成为高中生容易理解的形式。然后再使用数列相关函数关系进行求解。例如，某地区本月突发流感，本月1号感染人数为20人，在此基础上以后每天的感染人数均增加50人，医疗机构为控制感染人数，采取某项有效预防措施，从本月某天起日感染人数平均相比前一天下降了30人，截至本月30号（按30天计算），该地区总计感染人数为8670例，求该月份哪天感染流感人数最多，并求出该天具体感染人数。

通过分析题意可以看出，该题是等差数列相关知识的应用，从题意中可以看出，本月1号到n号，每日流感感染人数可以构成一项等差数列，从n+1天开始到该月最后一天，又可构成公差不同的等差数列，假设第一个数列为｛an｝,第二个数列为｛bn｝，通过题意可知，a1=20，d1=50，b1=50n-60，d2=-30。bn=（50n-60）+（n-1）（-30）=20（30-n）-30=570-20n。所根据总感染人数可列出：（20+50n-30）n／2+［（50n-60）+（570-20n）］（30-n）／2=8670，通过计算可以得出一个二次函数n2-61n+588=0，求解该而从方程可以得出n1=12，n2=49，结合实际，该月只有30天，因此可解的该月12日感染者数量最多，人数为570人。在该题中可以看出，一些实际中比较复杂的问题可以转化为数列知识进行解答，这不仅是数学中转化思想的应用，还是数列知识的实际应用，在解决问题的过程中，可以利用适当的方法以及科学的思想将其转化为数列来解决。

数列是高中数学的难点知识之一，很多数列题型比较抽象，学生理解起来具有一定难度，因此在教学过程中教师应该让学生掌握必要的数学思想，利用通用的数学思想解决常见的问题，培养学生的开放性思维，为学生后续学习奠定坚实的基础。

（责编 赵建荣）