例说多元初等函数结构的化解策略

●江志杰(惠安县第三中学福建惠安362100)

例说多元初等函数结构的化解策略

●江志杰(惠安县第三中学福建惠安362100)

以xi(其中i=1，2，…，n)为变量的基本初等函数，经过有限次的四则运算或复合运算，且可用一个式子表示的函数y=f(x1，x2，…，xn)，称为多元初等函数.近年来各地高考屡屡以多元函数模型为载体，综合考查函数的单调性、最值、导数及其应用等基础知识，着力考查推理论证能力、运算求解能力、知识交汇迁移能力和创新意识等，有效考查函数与方程、化归与转化、分类与整合、数形结合等数学思想.这对以一元函数为主体的传统函数教学有着极大的挑战和跨越，为此笔者着重从多元初等函数结构入手，谈谈其化解策略.

1 配凑换元转化为一元函数

有些二元函数y=f(x1，x2)经过适当的整理变形后，可令其中或t=x1x2或t=x1±x2等，转换为关于t的一元函数y=φ(t)来解决，这是一种最常规的化归策略.

例1设A(x1，y1)，B(x2，y2)(其中x1＜x2)是函数f(x)=xlnx－x+1图像上的2个点，且曲线f(x)在点T(t，f(t))处的切线与直线AB平行，求证:x1＜t＜x2.

解由kAB=f'(t)得

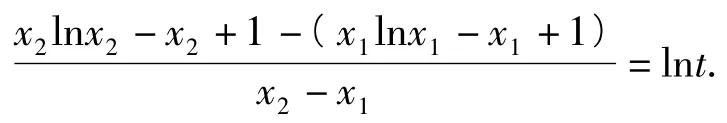
本题关键是证明关于t的函数

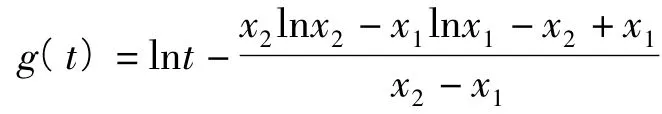
在(x1，x2)上有零点.注意到g(t)在(x1，x2)上单调递增，于是问题转化为判断端点值g(x1)，g(x2)的符号.而

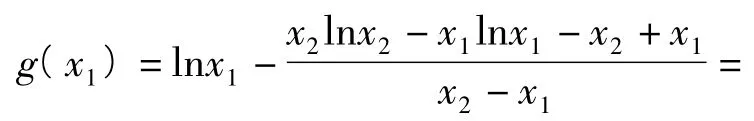
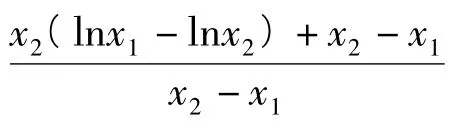
的右端是二元“准齐次”的分式结构，分式上下同除以x2得

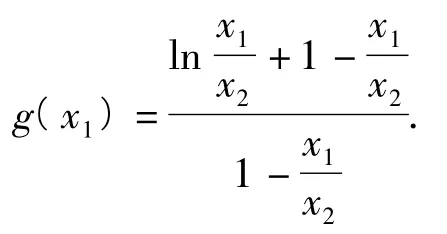
点评解决本题的另一关键就是要明确字符t，x1，x2，λ的“身份特征”，如在初始函数

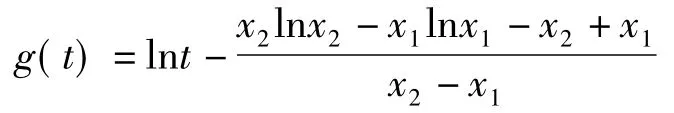
中t是自变量、未知量，x1，x2是常量;然而在二元函数

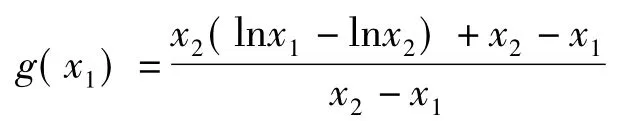
中，x1，x2是自变量的“身份”;λ是换元简化后一元函数的自变量.因此，只有把握前后函数的“主元”，方能抓住解决问题的核心和本质.

变式设A(x1，y1)，B(x2，y2)(其中x1＜x2)是函数f(x)=eax－x(其中a≠0)图像上的2个点，记直线AB的斜率为k，问:是否存在x0∈(x1，x2)，使得f'(x0)＞k成立?若存在，求x0的取值范围;若不存在，请说明理由.

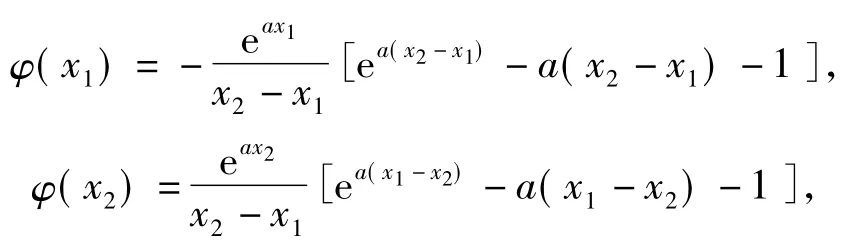
点评本题解析中φ(x1)，φ(x2)的配凑整理和分离一元函数F(t)=et－t－1的模型是问题解决的最大“亮点”.

2 更换主元演变为一元函数

多元初等函数y=f(x1，x2，…，xn)经常根据实际需要，比如将x1视作变量，其余x2，…，xn视作常量，即可实现转化为一元函数y=φ(x1)的形式.

如例1中:

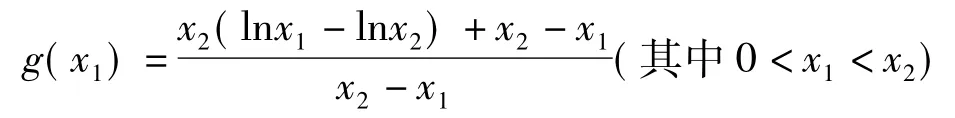
的符号由分子x2(lnx1－lnx2)+x2－x1的符号所确定.若将x1视作自变量、将x2视作常量，则可得一元函数

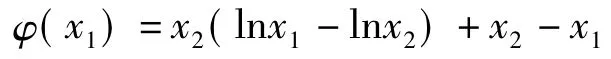
(其中x1∈(0，x2)，x2为常量)，对x1求导得

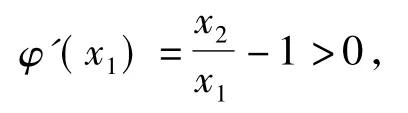
故函数φ(x1)=x2(lnx1－lnx2)+x2－x1在(0，x2)上单调递增，且用x2替代x1得端点值φ(x2)=0，于是φ(x1)＜0，g(x1)＜0.同理可得g(x2)＞0.

3 利用单调性定义建构函数

某些二元不等式左、右2边具备鲜明的同构性，比如f(x1)＞f(x2)或等结构的不等式经常可建构函数模型，转化为函数的单调性问题加以解决.

例2设f(x)=ex－a(x+1)(e是自然对数的底数，e=2.718 28…)，且f'(0)=0.

1)求实数a的值，并求函数f(x)的单调区间;

2)设g(x)=f(x)－f(－x)，若曲线y=g(x)上任意不同的2个点连线的斜率恒大于实数m，试求实数m的取值范围.

分析1)a=1，f(x)的单调递增区间为(0，+∞);单调递减区间为(－∞，0).

2)依题意得，对任意x1，x2∈R(其中x1＜x2)，恒有成立，即

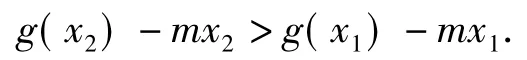
构造函数F(x)=g(x)－mx，则F(x)在R上单调递增.因此

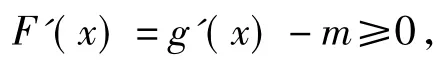
即m≤g'(x)在R上恒成立.而

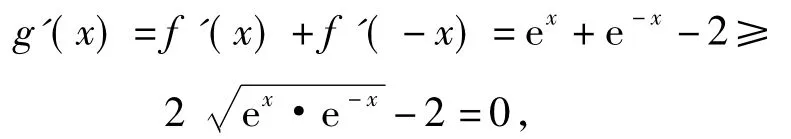
当且仅当x=0时，取到等号，故m≤0.

4 挖掘目标函数式几何意义

有些多元函数y=f(x1，x2，…，xn)本身蕴含着某种特殊结构(如2个点间的距离或距离平方或2个点的斜率等形式)，具有丰富的几何意义.倘若我们能充分发挥数形结合思想，必将巧妙有效地开辟新的解法空间.

例3若实数a，b，c，d满足(b+a2－3lna)2+(c－d+2)2=0，则(a－c)2+(b－d)2的最小值为______.

解目标多元函数(a－c)2+(b－d)2表示点(a，b)与点(c，d)之间距离的平方，由已知条件得

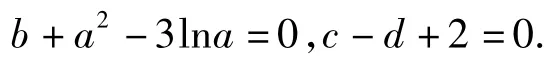
即点(a，b)，(c，d)分别是曲线y=－x2+3lnx与直线x－y+2=0上的动点，因此本题的关键是求曲线y=－x2+3lnx上的点与直线x－y+2=0上点的距离的最小值.设曲线y=－x2+3lnx在点P(m，n)处的切线与直线x－y+2=0平行，则

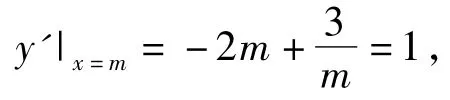
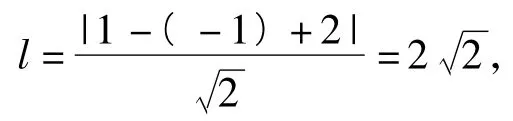
从而(a－c)2+(b－d)2的最小值为8.

例4已知正数a，b，c满足:5c－3a≤b≤4c－a，clnb≥a+clnc，则的取值范围是______.

解本题关键在于挖掘条件中多元不等式的内涵:5c－3a≤b≤4c－a，clnb≥a+clnc可化为

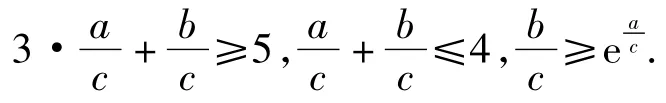
作出(x，y)所在平面区域(如图1).过原点作曲线y=ex的切线，设切点为P(t，et)，则

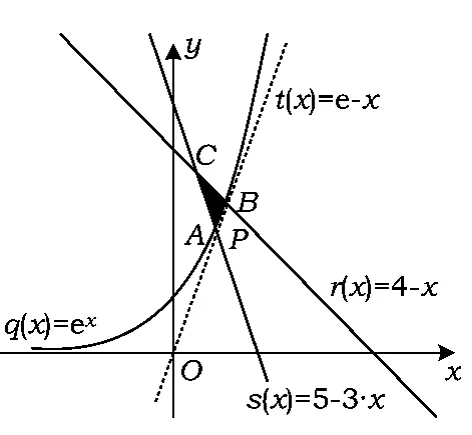
图1

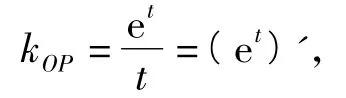
解得t=1，kOP=e.

点评在研究某些多元函数结构问题时，如果单纯从代数的角度去分析思考，往往很难找到正确的解题途径.这时若能根据函数式的结构特征，联想到与之相应的几何背景、几何模型，就可使问题迎刃而解，体现出简捷、明快、精巧、创新的数学风格.

5 分离提炼隐藏函数

有些多元方程f(x1，x2，…，xn)=0中，当取区间内的某一值时，相应地总有满足这一方程的唯一的xj(其中j∈{1，2，…，n})存在，那么多元方程f(x1，x2，…，xn)=0在该区间确定了一个隐藏函数xj=φ(xi)(其中i，j∈{1，2，…，n}(i≠j)).通过分离提炼隐藏函数xj=φ(xi)，从而实现问题的化解.但要注意有时隐藏函数xj=φ(xi)的确定显化是有困难的，甚至不可能的.

例5已知函数f(x)=x－aex(其中a∈R，x∈R).若函数y=f(x)有2个零点x1，x2，且x1＜x2.

1)求a的取值范围;

3)证明:x1+x2随着a的减小而增大.

(2014年天津市数学高考理科试题)

解1)由f(x)=x－aex，可得

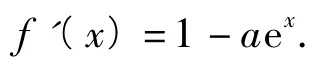
下面分2种情况讨论:

①当a≤0时，f'(x)＞0在R上恒成立，可得f(x)在R上单调递增，不合题意.

②当a＞0时，令f'(x)＞0得x＜－lna，令f'(x)＜0得x＞－lna.因此f(x)的单调递增区间是(－∞，－lna)，单调递减区间是(－lna，+∞).依题意得f(－lna)=－lna－1＞0，解得0＜a＜e－1，即a的取值范围是(0，e－1).

2)由x1－aex1=0得x1是自变量a的函数，2边关于a求导数得

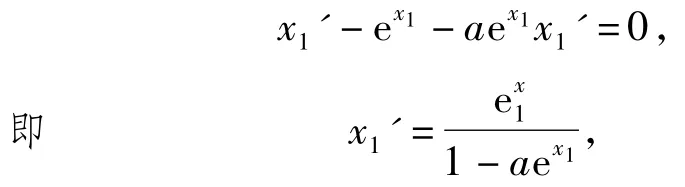
由第1)小题可知

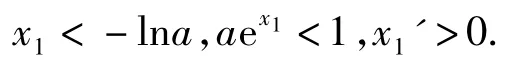
同理可得x2'＜0，即当自变量a的值减小时，x1的值减小，x2的值增大，从而(其中x1＞0，x2＞0)的值增大.

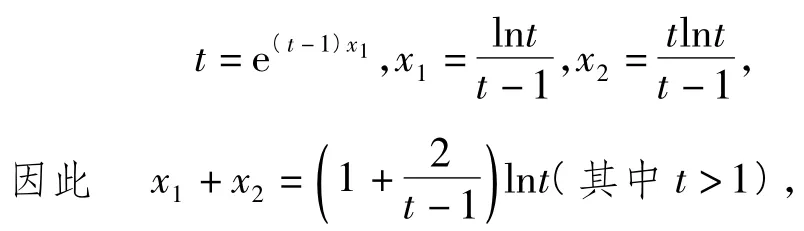
易知x1+x2在t∈(1，+∞)上随着t的增大而增大.而t随着a的减小而增大，故x1+x2随着a的减小而增大.

结束语多元函数结构的化解问题其实是个广泛而笼统的话题，在高中数学考查中屡屡涉及，着实让广大师生深感棘手茫然.但只要精心剖析多元结构式的本质特征或鲜明特点，巧妙灵活地通过换元、分离或提取等一系列措施，有效转化为一元函数问题解决，将一元函数的思想方法淋漓尽致地渗透或迁移在多元函数问题中，就能很好地解决，而这种处理方式也正符合高中数学新课程所提倡的高层次能力要求.