“立体几何中的度量计算”习题课教学设计

●任旭英(杭州市第九中学浙江杭州310020)

“立体几何中的度量计算”习题课教学设计

●任旭英(杭州市第九中学浙江杭州310020)

1 内容与内容解析

本节课是人教A版数学必修2第2章“空间点、直线、平面之间的位置关系”的一节习题课.

学生在直观认识和理解空间点、线、面位置关系的基础上，抽象出空间点、线、面位置关系的定义.并从上述定义、4个公理和1个定理出发，通过直观感知、操作确认、思辨论证，认识和理解空间中线面平行与垂直的判定与性质;能运用公理与定理证明空间位置关系的简单命题，从而掌握线线关系、线面关系、面面关系的联系.

内容解构:本节“立体几何的度量计算”的教学，以度量计算(异面直线所成的角、线面角、二面角、点到面的距离、几何体的体积)为问题，通过问题的解决(遵循“直观感知—操作确认—思辨论证—度量计算”的解决过程)梳理立体几何中的基础知识.

2 目标与目标解析

根据新课标的要求(培养和发展学生把握图形的能力、空间想象与几何直觉的能力、逻辑思维能力)以及本节的内容解构，本节习题课定位为:在新的情景中(立体几何的度量计算)，梳理已学习的内容，理解它们之间的内在联系.引导学生调整已有的认知结构，促进知识内化.从几何直觉到精准的计算，从直觉运用定理来证明命题到自觉地构建空间图形来计算，从而提升学生的空间想象能力和逻辑思维能力.具体地讲:通过错解分析，辨析核心概念，精确把握知识;通过多种解法分析，突显知识的内在联系，提高问题化归能力.

3 教学问题诊断

学生通过前面的学习，初步了解空间的点、线、面的位置关系.表现在每个学生对自己偏好的方法会反复应用，但一旦用这种方法解决不了或换个问题，就会束手无策.因此，如果没有把本章的内容串成线，织成网，学生就很难真正的理解与掌握.

本节课需要学生倾听同学的解法，抓住解法的关键.期盼学生能做精一道题，做通一类题.但很多学生往往掌握一种方法后，就不愿再继续听讲.因此应设法营造互相激励的氛围，发挥课堂上常用解法的优势，促进生生、师生之间的交流互动，达成对本章核心概念的深度理解.

4 教学过程设计

由易到难地呈现3个实例，把立体几何的度量问题串起来，深入地展示空间几何元素间的关系.先由学生自主思考，再通过错解、剖析概念、交流、展示解法，最后学生自行修正自己解题中的不足，拓宽解题思路，提高问题化归能力.

问题1如图1，在四棱锥P-ABCD中，PD⊥平面ABCD，PD=DC=BC=1，AB=2，AB∥DC，∠BCD= 90°.

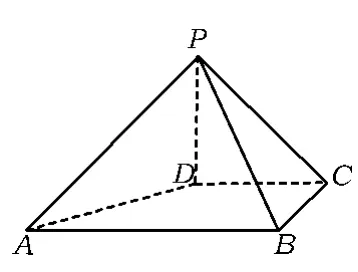
图1

1)求证:PC⊥BC;

2)求点A到平面PBC的距离.

设计意图题目简单，容易入手，每位学生都能动笔.知识内容上紧扣这章的重点(线线、线面和面面的位置关系)，但不同的入手角度，就会有不同的解题方法.在解题时可以通过点移、线移、面移来求解问题，能很好地训练学生把握图形的能力和空间想象能力;通过精确的计算，训练学生的逻辑思维能力.问题1不追求提炼解决问题的通解通法，旨在打开学生的思维，洞察知识间的联系.通过同伴对自己解法的评论，使学生提高元认知水平.

学生先行:学生独立完成第1)小题.

交流呈现:根据课堂情况，请学生板演自己的解法或通过实物投影展示学生的解法.

教师小结:归纳学生解题的角度，学生1和学生3通过计算得出BC与PC的位置关系;学生2通过线面垂直得到线线垂直.

学生先行:让学生独立完成第2)小题.

交流呈现:根据课堂情况，请学生板演自己的解法或通过实物投影展示学生的解法.

学生4:如图2，过点A作AH⊥PB于点H，AH的长即为所求.在△PBC中，，AB=2，，故

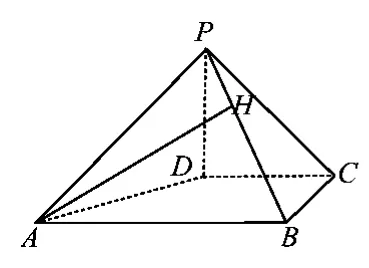
图2

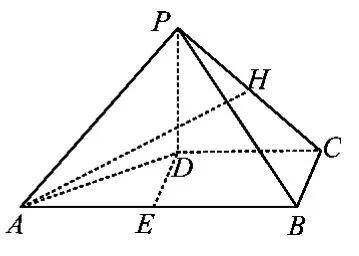
图3

学生5:如图3，取PC的中点H，易证DH⊥平面PBC，则点D到平面PBC的距离为DH的长，即为.过点D作DE∥BC交AB于点E，易证DE∥平面PBC，故点E到平面PBC的距离等于点D到平面PBC的距离，为.在梯形DCBA中，可知点E是AB的中点，故点A到平面PBC的距离是点E到平面PBC距离的2倍，即为

学生6:如图4，过点A作AE∥BC交CD的延长线于点E.又因为AE⊄平面PBC，所以AE∥平面PBC，故点A到平面PBC的距离等于点E到平面PBC的距离.易证PD=DC=ED，故EP⊥CP，易证BC⊥平面PEC，故PE⊥BC，解得PE⊥平面PBC，即PE的长为点E到平面PBC的距离.在△PEC中，，故点A到平面PBC的距离为

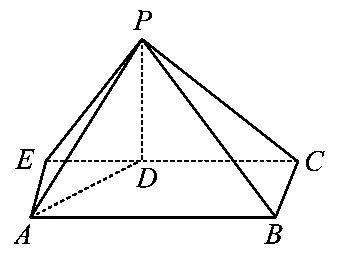
图4

图5

学生7:如图5，过点B作BE∥PC，过点A作AE⊥BE于点E，可证AE⊥平面PCBE，故AE的长即为所求.易证∠EBA=∠DCP=45°，在Rt△ABE中

学生8:等体积法:V三棱锥A-PBC=V三棱锥P-ABC，点P到平面ABC的距离即为PD的长，可以求得点A到平面PBC的距离为

交流学习:学生4的解法为错解，AH⊥PB，AH不一定垂直平面PBC.若AH⊥平面PBC，则AH⊥CB.又因为CB⊥AB，所以CB⊥平面ABP，故CB⊥PB.在△PBC中，∠PBC+∠PCB=180°，这与三角形的内角和为180°矛盾.上述解法中等体积法最为容易.

教师小结:各解法的关键是寻找平面PBC的垂线，根据面面垂直的性质定理，可以在平面PBC的垂面上寻找垂线，易知平面DPC⊥平面PBC，在平面DPC内作公共棱的垂线，即学生5的解法.把点A平移到平面DPC内，易作平面PBC的垂线，即学生6的解法.把垂面PDC平移到平面ABE，即学生7的解法.当我们把握解题的关键时，不同的角度就会有不同的解法，同时不同的解法也帮助我们理解问题的关键，从而理解知识是如何联结的.

问题2在直棱柱ABC-A1B1C1中，∠ABC=90°，AB=BC=AA1=a，点O1是A1C1的中点.

1)求A1B与B1O1的夹角大小;

2)求A1B与平面A1ACC1所成角的大小;

图6

3)求B1O1与平面B1AC所成角的正弦值.

设计意图学生间对问题1交流的成果，要内化为每个个体自身的独特体验，需要重复的训练.第1)小题让学生体验前面的交流成果，使学生有一些成就感，激发他们积极参与课堂活动.后2个小题是求线面角.

学生先行:独立完成第1)小题.

交流呈现:展示学生的解法.

学生1:如图7，取AC的中点O，联结BO，OO1，可证四边形B1O1OB为平行四边形，则B1O1∥ BO，故∠A1BO就是所求的角.在△A1BO中，，从而∠A1BO=60°.

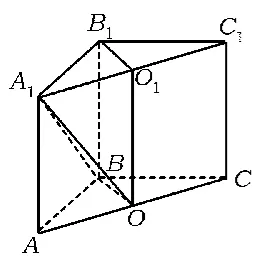
图7

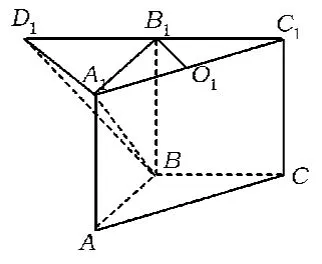
图8

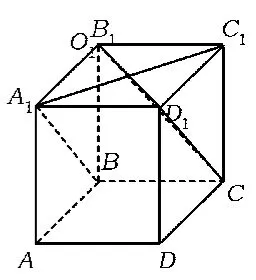
图9

学生2:如图8，倍长C1B1至点D1，联结A1D1，BD1，易证∠D1A1B就是所求的角.在△D1A1B中，，从而∠D1A1B=60°.

学生3:根据题目的条件，直三棱柱可以补全为正方体，如图9，可得∠CD1B1=60°.

学生4:向量法也可行的.

故异面直线BA1，B1O1所成的角为60°.

学生先行:呈现学生的解法.

学生1:如图10，易证BO⊥平面A1ACC1，故∠B1AO就是BA1与平面A1ACC1所成的角.在直角△B1AO中，∠B1AO=30°.

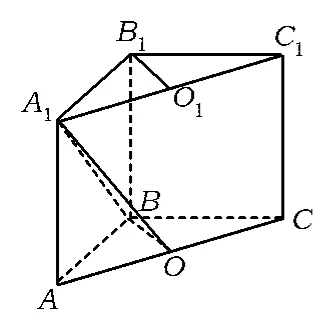
图10

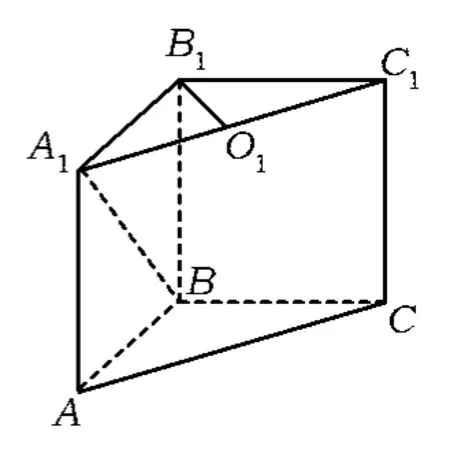
图11

学生2:如图11，根据题意容易得到，点B1到平面A1ACC1距离为B1O1，即为.而B1B∥平面A1ACC1，故点B到平面A1ACC1距离为，从而

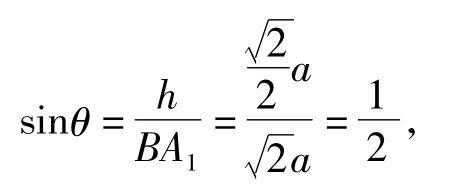
于是BA1与平面A1ACC1所成的角为30°.

教师小结:找线面角的关键是找平面的垂线，转化为线线角(直线与投影线的交角或直线与面的垂线交角的余角);学生2的方法也不错，也是找出面的垂线，从而求点到面的距离.

学生呈现:独立思考.根据课堂情况，请学生板演自己的解法或通过实物投影展示学生的解法.学生也会根据黑板上的解法，不断修正自己的解法.

学生1:如图12，通过等积法求得点A1到平面B1AC的距离为，可证A1O1∥平面B1AC，故点O1到平面B1AC的距离也为，从而

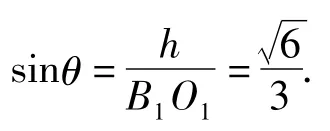
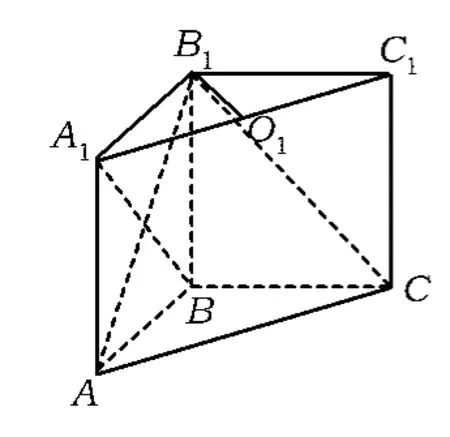
图12

图13

学生2:如图13，补形成正方体，可证D1B⊥平面B1AC，垂足难定，但∠B1D1B是所求角的余角，于是

学生3:如图14，方法类似于学生2，垂足可求，垂足在平面B1BDD1与平面B1AC的交线B1O上，即B1O与D1B的交点H.在直角△B1D1H中可求得∠D1B1H.

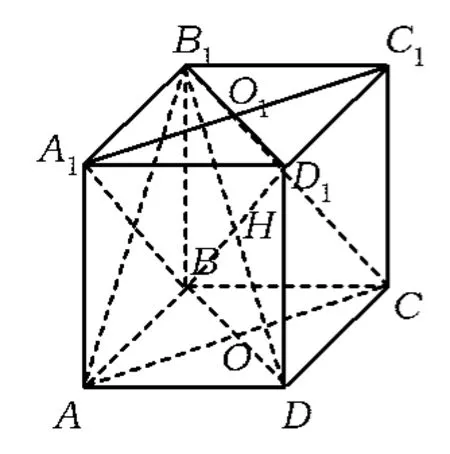
图14

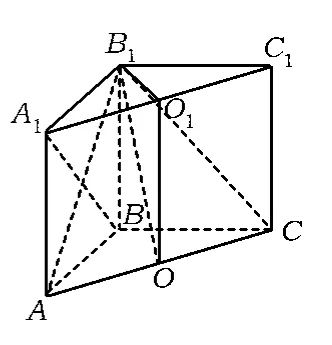
图15

学生4:如图15，易证AC⊥平面B1O1OB，则平面B1AC⊥平面B1O1OB，平面B1AC与平面B1O1OB的交线即为直线B1O1在平面B1AC的投影，故∠O1B1O就是线面角.在直角△O1B1O中可求得∠D1B1H.

教师小结:通过计算的方法求线面角，或根据线面角的定义，通过构图的方法求解，先找平面的垂线，再在斜线与投影线所确定的直角三角形中求解，或者寻找经过斜线且与平面垂直的垂面上求线面角的大小.求线面角的关键是找平面的垂线，然后转化为斜线与投影线的角或斜线与垂线所成角的余角.

问题3如图16，正三棱柱ABC-A1B1C1的所有棱长都为2，D为CC1中点.

1)判断AB1是否垂直于平面A1BD，若AB1⊥平面A1BD，请证明之，反之求直线AB1与平面A1BD所成的角;

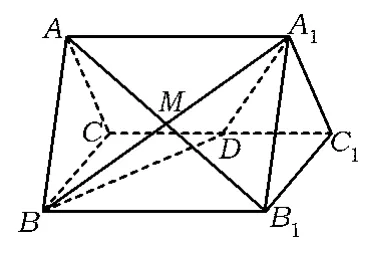
图16

2)求二面角A-A1D-B的正弦值.

设计意图使学生经历“直观感知—思辨论证—度量计算”的认识过程，熟练掌握线面垂直的判定，理解线面垂直的判定转化线线垂直的判定.会求特殊条件下的二面角的平面角，并借此理解已学内容间的逻辑关系，提高学生的逻辑思维能力.

学生先行:根据课堂情况，请学生板演自己的解法或通过实物投影展示学生的解法.

交流呈现:

学生1:如图17，易证DA=DB1，而AM=MB，故DM⊥AB1，又AA1B1B是正方形，故A1B⊥AB1，从而AB1⊥平面A1BD.

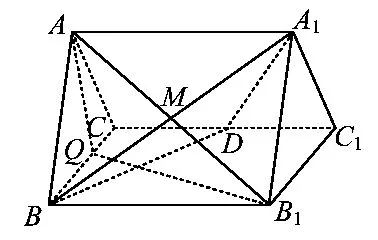
图17

图18

学生2:取BC的中点Q，联结AQ，B1Q.在侧面BB1C1C中可证B1Q⊥BD，AQ⊥BD，故BD⊥平面AQB1，从而BD⊥AB1.又因为A1B⊥AB1，所以AB1⊥平面A1BD.

故BD⊥AB1.又因为A1B⊥AB1，所以AB1⊥平面A1BD.

教师小结:线面垂直的判定转化为线线垂直的判定，从而空间问题转化为平面问题.

交流呈现:根据课堂情况，请学生板演自己的解法或通过实物投影展示学生的解法.

学生4:需要找公共棱A1D的垂面，由第1)小题的结论可知A1D⊥AB1，故在平面AA1D内作AH⊥A1D于点H(如图19)，则A1D⊥平面AHM，故∠AHM就是所求的角.在直角△AMH中，

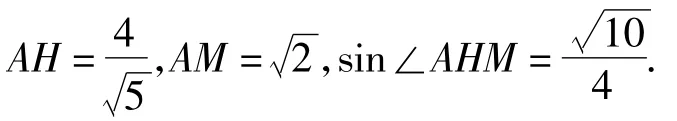
图19

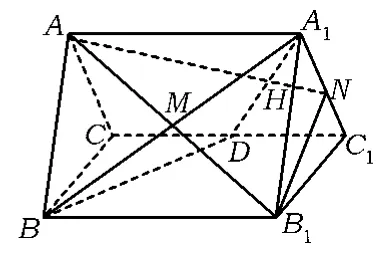
图20

学生5:在二面角的平面AA1D内作公共棱A1D的垂线AH，AH与平面A1DB的角就是二面角的平面角.与学生4的解法类似，只是作辅助线出发点不同.

学生6:取A1C1的中点N，可知B1N⊥平面AA1D，故A1D⊥B1N.又因为AB1⊥平面A1BD，所以A1D⊥AB1，故A1D⊥平面ANB1，垂面ANB1分别交平面AA1D和平面BA1D于AH，MH，则∠AHM就是所求的角.与学生4的解法如出一辙.

教师小结:引导学生观察学生6的解法，理清垂线AB1与NB1的夹角与二面角的平面角的关系.

学生完成后，教师小结要点:

1)找二面角的平面角可以寻找公共棱的垂面或公共棱的垂线;

2)找二面角的2个半平面的垂线，垂线的夹角跟二面角的平面角相等或互补;

3)二面角的平面角也可以转化为求一个半平面内与公共棱垂直相交的直线与另一个半平面所成的角.

学生给前面的3个点配上对应的空间立体图形.把枯燥的文字表达转化为简洁的图形叙述.

问题4请整理本节课的所得.

设计意图概括、归纳本节课的所得，获取简洁、一般、通用的思路与方法.

教师回答要点:1)通过综合或分析法，依据立体几何中的定义、公理、定理，把立体几何问题转化为平面几何问题;

2)把立体几何的有关计算问题转化为向量的计算问题，向量的计算过程也是把立体几何问题转化为平面几何问题的过程.

5 布置作业

1.直角△ABC的斜边在平面α内，2条直角边分别与平面成30°和45°，求这个直角三角形所在平面与平面α所成的二面角的大小.

2.在三棱锥P-ABC中，侧梭长均为4，底边AC=4.AB=2，BC=2，D，E分别为PC，BC的中点.

1)求证:平面PAC⊥平面ABC;

2)求三棱锥P-ABC的体积;

3)求二面角C-AD-E的余弦值.

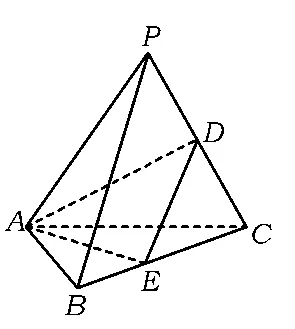
图21

［1］李学军.“习得”型习题课及其教学设计［J］.中小学数学:高中版，2014(1):26-27.

［2］王红权.“平面向量”习题课设计［J］.中小学数学:高中版，2014(2):7-10.