对求整边三角形个数的一点思考

●金竹明(洛舍镇中心学校浙江德清313218)

对求整边三角形个数的一点思考

●金竹明(洛舍镇中心学校浙江德清313218)

在初中数学教学过程中，我们经常会碰到已知三角形周长，求边长为整数的三角形个数或求三角形的各边长度等问题.对于这样的问题，我们可以用穷举法将所有的情况全部列出，然后利用“三角形两边之和大于第三边”排除不符合要求的“三角形”，进而得到正确的结果.显然求解过程比较繁琐，费时费力，稍有不慎，可能功亏一篑.对于这种类型的问题，笔者进行了一番思考、分析，得出了一种可简化“排除法”过程的方法，以期在今后的教学过程中对教师有所裨益.以下为了叙述方便，我们将边长为整数的三角形称为整边三角形.

例1在平面内，分别用3根、5根、6根火柴棒首尾顺次相接搭三角形，多少根火柴棒能搭成等腰三角形?等边三角形呢?通过尝试，完成表1.那么7根火柴棒呢?8根呢?9根呢?你发现了什么规律?

表1 火柴棒能搭成的三角形

(浙江教育出版社《数学》八年级上册第25页“探究活动”)

分析此题要求我们思考、解决的是火柴棒根数为6，7，8，9时围成的等腰三角形、等边三角形的个数情况.本题不难解决.

例2用6根火柴摆三角形(恰好有6根)，只能摆一个.设每根火柴的长度均为1，则所摆三角形的边长均为2.用7根火柴摆三角形，能摆出2种情况:3条边长分别为1，3，3，或者分别为2，2，3.

1)用8根火柴能摆出几种不同的情况?

2)用10根火柴能摆出几种不同的情况?

3)若摆出来的三角形周长为17，那么满足条件的三角形有多少个?

这是《单元目标达成测试卷》八年级上册数学(五)期中复习的第24题.题目要求我们解决的是周长确定的整边三角形的个数问题.显然在本题中周长的数据比较小，解决也不是很困难.但很明显的一个延伸、拓展问题就是“周长确定的整边三角形的个数该如何确定?方法怎样?”这个问题就比较复杂，有一定难度.

例3求周长为12的整边三角形的所有可能情况.

分析拿到此题，初看可能会感觉无从下手.仔细思考，可能会有如下的解题思路:不妨设三角形的3条边长分别为a，b，c，且a≤b≤c.记(a，b，c)为一种情况，显然a≥1且a为正整数，可得(1，1，10)，(1，2，9)，(1，3，8)，(1，4，7)，(1，5，6);(2，2，8)，(2，3，7)，(2，4，6)，(2，5，5);(3，3，6)，(3，4，5);(4，4，4)这12种情况，然后我们可以由“三角形两边之和大于第三边”(其实只要考虑“最小两线段之和大于最长线段”这一种情况即可)去排除不能构成三角形的情况:(1，1，10)，(1，2，9)，(1，3，8)，(1，4，7)，(1，5，6);(2，2，8)，(2，3，7)，(2，4，6);(3，3，6).最后可得周长为12的整边三角形只有(2，5，5)，(3，4，5)，(4，4，4)这3种情况.虽然此方法可解决这一类问题，但显然三角形的周长越大，所需考虑、排除的情形也越多，分析解决问题所需的时间也越长.我们希望此类问题能有更简单的方法.

下面考虑一般问题:

例3已知:△ABC的周长为l，边长分别为a，b，c，其中a≤b≤c，求△ABC中最长边c的取值范围.

分析由题意，得a+b+c=l，因为

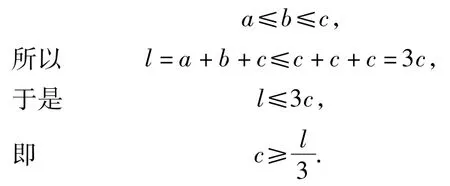
又因为三角形两边之和大于第三边，所以

综合以上分析，有如下的结论:若△ABC的周长为l，3条边长分别为a，b，c，且a≤b≤c，则三角形中最长边c的取值范围是由此，我们可以比较简单地确定周长为定值的整边三角形的个数.

接下来利用上述结论再来解决例2:

分析先根据上述结论确定最长边c的取值范围，然后再由b≤c来确定b，最后由周长及a≤b来确定a即可，过程要比单纯的穷举法简便不少.

解不妨设三角形的3条边长分别为a，b，c，且a≤b≤c，记(a，b，c)为一种情况.因为

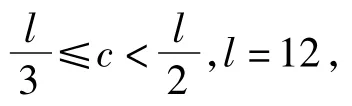
又c为正整数，得c=4或c=5.

1)当c=4时，有(a，b，4)符合要求.因为b≤c，c=4，所以b≤4.

①当b=4时，由a+b+c=12得a=4，符合要求;

②当b=3时，由a+b+c=12得a=5，不符合a≤b≤c的假设，舍去.

③当b≤2时，a≥6，不符合a≤b≤c的假设，舍去.

2)当c=5时，有(a，b，5)符合要求.因为b≤c，c=5，所以b≤5.

①当b=5时，由a+b+c=12得a=2，符合要求;

②当b=4时，由a+b+c=12得a=3，符合要求;

③当b=3时，由a+b+c=12得a=4，不符合a≤b≤c的假设，舍去;

④当b≤2时，a≥7，不符合a≤b≤c的假设，舍去.

综合以上，周长为12的整边三角形只有(4，4，4)，(2，5，5)，(3，4，5)这3种情况.

事实上，当取到a＞b时，后面的情况都不需要考虑了.这样我们真正需要考虑的情况就大大减少，解决问题所需要的时间也就相应减少.

例4将长度为2n(n为自然数，且n≥4)的一根铅丝折成各边长均为整数的三角形.记(a，b，c)为边长为a，b，c且满足a≤b≤c的一个三角形.

1)就n=4，5，6的情况，分别写出所有满足题意的(a，b，c).

2)有人根据第1)小题的结论，猜想:当铅丝的长度为2n(n为自然数，且n≥4)时对应(a，b，c)的个数一定是n－3.事实上这是一个不正确的猜想.请写出n=12时所有的(a，b，c)，并回答(a，b，c)的个数.

3)试将当n=12时所有满足题意的(a，b，c)按照至少2种不同的标准进行分类.

(浙江教育出版社《数学竞赛阶梯训练》第2册八年级第148页第13题)

分析在本题中，显然整边三角形的周长l= 2n.对于第1)小题:当n=4时，l=8，由，容易确定，由c为正整数，得c=3.当b=3时，a=2;当b=2时，a=3，不合要求，舍去.因此当n=4时，整边三角形只有(2，3，3)这1种情况.当n=5，6时，方法类似.

对于第3)小题，与整边三角形的个数问题关系不大，不再赘述.

我们再去思考例1中整边等腰三角形的个数问题.虽然我们在确定整边三角形个数后，只要再检验a，b，c中是否有2个或3个值相等即可得到周长确定的整边等腰三角形，但是否有更简洁的方法呢?

设等腰三角形的腰长为m，底边长为p，周长为l，则l=2m+p.因为

又l=2m+p，2m为偶数，知l与p奇偶性相同，即当等腰三角形的周长l为奇数时，其底边p只需考虑的奇数;当等腰三角形的周长l为偶数时，其底边p只需考虑的偶数.

显然一个p的值对应一个等腰三角形，因此p的值一旦确定后，整边等腰三角形的个数也就可以确定了.

例5求周长分别为12，15的整边等腰三角形的个数.

分析由上述结论可知整边等腰三角形的个数取决于底边p的取值.整边等腰三角形的底边p满足，且p与l的奇偶性相同:①当整边等腰三角形的周长l=12时，有，即0＜ p＜6.又p与l的奇偶性相同，且l=12为偶数，因此p为偶数，则p=2或p=4，腰长或 4.故周长为12的整边等腰三角形有2个:(5，5，2)，(4，4，4).②当整边等腰三角形的周长l=15时，有又p与l的奇偶性相同，且l=15为奇数，因此p为奇数，则p=1，3，5或7，腰长，6，5或4.故周长为15的整边等腰三角形有4个:(7，7，1)，(6，6，3)，(5，5，5)，(4，4，7).

事实上，周长为l(l是自然数，且l≥3)的不同整边三角形的个数T满足表2的关系(其中k为自然数):

表2 周长为l的不同的整边三角形的个数

这个结论的推导过程比较复杂，也比较困难，因此不在这里说明.

［1］章建民.周长为定值的整边三角形的个数问题［J］.中学数学，1996(12):24-25.