看似崎岖最寻常成如艰辛却容易——数列中一类不定方程通解探秘

●孙小龙(如皋市第一中学江苏如皋226500)

看似崎岖最寻常成如艰辛却容易
——数列中一类不定方程通解探秘

●孙小龙(如皋市第一中学江苏如皋226500)

1 问题呈现

例1各项均为正数的数列{an}中，设Sn= a1+a2+…+an，，且(2－ Sn)(1+Tn)=2，n∈N*.

1)设bn=2－Sn，证明:数列{bn}是等比数列;

(2014年江苏省南通市三模试题第20题)

1)略.

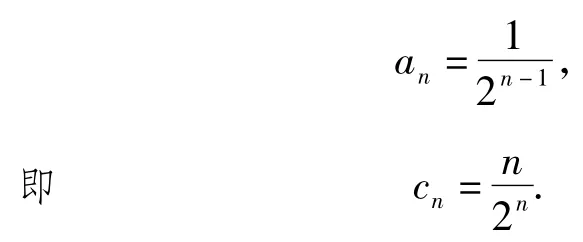
由cm+cr=2ck，得

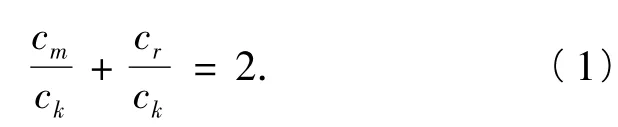
①当m≥2时，若k－m≥2，则

此时式(1)不成立，故k－m=1，即k=m+1.令r= m+1+i(其中i∈N*)，则

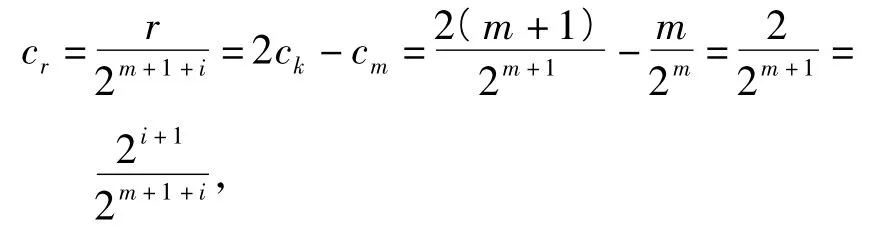
因此r=2i+1，即存在满足题设的数组{(2i+1－i－1，2i+1－i，2i+1)}(i∈N*).

②当m=1时，若k=2，则r不存在;若k=3，则r=4;若k≥4，则，式(1)不成立.

综上所述，所求集合为{(1，3，4)，(2i+1－i－1，2i+1－i，2i+1)}(其中i∈N*).

学生普遍反映:第2)小题较难，方程中含有3个字母，具有很多的不确定性，没有明确的思路和化简方向，无从下手，只能选择放弃.甚至有些教师评讲时也觉得无从下手，认为参考答案看得懂却想不到，尤其是与平时同类试题的解题方法有很大不同，于是也选择了放弃.是否果真如此?让我们从常见的同类试题的解题方法中来分析、探秘、追寻答案.

2 旧题反思

例2设m，n，p∈N*，m＜n＜p，an=2n，问:数列{an}中是否存在3项am，an，ap，使数列am，an，ap是等差数列?如果存在，求出这3项;如果不存在，说明理由.

解假设存在3项am，an，ap，使数列am，an，ap是等差数列，可得

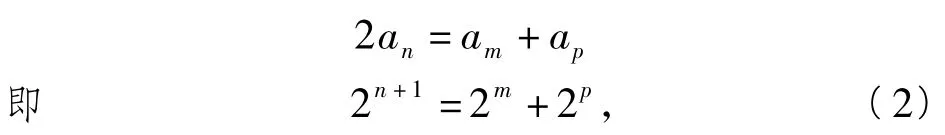
等式2边同除以2m可得

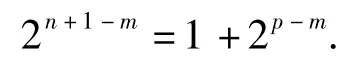
因为n+1－m∈N，p－m∈N*，所以2n+1－m为偶数，而1+2p－m为奇数，式(2)不成立，故不存在3项am，an，ap成等差数列.

点评本题是数列中不定方程求解的典型试题.上述解法是解决此题最常用的方法，也是学生和教师解题时的首选方法.这种方法是根据题中数字特点加以巧妙判断，但局限性较大，数字稍作变动，就行不通了.因此，此种方法虽妙，但不是通性通法，无法进行推广与平移.笔者经研究发现此题的解法有很多，大同小异，但有一种解法与众不同.

另解假设存在3项am，an，ap，使数列am，an，ap是等差数列，可得

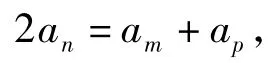
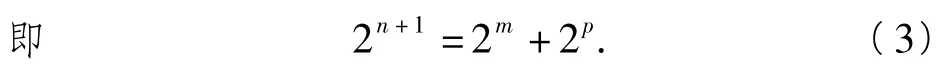
由于p＞n，即p≥n+1，从而2p≥2n+1，又2m＞0，得

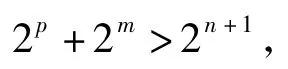
因此式(3)不成立，故不存在3项am，an，ap成等差数列.

点评“另解”根据2个不等的正整数之间至少相差1的特点，利用等式右边较大的一项，对等式2边的大小作了比较.这种方法思路清晰，层次分明.是否具有一般性?可否推广?能否合理迁移?下面让我们用试题来检验.

3 牛刀小试

例3设m，n，p∈N*，m＜n＜p，，问:数列{an}中是否存在3项am，an，ap，使数列am，an，ap是等差数列?如果存在，求出这3项;如果不存在，说明理由.

解假设存在3项am，an，ap，使数列am，an，ap是等差数列，可得

因为m＜n，即m≤n－1，所以

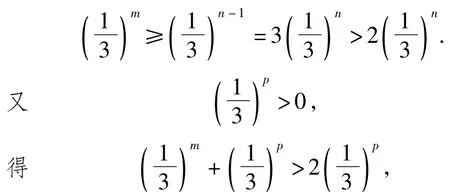
从而式(4)不成立，故不存在3项am，an，ap成等差数列.

例4设m，n，p∈N*，m＜n＜p，，问:数列{an}中是否存在3项am，an，ap，使数列am，an，ap是等差数列?如果存在，求出这3项;如果不存在，说明理由.

解假设存在3项am，an，ap，使数列am，an，ap是等差数列，可得2an=am+ap，即

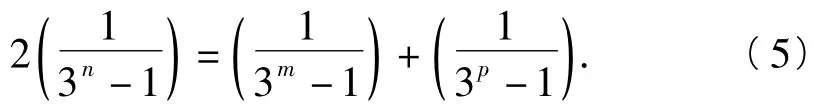
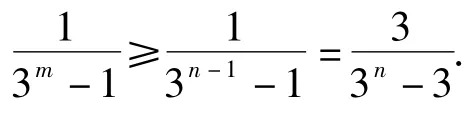
从而式(5)式不成立，即不存在3项am，an，ap成等差数列.

点评例3、例4中运用上述方法能够快速准确地突破难点、解决问题，进一步说明例2中的“另解”具有推广价值，方法具有一般性.

4 提炼完善

例5设m，n，p∈N*，m＜n＜p，，问:数列{an}中是否存在3项am，an，ap，使数列am，an，ap是等差数列?如果存在，求出这3项;如果不存在，说明理由.

解假设存在3项am，an，ap，使数列am，an，ap是等差数列，可得

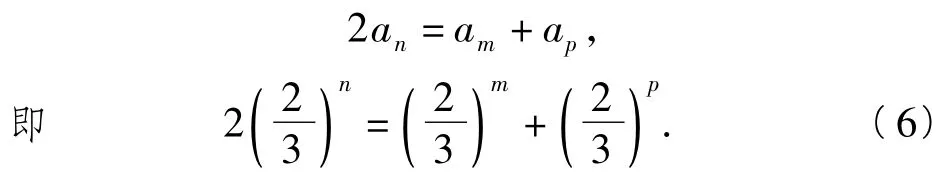
由于m＜n，即m≤n－1.

1)若m≤n－2，则

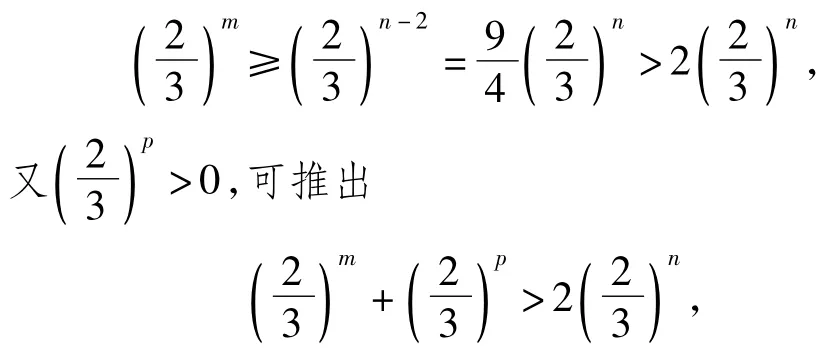
故式(6)不成立;

2)若m=n－1，则式(6)可化为

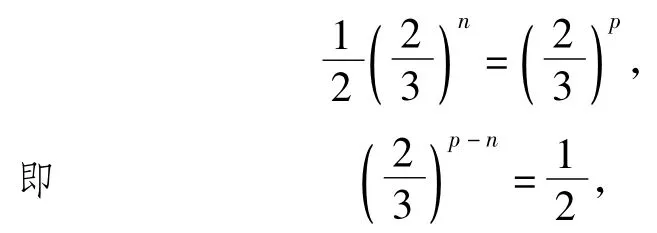
可知此式无解.

综上所述，不存在3项am，an，ap成等差数列.

例6设m，n，p∈N*，m＜n＜p，，问:数列{an}中是否存在3项am，an，ap，使数列am，an，ap是等差数列?如果存在，求出这3项;如果不存在，说明理由.

解假设存在3项am，an，ap，使数列am，an，ap是等差数列，可得

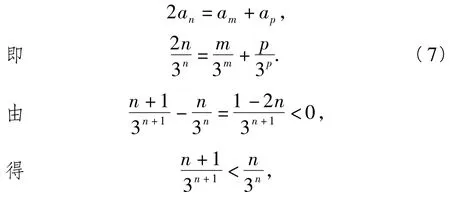
从而式(7)不成立.

综上所述，存在3项a1，a2，a3成等差数列.

点评1)若利用2个不相等的正整数之间至少相差1不能解决问题，则可将2个不等的正整数之间的差合理扩大，直至等式不成立，从而使等式成立的2个不等的正整数之差只有有限种可能，再一一列举解决.

2)若利用2个不相等的正整数之间至少相差1解决问题时，受到其中一个字母范围的影响，则可将此字母的范围合理扩大，直至等式不成立，从而使等式成立的该字母的取值只有有限种可能，再一一列举解决.

5 考题再现

有了上面解题方法的提炼完善，笔者对本文例1第2)小题重新解答如下:

解2)由第1)小题知

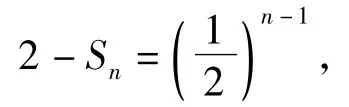
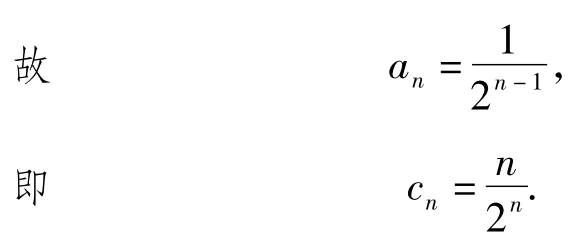
由cm+cr=2ck可得

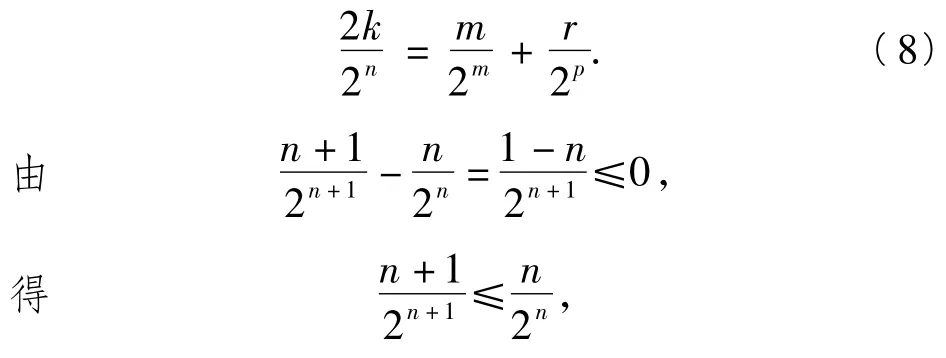
②若m=k－1，等式(8)可化为

由于r＞k，令r=k+i(其中i∈N+)，代入式(9)可得k=2i+1－i，从而r=2i+1，m=2i+1－i－1，故存在满足题意的数组{(2i+1－i－1，2i+1－i，2i+1)}(其中i∈N+).

综上所述，所求集合为{(1，3，4)，(2i+1－i－1，2i+1－i，2i+1)}(其中i∈N*).

点评再次对照可以发现，参考答案所用的方法其实与上面提炼完善的通性通法是一致的，只不过处理的手段不同而已.真是“看似崎岖最寻常，成如艰辛却容易”.

6 感悟至深

“通性通法”是解决某类问题的基本方法，具有普遍的指导意义，能揭示一类问题本质，反映其内在联系，能够在一类问题中进行迁移与推广.教师在数学解题教学中要仔细分辨，淡化抓住题目“个性”特质的专用方法，要尽量挖掘解决问题最本质、最基本的方法，即要提倡和重视“通性通法”，这样也易于消除多数学生对数学的恐惧心理，增强学生学好数学的信心.如果主次颠倒，那么学生看到题目时，首先考虑的不是通性通法，解题一旦遇阻，就毫无章法，甚至无从下手，不能从容得分.从近几年数学高考试题中可以看出，高考重视对基础知识、基本技能和通性通法的考查，最大程度地遏制了特殊技巧生存的空间，对高中数学教学起到了很好的导向作用.