2014年安徽省中考压轴题的解法探究、思考、追寻与推广

●韩敬 唐家周 谢宗彬(定远县第一初级中学安徽定远233200)

2014年安徽省中考压轴题的解法探究、思考、追寻与推广

●韩敬 唐家周 谢宗彬(定远县第一初级中学安徽定远233200)

中考试题对教学具有导向性，研究中考试题对教学有着重要的指导意义，多角度对中考试卷压轴题的研究，能挖掘其内涵，追寻命题者的足迹，既有意义，也有价值，为今后的教学指明方向.

1 试题呈现与解析

题目如图1，正六边形ABCDEF的边长为a，P是BC边上一动点，过点P作PM∥AB交AF于点M，作PN∥CD交DE于点N.

1)①求∠MPN;②求证:PM+PN=3a.

2)如图2，点O是AD的中点，联结OM，ON，求证:OM=ON.

3)如图3，点O是AD的中点，OG平分∠MON，判断四边形OMGN是否为特殊四边形?并说明理由.

(2014年安徽省数学中考试题第23题)

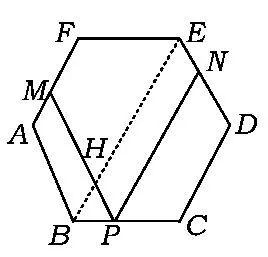
图1

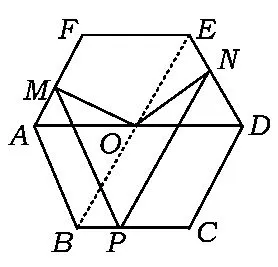
图2

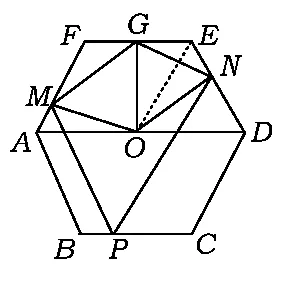
图3

分析1)①易知∠MPN=180°－∠BPM－∠NPC=180°－60°－60°=60°.

②联结BE交MP于点H(如图1).在正六边形ABCDEF中，因为PN∥CD，又BE∥CD∥AF，所以BE∥PN∥AF.又因为PM∥AB，所以四边形AMHB，HENP均为平行四边形，且△BPH是等边三角形，从而

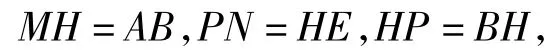
于是PM+PN=MH+HP+PN=AB+BH+HE= AB+BE=a+2a=3a.

图4

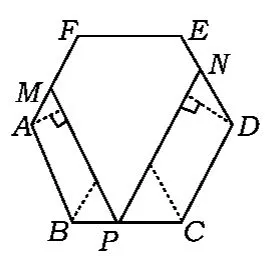
图5

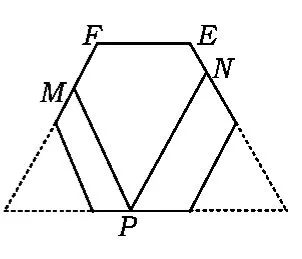
图6

点评此问第①小题主要考查正多边形相关知识、平行线的性质、平角定义等基本知识点;第②小题实际上考查了等腰梯形的相关知识.解决梯形的基本方法有作高线构成双直角三角形与矩形(如图4)、作腰平行线构成平行四边形与三角形(如图5)、延长2条腰构造三角形(如图6).当识别出等腰梯形时，自然会想到这些解法，此问尊重了学生的个性，真正把“不同的人在数学上得到不同的发展”的理念融入考题之中.

2)解法1如图2，联结OE，因为PC=DN，所以BP=EN，又BP=AM，得AM=EN.因为∠MAO=∠NEO=60°，OA=OE，可得△OMA≌△ONE，所以OM=ON.

解法2如图7，因为正六边形是轴对称图形，且对称轴是过正六边形中心与边垂直的直线，所以可过点O作AB的垂线OG，与AB交于点G，可知OG是AB的中垂线.易知四边形ABPM是等腰梯形，从而OG也是PM的中垂线，可得OM=OP，同理可得ON=OP，故OM=ON.

图7

点评此问考查的是全等模型思想.所证结论已暗示我们可以从三角形全等角度来考虑，尝试找OM，ON这2条线段所在的2个三角形全等，联结OE或OF都能构造出全等三角形，这是第一种方法.除此之外，还可以考虑用垂直平分线定理来证，于是便有了文中的解法2.“求出解答并继续前进”(舍费尔德语)，从这一解法可知点P，M，N在以O为圆心的圆上，由圆周角定理得∠MON= 2∠MPN=120°.从圆的角度来考虑，轻松突破解决第3)小题中所需的“∠MON=120°”这一关键角度.新课标修订中突出强调了数学抽象的思想、推理的思想、模型的思想这3种基本思想，此问是全等模型思想的运用，体现了四基之“基本思想”.

3)解法1如图3，联结OE，由第2)小题得△OMA≌△ONE，于是∠MOA=∠EON，易知EF∥AO，且EF=AO(正六边形的边长等于半径)，故四边形AOEF是平行四边形，从而

解法2联结OE，OP(如图8)，由第2)小题知OM=ON= OP，可知点P，M，N在以O为圆心的同一圆上，从而

∠MON=2∠MPN=120°，下同解法1(略).

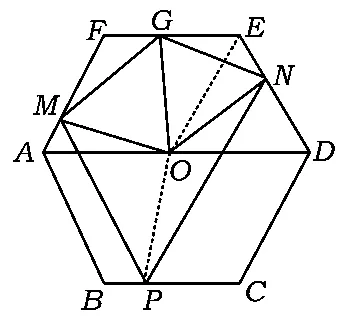
图8

点评此问考查了平行四边形、三角形全等、等边三角形、菱形等相关知识，突出考查新课标中倡导的“猜想与验证”能力.此问难度大，拉开了学生的档次，从抽样统计的结果来看，这一问得分率极低，达到了选拔的目的.

此问难在哪里?从解法1可以发现:难在“∠MON=120°”的确定，学生完全能猜出是菱形，但不知道如何验证.这里可作如下思考:假如四边形OMGN是菱形，就有OM=MG=GN=ON，将动点P移至点B位置时，可知点M与点A重合、点N与点E重合，由正六边形半径与边长相等，可知OM(OA)=GN=EF，从而点G与点F重合，此时易知AOEF是平行四边形，而∠F=120°，根据平行四边形对角相等，可得∠MON=120°，关键角度突破，问题得证.该思路告诉我们:在遇到动点问题时，将动点移至特殊位置，往往就能找到解题路径.这就是波利亚《怎样解题》中第2步(拟定计划)环节里所说的“先解决一个特例试试”.也就是说学生解答不好或无从下手的原因是缺少解答这类问题的方法与经验.解法2从圆的角度来思考，“∠MON=120°”来得虽容易，但它依赖于第2)小题中解法2的反思“成果”，没有该“成果”，这种解法就难以出现.这一问将几何直观与猜想、验证进行了很好的融合，是一大亮点.

2 思考与追寻

著名的教学教育家波利亚曾形象地指出:“好问题同某种蘑菇有些相像，它们都成堆地生长，找到一个以后，你应当在周围找找，很可能附近就有好几个.”我们再来探索在第2)小题的条件下，当点P在BC上时，△AOM与△DON面积之间有何关系?五边形MONEF面积是变还是不变?

如图9，联结OE，OF，则

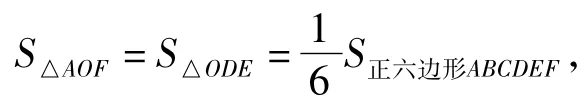
由第2)小题的解法知

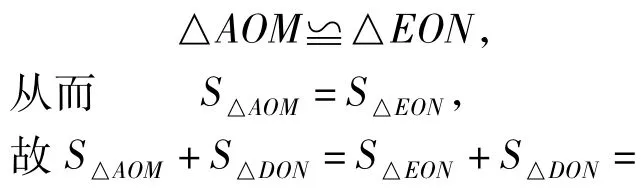
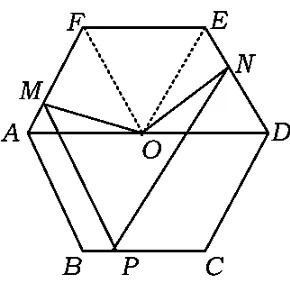
图9

由此得结论:点P在运动过程中，△AOM与△DON面积之和总等于原正六边形面积的，五边形MONEF的面积总等于原正六边形面积的也就说，△AOM与△DON面积之和、五边形MONEF的面积都是定值.

由第3)小题的解法知∠MON=120°，结合第2)小题的结论OM=ON，易构造出如图10所示的一个模型，也就是构造一个与正六边形ABCDEF全等的正六边形A'B'C'D'E'O，使它绕正六边形ABCDEF的中心O旋转，这样题中的由点P的运动而带动的点M、点N运动就可以看成正六边形A'B'C'D'E'O绕点O旋转的特例.显然，此时OM= ON始终不变，五边形MONEF的面积也不变.

当构造出这样的模型时，容易让我们联想到常见的一道题:如图11所示，已知正方形ABCD的对角线交于点O，O是正方形A'B'C'O的1个顶点，2个正方形的边长都为a(可变量).若正方形A'B'C'O绕点O任意转动.1)求证:OE=OF;2)试求重叠部分OEBF的面积.

(结论:OE=OF且重叠部分OEBF的面积总等于正方形ABCD面积的.)

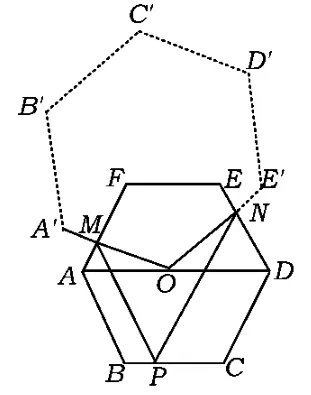
图10

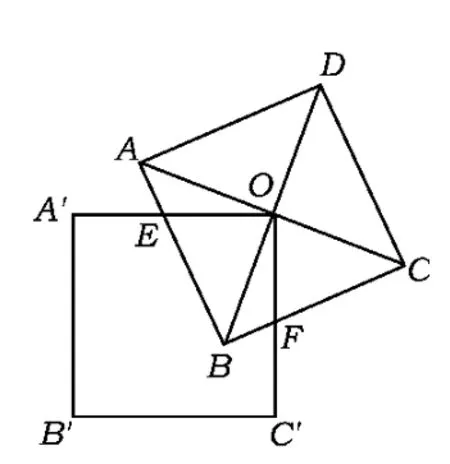
图11

显然，从形式上来探索，就能推广到一般.即有2个相似正n边形，若较大的正n边形顶点置于较小的1个正n边形的中心，绕其中心旋转，那么重叠部分的面积始终不变.

探究至此，笔者大胆追寻命题者的足迹:这道大家熟悉的正方形问题也许就是这道压轴题的“母题”.不管笔者的猜测正确与否，都将启示我们要重视对试题的拓展教学.

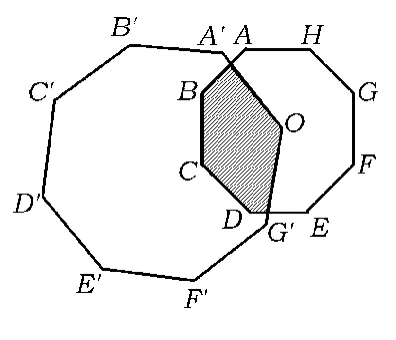
图12

由上面的经验，还可编制类似的模拟试题，如:

如图12，已知正八边形ABCDEFGH与正八边形A'B'C'D'E'F'G'O，O是正八边形ABCDEFGH的中心，把正八边形A'B'C'D'E'F'G'O绕点O任意转动，那么重叠部分(阴影部分)的面积与正八边形ABCDEFGH的面积有何关系?说明你的理由.

(结论:重叠部分的面积总等于正八边形ABCDEFGH面积的.)

到这里可发现，只要是相似的2个正2n边形，结论都成立，于是推广到一般，即:

2个相似的正2n边形，若较大的正2n边形顶点置于较小的正2n边形的中心，绕其中心旋转，那么重叠部分的面积始终不变，其重叠部分的面积总等于较小正2n边形面积的(其中n≥2).

3 教学启示

3.1 以课本为本，重视数学思想方法的归纳、总结

古希腊哲学家亚里士多德就主张，教师不应直接地把“思想成衣”交给学生，而是需要引导他们自己学会“思想服装”的裁剪.在解题中，我们会遇到很多“相似”问题，尤其是几何图形类问题，一线教师常常会说，这一道与那一道相似，之前也讲过的，于是反问学生:你们怎么又不会了呢?造成学生做不好同类问题的根本原因就是缺少对同类问题的反思、总结.因此，在教学中，要以教材为本，引导学生去思考，帮助学生反思、总结，培养学生良好的反思习惯;教会学生如何去总结，让学生在探索与反思中来真正获得经验，获得思想方法.如第2)小题，如果学生掌握了证明2条线段相等的常用思想方法:直接法与构造法(即证2条线相等，当不能直接证明时，可构造全等形或中垂线)，那么问题迅速得解.

3.2 注重模型化教学，提高解题能力

罗增儒教授在《数学解题学引论》中指出:“学习数学的过程中，所积累的知识经验经过加工，会得出有长久保存或基本重要性的典型结构与重要类型——模式，将其有意识地记忆下来.当遇到一个新问题时，我们辨认它属于哪一类基本模式，联想起一个已解决的问题，以此为索引，在记忆贮存中提取出相应的方法来加以解决.”对于几何图形类问题，这个模式实际上就是基本形，当学生问到图形类问题时，教师高瞻远瞩，一看便知，因为教师的基本形识别意识已经确立了.而学生在解较常见的图形类问题时，为什么不能识别出基本形?笔者认为，最根本原因是学生没有指向性的意识去记忆基本形.最初学生可能想到这个图形在哪里见过，但因没有经过提炼，很难在短时间内回忆起，也许学生在多次反复练习中会悟出其中的基本形，如果这样，学生仍在题海中，那么教师的价值何在?作为一线老师，在平常的教学中，也应注重对典型例、习题的模式化教学，培养学生模式化意识，学会提炼基本形，为我所用.让学生有意识地积累了一些基本模型，逐步养成由一点想一类、悟一片的思维习惯.这样做既能把学生从题海中解放出来，也能提高学生解决问题的能力.

［1］郑毓信.《数学课程标准(2011)》的“另类解读”［J］.数学教育学报，2013(1):1-7.

［2］韩敬.由一道中考试题的多证引发的结论及应用［J］.中国数学教育，2014(4):38-41.