户外漫步机不锈钢曲柄失效分析

文／山西澳瑞特健康产业股份有限公司 沈红斌 郭鹏霞

户外漫步机不锈钢曲柄失效分析

文／山西澳瑞特健康产业股份有限公司 沈红斌 郭鹏霞

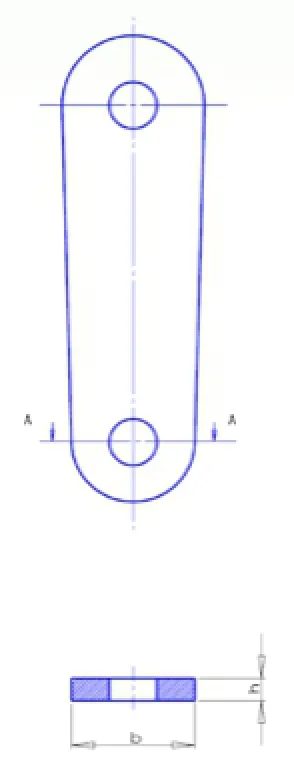
我公司生产的室外椭圆漫步机（如图），由于其锻炼时四肢联动、运动舒适，受到了广大群众的喜爱，在室外锻炼器材中颇受欢迎。2005年，我公司开始生产不锈钢器材供应市场并多次出口欧洲。去年，公司为提高生产效率对曲柄等难加工件采用铸件替代。但器材面市后不久，出现了曲柄疲劳失效现象（如图）。我们就此现象进行了理论分析，分析如下：

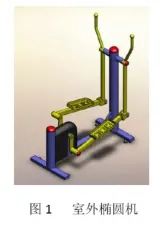
一、户外漫步机两侧为典型的曲柄摇杆机构。

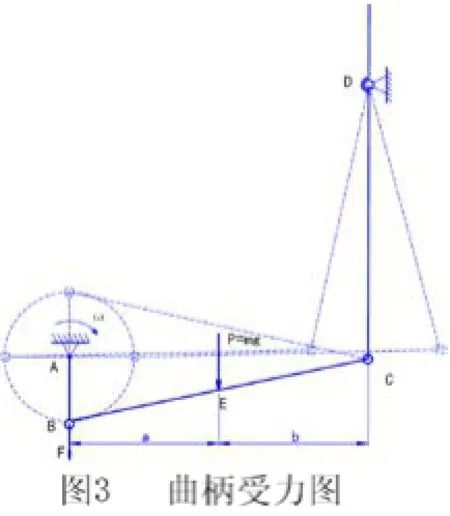
锻炼者站上踏板后，重心完全落在较低踏板一侧。图示为其右侧在最低位置时静止状态下曲柄受力如图3（左端也同）：

Mc＝0 即 F=Pa／b＝mga／b

当a＝b时 F＝mg/2

二、漫步机曲柄运动时动荷系数确定

椭圆机运动时，通过人体重心不断地在两腿之间交替转移变换，驱动曲柄实现旋转运动，进而实现脚部的椭圆运动。

㈠当漫步机以匀速圆周运动时脚部的动荷系数

设曲柄运动50r/min,即ω＝50×2π/60＝1.67π/s；并设定驱动曲柄时，人体重量全部位于驱动腿一侧；由于圆周运动存在的法向加速度，则曲柄踏板轴在最下端受力为

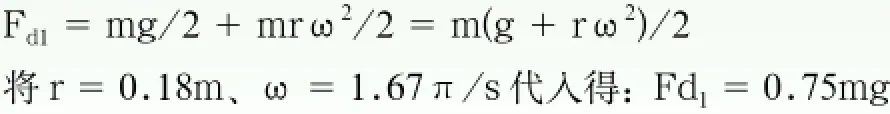
㈡由于户外漫步机结构简单，未设置用于调节运动平稳度的飞轮装置，整机转动惯量很小，因此在其运动过程中曲柄角速度变化较大，有冲击现象。尤其当使用者不熟练或运动起始时，居于上端的曲柄会突然降至低端，此时略去各运动构件的转动惯量及各转点摩擦，曲柄在mg/2力的作用下，运动速度理论上为v=√2gh=√4rg,曲柄踏板轴在最下端受力为：

Fd＝mg/2＋mv2/2r＝（mg＋m×4rg/r）/2＝2.5mg

㈢上述1、2均为特例，难以客观描述实际使用时真实情况。为此笔者专门查阅了相关资料［1］。资料介绍，无飞轮简易椭圆机实际使用中曲柄转速ω变化甚大，其最大角速度ωmax＝4ωmin（甚至更高）。以锻炼者每分钟骑行50周［1］（其平均角速度ωa＝1.67π/s）为例，计算其ωmax、ωmin如下[2]：

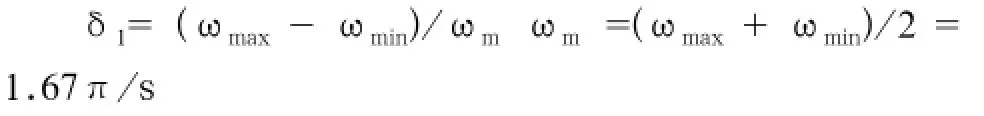
δ 运转不均匀系数

得：δ1=2（ωmax－ωmin)/(ωmax＋ωmin)＝1.2

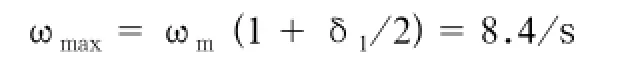
最大角速度位置位于曲柄底部，此时锻炼者对于曲柄踏板轴的作用力为：

Fd3＝mg/2＋mrω2/2＝m(g＋0.18×8.42）/2≈1.15mg

三、运动中曲柄踏板轴、曲柄受力情况分析

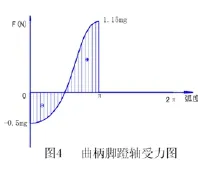
进行受力分析，首先假设其曲柄踏板轴在运动一周中受力状况如图4：在其受力的半周中，其0弧度（曲柄位于最高端）时，锻炼者重心转换后，其受力仅为锻炼者体重－mg/2,(设曲柄踏板轴受力方向为负），π弧度时受力最大为1.15mg。后半周由于锻炼者重心转移到另一侧，该轴不再受力（可以忽略不计）,其受力方程为F=F（θ）cosθ。

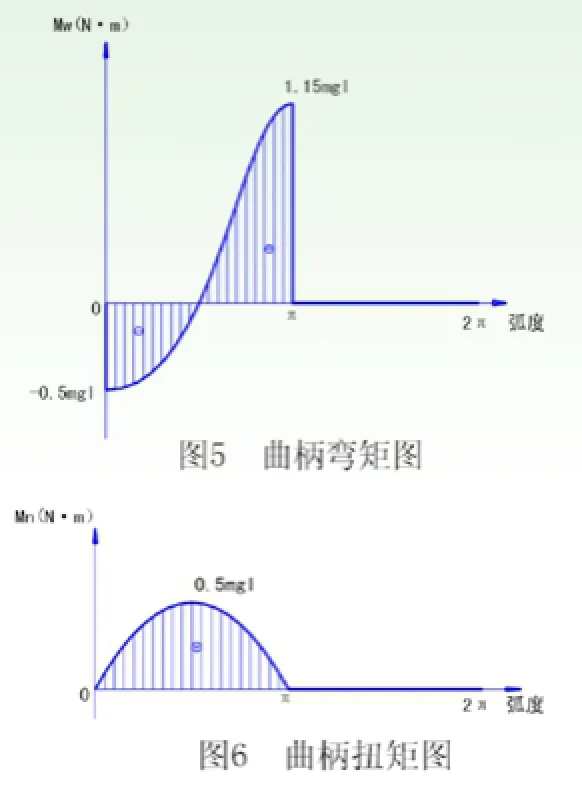
根据以上假设，运动时，曲柄在其受力的半周内，实际受力情况为弯扭组合型。其在一周内承受弯矩、扭矩状况如图5、6。从图中可以看出，在起始位置（0弧度）弯矩为-0.5mgL，扭矩为0；π/2弧度时承受最大扭矩0.5mgL,弯矩为0；π弧度时弯矩最大值为1.15mgL,扭矩为0。曲柄弯矩方程为M=F（θ）rcosθ。曲柄扭矩方程为Mn=F（θ）rsinθ.

与弯矩相比，曲柄承受扭矩值较小，且两者叠加性不强，因此本校核以弯矩为准，扭矩不予计算。

四、疲劳强度校核

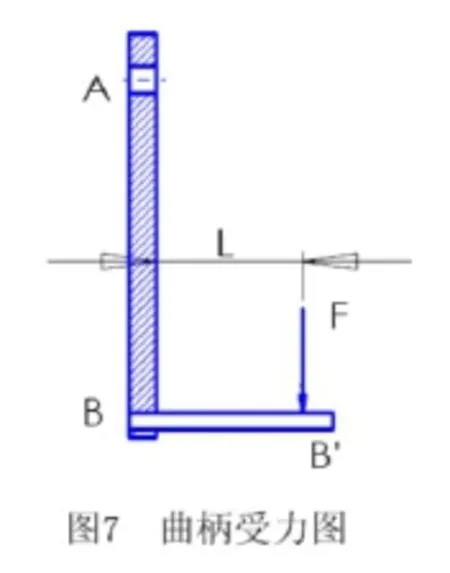
根据国家相关标准要求，椭圆机寿命为八年。在其使用过程中，运动构件长期承受交变载荷，因此必须按照疲劳强度进行校核。漫步机曲柄受力如图7。在曲柄与踏板轴焊接的B-B’处，不仅曲柄抗弯截面模量最小，且该处应力集中严重以及由于焊接缺陷、残余焊接应力等因素均会产生不良影响，因此将其作为曲柄危险截面进行强度校核。

根据上述分析，

曲柄踏板轴轴最大、最小受力分别为

Fmax＝1.15mg Fmin＝-mg/2

曲柄所受弯矩分别为：

Mmax＝FmaxL＝1.15mgL Mmin＝FminL＝-0.5mgL

曲柄截面A所受的正应力分别为

σmax＝Mmax/W＝3Fmaxa/bh2W＝2bh2/6＝bh2/3

σmin＝Mmin/W＝-3Fmina/bh2

将L＝95mm m＝75kg b＝20mm h＝12mm代入得：

σmax＝85.35Mpa

σmin＝-37.1Mpa

应力幅度σa＝(σmax－σmin)/2＝61.2Mpa

平均应力σm＝(σmax＋σmin)/2＝24.1Mpa

工作安全系数nσ＝σ-1/(Kσσa/εσβ＋ψσσm)

曲柄的危险截面位于A-A,此处抗弯曲截面模量最小如图8

㈠当曲柄为304不锈钢铸件时

取304不锈钢铸件的弯曲持久极限

σ-1＝195Mpa［4］

A截面应力集中系数 Kσ＝1.5［3］

尺寸系数εσ＝0.70[3］

表面质量系数 β＝0.65

敏感系数ψσ＝0.05

代入得nσ＝0.96＜1.3[3]

可以看出，安全裕度明显不足。1、上述计算中未考虑焊接应力集中及焊接残余应力的影响，且略去了运动中曲柄受扭矩对其疲劳强度的影响,因此，nσ值相对偏大；2、上述计算中载荷仅限于正常锻炼者，实际使用中，各种不规范使用者比比皆是，其受力状况更为恶劣；3、由于器材制造误差和分体式器材的安装误差，会致使器材曲柄承受额外的附加载荷，进一步降低了安全系数nσ通过上述分析，之所以出现不锈钢曲柄失效就不足为奇了。

㈡当曲柄为304不锈钢机加件时

取304不锈钢的弯曲持久极限σ-1＝205Mpa［4］

A截面应力集中系数Kσ＝1.5［3］

尺寸系数εσ＝0.70[3］

表面质量系数β＝0.95

敏感系数ψσ＝0.05

代入得nσ＝1.47＞1.3

因此，曲柄相对安全

通过上述分析可知，导致两种曲柄工作安全系数差异的原因一是材料本身的弯曲持久极限不等，二是曲柄表面质量系数差异。尤其是承受交变应力的铸钢曲柄，表面粗糙，在承受载荷时，表面应力最高，加上表面的应力集中，容易形成疲劳源，因此，疲劳破坏多从表面开始。找出原因，其应对之策就迎刃而解了。即使采用304不锈钢铸件，只要适当增加危险局面抗弯截面模量，即可满足疲劳强度要求，此处不再赘述。

五、改善漫步机动荷过大的根本措施

根据上述分析可知，曲柄运动的角速度变化过大，在踏板位于底部时形成冲击是造成曲柄疲劳强度不足的主要原因。该冲击力可以使曲柄失效断裂，其对锻炼者的膝关节的冲击可想而知。尤其是中老年人群，长期使用必然会造成膝关节损伤。因此降低运转的不均匀程度，不仅可以降低曲柄部件的冲击力、改善运动的舒畅程度，更可以降低运动时膝关节所受冲击力。而增加飞轮则是最有效的解决方案。根据机械原理[2]可知等效转动惯量计算公式如下：

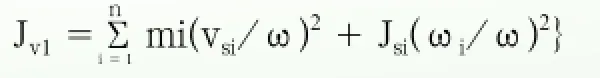
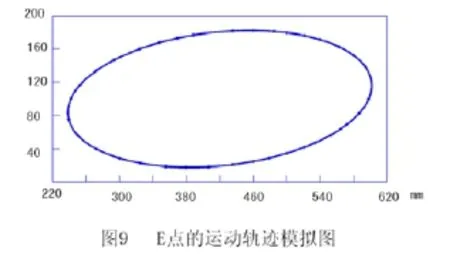
Jv1为器材运动构件匀速运动转化到飞轮轴上的转动惯量，其值可以通过运动参数大致推算出来。锻炼时，锻炼者人体质量交替附着在两脚踏板上并与连杆共同运动，因此人体质量应计入漫步机转动惯量的质量。在漫步机的曲柄摇杆机构中，曲柄、摇杆与人体质量相比小的多，可以忽略不计；两连杆质量计5kg，其质心也位于E处。因此，mi＝人体质量+两连杆质量＝80kg。在锻炼过程中，脚踏板上E点运动速度vsi大小、方向随曲柄转动位置变化而变化。但E点的运动轨迹是一近似以曲柄2r为长轴、r为短轴的椭圆如图9,其周长

L＝2πr/2＋4（r－r/2)＝0.925m

其一个循环内的平均速度Vm＝L/t＝0.925/1.2＝0.77m/s

（t＝60秒/50次＝1.2s）

于是Jv1≈m(vm/ωm)2＝80(0.77/1.67π)2＝1.724kgm2

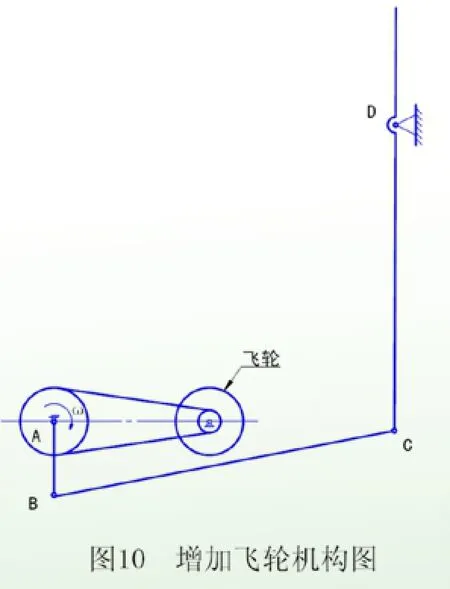
为增加运动舒适性及降低运转不均匀系数，在考虑经济性的前提下，可考虑增加飞轮提高漫步机转动惯量。但由于漫步机本身转速较低，增加飞轮质量低时，效果不明显（如在中轴上增加一φ300mm,重10kg的飞轮，漫步机转动惯量仅增加7%不到，降低总载荷3%），而增加飞轮质量较大时，会增加产品成本。但从Jsi(ωi/ω)2可以看出，增加飞轮的角速度是最有效的方法。如果在中轴上以i＝1/3--1/4,增速传动至飞轮，则漫步机的转动惯量则可得以明显增加如图10。如仍以φ300mm,m1=10kg的飞轮为例，经i=1/4增速传动至飞轮后，漫步机转动惯量增量

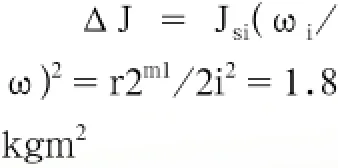
较原漫步机转动惯量增加1倍多，此时漫步机转动惯量

Jv2＝Jv1＋ΔJ＝3.524kgm2

由于增加质量后转动惯量增加，致使运转不均匀系数δ降低，其算式为：

Jv2/Jv1＝δ1/δ2

δ1δ2增加飞轮前、后运转不均匀系数

δ2＝（Jv1／Jv2）δ1＝（1.724／3.524)δ1＝0.49δ1＝0.587

相应的ωmax＝ωm(1＋δ1/2)＝1.284ωm＝6.78/ s

Fd3＝（mg＋mrω2）/2＝m(g＋0.18×6.782）/2＝0.923mg

可见，增加飞轮后，冲击载荷较原来降低35%，总载荷较原来降低20%，仅比匀速转动的Fd1高0.173mg；运转不均匀系数由原来的1.2降至0.587，其运动舒适度会大为提高。以上属于笔者概算，可能与真实状况有所差异，还需进一步验证。

随着全民健身运动的广泛深入开展，户外运动器材运动的可靠性和舒适性并重将成为生产企业努力的方向,而对于户外漫步机的运动舒适性改善工作更具紧迫性。

[1]孙学燕等.体育器材设计.北京:冶金工业出版社,2010.

[2]天津大学.机械原理.人民教育出版社,1979.5.

[3]机械设计编委会.机械设计手册.新版第五卷.机械工业出版社,2006.

[4]成大先主编.机械设计手册.第四版第一卷.化学工业出版社,2006.