压磁式传感器的结构优化与静态标定*

付广洋，于丙强*，赵世霞，赵 健

（1.燕山大学环境与化学工程学院，河北秦皇岛 066004；2.山东大学机械工程学院，济南 250061）

压磁式传感器的结构优化与静态标定*

付广洋1，于丙强1*，赵世霞2，赵 健1

（1.燕山大学环境与化学工程学院，河北秦皇岛 066004；2.山东大学机械工程学院，济南 250061）

为了保证所研制的压磁传感器在安全工作条件下质量最轻，基于ANSYS14.0的优化平台，完成了对压磁传感器体积的优化设计，并进一步研究了各优化参数的敏感性；其次，对传感器的主要静态性能指标进行了标定；然后在不同预载荷，不同测力范围，不同励磁频率条件下对传感器的重复性，线性度和灵敏度进行了实验分析与研究，最后，工业应用验证了该传感器使用周期长，检测信号稳定不失真，检测精度高，为冷轧带钢板形闭环控制奠定了基础。

压磁式传感器；优化设计；静态特性；板形

高精度板形是高级冷轧带钢的重要质量指标，开发高精度的板形测量传感器，寻求合理的检测方法，研制高质量的板形仪对改善板形非常关键和重要［1-2］，压磁式传感器（也称磁弹性传感器）是板形检测单元的重要组成部分，压磁式传感器是利用铁磁材料的磁弹性效应而工作的一种传感器，即利用这种传感器将作用力（如弹性应力，残余应力等）的变化变换成传感器导磁率的变化并输出电信号。它在作用原理，结构以及使用上都与其他类型的测力传感器不同，它具有输出功率大，抗干扰能力强，过载能力强，适宜于在恶劣环境中长期可靠的工作等优点，因此常用于冶金，矿山，运输等工业作为测力与称重［3］。本文对接触式分片内孔压磁式板形仪的检测元件—压磁式传感器进行了优化设计，并对其静态特性进行了标定。

1 压磁传感器的结构优化

1.1 压磁元件

压磁传感器的核心是压磁元件，它实际上是一个力-电转换元件。考虑到实际的工作环境，所研制传感器的冲片为多联冲片，冲片形状如图1所示。

压磁元件常用的材料有冷轧硅钢片，坡莫合金或其他铁氧体材料，最常用的材料是硅钢片。为减少涡流损耗，压磁元件的铁芯大都采用薄片的铁磁材料叠合而成，片与片之间用环氧树脂粘贴，本传感器的压磁元件由52片多联片粘贴而成，如图2所示。

图1 多联冲片

图2 传感器示意图

1.2 压磁元件的优化设计

采用ANSYS有限元分析软件，对压磁元件建立有限元模型并进行加载求解，得出最小体积及设计变量的数值。

1.2.1 建立有限元模型

由于压磁元件是对称体，为简化计算量，取其四分之一建模，如图3所示。

图3 压磁元件的简化模型

整个模型采用 SOLID82单元，SOLID82是ANSYS提供的八节点四边形板单元；采用智能网络划分，利用Smart Size命令进行自由网络单元尺寸控制，智能单元尺寸等级值为3，网络划分情况如图4所示。

1.2.2 约束条件和施加载荷

简化后的连接面上采取对称边界约束，该面上X、Y、Z 3个方向上的位移为零；在压磁元件的上端面，受到50 MPa的压力，压磁元件所承受的最大压力为100 MPa；压磁元件的高度L初始值为12 mm，变化范围为（12±0.03）mm；壁厚t1的初始值为2 mm，变化范围为（2±0.5）mm；圆角半径fil的初始值为1 mm，变化范围为（1±0.25）mm；长度h的初始值为3 mm，变化范围为（3±0.03）mm；厚度d的初始值为0.3 mm，变化范围为（0.3±0.005）mm；优化设计的目的是通过改变压磁元件的t1、fil、L、h、d的尺寸，使得所研制传感器的重量最小。

图4 网络划分情况

1.2.3 求解及后处理

在模型上端面施加50 MPa压力，对模型进行静态分析，绘制Von Mises应力云图，如图5所示。并获得最大等效应力SMAX和总体积VTOT。

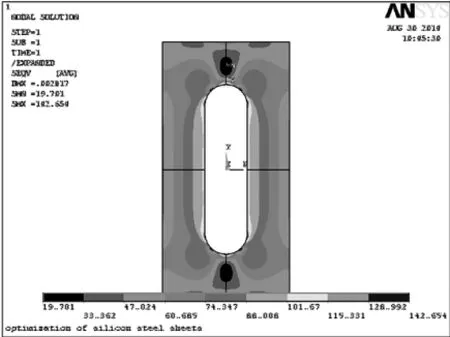
图5 Von Mises屈服应力图

1.2.4 优化处理

计算完成后，保存完整的ANSYS计算流程，生成优化文件［4-6］，将压磁元件的体积作为目标函数，最大Von Mises值作为状态变量。目标函数和状态变量随设计变量的变化规律分别如图6、图7所示。

从图中可以看出，数列13为最优数列。此时，压磁元件的体积最小，而且最大Von Mises应力处在较安全的范围内，此时VTOT=3.337 9 mm3，FIL= 0.755 27 mm，T1=1.540 5 mm；L=12.030 mm；H= 2.977 6 mm；D=0.300 40 mm。

优化设计完成之后的Von Mises应力云图如图8所示。

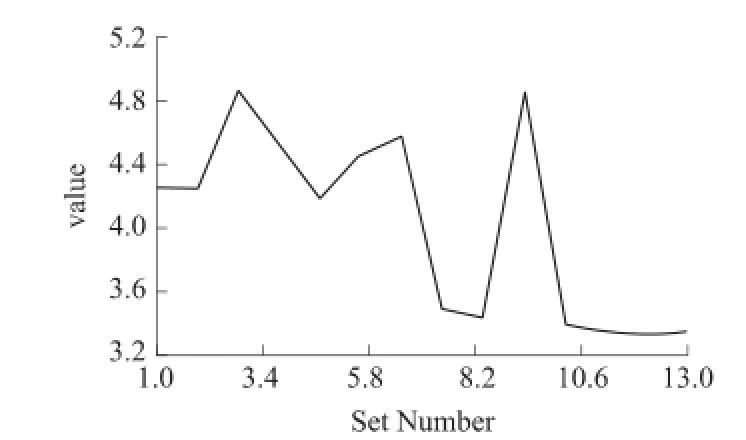
图6 目标函数随设计变量的变化规律

图7 状态变量随设计变量的变化规律

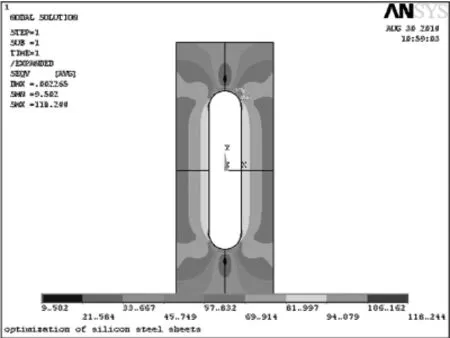
图8 优化后Von Mises屈服应力图

由图8可知，优化之后的压磁元件上受力比较均匀，大约为80 MPa，所承受的最大压力从原来的142.654 MPa变为118.244 MPa；材料的变形量也由原来的0.002 817 mm变为0.002 265 mm。

1.2.5 优化变量的敏感性

为了研究各优化变量对体积以及最大等效应力的影响趋势及敏感性，使用ANSYS优化模块中的梯度优化法在最优结构解附近进行计算，结果如图9、图10所示。由图9可以得知，各优化参数对于体积的影响作用：L＞D＞T1＞FIL＞H；由图10可以得知，各优化参数对于最大等效应力的影响作用：L=D＞H＞FIL＞T1。总结来说，压磁元件的高度L与厚度D对其体积及最大等效应力的影响最大，敏感性最强。

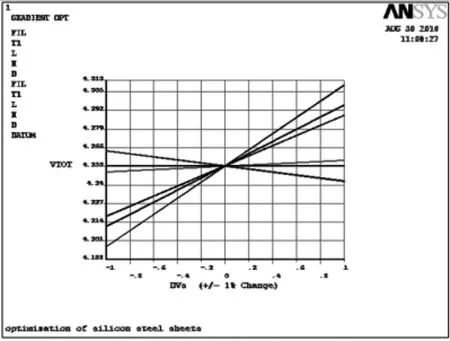
图9 各参数对于体积的影响

图10 各参数对于最大等效应力的影响

2 静态标定实验

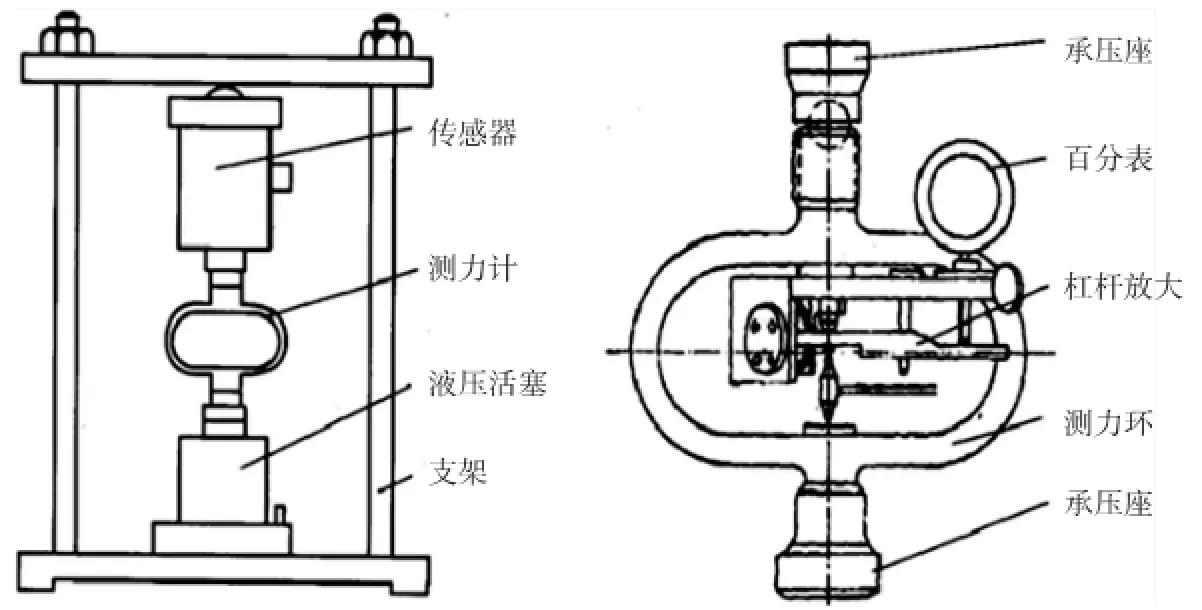
图11 推力标定装置及标准测力计示意图

2.1 传感器静态标定

静态标定的目的是确定传感器静态特性指标，如线性度，灵敏度，滞后和重复性等［7］。

2.2 传感器标定设备

标定对象为所优化的压磁传感器。

实验装置选用环形测力计标定效果较好，标定精度较高，如图11所示。带杠杆放大机构和百分表的环形测力计为标准的推力标定装置，椭圆形钢环受力后的变形量与作用力成线性关系。

2.3 静态标定条件

传感器的静态特性是在静态标准条件下进行标定的。所谓静态标准条件是指没有加速度，振动，冲击（除非这些量本身就是被测量）及环境温度一般为室温（20±5）℃，相对湿度不大于85%，大气压力为（101.3± 8）kPa的情况。另外，此次标定的励磁电源频率为2 kHz，，励磁电压为4.88 V，励磁电流为165.1 mA。

2.4 标定实验数据

实验所测数据如表1所示，标定结果归纳于表2。

表1 连续加卸载实验数据 单位：mV

表2 标定数据结果

3 主要静态性能指标的实验分析与研究

3.1 传感器重复特性指标

传感器的重复性反映传感器的随机误差，是衡量传感器性能的重要指标；选用贝塞尔公式法作为衡量传感器重复性的指标，关于重复性的具体计算方法参考GB/T 18459—2001《传感器主要静态性能指标的计算方法》。

3.1.1 励磁频率为2 kHz时的传感器的重复性实验

①预载改变，最大载荷为6 kN时的连续加卸载试验

预载为0 kN，最大载荷为6 kN的连续加卸载实验数据见表3。其中n=7，采用分段最佳斜率法拟合数据，拟合直线方程为y=65.26x+142.15，满量程输出YFS为391.56。

表3 连续加卸载实验数据

由贝塞尔公式可得传感器的重复性误差ΔR= ±1.46%。可知当预载为0 kN，最大载荷为6 kN时，传感器的重复性很好。

当预载荷为2 kN，最大载荷为6 kN时，此时复性误差为±0.88%；当预载荷为3 kN，最大载荷为6 kN时，此时重复性误差为±0.70%。

可见，当最大载荷6 kN不变时，传感器的重复性随着预载的增大而得到改善（±1.46%→±0.88% →±0.70%），达到最佳预载之后继续增加预载，传感器重复性基本不变。

为了研究最大载荷对传感器重复性的影响，将最大载荷加大到10 kN进行下一组实验。

②预载改变，最大载荷为10 kN时的连续加卸载试验

当预载为2 kN，最大载荷为10 kN时，重复性误差为±1.21%，与预载为2 kN，最大载荷为6 kN时（重复性误差为±0.88%）对比，可以得到结论：当预载不变，最大载荷由6 kN增大到10 kN时，传感器重复性变差（±0.88%～±1.21%）。

预载4 kN，最大载荷为10 kN时，重复性误差为±1.64%；预载为6 kN，最大载荷为10 kN时，重复性误差为±0.96%。

可见，当最大载荷保持10 kN不变时，传感器的重复性随预载增大而得到改善（±1.21%→±1.64% →±0.96%），达到最佳预载后继续增加预载，传感器的重复性基本不变。

综上所述，由于最大载荷为10 kN时传感器的最小重复性误差（±0.96%）大于最大载荷为6 kN时的最小重复性误差（±0.70%），可以初步判定最大载荷的增加使传感器的重复性误差增大。

3.1.2 励磁电压频率为1 kHz时传感器的重复性实验

为了研究频率变化对于传感器特性的影响，按照同样的方法在1 kHz励磁条件下对传感器进行了加卸载实验。结果如下：

当最大载荷为6kN时，保持最大载荷不变，当预载分别为2 kN、3 kN、6 kN时，相应的传感器的重复性误差分别为：±0.71%、±1.02%、±1.07%，此时传感器的重复性随着预载的增加基本不变（±0.71%→±1.02%→±1.07%）。

当最大载荷为10 kN时，保持最大载荷不变，当预载分别为4 kN、5 kN、6 kN、7 kN时，相应的传感器的重复性误差分别为：±0.49%、±0.56%、±0.60%、±1.68%。

实验结果表明：当最大载荷为6 kN时，励磁频率为1 kHz时的传感器的重复性误差（±0.71%）比励磁频率2 kHz时的传感器的重复性误差（±1. 46%）小；当最大载荷为10 kN时，励磁频率为1 kHz时的传感器的重复性误差（±0.49%）比励磁频率2 kHz时的传感器的重复性误差（±0.96%）小；可以初步判定，励磁频率的降低使传感器的重复性误差降低。

3.2 传感器线性度和灵敏度实验指标

传感器的线性度是指传感器的输出与输入之间的线性程度，即输入输出校准曲线与所选定的参考直线之间的偏离程度，是衡量传感器线性特性好坏的指标［8］。随参考直线的性质和引法不同，线性度有多种，本次求解的线性度为最小二乘法线性度；灵敏度描述了传感器对输入量变化的反应能力，是指在静态工作条件下，单位输入所产生的输出。灵敏度是选用传感器首先考虑的关键因素［9］。其具体计算方法参考《传感器主要静态性能指标的计算方法》。

在实际使用中，传感器总是在其重复性最好的情况下使用，因此这里对其重复性较好的5种情况进行线性度和灵敏度的计算：

①工况1：励磁频率为2 kHz，预载力4 kN，最大载荷为10 kN的连续加卸载试验。

②工况2：励磁频率为2 kHz，预载力6 kN，最大载荷为10 kN的连续加卸载试验。

③工况3：励磁频率为1 kHz，预载力4 kN，最大载荷为10 kN的连续加卸载试验。

④工况4：励磁频率为2 kHz，预载力2 kN，最大载荷为6 kN的连续加卸载试验。

⑤工况5：励磁频率为2 kHz，预载力2 kN，最大载荷为10 kN的连续加卸载试验

3.2.1 实验数据分析

表4到表8为5种典型情况的拟合数据，其中yi为传感器输出相对预载输出的增量值，xi为传感器输入相对预载输入的增量；5种典型工况的实验数据求解结果汇总于表9。

表4 励磁频率为2 kHz，预载力4 kN，最大载荷为10 kN的拟合数据

表5 励磁频率为2 kHz，预载力6 kN，最大载荷为10 kN的拟合数据

表6 励磁频率为1 kHz，预载力4 kN，最大载荷为10 kN的拟合数据

表7 励磁频率为2 kHz，预载力2 kN，最大载荷为6 kN的拟合数据

表8 励磁频率为2 kHz，预载力2 kN，最大载荷为10 kN的拟合数据

表9 5种工况下的标定数据汇总

综合考虑表4～表9的实验结果可得到如下结论：①在励磁频率和最大载荷保持不变的前提下，随着预载荷的增大，传感器线性度变好，灵敏度提高；②在初始载荷以及最大载荷保持不变的前提下，励磁频率的降低，传感器线性度变好，灵敏度提高；③在初始载荷以及励磁频率保持不变的前提下，最大载荷的提高，传感器线性度变好，灵敏度提高。

3.2.2 误差的分析

①灵敏度误差分析

选用传感器首先考虑的是灵敏度，如果达不到测量所需的灵敏度，传感器就不能采用，但灵敏度高的传感器不一定是最好的传感器，灵敏度易受传感器本身或外界环境噪声影响，必须用信号与噪声的相互关系全面衡量传感器。

②线性度误差分析

采用环形测力计进行传感器标定实验时，传感器的受力面必须与施加载荷方向保持垂直关系，一旦传感器放置的位置面发生弯曲，沿传感器横截面方向的压力增大或减小，最终会导致传感器线性度变差。

③重复性误差分析

观察连续加卸载试验数据可以知道：传感器重复性变差可能是因为每一个循环实验卸载后，传感器没有完全回到初始位置。将励磁频率为2 kHz，预载为4 kN，最大载荷为10 kN的实验数据表中的正行程的数据与反行程的数据分别与起始数据相减。得到回零后加卸载实验数据，此时重复性误差由原来的±1.64%减小到±0.67%，重复性明显改善。

总之，压磁式传感器虽然优点很多，但是由于铁磁特性还受很多其他因素的影响，因而将使测量结果产生很多误差，主要因素有环境温度，压磁元件的力滞回线，非线性，以及由于电源不稳定使磁化电流变化引起导磁率的初始值的变化，因而压磁效应也发生变化［10-11］；另外压磁元件的制造工艺，包括冲减材料的方向选择，材料热处理时降温速度的控制，冲片粘合时片与片之间的粘合质量，穿线与装配等，都会对传感器的测量结果产生影响。

3.3 工业应用

本次优化设计的压磁传感器已经成功应用于分片内孔压磁式板形仪，该板形仪是一种在线自动检测冷轧带材平直度（板形）的检测装置，适宜于各种冷轧带材平直度的在线检测［12-17］。图12为分片内孔压磁式板形仪检测辊简图，图13为分片内孔压磁式板形仪系统简图。

针对某厂1 050 mm HC六辊可逆冷轧机，此板形仪的灵敏度大于0.1 mV/N，瞬时过载能力100%，耐温大于200℃，完全能够满足现场检测板形的要求，保证最终带钢产品的板形质量。

图12 分片内孔压磁式板形仪系统简图

图13 分片内孔压磁式板形仪检测辊简图

4 结束语

本文对硅钢片式压磁传感器进行了基础的理论与实验研究，首先，对已有的硅钢片式压磁式传感器结构模型进行了优化设计，利用ANSYS14.0软件的优化设计模块，确定了传感器在安全工作条件下最小体积（VTOT=173.570 80 mm3）及相应设计变量的值（FIL=0.755 27 mm；T1=1.540 50 mm；L= 12.030 00 mm；H=2.977 60 mm；D=0.300 40 mm），为硅钢片式压磁传感器的结构设计提供了理论依据，也为设计其他规格和型号的压磁传感器提供了参考；其次，对传感器进行了静态标定实验，实验结果表明所研制的传感器具有极好的灵敏度（S= 76.67 mV/kN），重复性（1.21%），线性度（1.29%）；然后，在不同预载荷，不同的测力范围，不同的励磁频率条件下对传感器进行了重复性，线性度和灵敏度的实验分析与研究，并总结了不同频率下传感器特性变化的规律；最后，结合工业应用证明了此次研制的传感器性能优良，为高精度板形的测量以及带钢板形质量的确定打好了基础。

［1］ 刘宏民，于丙强，杨利坡.整辊镶块智能型冷轧带钢板形仪的研制与工业应用［J］.钢铁，2011，46（12）：87-89.

［2］ 于丙强，杨利坡，刘宏民.冷轧带钢接触式板形仪的研制及其工业应用［J］.仪器仪表学报，2010，31（4）：905-911.

［3］ 单成祥.传感器的理论与设计基础及其应用［M］.北京：国防工业出版社，1999：311-326.

［4］ Zhizhao Che，Fangxin Fang，James Percival.An Ensemble Method for Sensor Optimization Applied to Falling Liquid Films［J］.International Journal of Multiphase Flow，2014：153-161.

［5］ Min-Kyung Kang，Soobum Lee，Jung-Hoon Kim.Shape Optimization of a Mechanically Decoupled Six-Axis Force/Torque Sensor［J］. Sensors and Actuators A：Physical，2014，209（2014）：41-51.

［6］ 吴宝元，申飞，吴仲城.应变式多维力传感器结构优化设计方法研究［J］.传感技术学报，2010，23（10）：1413-1416.

［7］ GB/T 18459—200传感器主要静态性能指标计算方法［S］.

［8］ 彭杰纲，宁静，邓罡.传感器原理及应用［M］.北京：电子工业出版社，2012：4-14.

［9］ 刘清惓，高翔，陈传寅.基于MEMS传感器的水气测量系统［J］.传感技术学报，2014，27（6）：853-856.

［10］张洪润.传感器技术手册（上册）［M］.北京：北京航空航天大学出版社，2010：186-201.

［11］张洪润.传感器技术手册（中册）［M］.北京：北京航空航天大学出版社，2010：815-836.

［12］于丙强.整辊智能型冷轧带钢板形仪研制及工业应用［D］.秦皇岛：燕山大学，2010.

［13］刘宏民，于丙强，华仲新.分片内孔压磁式板形仪：中国，200610048380.1［P］.2007-03-21.

［14］Yang Lipo，Yu Bingqiang，Yu Huaxin.Online Shape Dynamic Wrapping Angle Compensation Model of Cold Strip［J］.Journal of Iron and Steel Research，International，2011，18（7）：28-32.

付广洋（1988-），男，山东潍坊人，燕山大学环境与化学工程学院化工过程机械系硕士研究生，主要研究方向为板形检测与控制，kai0827@163.com；

赵世霞（1990-），女，山东日照人，山东大学机械工程学院机械工程系硕士研究生，主要研究方向为注塑机现代结构优化设计与CAE分析，sdshixia@126.com。

于丙强（1963-），男，山东荣成人，工学博士，研究员，教授级高工，主要研究方向为板形测量系统的研制，ybingq@ ysu.edu.cn；

Structure Optimization Design and Static Calibration for the Magneto Elastic Sensor*

FU Guangyang1，YU Bingqiang1*，ZHAO Shixia2，ZHAO Jian1
（1.College of Environmental and Chemical Engineering，Yanshan University，Qinhuangdao Hebei 066004，China；2.School of Mechanical Engineering，Shandong University，Jinan 250061，China）

In order to get the lightest weight of the magneto elastic sensor which is made by cold-rolled silicon steel sheets under the safety working condition，the structure optimization design of the sensor was completed based on ANSYS 14.0 platform.Moreover，the influence of the design variables on the volume and the Von Mises stress of the sensor is concluded in this paper.Then the static calibration experiment is carried out to figure out the main static performance specification of the sensor.Moreover，some experimental analyses and researches of the designed sensor are carried out under the conditions of different pre-load，different load scope and different magnetism frequency.Finally，application result shows that the sensor has the advantages of stronger anti-interference ability，signal stability，high-precision and long service life.The successful application of the sensor realizes the measurement of strip shape in real-time，and lays a solid foundation for shape control.

cold-rolled silicon steel sheets；magneto elastic sensor；ANSYS 14.0；the structure optimization design；static characteristic；shape

TP391

A

1004-1699（2015）04-0479-08

7230

10.3969/j.issn.1004-1699.2015.04.005

项目来源：国家科技支撑计划项目（2011BAF15B03）；河北省自然科学钢铁联合研究基金项目（E2011203004）

2014-11-16 修改日期：2014-12-25