基于分段线性回归的传感器网络数据压缩传输方法研究*

张瑞瑞，杜尚丰，陈立平，阚 杰，徐 刚

（1.中国农业大学信息与电气工程学院，北京 100083；2.北京农业智能装备技术研究中心，北京 100097；3.国家农业智能装备工程技术研究中心，北京 100097；4.首都师范大学信息工程学院，北京 100048；）

基于分段线性回归的传感器网络数据压缩传输方法研究*

张瑞瑞1，2，3，杜尚丰1，陈立平2，3*，阚 杰4，徐 刚2，3

（1.中国农业大学信息与电气工程学院，北京 100083；2.北京农业智能装备技术研究中心，北京 100097；3.国家农业智能装备工程技术研究中心，北京 100097；4.首都师范大学信息工程学院，北京 100048；）

无线传感器网络通信带宽等十分有限，难以实现较大量数据传输。针对多参数传感器网络，通过提取基准参数数据集，并分段构建线性回归方程的方法，设计了一种适合多参数、较大数据量传感器网络网内数据的压缩传输算法。以某基地实际采样环境温度、空气相对湿度、土壤温度数据为研究对象，对算法压缩效率和数据恢复效果进行了分析。结果表明：对于空气相对湿度和土壤温度，恢复数据与原始数据均方根误差RMSE分别为3.87%、0.49℃时，整体数据压缩率可达51.9%，有效降低了数据传送量。

传感器网络；数据融合；线性回归；相关分析

无线传感器网络WSN（Wireless Sensor Network）是以感知、采集和处理网络覆盖区域中被感知对象的信息为目的，利用大量传感器节点以无线、多跳、自组织方式构成的数据协同处理网络［1-2］。如何有效减少数据传送量，延长网络生命周期，是当前WSN能耗控制研究重点［3-4］。数据压缩传输技术是解决上述问题的有效方法之一［5-6］。

Deligiannakis A等［7］提出了一种基于分段线性回归模型的WSN数据估计算法。算法通过对数据分段处理，从中选出基础信号数据，并传送基于以段为单位的线性回归运算得出的回归方程系数，有效地减低了传感器网络的网内数据传送量。王玲等［8-10］从数据时间相关性分析层面考虑，基于线性回归模型构建了不同的数据压缩算法。杨圣洪等［11］针对数据时间、空间相关性特征，提出了一种基于环模型的分布式时-空小波数据压缩算法。李杨［12］等提出了一种基于小波分段常值压缩的数据收集算法，利用压缩采样理论和分段化方法降低数据传输量。Deepak Ganesa等［13-14］提出了一种基于小波压缩层次系统，基于时空相关性，在节点层对数据时间序列上相关性进行分析，在聚合节点上对不同节点进行空间相关性分析，通过两次处理降低数据冗余。侯鑫、杨永健等［15-17］基于神经网络、卡尔曼滤波等算法模型构建了传感器网络数据融合算法。

考虑到非实时多参数WSN节点环境监测应用背景下，网内参数间表现出强相关、大冗余特点，以及传感器网络节点对数据融合算法的简单、易实现等特殊要求，本文提出了一种基于相关性分析的节点-基站分离式的分段线性回归数据压缩传输算法PWLR（Piece-Wise Linear Regression）。算法通过挖掘参数间相关性，减少网内数据量，延长WSN生命周期。

1 算法的模型描述

传感器节点采集数据可以描述为矩阵结构，如式（1）所示。式中行向量表示单个参数在时间序列上采样数据集。n×m矩阵表示当前最新样本数据，n表示节点有n个监测参数，m表示节点已采样周期数（假设各参数具有相同的采样周期）。

对于强相关性参数（如空气温度和土壤温度），利用标准线性回归估计模型建立参数间数学关系方程，如（2）所示，并基于最小二乘法确定拟合方程拟合误差RMSE最小时的回归系数（a，b）。传感器网络节点将Yj作为基准数据集BD（Base Data）发送至基站，对于Yi数据集的传送则可以通过只发送拟合方程回归系数（a，b）实现。

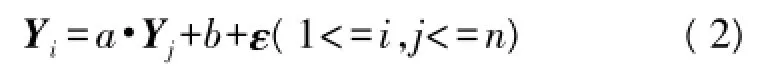
然而，对整个时间序列进行线性回归会产生较大误差，主要原因在于：①参数在不同时间段表现的相关程度不同。例如环境温度在一天的正午时段变化率较小，而傍晚时分变化率较大。②不同参数的相互影响在时间维度上具有滞后性。当某个参数改变时其他相关参数的相应变化会延迟发生。例如环境温度与土壤温度的相互影响。

本文提出一种分段线性回归映射方法，将时间序列上的样本数据划分成段，以段为单位进行线性回归计算，并以自定义结构化精简集S的形式进行特征描述，如定义1。

定义1：结构化精简集S由以下部分组成

·l：段长度；

·start：段在行上的开始坐标，例如该段在行i上的区间可表示为Yi［start，start+l］

·migration：该段做线性回归运算时在基准数据集上的起始偏移量，例如可表示为BD［migration，migration+l］

·a，b，err：a，b为分段线性回归方程的回归系数，err为均方根误差（err用于分段搜索时可不用传输，见2.2节）

当n×m个样本数据采集完毕后，传感器网络节点首先选取基准数据集（设为Yj，见2.1节），并将行i分成「m/l]段（「m/l]表示对m/l的计算值做上取整运算）。每段以长度l搜索Yj上对应的线性回归运算最优数据区间，并将结果以结构化形式发送给基站。基准数据集整体直接发送给基站作为数据恢复依据。每行完成分段回归运算后，该行可用结构化精简集Sk（Sk≪m，k=「m/l]）代替，精简集作为行i的特征描述，用以在基站进行数据恢复。假设Yj是基准数据集，则Yi中的某段数据Yi［start，start+l］可表示为：

a·Yj［migration，migration+l］+b

此时节点数据传输量为：

Data=｛基准数据集，精简集S｝

假设传感器采集参数数据表示与结构化精简集S成员参数的数据表示占用相同存储空间，则数据压缩率可简化表示为：

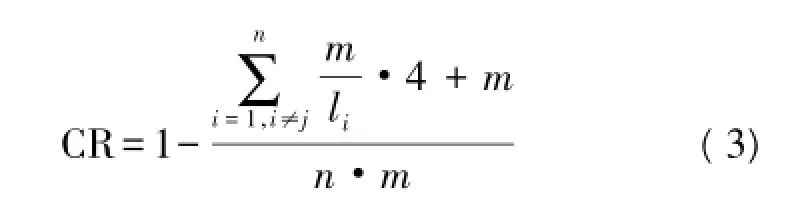
式中：li是第i个参数的分段长度，n是传感器网络节点的监测参数种类数，m是节点已采样周期数。

2 算法实现

算法包括建立和运行维护两个阶段。在能量充足的基站端，算法通过分析历史数据，挖掘单节点多参数间相关性，定义参数相关性贡献评价模型，选取基准数据集，并建立最佳分段方式和动态分段线性映射模型，并将模型参数发送给节点。节点根据基站的配置参数做融合计算，并将基准数据集和精简集S发送基站，基站做恢复运算，得到节点传送数据。基站根据已接收到的数据动态分析并适时更改模型参数，并定时对节点相应配置更新。由于算法复杂的参数选取过程在基站完成，节点只需进行简单的数据映射操作，因此如果忽略基站的能耗，该算法对网络的能量消耗较小。

2.1 算法的建立

2.1.1 基准数据集选取

基站对收集到的感知数据样本进行相关性计算，从中选取一个相关性最高的样本。如式（1）所示，单一节点具有n个感知参数，t时刻第i个参数采集数据表示为yit，时间序列上的传感器数据集描述为矩阵X。为了便于选取，对每行参数建立如下基准数据集评价模型：

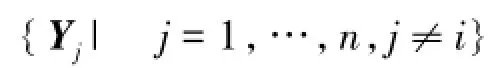
①计算样本相关系数rij。rij表示第i个参数样本与第j个参数样本之间的相关系数，采用简单样本相关系数计算方法，rij定义为样本间协方差与样本各自方差的商，如式（5）：

②计算所有行相关系数和benefit（i），对其进行排序，选择排序最高行作为回归模型基准数据集。

2.1.2 分段线性回归计算。

表1 分段线性回归搜索函数

算法以段为单位进行数据集线性回归映射操作，不同的分段数会给算法带来不同的表现。理论上当分段数较小时，算法误差下降速率较大，随着分段数的增加误差将缓慢下降，当分段数无限增加时，算法误差将趋于0。然而，当段数增加时，每段进行回归估计的数据量减少，这可能导致线性回归的估计误差不减反增，即此时的分段数超过了算法局部最优选择，同时算法压缩率也随之增大。由于压缩率随着分段数的增加线性增长，继续增加分段数反而会降低算法的性能。实际中应该根据需求综合考虑误差和压缩率两方面因素。可以选择算法的局部最优分段，或当误差满足需求阈值时的分段方式。由于不能给出理论上合理的分段方法，将从实验中得出最佳分段方式。

表2 标准线性回归函数

2.2 算法执行与维护流程

基站以一定的周期动态更新基准数据集，提高数据估计精度。同样，基站将以一定周期进行最佳分段的更新操作，提高数据估计精度。算法执行与维护流程如图1所示。

图1 算法执行与维护流程图

3 实验分析

以北京市小汤山国家精准农业示范基地2013 年5月2日～5月11日实际采样数据为实验样本，其中包含环境温度、空气湿度、土壤温度3个参数，参数采样周期为10 min，其中5月2日～5月6日共5天数据进行基站算法初始化参数计算，5月7日～5月11日数据进行节点实验，为了及时感知监测参数变化，基站的算法参数更新周期设为5天。算法数据恢复精度以式（6）所示均方根误差（RMSE）作为衡量标准，并与ISDT算法进行对比［9］。根据三参数的贡献值如表3所示。选取环境温度为基准数据集。

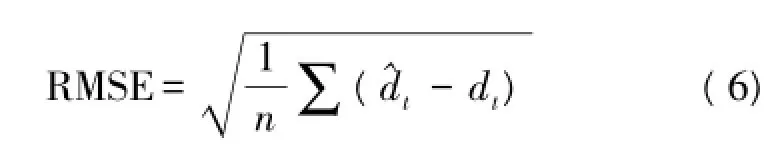
表3 仿真参数贡献值

为了进行样本最优分段，实验以不同段数为变量，以算法RMSE误差为输出，分别对空气湿度，土壤温度进行算法仿真，实验设置分段范围为1～30，结果如图2所示。可以看出，当节点对两种数据不进行分段，直接以数据样本整体进行线性回归计算时，虽然此时数据压缩率最好为33.78%（每行参数只需用一个精简集描述），但其误差达到最大值，分别达到1.8和12.2%。当对数据进行分段线性回归后，开始时算法RMSE降低速率较快，当增加某个值时（实验中土壤温度为16，空气相对湿度为18），算法误差达到局部最优值，此时的分段数使得数据相关性达到局部最佳。当分段数继续增加时，误差开始增加，这是由于样本数据总数不变，随着分段数的增加，每段进行回归估计计算的数据减少。此后算法RMSE变化趋于平缓，继续增加分段数将不会带来算法表现的明显提升，反而导致压缩率的增加。本文采用局部最优解的方式选取分段数。

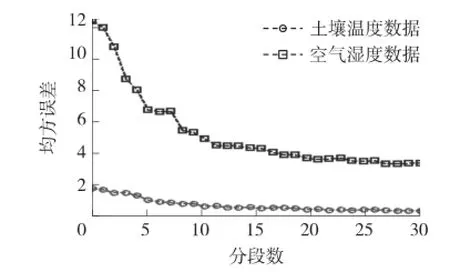
图2 不同分段下算法均方根误差

通过分析均方根误差和压缩率变化关系进行算法比较，结果如图3和图4所示。图3可以看出，当压缩率较小时，压缩的数据足够描述参数的变化特征，基于时间序列分段线性化的ISDT算法能够获得较小的压缩误差，随着压缩误差增加，压缩率超过70%时，ISDT算法压缩误差超过PWLR算法，此时压缩数据量较少，PWLR算法能够更加准确的还原数据。图4所示的空气湿度数据具有类似的特点，当数据压缩率超过60%时，PWLR算法压缩误差明显小于ISDT算法。从中可以看出，PWLR算法能够在高压缩率的需求下获得更加准确的压缩效果。相比于ISDT，PWLR算法更加适合于大数据、高压缩比、高精度的应用需求下。

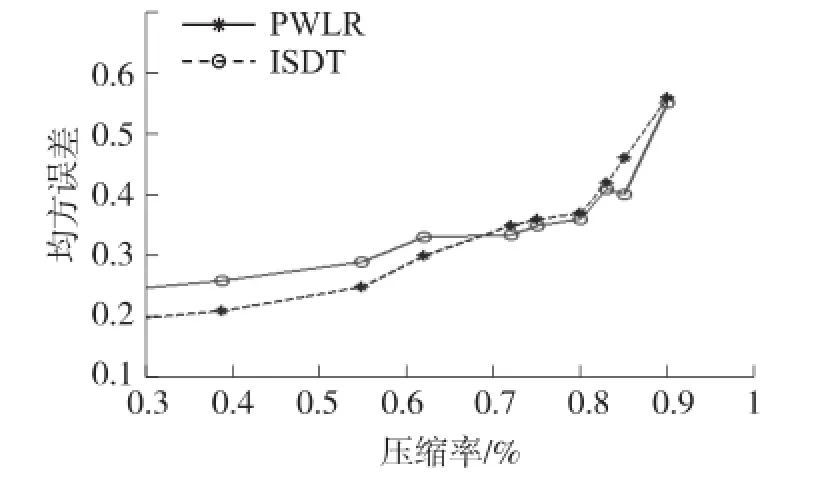
图3 土壤温度数据均方误差与压缩率关系

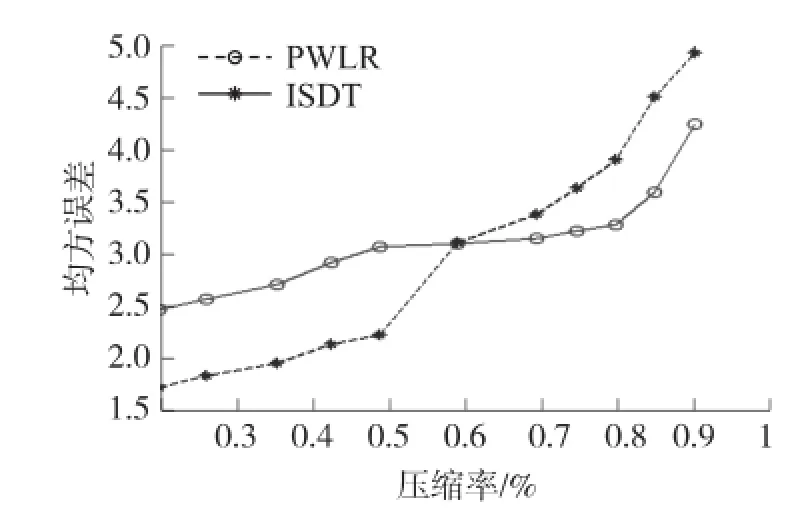
图4 空气湿度数据均方误差与压缩率关系

当土壤温度数据集分为16段，空气相对温度分为18段，进行回归运算时，基站根据精简集对数据恢复效果如图5和图6所示。

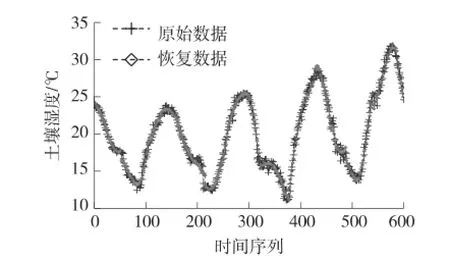
图5 土壤温度恢复数据与原始数据对比

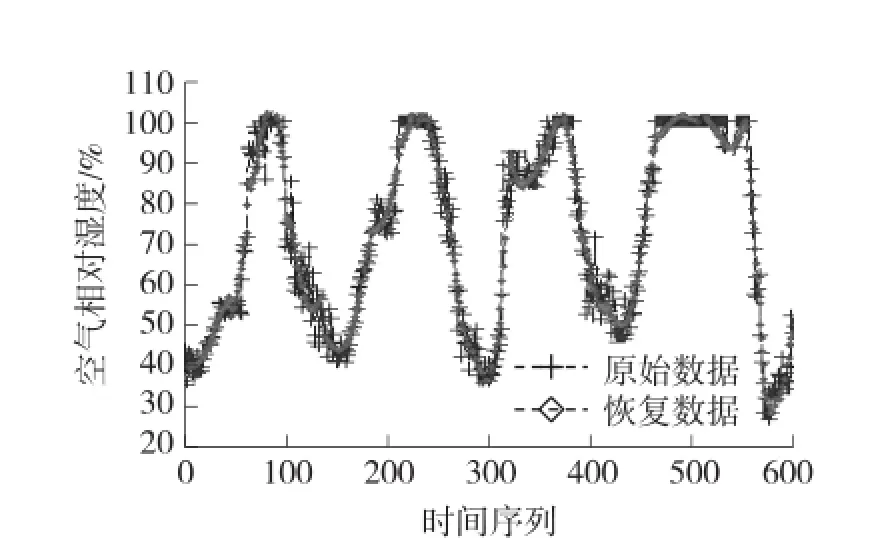
图6 空气相对湿度恢复数据与原始数据对比

可以看出算法能够根据基准数据集准确给出融合数据的特征描述。对于土壤温度和空气相对湿度，恢复数据与原始数据均方根误差RMSE分别为0.49℃、3.87%，此时整体数据压缩率可达59.1%。

4 结论

分布密集的众多节点使得传感器网络内部产生了巨大的数据传输量。如何对数据进行有效压缩以应对WSN资源受限的现状是WSN应用研究中一项具有挑战性的课题。针对监测参数间相关性特点，本文给出了一种基于分段线性回归的多参数WSN数据融合算法PWLR。仿真实验表明，算法以基准数据集为自变量，对分段数据进行最优线性回归搜索，最小化回归方程误差，从而在高压缩率的条件下保证数据融合质量，较原始传输策略显著降低数据传输量。

［1］ Akyildiz I F，Su W，Sankarasubramaniam Y，et al.A Survey on Sensor Networks［J］.IEEE Communication Magazine，2002，40 （8）：102-114.

［2］ Yick J，Mukherjee B，Ghosal D.Wireless Sensor Network Survey ［J］.Computer Networks，2008，52（12）：2292-2330.

［3］ 林蔚，韩丽红.无线传感器网络的数据压缩算法综述［J］.小型微型计算机系统，2012，33（9）：2043-2048.

［4］ 陈正宇，杨庚，陈蕾，等.无线传感器网络数据融合技术研究综述［J］.计算机应用研究，2011，28（5）：1601-1604.

［5］ 康健，左宪章，唐力伟，等.无线传感器网络数据融合技术［J］.计算机科学，2010，37（4）：31-35.

［6］ Nakamura E F，Loureiro A A F，Frery A C.Information Fusion for Wireless Sensor Networks：Methods，Models，and Classifications ［C］//ACM Comput.2007，39：9.

［7］ DeligiannakisA，KotidisY，RoussopoulosN.Compressing Historical Information in Sensor Networks.In Proceedings of ACM SIGMOD Conference，2004.

［8］ 王玲，石为人，石欣，等.基于时间相关性的无线传感器网络数据压缩与优化算法［J］.计算机应用，2013，33（12）：3453-3456.

［9］ 王举，房鼎益，陈晓红，等.文物监测中无线传感器网络数据压缩算法［J］.西安电子科技大学学报，2012，39（1）：157-162.

［10］宋欣，王翠荣.基于线性回归的无线传感器网络分布式数据采集优化策略［J］.计算机学报，2012，35（3）：568-580.

［11］杨圣洪，贾焰，周四望.无线传感器网络基于虚拟节点的小波压缩算法［J］.软件学报，2013，24（3）：557-563.

［12］李杨，郭龙江，李金宝，等.传感器网络基于小波分段常值压缩的数据收集研究［J］.仪器仪表学报，2013，34（1）：119-127.

［13］Deepak Ganesan，Deborah Estrin，John Heidemann.DIMENSIONS：Why do We Need a New Data Handling Architecture for Sensor Networks？［C］//Proceedings of the ACM HotNets，ACM，2002：143-148.

［14］Ganesan D，Greenstein B，Perelyubskiy D，et al.An Evaluation of Multi-Resolution Search and Storage in Resource-Constrained Sensor Networks［C］//Proceedings of the First ACM Conference on Embedded Networked Sensor Systems（SenSys），2003.

［15］侯鑫，张文东，钟鸣.基于事件驱动和神经网络的无线传感器网络数据融合算法研究［J］.传感技术学报，2014，27（1）：142-148.

［16］杨永健，刘帅.基于SOFM神经网络的无线传感器网络数据融合算法［J］.传感技术学报，2013，26（12）：1757-1763.

［17］Olfati-Saber R.Distributed Kalman Fltering for Sensor Networks ［C］//Proc 46th IEEE Conf Decision and Control，New Orleans，LA，2007.

张瑞瑞（1983-），男，博士生，国家农业智能装备工程技术研究中心助理研究员，主要从事传感器网络、传感器智能化技术研究，Rui7986@126.com；

陈立平（1973-），女，国家农业智能装备工程技术研究中心研究员、博士生导师，主要从事农业智能装备技术与系统研究，Chenliping@iea.ac.cn。

杜尚丰（1961-），男，中国农业大学信电学院教授、博士生导师，主要从事复杂系统建模与控制，无线传感器网络理论，机器人控制技术研究，Ca800@ 263.net；

Data Compression Method with Piece-Wise Linear Regression in WSN*

ZHANG Ruirui1，2，3，DU Shangfeng1，CHEN Liping2，3*，KAN Jie4，XU Gang2，3
（1.College of Information and Electrical Engineering，China Agriculture University，Beijing 100083，China；2.Beijing Research Center of Intelligent Equipment for Agriculture，Beijing Academy of Agriculture and Forestry Sciences，Beijing 100097，China；3.National Engineering Research Center of Intelligent Equipment for Agriculture，Beijing 100097，China；4.College of Information Engineering，Capital Normal University，Beijing 100048，China）

Suffering from the limitation of bandwidth，WSN is confronting the challenge of big data transmission.By obtaining Base-data and constructing piece-wise linear regression equation，this paper proposed a data compression transmission algorithm for WSN with large data volume and strong correlation and redundancy multi-parameter.Taking environment temperature，relative air humidity and soil temperature data obtained by a WSN system located in Beijing Xiao Tangshan national demonstration base of precision agriculture as research object，we tested the compression and data recovery efficiency of the algorithm.Results show that data compression ratio is as high as 51.9% when the RMSE between restored data and raw data are 3.87%and 0.49℃，which brings an enormous reduction of the amount of data transmission.

WSN；data fusion；linear regression；correlation analysis EEACC：7230

TP391.9

A

1004-1699（2015）04-0531-06

10.3969/j.issn.1004-1699.2015.04.014

项目来源：北京市自然科学基金项目（4121001）；北京市农林科学院青年科研基金项目（QNJJ201217）；国家863高技术研究发展计划项目（2012AA101901）

2014.11.6 修改日期：2014.12.24