基于容积卡尔曼平滑滤波的管道缺陷定位技术*

杨理践，李 晖，周福宁，靳 鹏

（沈阳工业大学信息科学与工程学院，沈阳 110870）

基于容积卡尔曼平滑滤波的管道缺陷定位技术*

杨理践，李 晖*，周福宁，靳 鹏

（沈阳工业大学信息科学与工程学院，沈阳 110870）

针对管道测量系统MEMS惯性元件的漂移，且难于获得GPS信息进行有效误差累积抑制的问题，创建了管道测量系统9维系统状态误差方程和基于速度差和基准点位置差的观测方程，提出采用容积卡尔曼平滑滤波算法。该算法由以里程轮速度为观测量的正向容积卡尔曼滤波算法和以基准点位置为起点的反向平滑两级滤波组成，实现管道缺陷地理坐标的最优估计。管道缺陷定位实验结果表明，该算法能有效补偿长航时导航参数误差，10 km测量精度可以达到10-3数量级，能够满足管道内检测定位精度要求。

组合导航；管道定位；容积卡尔曼滤波；平滑滤波；定位误差校正

管道运输具有安全可靠、成本低、效率高的特点，已成为石油和天然气运输主要手段。为保证管道的运输安全，需要定期对管道进行检测。目前通用的检测方法是利用管道内检测器PIG（Pipeline Inspect Gargy）在管道内运输介质的推动下，沿管壁向前爬行，PIG携带的检测传感器和记录装置获取经过处的管壁状态的数据，通过对所记录数据进行离线处理，实现对管道腐蚀、壁厚、裂纹等缺陷的检测和评估并确定检测缺陷的位置。如果仅仅根据里程轮和地面人工跟踪记录PIG行走的距离以及自身的周向坐标［1］，难以进行缺陷的精确地理定位，导致开挖维护成本增加。因此，在PIG上安装捷联惯性导航系统 SINS（Strapdown Inertial Navigation System），在检测缺陷的同时实现缺陷的定位、管道地理坐标测量、管道位移的测量［2-3］。

PIG中SINS的惯性传感器是三轴MEMS的加速度计和三轴MEMS陀螺仪，当对所采集的数据通过解算可得到PIG的位置、速度和姿态信息，其误差源于传感器误差、传感器敏感轴垂直误差、各种坐标变换、非线性系统误差及计算误差。由于MEMS器件误差、模型误差和算法误差的存在，使得基于MEMS-SINS的管道测量系统运行10 min～20 min时的定位误差达到数10 km。要计算出精确的管道即时位置，必须推断每次计算的误差累积数值，及时修正以消除下一时刻导航计算的累积误差。误差估计通常采用里程轮、GPS等辅助导航设备与SINS构成组合导航系统，利用EKF、UKF滤波算法实现对导航位置、速度、姿态和传感器误差的估计［4-5］。王延东、贾宏光等采用 Bierman-Thorton算法，避免了EKF滤波算法中雅克比矩阵的计算和滤波增益计算中产生的截断误差随迭代次数增加而累积，获得较高的导航精度和数值稳定性［6］。2009年Simon Haykin等提出的容积卡尔曼滤波 CKF（Cubature Kalman Filter）［7］，该方法采用一组容积点集计算非线性变换后的随机变量均值和方差，该算法避免了线性化误差和雅克比矩阵的计算，具有更优的非线性逼近性能、更高的数值精度和滤波稳定性、实现简单等特点［8］。杨理践等充分利用里程轮和重锤的误差不累积的特点，采用UKF算法融合了里程轮对检测器速度校准和重锤对检测器姿态角校准以提高定位的精度［9］；然而受重锤器件安装误差和测量精度的影响，该方法对于较大的姿态误差角有较好的校正效果，对于小姿态角误差引起的定位误差修正效果不明显。另外，里程轮因机械故障、打滑、轮半径磨损和管壁残留物沉积等因素导致仅以里程轮速度为辅助导航存在某些不确定性，长航时定位误差仍然有较大的可能，甚至发散［10］。

针对海底管道不易获得GPS信息，且管道内用于修正导航发散信息很少的问题。本文根据PIG运行的特点，采用正向以PIG导航速度自约束为观测量的CKF滤波算法和以管道末端基准点位置信息为观测量的反向平滑算法相结合的CKF平滑滤波算法，实现基于惯导长航时的管道定位误差修正。模拟管道运行实验结果表明，所提出的算法能够有效地修正定位误差。

1 导航滤波原理与数学模型

惯性导航系统是通过含有陀螺仪测定的角速度的姿态积分方程，通过四元数解算得到姿态变换矩阵，将加速度计测量的载体加速度数据转换到选定的导航坐标系中；在导航系下，对加速度进行一次积分，得到载体导航速度，对速度二次积分得到载体的位置信息。因此导航算法中姿态、速度、位置3个积分方程的计算误差应低于IMU传感器误差，达到可忽略的程度才能有效保证导航精度的要求。然而惯性敏感元件测量过程中存在环境噪声和器件噪声等测量噪声，导致姿态、速度和位置计算误差随时间的增长迅速累积，使导航精度下降［11］。提高导航精度的有效解决方法是通过外部辅助传感器信息进行抑制［12］。

1.1 速度约束观测模型

由于PIG运行于管道内部，PIG与管壁无缝接触，PIG在管内只产生旋转和沿管线运动，不产生横向和垂向位移，因此在导航定位计算中，垂直于管线方向的速度几乎为0。根据导航微分方程

将式（3）、式（4）代入式（5）得

b系导航计算速度与传统里程仪间接测量速度之差作为PIG沿管道方向的观测量。里程仪是传统的测距仪表，其输出的信息为单向位移信息，除以采样周期与转动计数的积，为载体的即时速度。因此由式（6）得到的观测方程记为：

v观测误差项为：

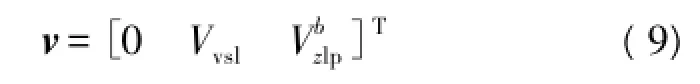
1.2 导航误差状态模型

导航地理坐标系选为东（E）、北（N）、天（U）坐标系。由于各种误差源影响，真实导航地理坐标系（n系）与导航计算地理坐标系（系）之间存在偏差，导致导航计算误差。用欧拉角δφ=（φe，φn，φu）T表示导航系和计算系c之间的失准角，其中φe、φn和φu分

n系、c系和 b系之间的姿态误差矩阵关系式为：

对式（12）两边求微分，将式（11）、式（13）、式（14）分别代入得：

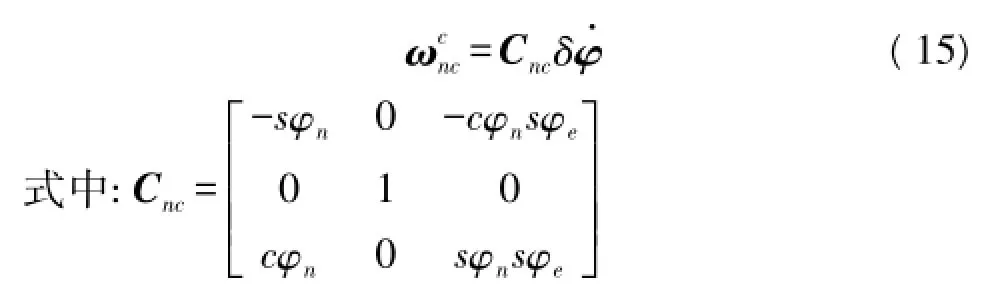
姿态动态误差传递方程为：

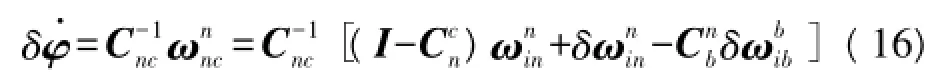
由式（16）可以看出姿态误差方程为非线性的。速度误差动态传递模型为：

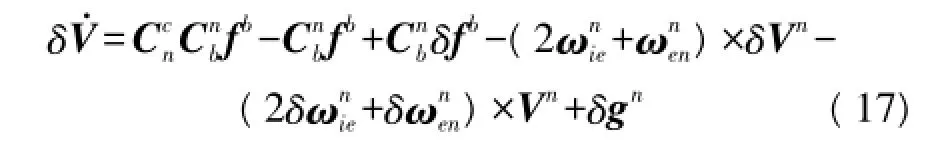
位置误差方程：

2 CKF及基准点平滑算法

管道内检测定位中，由于捷联惯导中器件误差、解算误差引起的定位参数迅速发散，要计算出精确的管道即时位置信息，必须推断每次计算的误差累积数值，及时修正以消除下一时刻导航计算的累积误差。误差估计通常采用组合导航非线性滤波算法。处理非线性的滤波算法最早采用扩展卡尔曼滤波（EKF）算法，利用泰勒展开式的一阶项近似非线性表达式，对于强非线性会产生线性化误差，导致滤波器性能降低。无迹卡尔曼滤波算法（UKF）是利用一组近似高斯分布的采样点，通过Unscented变换来进行状态与误差协方差的递推和更新，避免了对非线性方程的线性化过程且无需计算雅克比矩阵［13］。容积卡尔曼滤波 CKF（Cubature Kalman Filter）采用一组容积点集计算非线性变换后的随机变量均值和方差，该算法避免了线性化误差和雅克比矩阵的计算，具有更优的非线性逼近性能、更高的数值精度和滤波稳定性、实现简单等特点［14-15］。

2.1 基于速度差的CKF算法

设非线性系统：

式中：x（t）为系统误差状态向量，z（ti）为系统里程仪速度观测向量。w（t）和v（ti）分别是互不相关的、零均值白噪声型的系统过程噪声和观测噪声。并且设E｛w（t）wT（t+τ）｝=Q（t）δ（τ），Q（t）为系统噪声方差，E｛v（ti）vT（tj）｝=R（ti）δij，R（ti）为观测噪声方差。采用离散CKF算法，避免矩阵积分，易于递推实现。经离散化处理后得到非线性系统离散化状态方程和观测方程。

针对离散非线性系统的Cubature卡尔曼滤波算法分为3个步骤：第1步是计算容积点和权值，第2步是时间更新，第3步是测量更新。具体算法如下：

①计算容积点和权值

利用Spherical-Radial准则选取2n个计算加权函数为标准正态分布密度的容积点。

②时间更新

2.2 基于基准点平滑滤波算法

通常管道沿线没有GPS位置信息，无法实现常规基于观测GPS位置参数的导航误差状态估计，但管道出口处的位置信息是已知的，因此可通过平滑滤波思想充分利用管道出口基准点的位置信息对导航参数的误差进行平滑滤波，实现位置测量误差的进一步校正。

式中：上标-、+分别表示状态和方差预测和更新。由于导航系统状态维数较多，算法可将导航误差方程中非线性部分采用CKF，线性部分采用传统常规KF滤波方式。这样处理既保证了非线性部分的滤波效果又大大减少了CKF过多容积点计算量。

在此滤波中，状态x（t）=［δγ，δθ，δφ，δVe，δVn，δVu，δλ，δl，δh］T为9维误差向量，其中δγ，δθ，δφ分别为横滚角、俯仰角和航向角误差，δVe，δVn，δVu为东北天（ENU）方向速度误差，δλ，δl，δh为纬度、经度、高度误差。

根据摄动原理，设xs，k为平滑滤波后管道惯性测量系统输出向量，并有

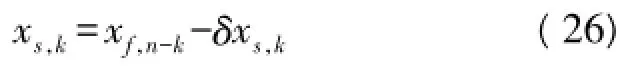
式中：δxs，k为xf，n-k的摄动向量，是构成平滑滤波向量的一部分，k为平滑滤波时刻tk。

设xs，0是导航计算时间序列终点的位置状态向量，其协方差为Ps，0，并且当检测系统处于静止稳态时Ps，0=∞。构造新状态向量为：

对式（27）求微分，得到时间更新等式

上述管道惯性位置测量导航误差估计经过基于速度约束的CKF滤波，消除部分误差，经式（25）补偿后的位置作为后级平滑滤波的参考轨迹，再通过式（26）、式（29）利用管道末端基准点位置信息向起始点逐点进行平滑滤波，进一步提高管道惯性测量系统测量精度

3 实验与分析

为了验证管道定位中导航速度自约束CKF误差估计与管道末端基准点平滑滤波方法的有效性。进行了多次模拟管道环境的装载管道测量系统的小车拖拉实验，运行轨迹包括曲线、直线、Z字型等。本文选用直线、曲线都涵盖的组合实验，数据源自PIG上的MEMS惯性测量单元（NV-IMU300），IMU器件参数如表1。

实验过程为管道测量系统启动后静置时间5 min完成预热、静态对准。小车启动初始段为直线运动，用于动态初始对准，小车绕运动场匀速行驶一圈，第二圈弯道处进行人为制造大的振荡，加减速等异常状况，而后继续平稳运行，停止后静置15 min保存数据，总行程为850 m。IMU采样频率为312 Hz，里程轮采样频率为100 Hz。

表1 惯性器件（IMU）主要参量表

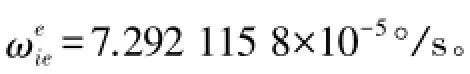
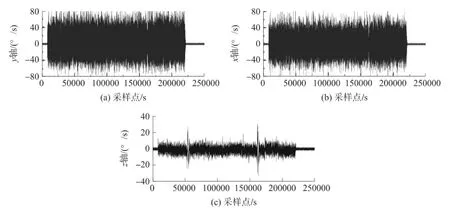
图1 IMU三轴陀螺仪测量值

图2 IMU三轴加速度计测量值

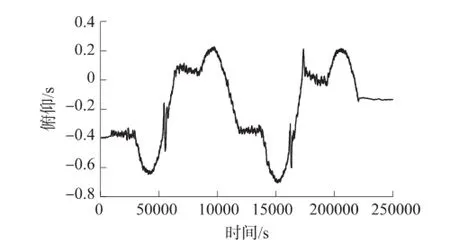
图3 管道测量系统俯仰角姿态解算值

图4 管道测量系统横滚角姿态解算值

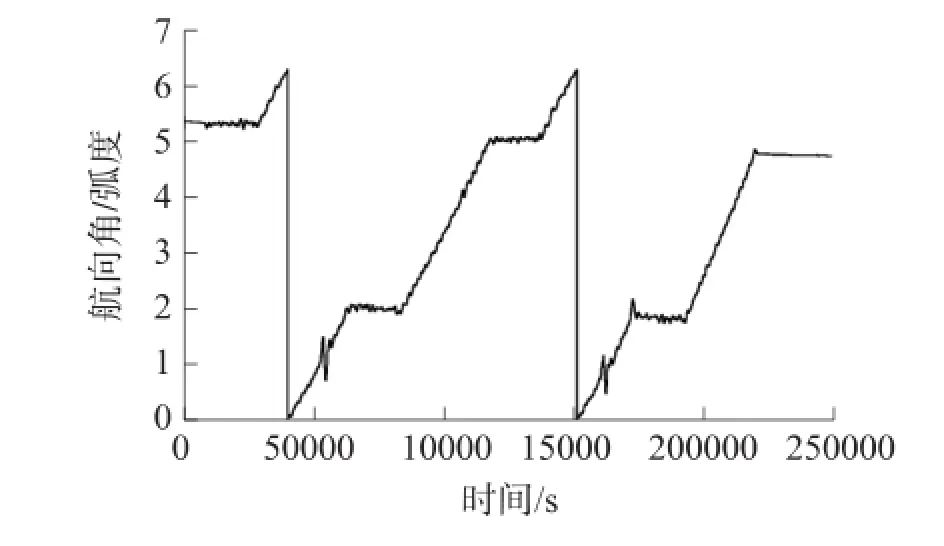
图5 管道测量系统航向角姿态解算值

图3～图5为姿态角滤波曲线，CKF滤波和CKF平滑滤波对于横滚角、俯仰角形状基本一致，均差在0.023°。而滤波后的航向角在第二圈第二个弯道后有明显的航向偏移，这主要是地面不平或人为拉动导致试验车产生滚转振动和颠簸引起横滚角和俯仰角异常变化，致使产生耦合航向角误差。里程仪速度因打滑、停转也是产生滤波精度不高的一个主要原因。在实验中，适当处理里程轮打滑和停转现象，再通过终止基准点平滑算法对前一次滤波做进一步校正。测量轨迹如图6所示。

图6为同一组实验数据的3种滤波方式的轨迹对比图，从图6可以看出，仅EKF滤波算法得到的测量轨迹距离初始位置不远就有较大偏差，且很快偏离标准轨迹，而单纯CKF正向滤波算法使得PIG在运行距离500 m之内的测量精度尚可接受，在第二圈转弯后的偏离较大。经本算法滤波处理得到的运行轨迹测量曲线，在无颠簸平稳运动的约束条件不能满足的情况下，轨迹测量准确性优于EKF和CKF。定点对比测量误差见表2，纬度最大为0.000 001 2°，经度最大为0.000 006°。按此计算假设误差线性增长，则10 km长输管道测量纬度误差为0.001 4°，经度误差约为0.007°，可以满足长距离管道测量精度要求。

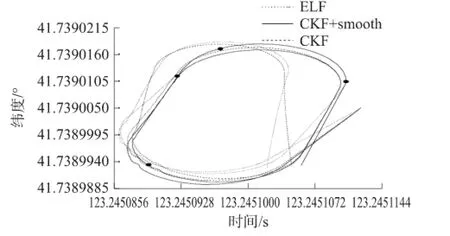
图6 运行轨迹测量曲线图

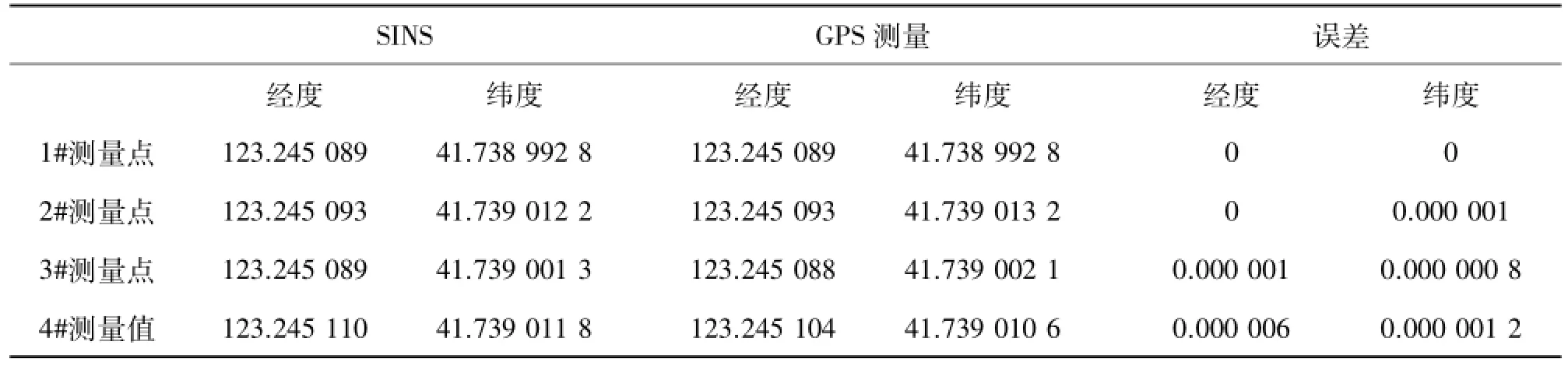
表2 试验轨迹地理坐标测量误差

4 结论

针对油气管道内可用修正导航数据信息缺乏问题，根据管道内检测器结构及其在管内运行特征，利用正向基于里程轮速度自约束与反向基准点位置平滑两级组合滤波算法实现管道位置的最优估计。因基准点位置信息在终点处可获得，由起点至终点的运行过程中，导航误差由前级CKF滤波校正，其输出为后级平滑的参考量。后级滤波以管道末端基准点位置信息为观测量，对前级滤波输出进行平滑滤波，一定程度上修正了前级导航速度自约束，无颠簸平稳运动的约束条件不能满足所产生的误差，实现导航误差的估计及导航参数的校正。这种方法的优点是：CKF滤波算法避免了EKF算法的雅可比计算和线性化误差；无颠簸平稳运动的约束条件不能满足情况下，充分利用管道出口基准点信息实现导航误差的估计及导航参数的校正。实验证明该算法10km管道测量精度可以达到10-3，能够满足长距离油气管道的在线检测与定位。

［1］ Panev A A，Vavilova N B.The Navigation Problem for a Pipeline Inspection System［J］.Moscow University Mechanics Bulletin，2011，66（1）：13-15.

［2］ 杨理践，李振，高松巍.管道检测中管道定位系统研究［J］.无损探伤，2007，6（3）：27-29.

［3］ 杨理践，杨洋，高松巍，等.管道地理坐标内检测的里程校正算法［J］.仪器仪表学报，2013，34（1）：26-31.

［4］ 白亮，严恭敏，朱启举，等.里程计辅助的捷联惯导系统研究［J］.弹箭与制导学报，2013，33（6）：16-18.

［5］ 刘鹰，胡彦亮.基于数字里程仪的INS/里程仪导航系统［J］.弹箭与制导学报，2008，28（4）：59-62.

［6］ 王延东，贾宏光.组合导航系统滤波器截断误差抑制方法［J］.传感技术学报，2014，27（5）：616-621.

［7］ Arasaratnam I，Haykin S.Cubature Kalman Filter［J］.IEEE Transactions on Automatic Control，2009，54（6）：1254-1269.

［8］ 孙枫，唐李军.Cubature卡尔曼滤波与Unscented卡尔曼滤波估计精度比较［J］.控制与决策，2013，28（3）：303-309.

［9］ 杨洋，杨理践，沈博.管道地理坐标测量误差校正方法的研究［J］.传感技术学报，2012，25（10）：1416-1421.

［10］翁浚，成研，秦永元，等.车辆运动约束在SINS/OD系统故障检测中的应用［J］.中国惯性技术学报，2013，21（3）：406-410.

［11］Korsun O N，Poplavskii B K.Estimation of Systematic Errors of Onboard Measurement of Angle of Attack and Sliding Angle Based on Integration of Data of Satellite Navigation System and Identification of Wind Velocity［J］.Journal of Computer and Systems Sciences International，2011，50（1）：130-143.

［12］Sahawne L R，Al-Jarrah M A，Assaleh K，et al.Real-Time Implementation of GPS Aided Low-Cost Strapdown Inertial Navigation System［J］.Intell Robot System，2011，61：527-544.

［13］杨鹏翔，秦永元，周琪，等.基于欧拉角微分模型的捷联惯导直接非线性对准方法［J］.传感技术学报，2011，24（3）：386-391.

［14］魏喜庆，宋申民.基于容积卡尔曼滤波的卫星姿态估［J］.宇航学报，2013，34（2）：193-200.

［15］Gadsden S A，Al-Shabi M，Arasaratnam I，et al.Combined Cubature Kalman and Smooth Variable Structure Filtering：A Robust Nonlinear Estimation Strategy［J］.Signal Processing，2014，962：90-299.

杨理践（1957-），男，教授，博士生导师，主要研究方向为长输油气管道内检测技术及相关理论、无损检测技术等，yanglijian888@163.com；

李 晖（1968-），女，副教授，主要研究方向为长输油气管道内检测技术及相关理论、信号处理技术等，lihui@sut. edu.cn。

The Pipeline Defect Location Technology Based on Cubature Kalman Smooth Filter*

YANG Lijian，LI Hui*，ZHOU Funing，JIN Peng
（ShenYang University of Technology，ShenYang 110870）

Aiming at problems of navigation parameter endurance divergence of pipeline measurement system based on MEMS inertial components for long distance due to more difficult to access effectively to GPS information for correcting navigation errors in submarine pipeline.The cubature kalman smooth algorithm is put forward.The algorithm composes of two stage filters，one is the forward cubature kalman filter based on velocity difference between odometer wheel speed and navigation speed difference and second stage filter is backward kalman smooth filter with final reference points of pipeline measurements displacement being starting point of this stage filter to achieve the optimal estimation of pipeline defect geography coordinate.The results of pipeline geographical coordinates measurement experiments show that this method can effectively compensate the long-time navigation parameter errors，The measurement accuracy for 10 km long pipeline can reach the order of magnitude of 10-3that can meet the precision requirement of the pipeline detection location.

integrated navigation system；pipeline location；cubature kalman filter；smooth filter；locating error correction EEACC：7230

TP274.5

A

1004-1699（2015）04-0591-07

10.3969/j.issn.1004-1699.2015.04.023

项目来源：国家高技术研究发展计划863项目（2012AA040104）；科技部国家重大仪表专项项目（2012YQ090175）；十二五国家科技部支撑计划项目（2011BAK06B01-03）

2014-11-17 修改日期：2015-01-10