基于角度的HDE算法在室内行人航迹定位中的研究

楼喜中，周乐宇，叶敏展，贾一展，金 宁

（1.中国计量学院信息工程学院，杭州 310018；2.中国电信股份有限公司浙江分公司，杭州 310040）

基于角度的HDE算法在室内行人航迹定位中的研究

楼喜中1*，周乐宇1，叶敏展2，贾一展1，金 宁1

（1.中国计量学院信息工程学院，杭州 310018；2.中国电信股份有限公司浙江分公司，杭州 310040）

针对现有启发式偏移消除算法HDE（Heuristic Drift Elimination）中航向角推算不准确、反馈系数鲁棒性较差的问题，提出了对经过扩展卡尔曼滤波的航向角进行启发式漂移消除的算法AHDE（Angle Heuristic Drift Elimination）。首先利用扩展卡尔曼滤波EKF（Extended Kalman Filter）融合陀螺仪、加速度信息，通过四元数的更新来估计航向角，再用启发式漂移消除算法对航向角进行修正，最后结合步数及步长信息推算出行人的行走轨迹。实验结果显示，在行走方向较为固定的典型室内环境中，行走距离在250 m时，该算法平均误差不超过2 m，而HDE算法误差会达到4 m左右。并且该系统具有比对陀螺仪数据进行启发式漂移消除系统更强的鲁棒性。当以100 Hz频率读取数据时，AHDE算法反馈系数的选择范围由HDE算法的［0.001，0.028］扩展为［0.005，0.23］，几乎扩大了一个数量级。

轨迹推算；启发式漂移消除；扩展卡尔曼滤波；计步器

在现代生活中，人们对定位与导航的信息需求日益膨胀，在GPS等卫星定位技术不能使用的室内环境中，基于惯性测试单元IMU（Inertial Measure U-nit）的室内导航技术应用越来越广泛。Levi和Judd 在1996年首次提出了行人航迹推算 PDR （Pedestrian Dead Reckoning）的概念［1］，主要是根据陀螺仪数据计算航向信息，再基于行人步态的运动特征，利用加速度计信息估计步数和步长，结合这3个信息来推算行人的位置和姿态等信息。Johann等人则在PDR模块的基础上提出了更为精确的室内行人轨迹的启发式漂移消除推算算法 HDE （Heuristic Drift Elimination）［2］。该算法主要指出约99%的建筑都有4个或8个主要行进方向，在这种室内环境中，前一时刻的航向角和主要行进方向间的偏差可以用来构成一个反馈系统，再利用反馈参数对陀螺仪数据进行修正，以达到修正航向角的目的。文献［3］继续根据室内环境行进方向较为固定这一特点，提出了改良式的启发式漂移消除算法（iHDE），主要是通过对姿态角和主方向进行卡尔曼滤波以更新最后人体的姿态信息。

在本文中，我们提出了对经过扩展卡尔曼滤波的航向角进行启发式漂移消除的算法——AHDE。该算法在计算航向角时引入了加速度信息以提高准确性，同时，该算法也提高了系统的鲁棒性。不过，和HDE算法相同，AHDE算法也是根据室内环境中行进的几个主方向来对航向角进行修正，因此，在一些歌剧院、室内运动场等空旷环境中，轨迹追踪效果也会相应减弱。本文主要结构安排如下：第二章在HDE算法框图的基础上，提出了存在的一些缺点，并介绍了AHDE算法的模型框图；AHDE算法的具体实现则在第3章中进行叙述；第4章中，我们通过实验来验证算法的有效性；最终在第5章给出结论。

1 算法模型

图1 角速度启发式漂移消除系统框图

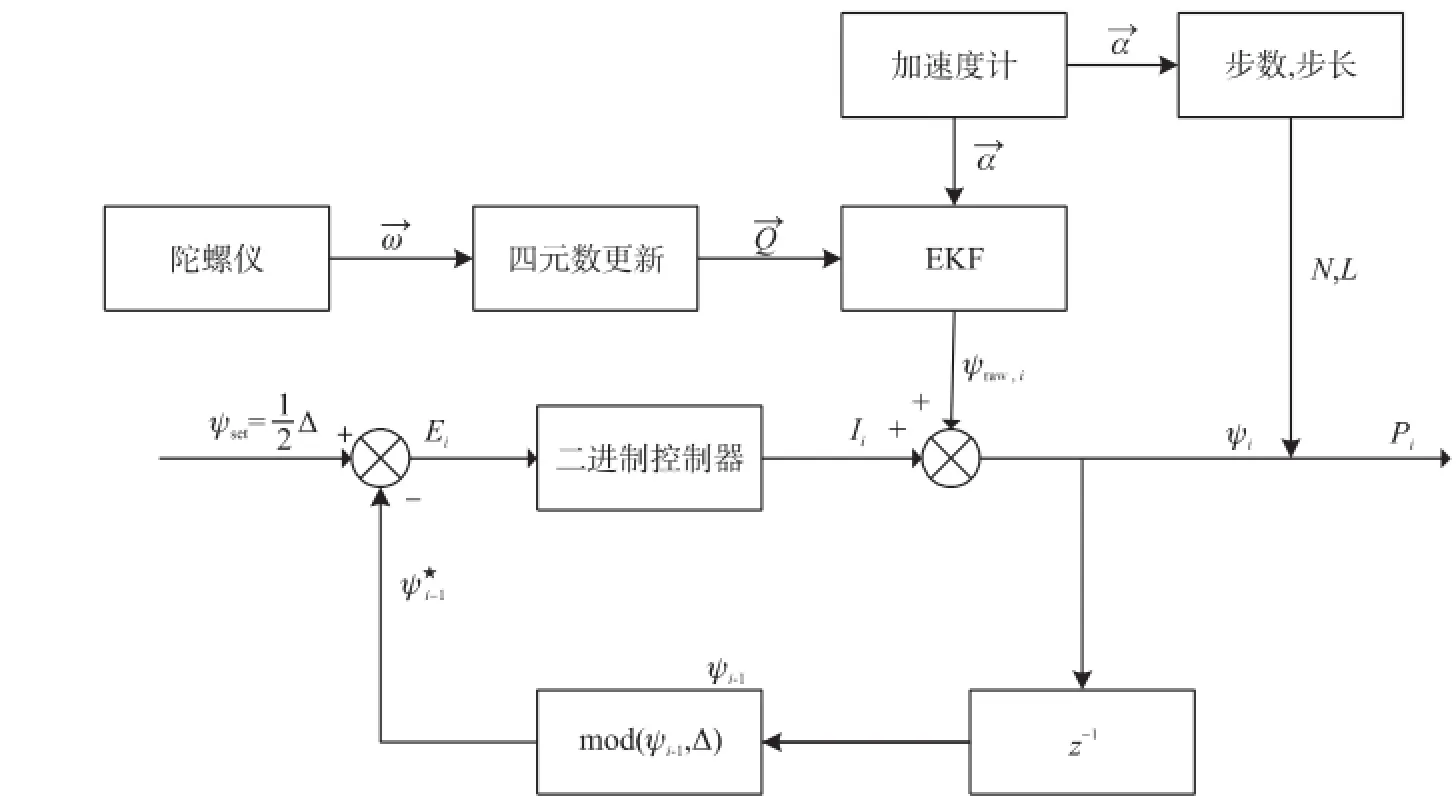
图2 系统总体框

本文提出的算法AHDE的主要框图如图2所示，为了解决上述算法的问题，系统首先利用陀螺仪信息更新四元数，以加速度信息为观测值利用扩展卡尔曼滤波对四元数进行修正，由修正后的四元数可以解算出行人当前的航向角。接着系统通过启发式漂移消除算法中的反馈环对航向角进行修正。同时，根据行人行进过程中的加速度信息，我们可以解算出人体的计步信息和步长信息。最后，修正后的航向角信息结合计步信息、步长信息就可以确认人体当前的位置信息，从而进行室内行人轨迹追踪。

2 算法的实现

2.1 步数检测和步长估计

随着人体的走动，加速度计各轴数据会呈现出具有波峰波谷的震荡波形，通过对这些波形的分析，我们可以判断出人体是否在行进过程中。目前，基于这种传感器的计步检测方法有很多种，本文主要采用基于中间阀值穿越的计步算法［4］。算法的主要包含两个步骤：首先检测到一个从峰值到谷值穿越的一个过程，则被暂定为完整的一步；再对约束条件进行判断，如果在这一步中加速度穿越了中间阈值，并且加速度峰峰值大于一定的阀值，那么就可以确认为完整的一步。

对于步长估计，本文采用了文献［5］中提及的步长估计算法。这种算法主要是针对不同个体选取不同的标定系数，利用实时步频信息对步长进行估计。

式中：L为步长；fstep为实时步频；K1，K2为针对不同个体而标定的系数。

2.2 航向角推算

文献［6］中讨论了姿态解算过程中误差的主要来源，而陀螺仪的随机漂移误差就是其中来源之一。因此，只根据陀螺仪数据来计算航向角会造成较大误差。

目前，用卡尔曼滤波算法结合四元数来更新姿态角的算法已经日益成熟［7-10］。本文将误差四元数作为状态量进行卡尔曼滤波，引入加速度信息作为观测值，可以有效地修正陀螺仪输出量中的随机漂移分量，算法具体步骤如下：

第一步，在初始时刻，我们定义3个姿态角均为0°，并利用如下公式对四元数进行初始化：

式中：q0，q1，q2，q3为四元数；ψ，θ，γ分别为航向角，俯仰角，横滚角。

第二步，当陀螺仪数据更新后，用毕卡三阶算法［11］进行四元数的更新：

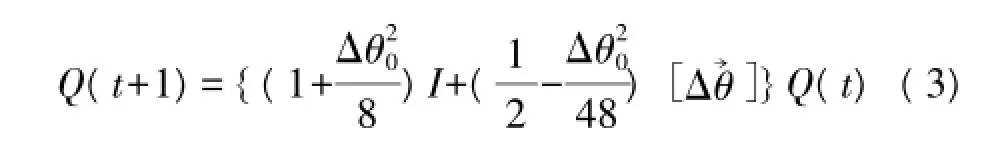
式中：Q（t）为t时刻的四元数，I为单位矩阵，Δθ20为3个轴的角度平方和，Δ→θ为对机体坐标系相对地理坐标系的旋转角速度的斜对称矩阵的积分。

第4步，对四元数进行扩展卡尔曼滤波.本文不对扩展卡尔曼滤波展开详细叙述，详细过程可以参考文献［12-13］。在扩展卡尔曼滤波的时间更新方程中，先验估计状态量和先验估计协方差分别为：

式中：X（k|k-1）为先验估计状态量，在这里初始化为0，P为协方差矩阵，Q为过程噪声矩阵。接下去是状态更新方程，包括卡尔曼增益：

式中：H，R分别为测量雅克比矩阵和观测噪声协方差矩阵。

状态向量更新：

式中：X（k|k）为更新后的状态量，在这里是误差四元数ΔQ，而Z（k）为加速度计的测量值与实际加速度的差值。

协方差矩阵更新：

式中：P（k|k）即为更新后的协方差。

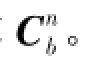
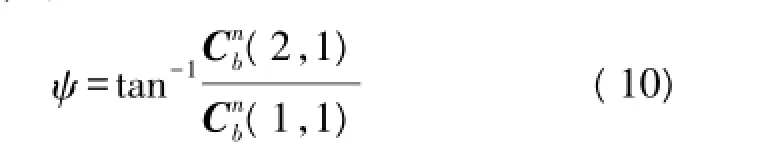
2.3 对角度的启发式漂移消除

从系统总体框图中，我们可以看到，启发式漂移消除算法的核心思想是采用了一个反馈系统，利用前一时刻的航向角对当前时刻的航向角进行修正。主要步骤如下：

第1步，我们需要建立坐标系，也就是设定主方向。一般来说，主方向可以设定为4个或8个，在本文中，我们设定了4个主方向，因此，主方向间的角度间隔Δ为90°。而每次初始时刻前进的方向即为我们所定义的0°方向，其余3个方向则分别为90°，180°，270°。

第2步，在反馈回路中，前一时刻航向角ψi-1相对于当前主方向的偏移角以及偏移方向可以用MOD函数来求取。根据MOD函数的定义：

MOD（n，d）=n-dINT（n/d）

其中，INT（k）为取整函数，结果为不大于k值的最大整数。所以MOD函数的结果在区间［0，d］中。将ψi-1，Δ代入MOD函数，即：

不同的偏移方向，所以接下去的二进制控制器就可以通过判断Ei的正来决定修正的方向。当Ei大于0的时候，则表明航向角方向往左偏移，我们就要对反馈变量Ii减去修正常数ic，使得航向角方向修正回当前主方向；如果Ei小于0，则表明航向角方向往右偏移，我们就要对反馈变量Ii加上修正常数ic，使得航向角方向修正回当前主方向。Ei经过二进制控制器后，我们可以确定当前时刻的反馈系数Ii，即：

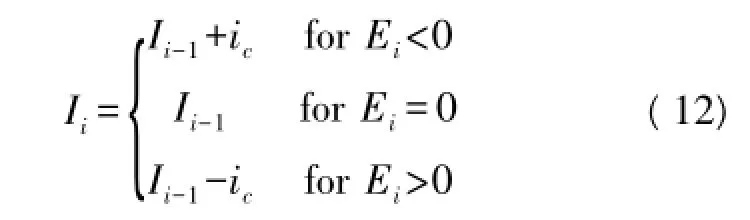
其中ic为常数。

第4步，在得到Ii后，对当前的航向角进行修正，即：ψi=ψraw，i+Ii。最后结合步态信息和航向角信息确定人体当前的位置信息：

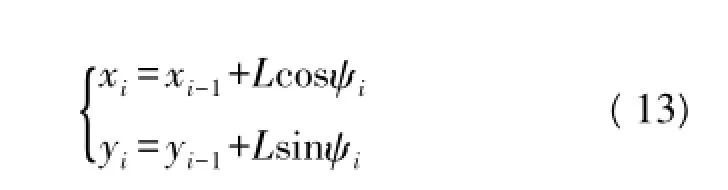
3 实验与结果

为了验证所提算法的有效性，本文以包含MPU6050传感器的模块进行试验。将模块固定在鞋子上，并以100 Hz的频率读取陀螺仪，加速度计的数据。

首先，我们绕着一个正方形建筑转一圈，测试结果如图3所示。

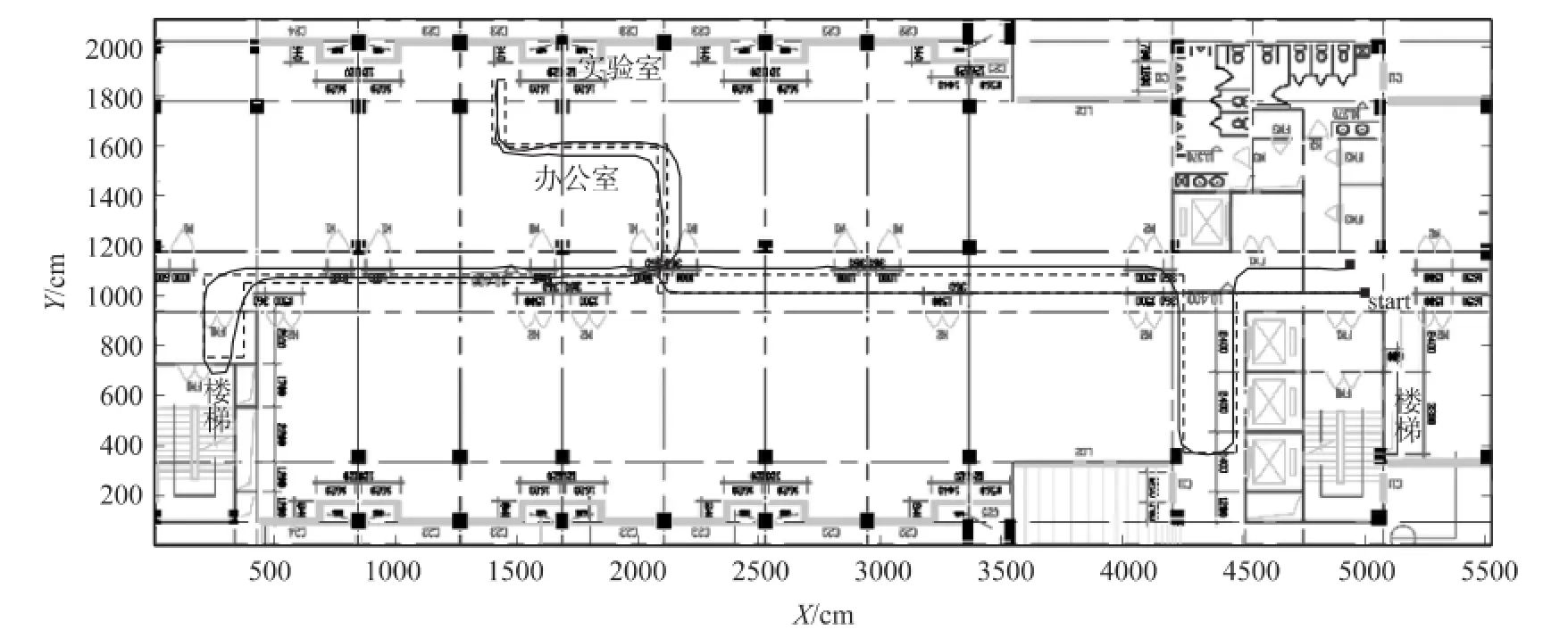
图4 楼层内部行走测试图

图3中，黑色实线表示实际行走路线，并且起点和终点重合；虚线表示利用扩展卡尔曼滤波后的航向角进行轨迹推算的结果；带倒三角实线表示HDE算法的轨迹推算结果；带加号标记实线表示AHDE算法的轨迹推算结果。我们可以看到，由于陀螺仪误差，最后两个转弯时，航向角转动幅度无法达到实际的90°，从而偏离实际轨迹，而利用航向角直接进行轨迹推算存在较大的误差，再经过启发式漂移消除算法后，最终误差大大减小，最终测试位置与实际位置误差为1.9 m。

为了检验该算法在复杂行走轨迹中的效果，我们在一幢建筑物4楼内部进行了更为复杂的行走。测试结果如图4所示。图4中，黑色虚线表示实际行走路线，起点和终点重合；实线表示根据AHDE算法得出的轨迹推算结果。最终测试位置与实际位置误差为1.6 m。

为了检验系统的鲁棒性，主要是看反馈系数对系统造成多大的影响，我们对同一组数据采用不同的反馈系数进行仿真，结果如图5所示。

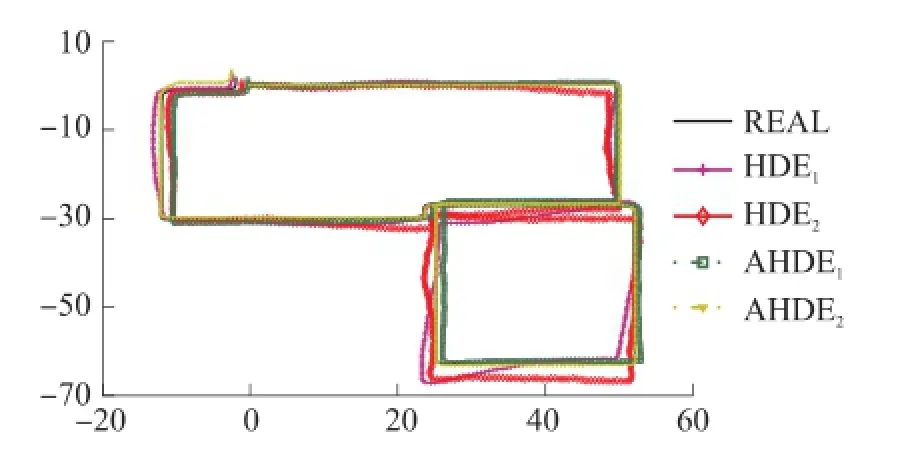
图5 反馈系数测试

图5中，起点为坐标原点，带六边形实线和带加号标记实线分别是系数为 0.001、0.028时，利用HDE算法进行修正后的结果。在0.001和0.028这两个极值处，行进过程中和真实轨迹最大误差分别为3.7 m、4.9 m；当系数小于0.001或大于0.028，误差会大幅增大。带正方形标记实线和带倒三角标记虚线分别是系数为0.005、0.23时，利用AHDE算法进行修正后的结果。在0.005和0.23这两个极值处的最大误差分别为2 m、2.5 m；当系数小于0.005或大于0.23，误差也会大幅增大。黑色实线为真实轨迹。可以看到，在可接受精度范围内AHDE算法中反馈系数的可变区间比HDE算法几乎提高了一个数量级。因此，该算法对反馈系数的选择有更宽的范围，有效地提高了系统的鲁棒性。

4 结论

本文利用陀螺仪数据更新四元数，并利用加速度信息作为观测量，对四元数进行扩展卡尔曼滤波，最终用四元数推算出航向角，减少了原来利用陀螺仪数据直接求取航向角的误差。

在对陀螺仪数据进行启发式漂移消除过程中，由于陀螺仪的数据首先要经过双重低通滤波，因此，反馈系数的轻微改变就会对修正结果造成很大的影响，降低了系统的鲁棒性。而本文提出的系统对反馈系数的选取要求并没有十分严格，提高了系统的鲁棒性。并且经过多次测试，最终的推算位置与实际位置误差不超过2 m。

在接下去的工作中，我们将在AHDE的基础上融合地图信息，这样可以避免穿墙等错误情况出现；除此之外，我们还将改进该算法使其更好地适应圆形等不规则轨迹，并且还可以导入磁力计信息来提高航向角的准确度。

［1］ Levi Robert W，Judd Thomas.Dead Reckoning Navigational System Using Accelerometer to Measure Foot Impacts［P］.US，5583776. 1996-12-10.

［2］ Johann Borenstein，Lauro Ojeda.Heuristic Drift Elimination for Personnel Tracking Systems［J］.The Journal of Navigation，2010，63（4）：591-606.

［3］ Jimenez A R，Seco F，Zampella F，et al.Improved Heuristic Drift Elimination（iHDE）for Pedestrian Navigation in Complex Buildings ［C］//Indoor Positioning and Indoor Navigation（IPIN）.Guimaraes：IPIN，2011：1-8.

［4］ Zhao N.Full-Featured Pedometer Design Realized with 3-Axis Digital Accelerometer［J］.Analog Dialogue，2010：44（6）：17-21.

［5］ 申崇江，冯成涛，崔莹，等.穿戴式室内行人航位推算系统研究［C］//第五届中国卫星导航学术年会，2014.

［6］ Qin Li，Zhang Huixin，Xu Weixing.Optimizing Algorithms of the Attitude of the Flying Objects［J］.Sensors，Proceeding of IEEE，2004（2）：927-930.

［7］ 张荣辉，贾宏光，陈涛，等.基于四元数法的捷联式惯性导航系统的姿态解算［J］.光学精密工程，2008，16（10）：1963-1970.

［8］ 叶锃锋，冯恩信.基于四元数和卡尔曼滤波的两轮车姿态稳定方法［J］.传感技术学报，2012，25（4）：524-528.

［9］ 邹波，张华，姜军.多传感信息融合的改进扩展卡尔曼滤波定姿［J］.计算机应用研究，2014，，31（4）：1035-1038.

［10］秦永元.惯性导航［M］.北京：科学出版社，2006：14-164.

［11］邓正隆.惯性技术［M］.哈尔滨：哈尔滨工业大学出版社，2006：140-180.

［12］殷红.基于foot-mounted的IMU室内行人航迹推算研究［D］.南昌：南昌大学理学院，2013.

［13］贾瑞才，基于四元数EKF的低成本MEMS姿态估计算法［J］.传感技术学报，2014，27（1）：90-95.

楼喜中（1976-），男，中国计量学院副教授，2005年获得哈尔滨工业大学微电子学与固体电子学博士学位，主要研究方向为无线定位、MEMS传感器导航定位、多天线技术、信道编码技术等。

Researching on Indoor Pedestrian Trajectory Based on Angle HDE Algorithm

LOU Xizhong1*，ZHOU Leyu1，YE Minzhan2，JIA Yizhan1，JIN Ning1
（1.College of Information Engineering，China Jiliang University，Hangzhou 310018，China；2.China Telecom Co Zhejiang branch，Hangzhou 310040，China）

The Heuristic Drift Elimination（HDE）algorithm has disadvantages such as the inaccurate heading angle and poor robustness，the AHDE algorithm was proposed which implementing Heuristic Drift Elimination based on heading angle with Extended Kalman Filter.The heading angle is renewed by Quaternion which is achieved from the integration of gyroscope data and accelerometer data.After updating the heading angle with the algorithm of Heuristic Drift Elimination，the angle can be used to reckon the pedestrian trajectory combined with step number and stride length.The experimental results show that，when walking in typical structured indoor environments，the error of the proposed algorithm is less than 2 m in 250 m distance，and the error of the HDE algorithm is 4 m roughly.On the other hand，when the sampling data rate of the sensors is 100Hz，the convergence range of feedback coefficient of the AHDE system can be extended to［0.005，0.23］，however the range of the HDE system is［0.001，0.028］.That is to say the AHDE system is more robust than the HDE system.

reckon trajectory；heuristic drift elimination；extended Kalman filter；pedometer EEACC：2575

TN96

A

1004-1699（2015）04-0598-05

10.3969/j.issn.1004-1699.2015.04.024

2014-11-19 修改日期：2014-12-30