球面立体视觉系统参数标定与极线校正方法研究

龙帮强 鲁春芳 冯为嘉

（1.天津大学精密测试技术及仪器国家重点实验室 天津 300072 2.天津工业大学电子与通信工程学院 天津 300387 3.天津理工大学天津市复杂工业系统控制理论及应用重点实验室 天津 300384 4.天津师范大学计算机与信息工程学院 天津 300387）

1 引言

鱼眼镜头具有短焦距，大视场的特点，一次拍摄可以捕获 185°×185°视场内的全部信息，大量文献证明鱼眼镜头建立的多视系统比传统的透视投影立体视觉系统能得到更大的三维视场[1]。鱼眼镜头及图像如图1所示。所涉及的应用包括城市形貌及景物三维重建、森林树木检测、无人驾驶机、移动机器人导航及辅助驾驶等[2-3]，利用双鱼眼镜头构建的立体视觉系统被称为“Spherical Stereo Vision System”—球面立体视觉[1]。其研究工作本质是讨论球面模型下的立体视觉方法。球面模型建立的过程可以视为鱼眼镜头成像的逆过程，由于投影方程是可逆的，因此图像上的每一点都可以经过一条通过投影中心O的射线与球面相交，在球面模型下，整幅图像将被映射到一个单位球上。因此球面模型就具有描述360°视场角的特性。然而，球面立体视觉系统的应用有两个重要的基础：①系统参数标定。包括成像系统自身的内部参数和用于描述刚体变换的外部参数[4]；②两幅鱼眼图像的极线校正，目的在于降低后续匹配过程的复杂度，提高匹配精度。

图1 鱼眼镜头及鱼眼图像Fig.1 Fisheye lens and fisheye image

系统的参数标定可以确定世界坐标系与图像坐标系间的映射关系[5]。精确的参数标定能够为极线校正提供基础矩阵计算过程中所需相关参数。面向针孔相机模型的参数标定方法国内外已取得丰硕的研究成果[6]，而对于基于鱼眼镜头建立的立体视觉系统的参数标定方法的研究工作则鲜有报道[1]。

极线几何用于描述立体视觉系统中不同相机两幅图像间的对应关系[7]。在立体匹配前进行极线校正是必要的，目的在于建立理想的立体视觉系统架构，消除垂直方向的视差，从而降低立体匹配过程中的计算复杂度。极线校正使得同一空间点在两幅图像上的投影位于同一极线上，从而使匹配时的搜索范围从二维（X方向和Y方向）降低到一维（仅X方向）提高了匹配效率[8]。但是，由于球面立体视觉系统采用双鱼眼镜头构建，使得其极线几何与常规立体视觉不同，呈非线性，具有开展研究的必要。

2 球面立体视觉系统几何与数学建模

2.1 几何模型

对于球面立体视觉系统几何模型，本文将从鱼眼镜头光轴相互平行和相互垂直两种情况进行讨论。图2为光轴相互平行时球面立体视觉的几何模型。图3为光轴相互垂直时球面立体视觉的几何模型。两个模型均由世界坐标系，摄像机坐标系，图像坐标系，成像芯片坐标系构成。模型中描述了空间中任意一点在球面立体视觉系统成像的一般情况。每部相机的性质将由需要标定的内部参数来描述，两部相机间的位姿关系将通过外部参数来关联。球面立体视觉系统的特性将由需要标定的内部外部参数共同描述。

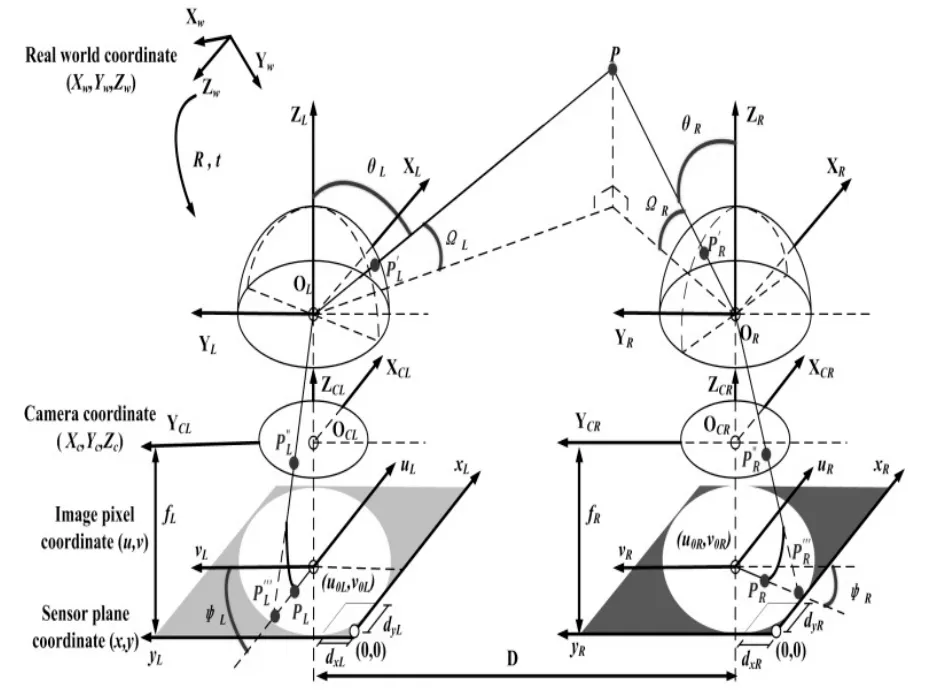
图2 光轴相互平行的球面立体视觉几何模型Fig.2 Geometric model of Spherical Stereo Vision System with paralleled optical axises

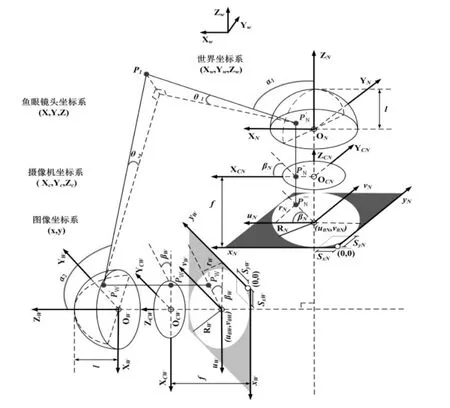
图3 光轴相互垂直的球面立体视觉几何模型Fig.3 Geometric model of Spherical Stereo Vision System with verticaled optical axises

2.2 球面立体视觉系统内部参数数学模型

通常情况下鱼眼镜头均是根据等立体角投影、等距投影、体视投影或正交投影的其中一种模型所设计制造的。若能提出一种可以概括以上四种模型的通用鱼眼镜头数学模型，具有重要理论价值。本文利用式（1）对四种鱼眼镜头投影模型进行拟合

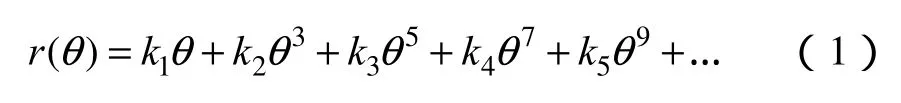
当只取式（1）中前五项时，θ 的次数已经达到9次，这时式（1）已可以近似拟合以上4种投影模型的投影曲线。因此该视觉模型仿射对称部分包括5个参数：k1，k2，k3，k4，k5。为了使球面立体视觉系统的数学模型对于多数鱼眼镜头更具通用性，设F(β)为入射光线到图像坐标上的映射

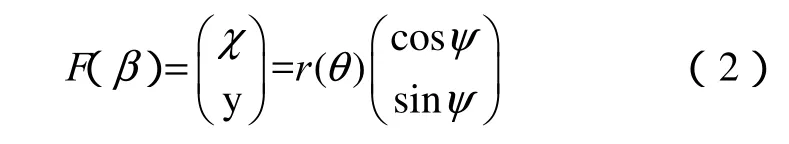
其中，r(θ)包括了式（1）中的前五项，θ则是入射光线与主光轴夹角。β =（θ，σ）T表示为入射光线的方向。为了该模型更具广泛应用，引入以下两种畸变模型。

一种是径向畸变

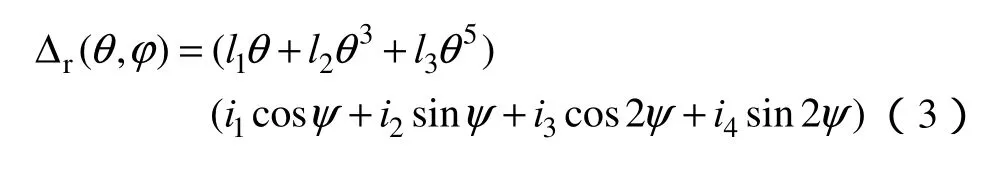
另一种是切向畸变

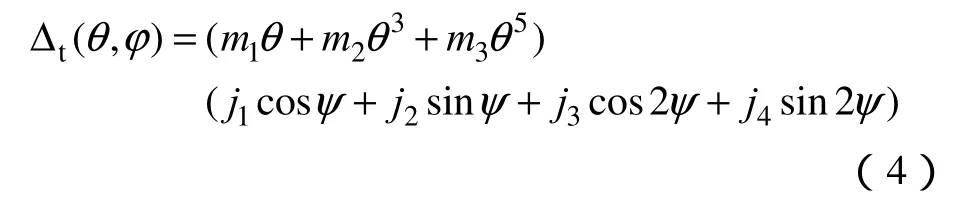
将式（3）和式（4）两种畸变模型引入到式（2）中便可得到畸变坐标如下

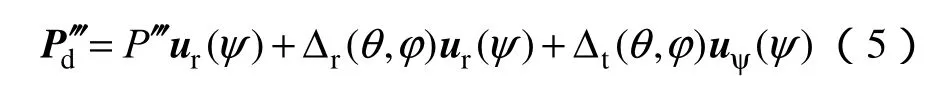
式中，ur(ψ)与uψ(ψ)分别表示径向与切向方向上的单位向量。

为了获得完整的视觉系统模型，我们还需要将成像芯片平面坐标转换到图像像素坐标=(u.v)T。假设转化矩阵正交，则可得到转换关系如下

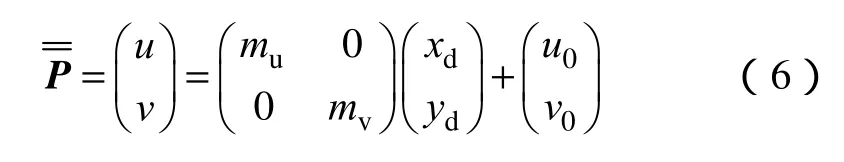
式中，(u0,v0)T为图像中心； mu和 mv分别表示在水平和垂直方向上的单位距离内的像素点的个数。该系统通用数学模型包含23个待标定参数。由于相机内部参数描述相机的性质，因此不同位姿下，相同相机的内部参数依旧相同。

2.3 球面立体视觉系统外部参数数学模型

对于球面立体视觉系统中任意鱼眼镜头的坐标系与世界坐标系的位置关系空间可以用变换矩阵M表示为

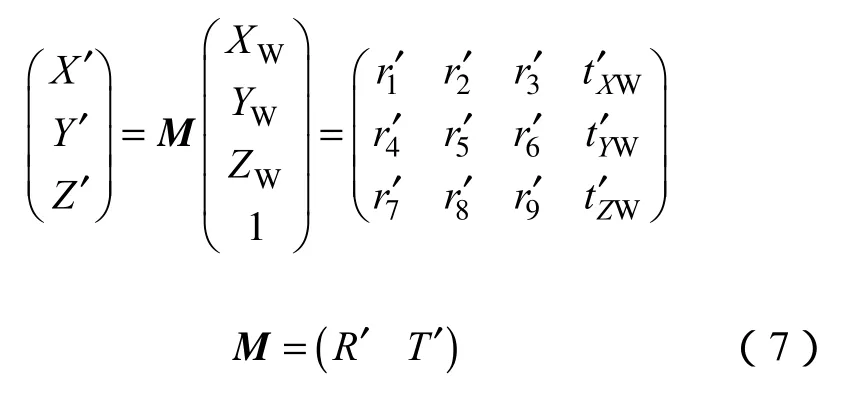
假设空间中任意一点 P，在世界坐标系、球面立体视觉系统中的鱼眼镜头A的坐标系和鱼眼镜头B的坐标系中分别成像且其非其次坐标分别为XW，XA和XB，则有

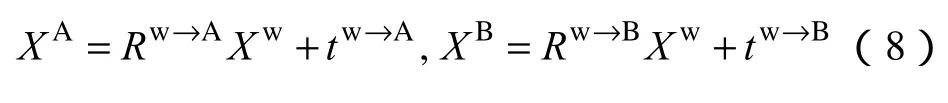
消去XW，可得

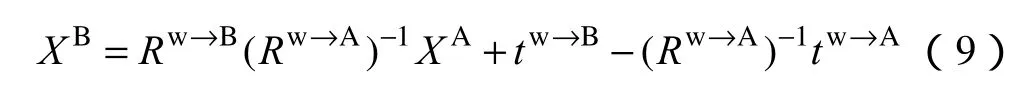
两个相邻鱼眼镜头间的位姿关系可以表示为

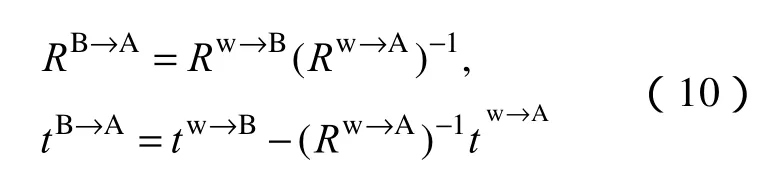
据此，我们可以得到其他镜头间的几何关系如RA→B,tA→B,RB→C,tB→C,RC→D,tC→D至此以上则为球面立体视觉系统的外部参数。系统外部参数确立了两部相机间的位置关系，因此光轴水平和光轴垂直两种位姿关系下的球面立体视觉系统外部参数不同。

2.4 球面立体视觉系统内外参数标定结果

本文采用两支鱼眼镜头 FE185C046HA-1和两台 UC-1830-CL-12B摄像机构建球面立体视觉系统仿真平台。以光轴互相垂直为例，图4为建立的系统仿真平台，图5为该仿真平台两部相机分别拍摄的靶标图像。

图4 球面立体视觉系统仿真平台Fig.4 The simulation platform of SSVS

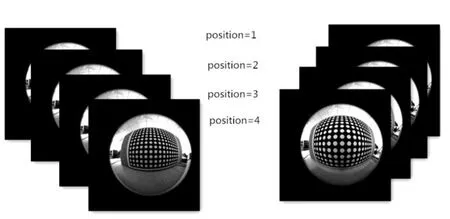
图5 靶标图像Fig.5 The images of calibration pattern

本文采用适用于鱼眼镜头等畸变较大镜头的平面特征圆靶标。假设摄像机内部参数不随摄像机或靶标的运动而改变，通过在不同位置所拍摄的多幅靶标图像建立每个特征点（特征圆圆心）与其图像上像点之间的对应关系的方法进行相关参数标定。表1和表2为球面立体视觉系统参数标定结果。图6和图7以三维空间的形式展示了仿真系统对4幅不同位资的靶标定结果。由图中可以看出，两部相机间Z轴相互垂直，X、Y轴彼此相互平行。从仿真图中可以看出标定结果符合现实空间中的位姿。

表 1 球面立体视觉系统垂直位姿下内部参数标定结果Tab.1 Estimated calibration parameters with paralleled optical axises

表2 球面立体视觉系统平行位姿下内部参数标定结果Tab.2 Estimated calibration parameters with verticaled optical axises

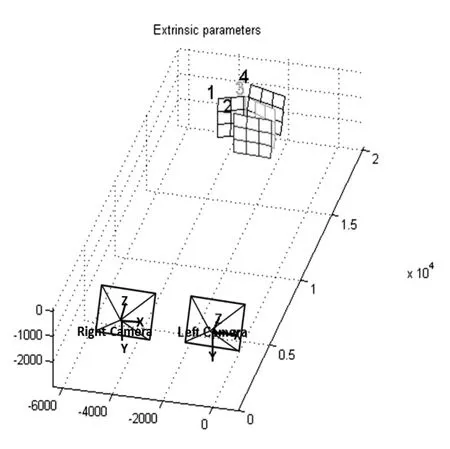
图6 相机与靶标间的空间平行位置关系Fig.6 The relationship of paralleled optical axises SSVS and partterns in 3D space

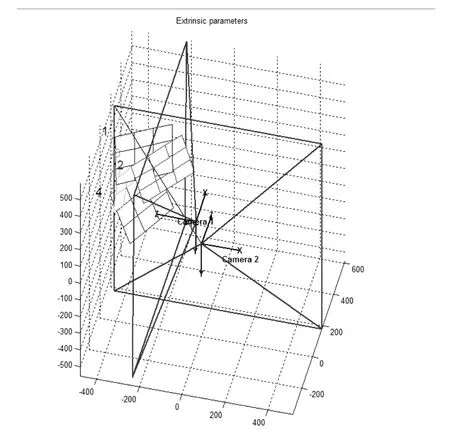
图7 相机与靶标间的空间垂直位置关系Fig.7 The relationship of verticaled optical axises SSVS and partterns in 3D space

3 球面立体视觉系统极线校正方法

3.1 球面成像模型

对于立体视觉的研究绝大多数都是基于透视投影模型。然而，透视投影模型仅适用于 120°左右的视场角的鱼眼镜头。对于视场角接近 180°的鱼眼镜头，去畸变后转化成透视投影模型之后的图像尺寸将接近于无穷大，因此在有限的像素尺寸中将不可避免地存在信息丢失的情况。

相对于透视模型而言，球面投影模型可以对大视场图像更好的描述。球面模型的建立可以视为鱼眼摄像机成像的逆过程。图像上的成像点根据标定后得到的投影方程反投影到球面上，然后在前面之上建立相应的球面图像。在球面图像中，空间直线不再为图像平面的直线而是球面上的弧线。球面模型相对于透视投影，能够表示入射角更大的成像情况。

3.2 极线校正原理

极线校正可以定义为将一对图片转换到特定位置的几何转换，该特定位置可以使得空间中同一点在两幅图像上的成像均位于同一直线上。极线校正的目的是建立理想的立体视觉架构，从而降低立体匹配过程中的计算难度。而理想的立体视觉架构首先满足两部摄像机内参的一致性，其次两个摄像机间还要符合特定的位置关系。

极线校正过程可以认为是一个二次投影过程，即将空间三维点投影到虚拟的相机平面上。该虚拟相机平面具有以下理想特性：光轴平行，相同的内部参数，不失真。图8展示了真实相机成像面与虚拟相机成像面间的关系。

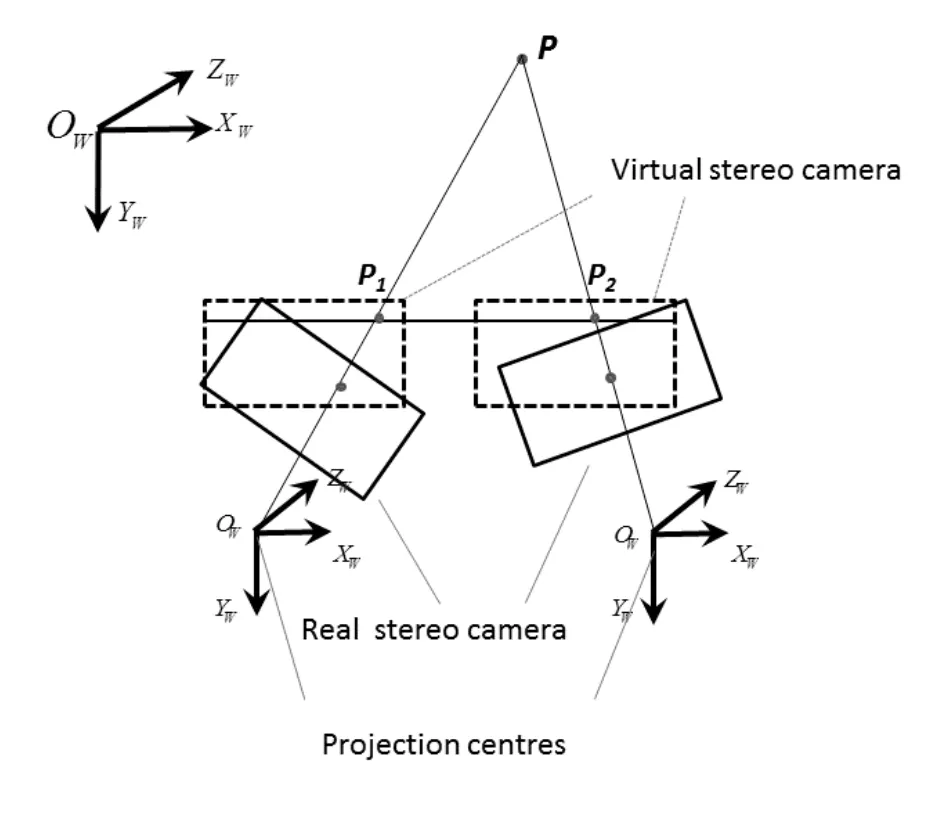
图8 立体视觉极线校正模型Fig.8 The model of real and virtual stereo camera

3.3 球面立体视觉系统极线校正方法

与透视立体视觉极线校正模型相同，球面立体视觉同样需要两个及以上的不同视角的球面模型对场景进行观测。由于球面立体视觉系统中相邻两部相机成90°水平安放，因此球面立体视觉系统的极线几何是一种区别于双目立体视觉系统和平行球型立体视觉系统的非线性极线几何。图9示意了球面立体视觉系统的观测过程。

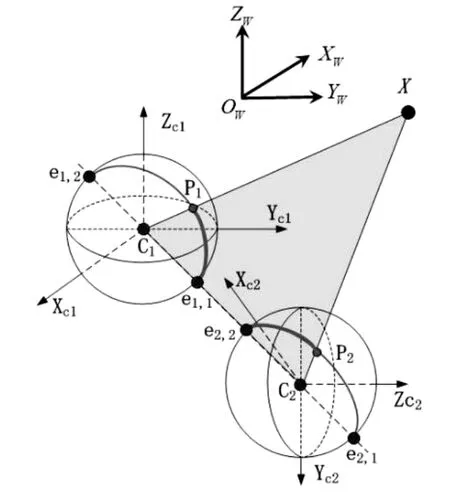
图9 球面立体视觉系统Fig.9 Virtual camera system with fish-eye lens which are perpendicular to each other

在球面模型中的对应点同样需要满足相应的极线约束。设三维场景点X在第一个球面模型中的投影点为P1，在第二个球面模型中的投影点为P2。根据中心投影定理，连个球面模型中心C1，C2与投影点P1，P2以及场景点X共同形成一个极平面。随着场景点的移动，极平面将绕着基线C1C2旋转，这些极平面一同构成极平面束。在透视投影模型下，图像平面与极平面相交于极线 l，不同的极线簇相交于一个基点 e。但在球面模型中，极平面束与球面相交的结果为球面上的大圆，即为球面模型的极曲线，不同的极曲线汇聚于球面模型中的两个极点e1，e2。对应点P1、P2同样满足极线约束

球面立体视觉系统的理想位置为，两部相邻相机成水平90°夹角，即两部相机的3个坐标轴彼此相互垂直如图9所示。但理想立体视觉架构很难实现，因此我们需要通过极线校正来生成满足相应极线约束的虚拟球面模型。世界坐标系下点 Xw=[XwYwZw]，经过旋转矩阵R和平移向量T，变换为县级坐标系下坐标Xc。其中，r1，r2，r3分别为R的3个行向量，对应X，Y，Z 3个相机坐标轴方向。本文的校正方法参考了文献[9]。假设新生成的连个虚拟相机投影模型为

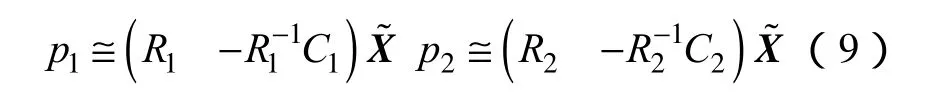
（1）连接两个摄像机的中心，生成一个空间向量，然后依次作为X轴

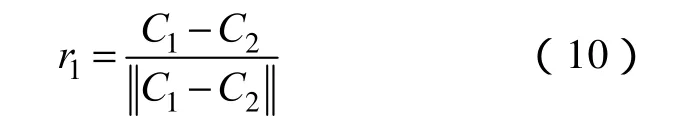
（2）设定一个向量 v，使得 Y轴同时正交与X轴与v：

（3）最后，根据正交坐标系定义，Z轴由X轴和Y轴共同确定

然后再将球面模型上的灰度图投影到校正平面。以下以一个鱼眼镜头举例说明。

假定空间中一点P，其投影点为p1o，校正平面点为p1n，则有

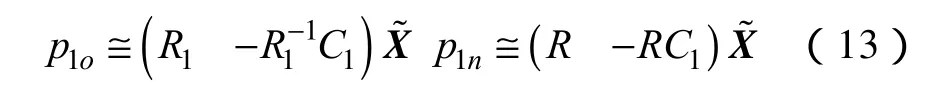
容易得出

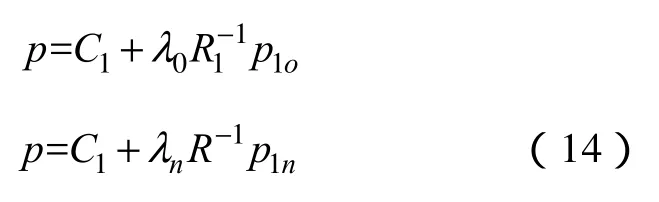
式中，λn和λ0为比例因子。因此我们可以得到

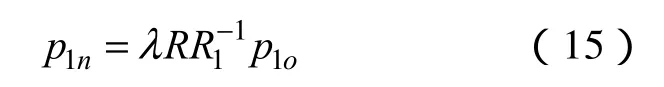
式中，λ=λo/λn。由于球面图像与校正图像有相同的像素值因此λ=1。

3.4 球面立体视觉系统极线校正实验结果

对光轴平行的球面立体视觉拍摄的靶标图像实施极线校正测试。图10a为两部相机同时采集的靶标图像，其像素尺寸为1 024×1 024。利用标定得到的相机的内部参数和外部参数可以对图像进行极线校正。图10b为极线校正后的一对靶标图片，从图中可以看出球面立体视觉系统的极线彼此平行，并且空间中同一点在两幅图像上的像均在同一直线上。

图10 靶标的极线校正图像Fig.10 Rectification of pattern images,Original images,Pair of epipolar rectification image

4 结论

本文研究球面立体视觉参数标定方法，标定得到的内、外参数为极线校正基础矩阵提供所需参数。分别建立了光轴相互平行以及光轴相互垂直两种球面立体视觉系统的几何模型，并提出数学模型描述内、外参数关系。通过拍摄特征圆靶标的形式实施参数标定并给出快速有效的参数标定方法。利用参数标定结果对采集到的一组鱼眼图像实施极线校正。该极线校正方法基于二次虚拟投影，适用于大场景的观测系统。实验结果证明，本文提出的方法实用且有效，有助于球面立体视觉的推广与应用。

[1] Li Shigang,Binocular spherical stereo[J],IEEE Transactions on Intelligent Transportation Systems,2008,9,520-526.

[2] Gehrig S.,Rabe C,Krueger L.6D vision goes fisheye for intersection assistance[J].Proc.Com- puter and Robot Vision',2008,34-41.

[3] Liu Yu Chih,Lin Kai Ying,Chen Yong Sheng,Bird’s-eye view vision system for vehicle surrounding monitoring[J].Robot Vision.2008,(4931),207-218.

[4] Eynard D,Vasseur P,Demonceaux C,et al.UAV altitudeEstimation by mixed stereoscopic vision[J].Intelligent Robots and Systems,2010,17(18),646-651.

[5] Michal Havlena,Tomas Pajdla,Structure from omnidirectional stereo rig motion for city modeling[C].Proc.International Conference on Computer Vision Theory and Applications,2008,407-414.

[6] Nishimoto T,Yamaguchi J.Three dimensional measurement using fisheye Stereo vision[C].Proc.SICE Annual Conference,2007,2008-2012.

[7] Li S,Fukumori K.Spherical stereo for the construction of immersive VR environment[C].Proc.IEEE VR Conference,2005,217.

[8] Henderson D W,Taimina D.Experiencing geometry:euclidean and non-euclidean with history.englewood cliffs,NJ:Prentice-Hall,2005.

[9] Herrera P.J,Pajares G,Guijarro M,et al.A stereovision sensor for forest inventories sensor[J].Device Technologies and Applications,2010,64(117):73-79.