椭偏电磁波在手征负折射介质表面的反射与折射特性研究

崔兴霞 金 毅 宋 朋* 孙晓娟 徐 娟

（济南大学物理科学与技术学院 济南 250022）

1 引言

负折射率材料有许多奇特的特性，如负折射效应、反常Doppler效应、反常Cherenkov辐射及“完美透镜”效应等[1]。正是由于这些独特的特性，最近几年负折射率材料在材料科学、光学、应用电磁学和固体物理学领域受到广泛的关注，对它的研究也成为科学领域的一大热点。

目前，科学家主要以双负方法、传输线方法和光子晶体方法这三种方法利用人工介质实现负折射。在20世纪80、90年代，随着对手征介质的进一步认识以及手征材料制作技术的发展，手征介质在许多领域有了新的应用。最近，Pendry、Tretyakov等提出了利用手征材料实现负折射的新方法[2]。由于手征负折射率介质特性不同于一般介质特性，电磁波在其中的传播与我们常规介质中传播的理论不同。不能用已有的公式分析电磁波在手征介质中的传播，需要对电磁波的行为重新讨论。本文基于电磁波的传输特性、手征负折射率介质中的本构关系及边界条件，从圆偏振电磁波在手征负折射率介质表面的反射和折射入手，讨论了椭圆偏振电磁波在手征负折射率介质表面的反射和折射特性，并通过与经典理论的对比找出了它们的不同。

2 电磁波在手征负折射率介质中的基本理论

手征性是指物体经过平移、旋转等任意空间操作均不能与其镜像完全重合的特性。手征性在光学中主要表现为旋光性和圆二向色性。

介质对电磁波的影响通过本构关系来描述。对双各向同性介质，本构关系中除了通常的介电常数和磁导率之外，还有两个表示电场和磁场交叉耦合的参数。手征介质是双各向同性介质的特例，其电场和磁场的交叉耦合是互易的，此时交叉耦合为同一参数，即手征参数χ。

时谐电磁波在各向同性手征负折射率介质中的本构关系为[3-4]

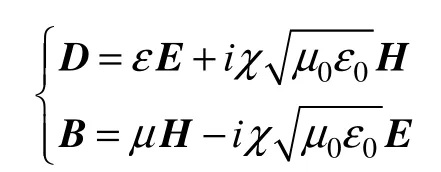
式中，ε为手征介质的介电常数；μ为手征介质的磁导率；ε0为真空中的介电常数；μ0为真空中的磁导率。

在手征介质中，存在两个本征电磁波：右旋圆偏振电磁波和左旋圆偏振电磁波。本征波满足Helmholtz方程

式中，E±、B±分别为右旋圆偏振电磁波和左旋圆偏振电磁波的电场分量和磁场分量（+表示右旋，−表示左旋）。

右旋圆偏振电磁波和左旋圆偏振电磁波的波数为

式中，n±=n±χ为右旋圆偏振电磁波和左旋圆偏振电磁波的有效折射率，表示手征介质的折射率；为真空中电磁波的波数。

当χ＞n时，n−＜0，这样就实现了左旋圆偏振电磁波在手征介质中的负折射。对于左旋圆偏振电磁波E、H、k构成左手螺旋关系，能流密度矢量S与波矢k反向。χ＞n的手征介质就是所谓的手征负折射率介质。

3 椭圆偏振电磁波在手征负折射介质表面的反射与折射

椭圆偏振电磁波可以用左旋圆偏电磁波和右旋圆偏电磁波的叠加来表示，因此我们先分析圆偏电磁波入射时的情况[5]。

如图1所示，圆偏电磁波由常规介质入射手征负折射介质表面时，折射电磁波中的左旋圆偏振分量发生负折射，位于法线另一侧。在图中给定的电磁参数下，入射圆偏电磁波的复振幅表达式如下（设入射电磁波沿y方向振幅分量为1）

图1 电磁波在手征负折射率介质表面的反射与折射Fig.1 The reflection and refraction of EM waves on the surface of the chiral negative refractive index medium

式中，+表示右旋，−表示左旋；θi为入射角，波数。由图1中几何关系可得，kr沿x方向分量为krx=krs inθr，ki沿z方向分量为krz=krzcosθr。

反射波在常规介质中传播，可以表示为TE波和TM波的叠加。根据其在介质1中的传播，以am表示TE波的振幅，以bm表示TM波的振幅（下标m=1表示右旋圆偏振电磁波入射，m=2表示左旋圆偏振电磁波入射）。则反射波电磁场复数表达式为

折射波可用右旋圆偏振电磁波和左旋圆偏振电磁波的叠加表示，（+表示右旋，−表示左旋；m=1表示右旋圆偏振电磁波入射，m=2表示左旋圆偏振电磁波入射）

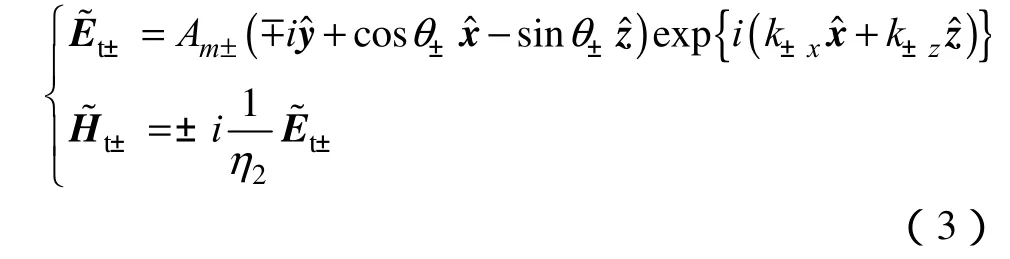
式中，θ±分别表示折射波中右旋圆偏振电磁波和左旋圆偏振电磁波分量的折射角；波阻抗；折射率。

由波矢边界连续条件 kix=krx=ktx，kty=kry=kty，可得到反射定律，θi=θr；折射定律，（n±=n2±χ），对于手征负折射介质χ＞n2（n−＜0），因此θ−＜0。左旋圆偏振电磁波发生了负折射，其折射波与入射波位于法线同侧[6-7]。且E、H、k满足左手螺旋关系。根据电磁波的边界条件推导出复振幅参数

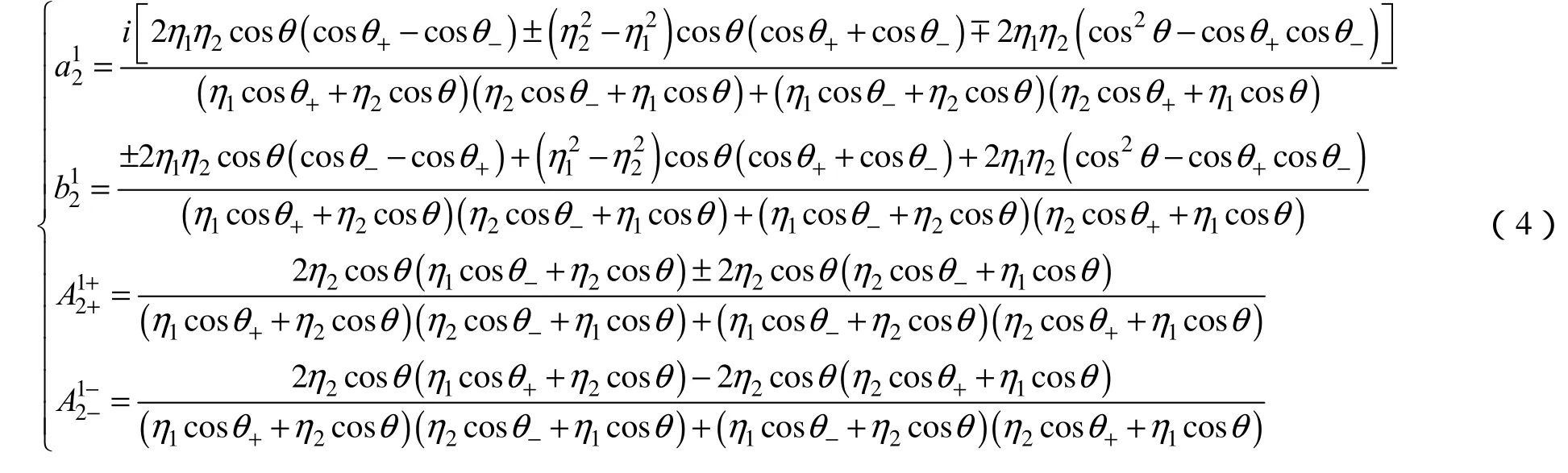
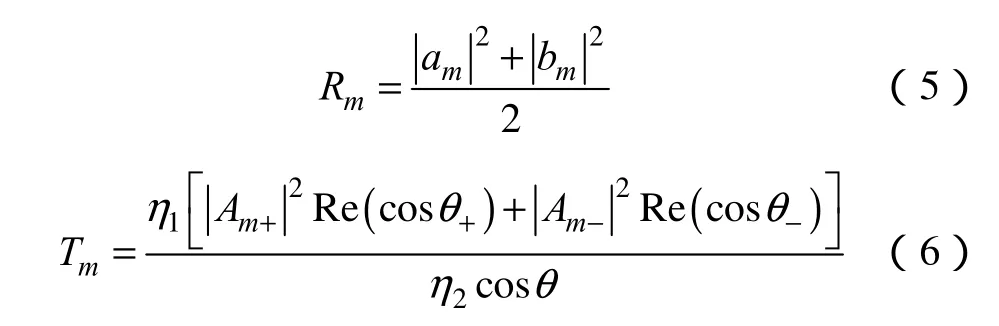
当入射角大于临界角θc±时，折射角θ±为负数角度，透射波变为表面波，透射波离开交界面后迅速衰减，实际上并没有功率透过，因此取折射角的实部，当θi大于θc±时，相应的折射角余弦的实部为零，没有实功率透过，只有虚功率。

由复振幅反射率和折射率可以看出，am和 bm不相等，且存在相位差。因此，反射波为椭圆偏振电磁波。但是，当入射电磁波以某一特定角度θb入射时，反射电磁波能够变成线偏振，am和bm中有一个为零或他们的相位差为零。这个入射角θb就被称为布儒斯特角。

任意的椭圆偏振电磁波都可以通过坐标系的旋转变成正椭圆偏振电磁波，在这里，只讨论正椭圆偏振电磁波入射的情况。设正椭圆偏振电磁波沿方向的电场分量为E1，沿 xOz平面的电场分量为E2。则右旋和左旋正椭圆偏振电磁波入射的电场的复数表达式为

利用单位振幅的圆偏振电磁波可表示为

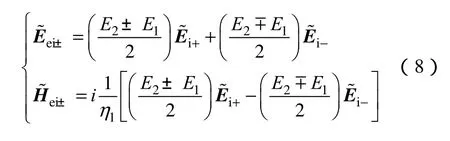
同理得到反射波

透射波

以及能流反射率和透射率

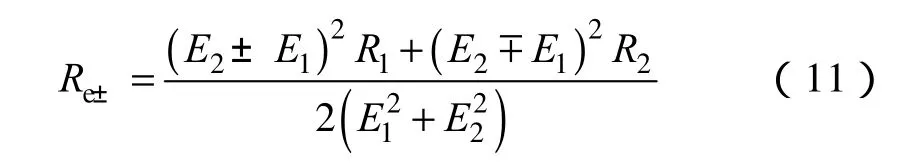
4 数值分析

因任意椭圆偏振电磁波较为复杂，我们仅以E1=1、E2=2的正椭圆偏振电磁波入射的情况为例，对平均能流反射率和透射率，以及全反射的情况进行了讨论。选择介质参数μ1=μ1=μ0，ε1=ε0，ε2=0.16ε0，则n2=0.4，对于手征负折射介质，要求χ＞n。

图2 ＜n+＜n1时的能流反射率和透射率Fig.2 The reflectivity and transmittance of energy current

当右旋正椭偏振电磁波入射时，由图2a可以看出：随着入射角增大到cθ−，折射波中的左旋圆偏振电磁波变成表面波，无法在介质中传播，透射率有所下降，同时，反射率增大；当入射角继续增大到cθ+时，折射波中的右旋圆偏振电磁波也变成表面波，此时，能量被全部反射，即发生了全反射，能流反射率变为1，透射率变为0。

左旋正椭圆偏振电磁波入射，能流反射率和透过率随入射角的变化如图2b所示。当入射角增大到cθ−，透射率明显下降；入射角变为cθ+时，发生全反射，反射率为1，透射率变为零。

在入射角变化的整个过程中，能流的反射率与透射率之和始终为1，遵循能量守恒定律。

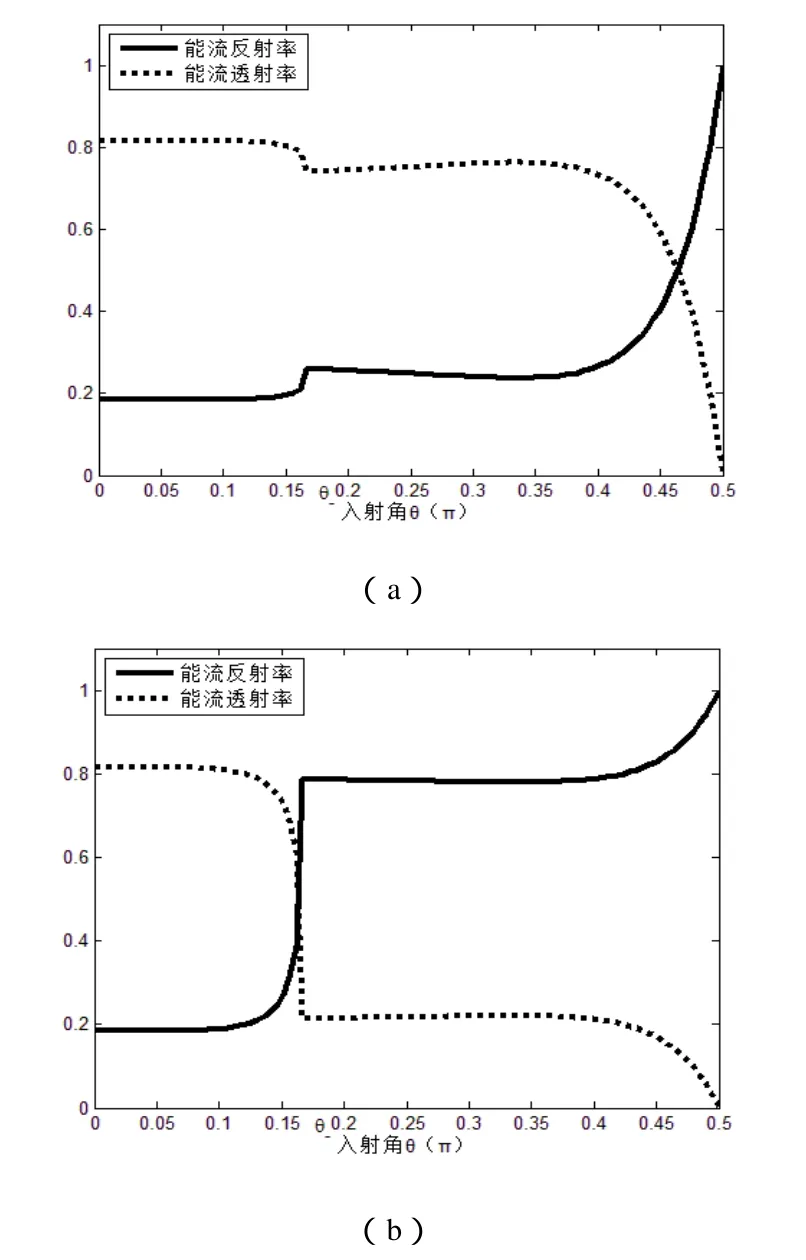
图3 ＜n 1＜ n +时的能流反射率和透射率Fig.3 The reflectivity and transmittance of energy current

右旋椭圆偏振波入射时，能流反射率和透射率随入射角的变化得曲线比较平缓。当入射角增大到临界角cθ−，能流反射率和透射率有一个比较小的跃变，由于左旋圆偏振波变成表面波，因此能流反射率增大，能流透射率减小。此后，能流反射率和透射率没有跃变，也无全反射现象。且在整个过程中，流反射率和透射率和恒为1，即满足能量守恒定律。

左旋椭圆偏振电磁波入射的情况与右旋椭圆偏振波入射类似，能流反射率和折射率只是在θc−处的跃变较大。

（3）取χ=1.5，n1＜＜ n+，此时，不论是右旋圆偏振电磁波还是左旋圆偏振电磁波，都不存在临界角。平均能流反射率和透射率随入射角的变化如图4所示。

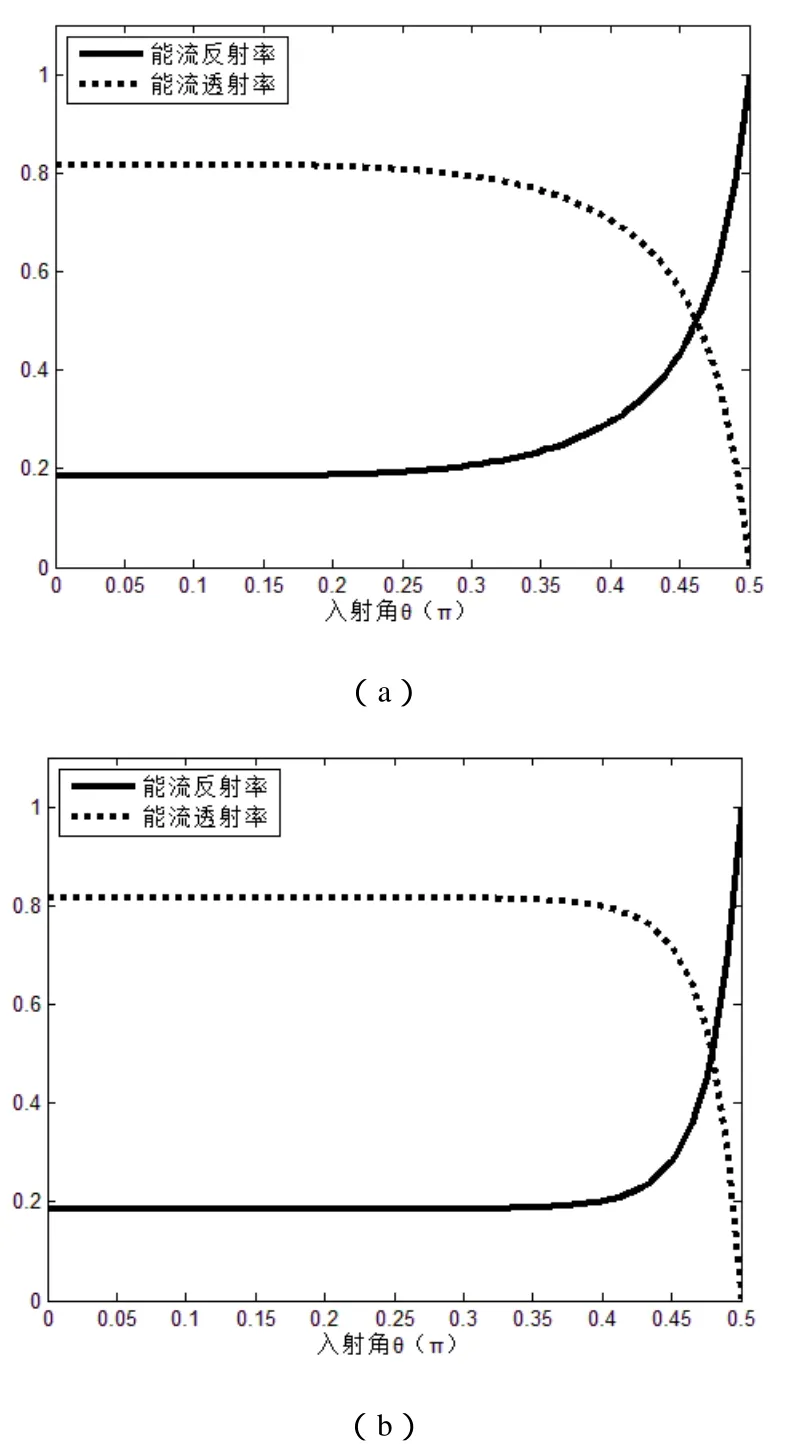
图4n 1＜ ＜n +时的能流反射率和透射率Fig.4 The reflectivity and transmittance of energy current

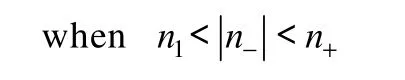
由图可以看出，不论对于右旋椭圆偏振电磁波入射还是左旋椭圆偏振电磁波入射，能流的反射率和透射率在整个入射角变化范围内都不存在跃变，它们随入射角的变化是一条平滑的曲线，没有全反射现象的发生。且整个过程中能流的反射率和透射率和为1，满足能量守恒定律。

5 结论

由于手征负折射介质中电磁波的传播现象与经典理论不同，无法用已有的理论公式进行讨论。本文依据手征负折射介质的本构关系，讨论了椭圆偏振电磁波在手征负折射率介质与常规介质表面的反射与折射特性，并给出了能流反射率透射率随入射角变化的曲线。结果显示，在手征介质存在两个本征波，它们有着不同的传播特性：

（1）当手征参数大于介质折射率时，本征波中的左旋圆偏振电磁波会发生负折射，这种介质被称为手征负折射介质。

（2）在手征参数取不同值时，对应两个本征波存在两个、一个或者不存在临界角；当两个本征波都存在临界角时，会出现全反射现象，其他两种情况不会发生全反射。

（3）不同偏振态的椭圆偏振电磁波入射时手征负折射率介质表面时，会产生不同的反射和折射现象。

[1] 吕启东,杨丽君.左手材料理论及研究进展[J].保定学院学报,2010,23(3):38-43.

Lü Dongqi,Yang Lijun.Advance in research and theories of left-handed materials[J].Journal of Baoding University,2010,23(3):38-43.

[2] 董建峰,徐超,徐键.手征负折射研究进展[J].量子电子学报,2009,26(4):386-393.

Dong Jianfeng,Xu Chao,Xu Jian.Research progress in chiral negative refraction[J].Chinese Journal of Quantum Electronics,2009,26(4):386-393.

[3] 董建峰,陶卫东.平行手征光纤之间的耦合系数[J].量子电子学报,2000,17(1):11-16.

Dong Jianfeng,Tao Weidong.Coupling coefficient between parallel chiral optical fibers[J].Chinese Journal of Quantum Electronics,2000,17(1):11-16.

[4] 董建峰,柳斌.手征负折射平行板波导中模式的新特性[J].电波科学学报,2008,23(4):597-600.

Dong Jianfeng,Liu Bin.Novel characteristics of modes in chiral negative refraction parallel-plate waveguide[J].Chinese Journal of Radio Science,2008,23(4):597-600.

[5] 柳斌,董建峰.圆偏振光在手征负折射材料表面的反射和极化特性研究[J].量子电子学报,2008,25(4):397-401.

Liu Bin,Dong Jianfeng.Reflection and polarization characteristics of circularly polarized light at the surface of a chiral negative refraction medium[J].Chinese Journal of Quantum Electronics,2008,25(4):397-401.

[6] 游开明,文双春.电磁波在正负折射率介质分界面上的折射与反射[J].衡阳师范学院学报,2004,25(6):18-21.

You Kaiming,Wen Shuangchun.Reflection and refraction of electromagnetic waves at the interface between media with positive and negative refractive indices[J].Journal of Hengyang Normal University,2004,25(6):18-21.

[7] 韩承江,柳斌,杨亦红.线偏振光在手征负折射材料表面的传输特性研究[J].量子光学学报,2010,16(2):140-144.

Han Chengjiang,Liu Bin,Yang Yihong.Research on the propagation characteristics of linearly polarized light on the surface of a chiral negative refraction medium[J].Acta Sinica Quantum Optica,2010,16(2):140-144.

[8] 郭硕鸿.电动力学[M].第三版.北京:高等教育出版社.2008:117-121.

[9] 郑植仁.光学[M].哈尔滨:哈尔滨工业大学出版社.2007:67-72.

[10] 蒋练军,金辉霞.椭圆偏振电磁波的反射和折射[J].大学物理,2006,25(1):38-40.

Jiang Lianjun,Jin huixia.Reflection and refraction of an elliptical polarized electromagnetic wave[J].College Physics,2006,25(1):38-40.

[11] 冯宇,吴健,宋建平.负折射指数物质[J].武汉大学学报,2005,51(S2):57-59.

Feng Yu,Wu Jian,Song Jianping.negative refractive index material[J].Journal of Wuhan University:Natural Science Edition,2005,51(S2):57-59.