多冷源空调系统节能优化调度算法初探

陈众励 许维胜

（同济大学 上海 201804）

1 引言

城市综合体建筑规模庞大（单体建筑面积可达数十万乃至百万平方米，建筑高度可达数百米），内部功能复杂（通常包括商业、餐饮、影视、宾馆和办公等不同业态），建筑能耗巨大，其中采暖与空调系统能耗约占一半，故节能潜力相当可观。

为满足城市综合体建筑中各种不同业态的空调需求，通常设置多种冷源系统（或装置）。常见的冷源系统（装置）包括：

（1）冷水机组，由电力驱动空气压缩机使冷媒降温；

（2）溴化锂机组，由天然气、人工煤气等燃气燃烧产生的热量使冷媒汽化，并间接制冷；

（3）热电冷三联供系统，以燃油发电机驱动发电机组产生电能，同时将发电机的余热用于冷媒的汽化并间接制冷；

（4）冰蓄冷装置，在公共电网用电低谷时段（同时也是电价的低谷时段）用电力驱动冷冻机组进行制冰作业，并在此日通过融冰达到制冷目的；

（5）地源热泵系统，利用深层地表的恒温特性（12 ℃左右），将部分空调系统的冷水管网深埋地下，使其与地表土壤进行热交换，从而对室内空气进行冷却。

（6）自然风空调系统，当室外温度显著低于室内温度时，利用室外冷却塔将空调系统的冷水进行自然冷却，从而达到令室内降温的目的。

上述各种制冷装置所消耗的能源种类不尽相同，制冷效率不同，制冷成本也不同。通过对这些不同种类的冷源、在不同电价区间（取决于一天内的不同时间段）内的优化调度，达到综合能耗最低或运行成本最低，是多冷源空调系统节能优化调度算法的核心研究目标。

2 城市综合体建筑多冷源空调系统节能优化调度问题的描述

2.1 系统调度的目标

城市综合体建筑多冷源空调系统需要在确保室内环境舒适性的前提下，同时实现下列目标：

（1）耗电最少。

（2）基于峰谷电价制度的电费最少，其中，任意一天内的的电价P（t）为阶跃函数。

（3）耗燃气最少。

（4）燃气费用最少，设定任意一天内的燃气价格为常数。

（5）耗柴油最少。

（6）柴油费用最少，设定任意一天内的柴油价格为常数。

为了电费最少，就应减少电价高峰时段（午后和初夜）的耗电，在夜间电价低谷时段（子夜和凌晨）应合理的多用电能制冰蓄冷。而这一目标（电费最少）与耗电最少的目标并不完全一致。

为了实现单纯的耗电最少的目标，就应尽可能地不用或少用耗电的冷水机组、冰蓄冷系统（该系统利用夜间低电价时段进行制冰蓄冷，故需消耗大量电能，虽然省钱但不节能）、地源热泵系统（该系统工作时需开启循环水泵等用电设备）以及自然风空调系统（该系统工作时需要运行冷却塔风机、水泵等耗电设备），同时用足或多用以天然气为主要能源的溴化锂空调系统和以柴油为主要能源的热、电、冷三联供系统。

为了实现单纯的耗天然气最少的目标，显然就应尽可能地不用或少用溴化锂机组，同时用足或多用耗电的冷水机组、冰蓄冷系统、自然风空调系统，以及耗油的三联供系统。

类似地，为了实现单纯的耗柴油最少的目标，则应尽可能地不用或少用耗油的三联供系统，同时用足或多用耗电和耗天然气的空调设备。

由此可见，目标1）和目标2）的最优值是不同步的（即存在利益冲突）；目标 3）与目标 4)的最优值是同步的（即利益一致）；目标5）和目标6）的最优值是同步的；目标1）、目标3）、目标5）的最优值之间互不同步；目标2）、目标4）、目标6）之间的最优值互不同步。

因此，城市综合体建筑多冷源空调系统的节能优化调度问题是一组相互排斥的目标集。

2.2 系统调度问题的约束条件

为了满足城市综合体建筑室内环境的舒适性要求，多冷源空调系统的节能优化调度问题应同时满足下列约束条件：

（1）各子系统的制冷量之和应等于建筑物所需总冷量C（t），其中C（t）为时变函数。

（2）冷水机组的制冷量不大于其额定值，即，C1（t）≤C1（常数）;

（3）溴化锂机组的制冷量不大于其额定值，即，C2（t）≤C2（常数）；

（4）三联供系统的制冷量不大于其额定值，即，C3（t）≤C3（常数）；

（5）冰蓄冷系统的制冷量不大于其额定值，即，C4（t）≤C4（常数）；

（6）地源热泵系统的制冷量不大于其额定值，C5（t）≤C5（常数）

（7）自然风系统的制冷量不大于其额定值，即，C6（t）≤C6（常数，设计最大值）。

上述约束条件构成了多冷源空调系统的约束集。

综上所述，城市综合体建筑多冷源空调系统的节能优化调度问题中，需要满足约束条件的前提下，同时处理多个相互矛盾、相互排斥的目标，故可以归结为约束型的多目标优化调度问题（Multiobjective Optimization Problem，MOP，也称MOPSO）。

3 多目标优化问题的基本算法

3.1 多目标优化问题的一般描述

多目标优化问题一般由 n个决策变量、k个目标函数和m个约束条件组成，且三者之间存在某种函数关系。[1-2]

一般多目标优化问题的数学描述如下：[3]

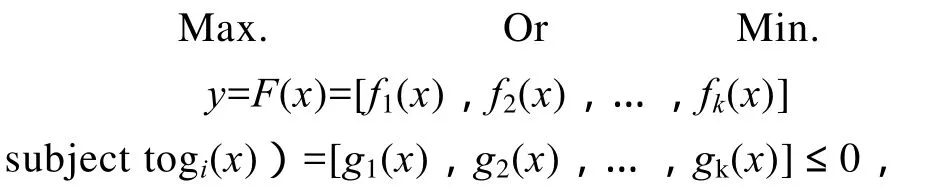
X表示决策向量组成的集合，称为决策空间（decision space）或参数空间（parameter space）。决策向量（decision vector）x=（x1，x2，…，xn）由n个决策变量组成。

Y表示目标向量形成的目标空间（objective space）或判据空间（criteria space）。

目标函数F（x）将决策向量x映射成一个k维向量y=（y1，y2，…，yk），该k维向量称为目标向量（objective vector）或判据向量（criteria vector），记作F：Ω→∧。

约束条件gi（x）≤0决定决策向量可行的取值范围。

由于目标函数和约束条件可能是线性或非线性、凸或凹或不凸不凹、可微或不可微、连续或不连续、单峰或多峰的，因此目标空间和决策空间可能是凸或非凸、紧或非紧、连通或分离的[4]。显然，问题的规模由决策变量、约束条件和目标数量共同决定，在MOPOS优化过程中，各个目标往往是相互冲突的，达到各自极值的时机无法同步，因此并不存在一个在约束条件内能使所有目标函数达到全局最优的解。为此，必须首先找出最优解（Pareto Dominance，也称非劣最优解）的可行解集和最优解前端，并最终搜寻出最优解。

3.2 非劣最优解的评价方法

对多目标问题最优解的评价方法实质上是一种建立在集合论基础上的优劣性评价体系。所谓非劣最优解是指在目标函数的解集中，对其中一个或多个子目标函数的进一步优化不会使其它子目标函数的解失效（即超出规定的范围），也即在多目标优化中对某些子目标的优化不会影响到其它子目标的优化而容许的整个多目标体系的解。

为建立解的优劣性评价体系，在最优解中引入了支配向量（Dominate Vector）的概念，其定义为：

基于对支配关系的判断，并可筛选出非劣最优解（Pareto Dominance）、全局最优解（Globally Optimal Solution）和Pareto最优解集：

（1）若x*是搜索空间（决策变量）中的一点，当且仅当在搜索空间的可行域内不存在x使得fn(x)≤fn(x*)(n =1 ,2,… ,N)成立时，称 f(x*)为非劣最优解。

（2）对于多目标优化问题的f(x)，当且仅当在搜索空间中的任意x，f(x*)≤f(x)都成立时，则称 f(x*)为全局最优解。

（3）由所有非优劣最优解组成的集合即为多目标优化的Pareto最优解集。

Pareto最优解集对应的所有目标函数值所形成的空间便是所谓的Pareto前端（Leading End）。

解决了解的评价问题后，面对各种不同的多目标问题算法，建立对算法性能的评价体系显然是有意义的。

3.3 多目标优化算法的性能评价

多目标优化算法的评级体系主要包括下列指标：

（1）逼近性（Generational Distance，GD），反映了算法所获得的非劣最优解与Pareto前端的距离。其定义为

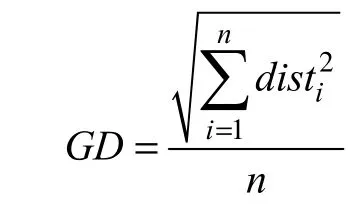
式中disti表示第i个非劣解与Pareto前端的距离。

（2）均匀性（Spacing，SP），反映了非劣解在Pareto前端上的分布范围，其定义为：

式中，di是两非劣解间的距离，是其平均值。

（3）宽广性（Extention，EX），反映了非劣最优解的分布范围。

（4）最优解差错率（Error Ratio，ER）用来描述在算法获得的非劣最优解中不属于Pareto前端的解所占的比例。

（5）收敛性度量值γ，用来衡量一组已知的Pareto最优解集的收敛范围。

收敛性度量的评价方法为在多目标优化问题的Pareto前端均匀地取若干点构成Pareto前端基点系，计算由算法获得的Pareto最优解与基点之间的距离的最小值，所有这些最小值的平均值就是收敛性度量值γ。

（6）多样性度量值Δ，用来衡量Pareto前端的分布均匀度，其定义为：

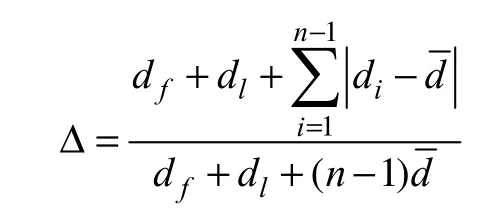
式中，di是两非劣解间的距离，是其平均值，df是Pareto前端中极值点的距离，dl是边界点的距离。

其中，非劣解的收敛性和多样性对 MOP算法评价的核心指标。[5]

4 基于粒子群优化算法（PSO）求解多目标问题的基本思路

在Reynolds提出的BOID鸟群模型[6]中，每只鸟类个体的行为只和它相邻个体的行为有关，并遵循“避免碰撞（Collision Avoidance）、速度一致（Velocity Matching）和趋向中心（Flock Centering）”的基本原则。在初始状态下，鸟群中的个体在随机位置上往随机方向自主飞行，但在“避免碰撞、速度一致和趋向中心”三原则的驱使下，最终所有个体通过自组织（Self-organization）趋于一致并汇聚于食物所在位置。

受上述 BOID鸟群模型的启发，Kennedy和Eberhart共同提出了粒子群优化算法（PSO）[7]。在这一算法模型中，每个粒子的自身状态都由位置向量和速度向量来描述，这两个参数分别代表问题的可行解和它（粒子）在搜索空间中的运动方向。粒子通过迭代搜索，不断学习它当前的群体最优解和个体最优解，最终达到全局最优。粒子的位置和速度的迭代方程是PSO算法的核心，在连续空间中其基本算法（适用于单个目标的情形）描述如下：

设在一个N维的目标搜索空间中，有M个粒子组成一个群落，将第i个粒子表示为一个N维的向量：

pin=（pi1，pi2，…，piN），其中，i=1，2，…，M。

即第i个粒子在N维搜索空间中的位置是pin。每一个粒子都是潜在的解，将pin代入一个目标函数就可以计算出其适应值，根据适应值的大小衡量pin的优劣。第i个粒子的飞行速度也是一个N维的向量，记为vin=（vi1，vi2，…，viN），速度决定粒子在搜索空间单位迭代次数的位移。

记第 i个粒子群当前搜索到的最优位置为：ppbestn=（ppbest1，ppbest2，…，ppbestN）,整个粒子群当前搜索到的最优位置为pgbestn=（pgbest1，pgbest2，…，pgbestN），粒子按照下列公式来迭代更新其速度和位置:

其中，i=1，2，...M；

n=1，2，...N；

ω为权重惯量，其主要作用是避免早熟而陷于局部最优。比较简单的处理方式是将其初始取值为0.9，然后在迭代过程中线性地递减到 0.4。也有文献建议按函数关系ω=ωmax−（ωmax−ωmin）IC/ICmax进行迭代计算（Iterative Computations），式中，ICmax为预定的最大迭代次数；

c1，c2为加速系数（Acceleration Coefficients，也称学习因子），c1=0，则忽略了个体经验，c2=0则忽略了群体经验，通常两者均不可取。一些文献建议在0～4之间的取值，而种群规模适中的工程应用中一般取2.0；

r1，和r2为介于[0，1]之间的随机数；

V（i+1）n∈[−vmax，vmax]，vmax为常数（可根据经验设定），vmax的每一维通常取相应维的取值范围的10%～20%[7]。

上述计算公式中，等式右边的第一部分为惯性分量，是遗传（或继承）粒子上一次运动结果的矢量；第二部分为个体认知量，是反映向个体历史最优位置运动的量；第三部分为群体认知量，是反映粒子向全局最优位置运动的量。

迭代中止条件可选为粒子群搜索到的最优化位置满足适应阈值或达到预定的最大迭代次数。由于pgbestn是整个粒子群的最优值，因此上述 PSO算法也称为全局PSO算法。全局 PSO算法收敛速度较快，但有可能陷入局部最优。

如果把第 i个粒子的邻居粒子搜索到的最优位置作为pgbestn，则上述方法可称为局部 PSO算法。与全局PSO算法相比，该收敛速度较慢，但相对而言不易陷入局部最优。

PSO基本算法的流程图[8]如下：

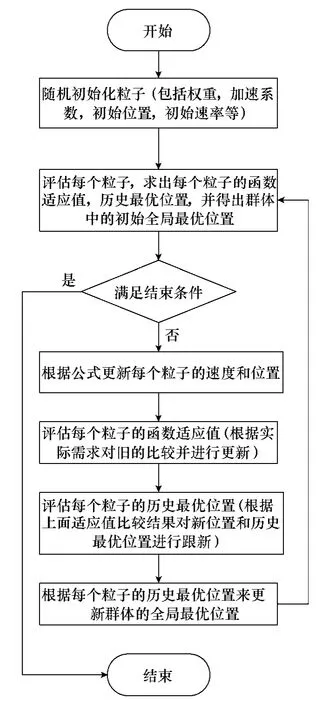
流程图中单目标 PSO算法的基本思路可以描述为：

→初始化粒子位置（一般都是随机生成均匀分布）

→计算适应度值（一般是目标函数值-优化的对象）

→初始化历史最优 ppbestn为其本身和找出全局最优Pgbestn

→根据速度和位置公式分别进行速度和位置的更新

→重新计算适应度

→根据适应度更新历史最优 Ppbestn和全局最优Pgbestn

→收敛或者达到最大迭代次数则结束运算

其中，在解决实际工程问题时，种群规模、权重惯量、加速系数等参数需要在对工艺条件进行深入研究的基础上才能合理地确定。对于城市综合体建筑多冷源空调系统而言，系统所需的总冷量具有时变、随机和离散（各个空调冷源系统的输出可能是连续变量，也可能是离散变量，取决于控制方式。）等特性，而且多冷源空调系统也诸多客观条件的限制（约束条件）。

在PSO算法中引入群体智能（Swarm Intelligence SI）的思想[9-10]，将使算法具有收敛快、精度高且容易实现等优点，这对于解决诸如多冷源空调系统节能优化调度之类组合优化问题颇具优越性。

5 约束型多目标调度问题的智能微粒群优化算法及其改进

用 PSO的基本算法来解决多目标优化问题将面对两个困难。

首先需要解决Ppbest的选择问题。对于单目标优化问题而言，选择Ppbest时，只需作简单比较就可以选择出哪个是当前最优。但是对于多目标问题而言，两个粒子之间的简单对比，并不能判断出哪个更优。因为很可能某个粒子比一部分粒子好，但又比另一部分粒子差，或者说不存在绝对好的粒子。

其次需要解决Pgbest的选择问题。对于单目标问题而言，在种群中只有一个最优的个体（Pgbest）。而对于多目标问题而言，最优的个体可能有多个（Pgbest族）。但是PSO基本算法的规则体系中，只允许选择一个粒子作为最优的个体（引领者）。

对于第一个问题，通过仔细分析PSO算法的机理，我们就能发现其实比较容易处理：虽然我们不能通过简单比较筛选出历史最优，但可以随机选择其中一个作为历史最优，让运算规则来找到实际最优。

对于第二个问题，Carlos A等人于2004年提出了在最优集（存档，Archive）中根据拥挤程度选择引领者的策略，其主要规则是尽量选择处于不拥挤位置的粒子，比如使用网格法（Grid）[11]进行选择。

MOPSO算法在选择引领者和对存档（Pareto当时最优集）进行更新时，可以应用自适应网格法，其基本策略为：[12]

根据网格划分，假设每个网格中粒子数为g个，i代表第几个网格。该网格中的粒子被选择的概率为pi=1/gi，即粒子越拥挤，则选择的概率越低。这是为了确保那些未知区域也能得到探索。

在种群更新完成之后，存档工作通过三轮筛选来完成：

→根据支配关系进行第一轮筛选，将劣解去除，剩下的加入到存档中；

→在存档中根据支配关系进行第二轮筛选，将劣解去除，并计算存档粒子在网格中的位置；

→若存档数量超过了存档阀值，则根据自适应网格进行筛选，直至达到阀值限额为止。然后，重新进行网格划分。

显然，改进后的智能微粒群优化算法更适用于解决多目标优化问题。

6 约束型多目标优化调度算法的工程化过程中应注意的问题

基于智能微粒群优化算法的约束型多目标问题求解过程具有较好的收敛性，故具有较好的应用前景。但应注意的是，多冷源空调系统的运行条件具有明显的动态特性。因为大型建筑中，空调系统总制冷量C值受诸多因素影响，其因素包括：

（1）室外热辐射F（t），具有随机性，但可通过检测设备获得实时数据并输入调度系统中。

（2）室内人数P（t），具有随机性，但可通过检测设备获得实时数据并输入调度系统中；建筑物内人员的作息表，可预订规则并输入调度系统中。

（3）建筑照明系统的空调负荷经由智能控制系统的调节而呈现出动态。

（4）配电系统中，电力变压器的热损耗约占其自身功率的2%，并随着其负载率的变化而变化。

因此，建筑物的总制冷量为时变函数，且具有明显的随机、离散分布特性，这些因素都是工程化过程中需要重点研究和解决的问题。

7 结论

本文从大型建筑物中多冷源空调系统的节能优化调度问题出发，探讨了以智能粒子群算法为基础的约束型多目标优化问题的算法及其改进方向。此类算法只有在经历仿真实验、现场试运行及最终定型等工程化蜕变过程后才有可能在实际工程中得到广泛应用。

[1] Van Veldhuizen DA.Multiobjective evolutionary algorithms:classifications,analyses,and new innovations(PHD thesis).Ohio:Air Force Institute of Technology,Wright-Patterson AFB,1999.

[2] 崔逊学.基于多目标优化的进化算法研究[D].安徽:中国科技大学,2001.

[3] 郭文忠,陈国龙.离散粒子群优化算法及其应用[M].北京:清华大学出版社,2012.

[4] 于堷杰,周根贵译.遗传算法与工程优化.北京:清华大学出版社,2003.76-108.

[5] 章勇高,高彦丽,刘焕等.三相不平衡时的PWM整流器锁相环设计[J].华东交通大学学报.2011,28(5):14-17.

[6] 肖晓伟,肖迪,林锦国.多目标优化问题的研究概述[J].计算机应用研究,2011,28(3):805-808.

[7] Kennedy J,EberhartRC.Partcls swarm optimization.[C].Proceedings of IEEE international Conference on Neural Networks.Piscataway,NJ:IEEE Service Center,1995.1942-1948.

[8] 张军,詹志辉,等,计算智能[M].北京：清华大学出版社,2009.

[9] 吴启迪,汪镭.智能微粒群算法研究及其应用[M].南京：江苏教育出版社,2005.

[10] 高尚,杨静宇.群智能算法及其应用[M].北京：中国水利水电出版社,2006.

[11] Carlos A.Coello,GregorioToscanoPulido,Maximino Salazar Lechuga.Handling multiple objectives with particle swarm optimization[J].IEEE Transactions on Evolutionary Compution,2004,8(3):

[12] Joshua D.Knowles,Approximating the non dominated front using the Pareto Archived Evolution strategy,UK,Evolutionary Computation,8(2),149-172,2000.