磁性液体微压差传感器动态建模研究

刘雪莉 杨庆新 杨文荣

（1.河北工业大学电磁场与电器可靠性省部共建重点实验室 天津 300387；2.天津工业大学电工电能新技术天津市重点实验室 天津 300387）

1 引言

磁性液体是一种将纳米级铁磁材料颗粒利用表面活性剂均匀、稳定地分散在某种液态载体之中，所形成的稳定胶体悬浮液[1]。由于其兼具良好的流动性和超顺磁性，被广泛应用在密封、航天、传感测量、生物医学和环保等领域[2-4]。近年来，基于磁性液体的各类传感器不断涌现[5-11]，传感器的动态特性却较少提及[12]。而传感器的动态性能是传感器特性的重要指标之一，因此对磁性液体传感器的动态特性进行分析建模，有利于此类传感器的进一步发展。

由于磁性液体的传感器多数涉及磁场、流体场共同作用的环境，会出现磁—机耦合、流—固耦合、气—液耦合等情况，因此，传感器的动态性能会受到较多因素的影响，且磁性液体的粘度在磁场中的变化也是重要的影响因素。现有研究有基于能量守恒定律对微压差传感器动态特性进行分析的[13]，但未考虑磁性液体的磁粘特性。

本文分析了课题组设计的磁性液体微压差传感器的基本结构，阐述了其工作原理；而后对传感器内部的磁场和流体场进行分析，考虑了粘度在磁场中的变化，根据流体运动学理论，建立了分步耦合与强耦合模型，以表征传感器的动态特性；最后对该模型进行了仿真，结果与理论推导值具有一致性。

2 微压差传感器的基本原理

本文设计的磁性液体微压差传感器结构模型如图1所示，U形玻璃管中装有磁性液体，初始液面位于线圈的中部，每个管臂外有两组完全对称的线圈，其中激励线圈1和3，作为产生磁场的激励源；感应线圈2和4，用于测量感应电压u2和u4。

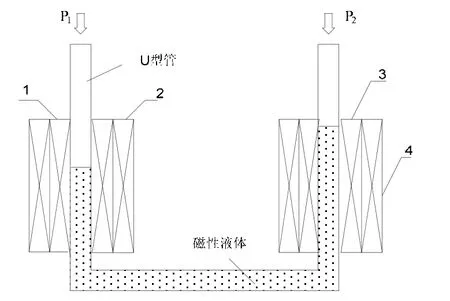
图1 磁性液体微压差传感器模型图Fig.1 Model for the differential pressure sensor

线圈1和3正向串接，线圈2和4反向串接。其等效电路如图2所示，i为激励源，Li（i=1，2，3，4）为4个绕组的电感值，Ri（i=1，2，3，4）为4个绕组的电阻值。

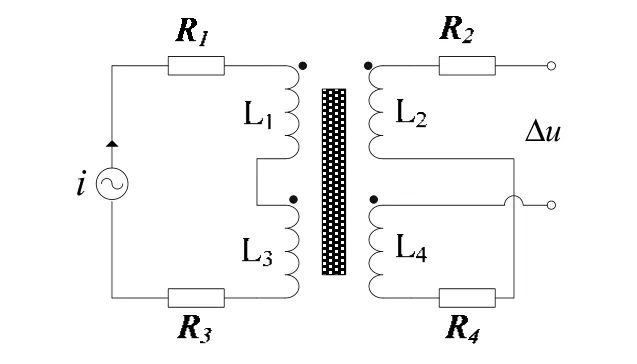
图2 微压差传感器的等效电路Fig.2 Equivalent circuit of pressure sensor

激励绕组加正弦电流 i，该电流产生一个交变磁场。当U形管两端压力差ΔP=P1−P2≠0时，试管两侧因为磁性液体的液面高度不同而磁场分布不同，则两线圈产生感应电压差Δu=u2−u4≠0。ΔP越大，液面高度差越大，则Δu越大。

激励线圈施加正弦电流i

激励线圈的电压为

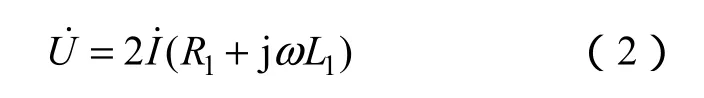
式中，R1、L1分别为激励线圈的等效电阻和电感。

U形管左右两侧的感应电压有效值为

式中，Ma和Mb分别为U形管左右两侧的激励线圈对感应线圈的互感系数。则U形管左右两侧的感应电压差有效值为

无压力差时U形管两端的液面高度相等，存在压差Δp时，磁性液体由高压端向低压端流动，产生液面高度差为Δl，忽略管臂线圈内的磁场梯度，即认为磁场是均匀的，忽略磁性液体所受磁场力和粘性力，则有

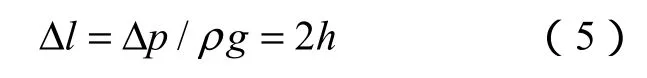
式中，h为磁性液体单侧管臂中移动的距离；ρ为磁性液体密度；g为重力加速度。

由于磁性液体的流动，两侧线圈的互感 Ma和Mb不再相等，使输出电压差ΔU发生变化。

3 微压差传感器耦合模型

3.1 分步耦合模型

磁性液体微压差传感器中的磁场主要由U形管两臂上的线圈提供，激励线圈通入的是正弦交流电，故管内部的交变电磁场是交流正弦变化的电磁场。忽略位移电流，麦克斯韦方程组微分形式可以表示为[14]：

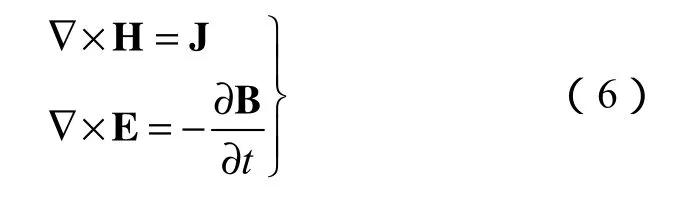
式中，B为磁感应强度，H为磁场强度，J为传导电流。

磁性液体是对周围电磁场能够做出响应，并且和电磁场相互影响的流体，在没有外加磁场时没有磁性，在外加磁场下，表现为超顺磁性。磁性液体在外磁场中受到的磁场力来源于其中的固相磁性颗粒，在外磁场作用下，各个固相微粒都发生不同程度的磁化。每个磁化分子都在其周围形成磁场。取磁性液体中的一个微元控制体作为分析单元，该微元体内必包含大量固相微粒，按分子电流观点[15]，每个固相颗粒可用一个分子电流环来替代，其磁化强度M =B'/μ0可用环形电流表示，全部微粒的磁化强度的矢量和就是整个微元体的磁化强度。

磁性液体内总的磁感应强度B可表示为

式中，B0是外磁场的磁感应强度，B'是物质磁化产生的附加磁感应强度，μ0是真空磁导率，M是磁化强度矢量。

定义矢量磁位A，满足

根据矢量场旋度的概念可得

根据磁性液体的磁化强度曲线，若传感器激励线圈内的磁场小于 200Gs，磁性液体工作在线性区域，则有

式中，χm为磁性液体的磁化率。

微压差传感器模型中存在磁场—流体场—热场等多场的耦合作用，考虑磁性液体流动所带来的温升较小，可忽略温度的影响，简化建立磁场—机械场（流体场）的有限元模型，其相互耦合关系如图3所示。

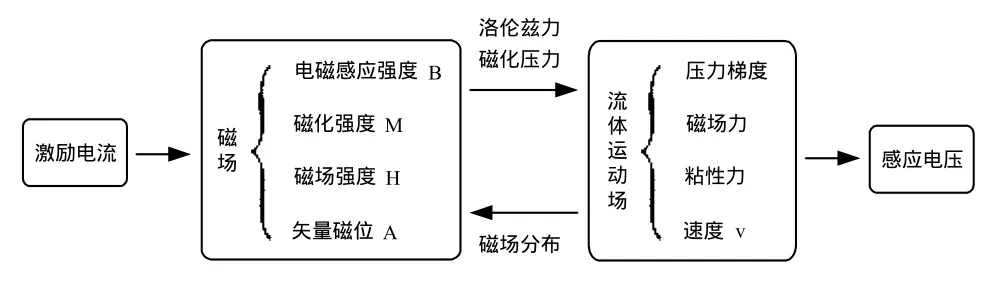
图3 分步耦合关系图Fig.3 Step by step coupling relationship

用不可压缩粘性流体的运动微分方程表示磁性液体在U形管中的运动，为

式中fmx，fmy，fmz为磁性液体x，y，z三个方向所受的磁场力，vx、vy、vz分别为磁性液体沿x，y，z方向的速度，η为磁性液体的粘度。

单位体积的磁性液体在流体场中所受的磁场体积力为F，即[16]

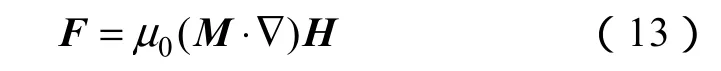
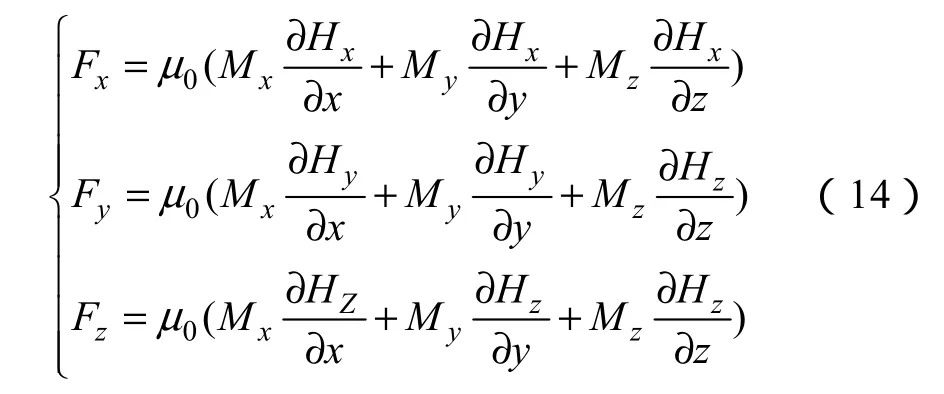
联立式(12)、(14)可得，磁性液体在磁场中的运动方程

Γ1和Γ2是微压差传感器内部磁性液体的力学边界条件和磁学边界条件：

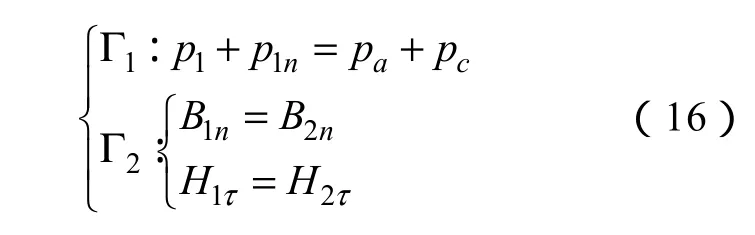
式中pa为大气压力，pc为磁性液体的表面张力，下标“1”表示磁性液体边界的内侧，下标“2”表示磁性液体边界的外侧。

微压差传感器内部磁性液体的初始条件：液体速度场为零，外部激励磁场恒定。

由式（15）可知，磁场对磁性液体产生的体积力和外界压力影响流体场中磁性液体的流速，流速的变化会影响到U形管两侧液面差的产生，即磁性液体微压差传感器磁芯位置发生改变，进而影响到磁场的分布，这就是传感器的磁-机械耦合效应。

假定磁性液体处于静止状态，计算磁场分布，由此磁场分布进行流体运动场的计算，根据新的运动场，假定液体静止，再次计算磁场，计算出的磁场再次进行运动场计算，直至误差满足条件停止迭代，由此时的磁场分布可求得U形管两臂的感应电压差，以此表征两侧压力差，图4即为分步耦合算法的迭代流程。

图4 分步式弱耦合算法的迭代流程图Fig.4 Iterative flow chart of step by step coupling algorithm

3.2 强耦合模型

上述分步耦合模型，磁场和流体运动场在计算时，均假设一种场是固定的，进行相互的迭代；但在实际中，微压差传感器内部的磁场和流体场每一个时刻均在变化，且磁性液体的粘度对流体的运动有很大影响，而粘度在磁场下是变化的，因此建立微压差传感器强耦合模型，将更符合实际的情况。

假定磁性液体为牛顿流体，基于经典流体动力学理论，单位体积磁性液体在磁场中运动方程的基本形式为：

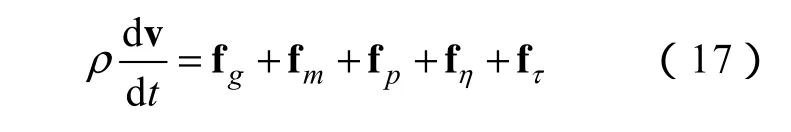
上式右边各项：

（1）fg为磁性液体的重力，是体积力，表示为

（2）fm是磁场力，即 Kelvin力，是磁性液体特有的由外磁场引起的一种体积力[16]，表示为

（3）fp是磁性液体受到的压力梯度，是一种表面力，表示为此处没有上提一行，麻烦请修改，非常感谢

此处的压力p仅指外界压力差ΔP，若从能量的角度考虑，还包括磁性液体在磁场中磁化产生的磁化压力 pm和在磁场中体积变化引起的磁致伸缩压力ps，可表示为

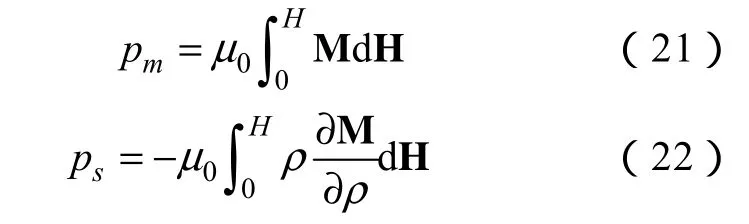
（4）fη是粘性力，表示为

实际中磁场对磁性液体粘度有影响，记为ηH。在微压差传感器的模型中，磁性液体的密度ρ为常数，即为不可压缩流体，即0=⋅∇v，则有

（5）fτ是磁性液体内部固相颗粒转动引起的附加力，即考虑磁性液体为两相流时，液固两相涡旋的速度滞后产生的，此时将磁性液体当做均匀相流体对待，该力可认为等于零。

同时磁性液体的磁化强度矢量 M和磁场 H平行，有：

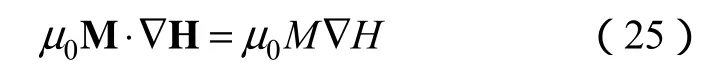
若不考虑磁性液体的磁致伸缩量，有：

磁场H的分布随着磁性液体的运动而改变，即ηH不为常数，为磁场H的函数，表示为：

综合式（17）～（27），则微压差传感器内磁性液体的动态耦合模型可表述为

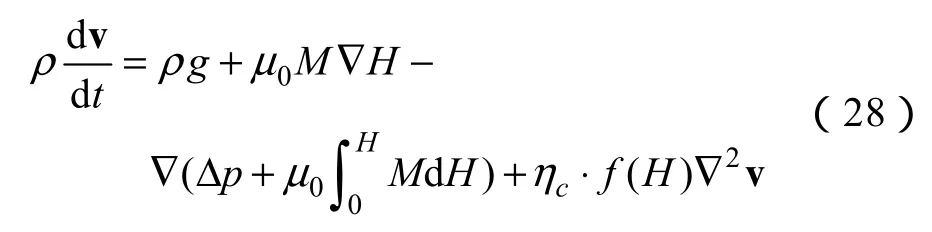
式(28)可看出，外磁场对磁性液体运动的影响表现在ηH上，通常外磁场改变磁性液体粘度对其运动的影响，比磁场力（即Kelvin力）的影响大得多。

4 磁性液体微压差传感器模型仿真

利用式（28）对微压差传感器进行仿真，模型如图5所示。

图5 传感器三维仿真模型Fig.5 The 3D simulation model of the differential pressure sensor

U形管内磁性液体的界面处于线圈的中间位置，当U形管两端压力差为恒定静压力，或频率较低的正弦压力源（10～50 Hz）时，管内磁性液体的流动为层流。

压差为恒定压力时，两感应线圈的感应电压差为幅值恒定的正弦波，频率与激励源相同。

压差为正弦压力时，图6为两侧液面高度水平集变量对管壁的积分，可看出，该传感器系统在初始压力为零的情况下开始加压，需要50ms左右的滞后过渡，在 0.1s之后，开始逐步跟随压力的变化，压力为正弦变化，液面的变化最终亦表现为正弦，且频率与压力源的频率一致。

图6 两侧液面高度Fig.6 The liquid height on both sides

当激励电源频率为1000Hz，压力源频率10Hz，两感应线圈的感应电压差稳定后的波形如图 7所示，呈幅值为正弦变化的正弦波，波形频率为激励源频率，幅值变化的频率为正弦压力源的频率，即波形的包络线为双正弦曲线。

图7 正弦压力差时感应电压差波形Fig.7 Induction voltage difference with sinusoidal pressure difference

图8中为感应电压差的上、下包络线，可看出与压差源波形一致。图9为仿真模型的输入输出曲线。

图8 正弦压力差时感应电压差波形包络线Fig.8 Induction voltage difference envelope with sinusoidal pressure difference

图9 微压差传感器输入输出曲线比较Fig.9 The input and output curves of the differential pressure sensor

分析结果可得：

(1)当外加压差相同时，不考虑粘度影响时得到的输出电压差值大于考虑粘度时的电压输出；

(2)当输出电压相同时，不考虑粘度影响时所对应的压差值要比考虑粘度时的小；

(3)考虑磁性液体的磁粘特性，相同压差下，输出电压值比考虑粘度为无磁场固定值时的输出更小，表明磁性液体在磁场下粘度增大，压力要克服的粘性力变大，位移变小，输出电压变小。

上述结论与理论分析是一致的。

5 结论

本文对一种磁性液体微压差传感器的基本工作原理进行了分析，并根据流体运动学理论，考虑了磁性液体粘度在磁场中的变化，建立了传感器磁场—流体场耦合模型。利用该模型进行了传感器动态特性的仿真，结果与理论推导值具有一致性。该模型为研究磁性液体微压差传感器的动态特性、优化传感器结构、提高传感器精度提供了理论依据和技术支持。寻找适合的正弦低频微压力源，对微压差传感器施压正弦压力，进行频域动态实验，将进一步验证动态模型的正确性。

[1] 池长青.铁磁流体的物理学基础和应用[M].北京:北京航空航天大学出版社,2011.

[2] 李德才.磁性液体理论及应用[M].北京:科学出版社,2003.

[3] Ilg P,Odenbach S.Ferrofluid structure and rheology[J].Lecture Notesin Physics.2009,763:249-325.

[4] Nowak J,Odenbach S.Magnetoviscous effect in a biocompatible ferrofluid[J].IEEE Transactions on Magnetics.2013,49(1):208-212.

[5] 郝瑞参.磁性液体微压差传感器的理论及实验研究[D].北京交通大学,2011.

[6] 郝瑞参,李德才.差动式磁性液体微压差传感器数学模型计算及试验验证[J].机械工程学报.2010,46(12):161-165.

Hao Ruican,Li Decai.Mathematic model and experiment of pressure difference sensor with magnetic fluid[J].Journal of Mechanical Engineering,2010,46(12):161-165.

[7] Jianhua Li,Rong Wang,Jingyuan Wang.Novel magnetic field sensor based on magnetic fluids infiltrated dual-core photonic crystal fibers[J].Optical Fiber Technology:Materials,Devices and Systems,2014,20(2):100-105.

[8] N.C.PoPa,A.Siblini,L.Jorat.Aspects concerning the dimensioning of the inductive transducers with magnetic fluids[J].Journal of Magnetism and Magnetic Materials,2002(242-245):1240-1242.

[9] B.Ando,A.Ascia,S.Baglio.A ferrofluidic inclinometer in the resonant configuration[J].IEEE Transactions on Instrumentation and Measurement,2010,59(3):558-564.

[10] G.Chitnis,B.Ziaie.A ferrofluid-based wireless pressure sensor[J].Journal of Micromechanics and Microengineering,2013,23(12):125031(6pp).

[11] B.Ando,S.Baglio,A.Beninato.A flow sensor exploiting magnetic fluids[J].Procedia Engineering,2011,25:559-562.

[12] W.Yang,Q.Yang,C.Fan，et al.Dynamic analysis and experiment on magnetic fluid acceleration sensor[J].International Journal of Applied Electromagnetics and Mechanics,2007,15(3):250-253.

[13] W.Yang,Q.Yang,W.Zhang.Dynamic response of pressure sensor with magnetic liquids[J].IEEE Transactions on Applied Superconductivity,2010,20:1860-1863.

[14] 颜威利,杨庆新,汪友华.电气工程电磁场数值分析[M].北京:机械工业出版社,2005.

[15] Rosensweig R E.Ferrohydrodynamics[M].Cambridge University Press,1985.

[16] 刘桂雄,蒲尧萍,徐晨.磁流体中Helmholtz和Kelvin力的界定[J].物理学报,2008,57(4):2500- 2502.

Liu Guixiong,Pu Yaoping,Xu Chen.Definition of helmholtz and kelvin forces in magnetic fluids[J].Acta Physica Sinica,2008,57(4):2500-2502.