一种特高压直流输电线路神经网络双端故障测距新方法

陈仕龙 谢佳伟 毕贵红 张 杰 张文英 高 超

（1. 昆明理工大学电力工程学院 昆明 650050 2. 南方电网科学研究院 广州 510080）

1 引言

特高压直流输电具有输送容量大、送电距离远、线路走廊窄等优点，因此在远距离电能传输方面具有明显的优势。我国幅员辽阔、能源与负荷呈逆向分布，决定了特高压直流输电技术在我国具有广阔的应用前景[1]。直流输电线路是直流系统故障率最高的元件[2]，由于直流输电线路一般较长，沿线地形复杂，环境恶劣，通过巡线的方式准确查找故障点变得异常困难，这严重影响了永久性故障的恢复时间。因此，研究准确、快速的直流输电线路故障测距技术具有较高的实用价值。

目前直流输电线路故障后的测距主要依赖于行波故障定位技术[3]，分为单端行波测距法和双端行波测距法。单端行波法需要准确识别第二个反射行波波头，高阻接地故障时第二个反射行波波头的正确识别存在困难；双端行波测距法能够准确定位的关键在于正确识别和标定故障行波首波头，由于直流输电系统中由平波电抗器和直流滤波器组成的线路边界对行波的高频及低频成分呈现不同的频率特性，这给故障行波首波头的正确识别和到达时间的准确标定带来了困难[4]。

直流输电线路发生故障时，故障点产生的故障高频信号将沿线路向两端传播，故障高频信号在线路上传播过程中将发生衰减[5-8]，据此文献[9]提出基于高频量衰减特性的特高压直流输电线路双端测距原理，该原理的测距精度依赖于线路衰减常数准确估算。高压直流输电线路因为沿线地形环境复杂，准确测量线路的参数存在困难，因而求取线路衰减常数有一定的困难。鉴于人工神经网络有很强的非线性逼近拟合能力，利用人工神经网络方法，将不必准确计算线路衰减常数也能准确实现故障定位。本文选取不同频带内整流侧和逆变侧测距装置处检测到的故障电压行波线模分量高频部分首波头幅值比作为 BP神经网络的输入样本集，故障距离作为输出样本集，对神经网络进行训练、测试，形成直流输电线路故障测距神经网络模型。不同过渡电阻下不同故障距离的大量仿真结果表明：该基于高频量衰减特性的特高压直流输电线路神经网络双端故障测距方法精度较高，而且耐受过渡电阻能力强。

2 基于高频量衰减特性的特高压直流输电线路双端测距原理

目前，特高压直流输电线路多采用双极模式运行，两极之间存在耦合，因此，在对线路上的电压信号进行衰减特性分析之前要先进行解耦运算。利用式（1）进行解耦得到独立的暂态电压模量分量[10]。

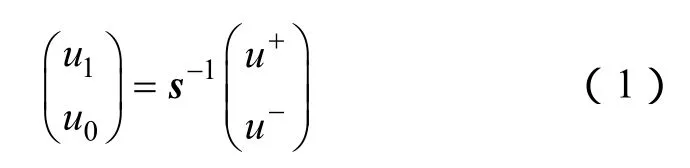
其中

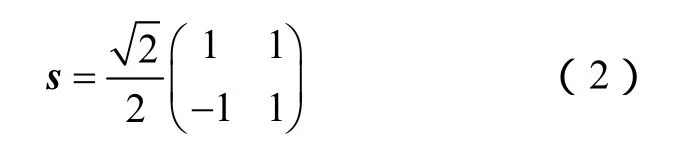
式中，u1、u0分别表示整流侧或逆变侧的暂态电压线模分量、零模分量；u+、u-分别表示该侧的正极线暂态电压、负极线暂态电压。

特高压直流输电线路对高频量有衰减作用，高频量的衰减程度与其通过的直流输电线路长度有密切关系。基于高频量衰减特性的特高压直流输电线路双端测距原理如图1所示。

图1 基于高频量衰减特性的特高压直流输电线路双端故障测距原理Fig.1 The double-ended fault location method of UHVDC transmission line based on high frequency component attenuation characteristic

根据文献[9]，故障发生点距离整流侧测距装置出的距离x与到达整流侧和逆变侧测距装置处某一频率下的故障电压幅值比之间存在关系

式中，L为直流输电线路线路全长；αj为线路j模衰减常数（j=0或1，分别表示零模和线模）；、分别表示整流侧和逆变侧测距装置处检测到的来自于故障源的频率为f的故障电压幅值。

当线路发生接地故障时，在故障点和母线处因其线路波阻抗不连续而会出现行波折反射。在一定的时间窗内，线路两端测距装置处检测到的行波信号中就含有故障初始行波、故障点反射波和母线发射波[11]。因此，在测距装置处提取单一频率的来自故障源的行波信号存在困难。

以小波变换为代表的各类信号时频分析方法，对仿真波形的波头标定获得了较为满意的结果，特别是基于小波模极大值理论的波头标定方法对初始故障行波波头标定效果显著[12-16]。小波变换的模极大值与信号的突变点一一对应，其大小表示突变点的变化强度[17]。由于初始故障行波波头获得方便而且效果良好，对单一频率的故障信号的衰减分析转化为对故障行波首波头的衰减分析。用到达整流侧和逆变侧的故障行波首波头幅值比代替特定频率下的线路两端来自故障源的高频分量幅值比，式（3）变为

式中，Uja、Ujb分别表示同一频带下整流侧测距装置处和逆变侧测距装置处检测到的故障电压行波j模分量首波头幅值；表示该波头对应频率下的j模线路衰减常数。

线路衰减常数是关于频率的非线性函数[18]，对于直流输电线路，如果能准确确定单位长度线路的电阻、电感、电容和电纳，就可以求得任意频率下线路衰减常数。这样通过求得特定频带下到达整流侧和逆变侧测距装置处的故障电压j模分量首波头幅值比，利用式（4）就可以计算出故障发生点距离整流侧测距装置处的距离，从而实现故障测距的目的。实际上，高压线路沿线地质条件相当复杂，不同的地质段的土壤电阻率有不同的取值，线路的分布电感也会因不同的地区和线路结构而产生差异，同时，由于气候的影响，沿线的不均匀电晕分布影响了线路的分布电容，所以对于特定的直流输电线路，准确测量线路的实际参数存在困难[19]，所以准确求取线路的衰减常数存在一定的困难。

由上述分析可知，对于特定的直流输电线路，由于线路衰减常数不能够准确确定，通过求取同一频带下整流侧测距装置处和逆变侧测距装置处检测到的故障电压行波j模分量首波头幅值比来实现故障测距存在一定的误差。分析式（4）可知，x与之间存在确定的非线性关系，如果能够确定的这种数学关系，就能够通过线路两端的测量装置，测量故障电压行波j模分量首波头幅值，就可以实现故障测距。

由于线路衰减常数与频率相关，当频率很低时线路衰减常数很小，当频率较大时，线路衰减常数较大。根据式（4）可以得到

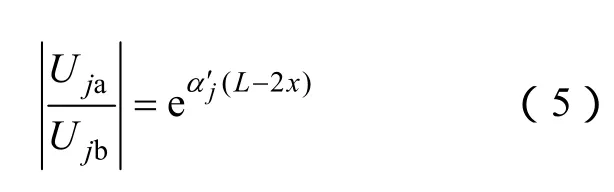
图2 故障点在线路中点附近，各尺度下两侧故障电压行波首波头幅值比与故障距离之间的关系图Fig.2 The relationship between fault distance and the ratio of amplitude of initial traveling wave head in rectifier side to which in the inverter side under different wavelet levels when fault points vary in nearby midpoint of transmission line

分析图2可知，当故障点在线路中点附近变化时，故障电压行波线模分量低频部分（如图中a6）内的首波头幅值比几乎不变，故障电压行波线模分量高频部分（如图中d1、d2、d3、d4）内的首波头幅值比非线性变化。因此故障电压行波线模分量低频部分内的首波头幅值比的大小不能准确反映故障位置，而故障电压行波线模分量高频部分内的首波头幅值比大小能反映出故障位置，故应该选用故障电压行波线模分量高频部分内的首波头幅值比作为故障测距特征量。

图 3a～图 3d分别表示的是，故障点在全线范围内变化时，线路上发生金属性接地故障下，d1、d2、d3、d4对应的频带内线路两端测得的故障电压行波线模分量首波头幅值比与故障距离之间的关系图。

图3 故障点在线路全线范围内，各尺度下两侧故障电压行波首波头幅值比与故障距离之间的关系图Fig.3 The relationship between fault distance and the ratio of amplitude of initial traveling wave head in rectifier side to which in the inverter side under different wavelet level when fault points vary in the whole transmission line

分析图 3a～图 3d可知，在各频带内，线路两端电压行波首波头幅值比与故障距离之间总体上呈现非线性确定关系，且频带越高线路两端电压行波线模分量首波头幅值比越大。

3 基于高频量衰减特性的特高压直流输电线路神经网络双端故障测距算法

由式（4）及上文分析可知，故障距离由整流侧测距装置处和逆变侧测距装置处检测到的故障电压行波j模分量高频部分首波头幅值比与该波头对应频率下的j模线路衰减常数决定，但线路衰减常数准确计算存在一定的困难。现设定距离整流侧测距装置400km发生非金属性接地故障，过渡电阻为1Ω。利用文献[9]提出的传统双端测距方法，根据通过实验方法得到的=0.000 576 166，以及测得的d1频带内整流侧暂态电压线模分量首波头模极大值230.8，逆变侧暂态电压线模分量首波头模极大值 160.2，可求得故障距离为 392.14km，误差为-7.86km。过渡电阻为1Ω在线路其他点故障时，测距结果见表1。

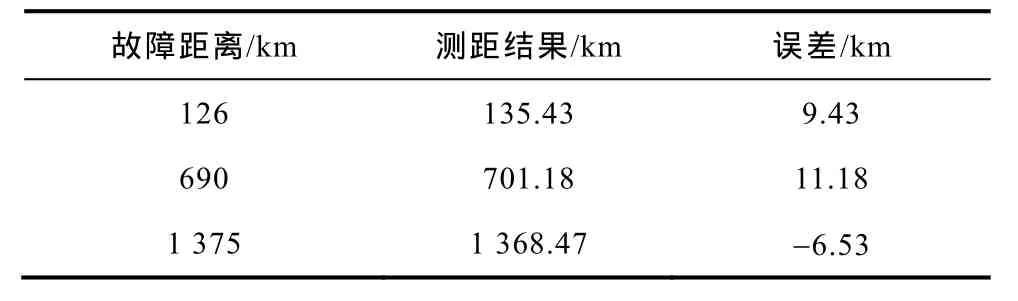
表1 传统双端测距结果Tab.1 The results of fault location used traditional two terminal fault location method

分析表1中仿真结果可知，传统通过实验方法先求线路衰减常数，再根据测得的首波头幅值比，利用式（4）求得测距结果的方法存在一定的误差，这是因为通过实验方法求得的线路衰减常数并不精确，而且要准确求得实际输电系统的线路衰减常数将更为困难。因此，寻找一种不计算线路衰减常数也能准确得到故障距离的计算方法对本文提出的故障测距原理的实现至关重要。人工神经网络具有很强的非线性函数逼近拟合能力，利用人工神经网络的方法将不必准确计算线路衰减常数也能准确实现故障定位。故可采用神经网络对x与之间的非线性关系进行泛化分析，从而实现对故障位置进行测算。

3.1 BP神经网络

目前，在人工神经网络的实际应用中，绝大部分的网络模型采用的是 BP网络及其变化形式，理论上已经证明，具有一个隐含层的三层网络可以逼近任意非线性函数[20]，本文采用单隐层 BP网络模型。BP网络由输入层、隐含层和输出层三层组成，其基本思想是对一定量的样本（输入和期望输出）进行学习，即将输入送至网络输入层的各个神经元，经隐含层和输出层计算后，输出对应的预测值，如果预测值与期望输出之间的误差不满足精度要求，则从输出层反向传播该误差，然后进行权值和阀值的调整，使得网络的实际输出和期望输出间的误差逐渐减小，直至满足精度要求，因此 BP网络的核心是通过一边向后传递误差一边修正误差的方法来不断调节网络参数（权值和阈值），以逼近所希望的输入、输出之间的映射关系。

3.2 基于直流输电线路双端量的神经网络测距算法

样本的选取和预处理是神经网络模型建立的关键[21]。对于直流输电线路故障测距而言，训练样本集要尽可能全面反映不同故障类型和不同故障距离下线路两端电压首波头幅值比特征，同时也要考虑神经网络本身的泛化性能。本文测距神经网络模型训练集组织步骤为：

（1）取首波头到达后5ms时窗内的线路两端暂态电压信号作为故障信号，对其进行解耦变换得到独立的暂态电压线模分量。分别对整流侧和逆变侧测距装置处得到的暂态电压线模分量进行小波变换，得到整流侧第1、2、3、4尺度下的高频带内的暂态电压线模分量首波头幅值U1a1、U1a2、U1a3、U1a4，以及对应频带内的到达逆变侧的暂态电压线模分量首波头幅值U1b1、U1b2、U1b3、U1b4。分别求取各个频带内的两端暂态电压线模分量首波头幅值比。训练样本的输入矢量p=［p1,p2,p3,p4］。

（2）仿真时选用的是云广±800kV特高压直流输电系统实际参数仿真模型，根据实际参数建立的仿真模型能很好地模拟云广特高压直流输电系统。为了使得训练集能够包含不同故障距离下故障特征，从距离整流侧保护安装处5km开始设置故障点，故障距离步长取为10km，故障点设置一直到距离整流侧保护安装处1 415km结束，共包含142组故障数据。

（3）过渡电阻为0～100Ω，步长为10Ω。

（4）由于训练样本集的输入矢量数值有很大的差异，对于某一输入节点，如果该节点的数值过大，这样的隐含层的输出中，该节点的权值的影响就要比其他分量大很多，这样其他分量就会失去调控作用[23]。所以有必要对输入矢量进行归一化处理，使得输入矢量变化范围为（0，1），这样在神经网络训练时，各个输入矢量具有同等重要的地位。

经过上述步骤，构建的故障测距神经网络模型如图4所示。

该网络具有一个隐含层，输入层神经元数目为4，对应的是四个频带内整流侧和逆变侧测距装置处检测到的故障电压行波首波头幅值比，隐含层神经元数目为15，输出层神经元数目为1，对应的是故障距离，因此网络的拓扑结构为 4×15×1。ωml表示输入层的第m个神经元到隐含层的第l个神经元之间的连接权值，lω表示隐含层第l个神经元到输出层神经元之间的权值。

图4 故障测距BP神经网络模型Fig.4 BP neural network for fault location

神经网络采用自适应学习速度算法，学习率为0.01，最大训练次数取为 10 000，收敛精度设置为10-5。训练收敛曲线如图 5所示，可见经过 1 067次训练后，神经网络的误差收敛至预期要求，该神经网络收敛速度较快。

4 仿真

参照云广特高压直流输电系统换流站主接线及其参数，根据云广特高压直流输电系统元件模型，可以建立云广±800kV特高压直流输电系统仿真模型。云广特高压直流输电系统电压等级为±800kV，直流额定功率5 000MW，直流额定电流3.125kA。直流输电线路全长 1 418km，沿线大地电阻率平均值为 1 000Ω·m，采用 6×LGL—630/45导线，采用Frequency Dependent（Phase）Model Options模型。云广±800KV特高压直流输电控制系统是基于CIGRE直流输电标准测试系统来建立，为满足云广±800kV特高压直流输电系统控制的需要，对CIGRE直流输电标准测试系统的控制系统做了部分改动。仿真模型如图6所示。

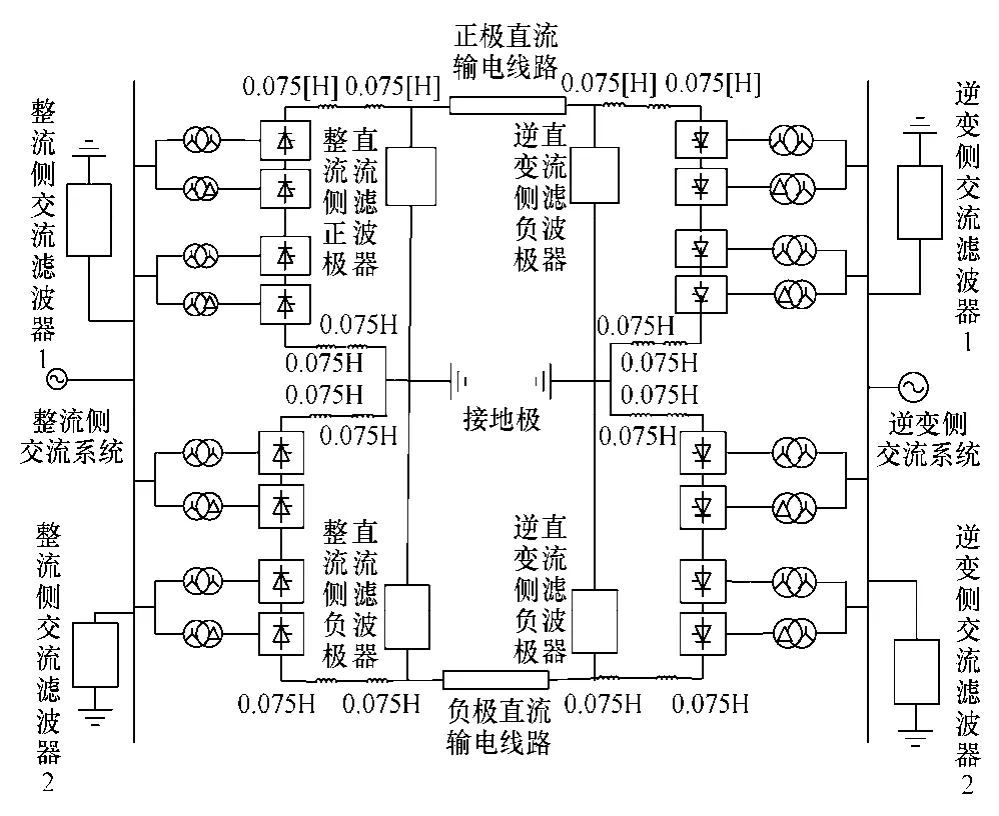
图6 云广特高压直流输电仿真模型Fig.6 Simulation model of Yunnan-Guangdong UHVDC

本文选取暂态电压线模分量作为仿真数据对测距算法进行验证。故障测距神经网络模型形成以后，将反映故障位置的特征数据输入训练后的网络模型即可实现故障测距，例如线路上距离整流侧测距装置 400km发生非金属性接地故障，过渡电阻为1Ω，利用基于神经网络的测距方法，根据测得的d1、d2、d3、d4频带内的暂态电压线模分量首波头幅值 1.440 7、1.412 7、1.360 5、1.326 7，得到测距特征量p=(1.440 7, 1.412 7, 1.360 5, 1.326 7)，将其输入训练后的神经网络测距模型得到测距结果为399.85km，测距误差为-0.15km，可见利用基于神经网络的测距方法进行故障测距不用计算线路衰减常数，而且精度较高。

故障测距 ANN模型是否具有实用价值，测试集应通过变化各种因素并避开训练集，以此综合测试和评定神经测距模型的泛化能力。表2给出了利用传统双端测距方法（文献[9]提出的双端测距方法）和基于神经网络的测距方法对训练集以外的不同故障距离进行测距得到的结果。

分析表2中仿真结果可知，由于通过实验的方法得到的线路衰减常数并不准确，传统的双端测距方法存在较大的误差，而且在某些故障点处测距方法失效。而在不同过渡电阻下不同故障距离处，利用故障测距 ANN模型测得的结果误差基本保持在2km以内，而且随着过渡电阻的变化，测距精度不受影响，可见本文提出的基于高频量衰减特性的特高压直流输电线路神经网络双端故障测距方法精度较高，而且耐受过渡电阻能力强。

表2 测距结果Tab.2 The results of fault location

5 结论

选用四个高频带内的线路两端故障电压行波线模分量首波头幅值比作为神经网络模型的输入样本集、故障距离作为输出样本集，对神经网络进行训练、测试，形成直流输电线路故障测距神经网络模型。将故障数据输入训练后故障网络测距模型即可实现故障测距。本文得到以下结论：

（1）故障距离与到达整流侧和逆变侧测距装置处的故障电压行波线模分量高频部分首波头幅值比之间存在确定的非线性关系。

（2）基于神经网络的高压直流输电线路双端故障测距方法只是利用了故障后一段时窗内的双端故障数据，求取特定频带下的两端电压行波线模分量高频部分首波头幅值比即可实现故障测距，而不依赖于行波在故障点与测量点之间的传输时间和传输速度，从而避免了传统的双端行波测距方法中波速度确定困难以及对两端时钟同步装置精度要求过高等问题。

（3）该基于高频量衰减特性的特高压直流输电线路神经网络双端故障测距方法不依赖对线路衰减常数的准确计算，精度较高，而且耐受过渡电阻能力强。

[1] 李立浧. 直流输电技术的发展及其在我国电网中的作用[J]. 电力设备, 2004, 5(11): 1-3.

Li Licheng. Development of HVDC transmission technology and its role in power network in China[J].Electrical Equipment, 2004, 5(11): 1-3.

[2] 刘海峰, 徐政, 金丽成. 世界远距离大容量高压直流输电工程可靠性调查综述[J]. 高压电器, 2002,38(3): 1-4.

Liu haifeng. Xu zheng, Jin Licheng. A review of the reliability survey of long distance high power HVDC transmission project throughout the world[J]. High Voltage Apparatus, 2002, 38(3): 1-4.

[3] 宋国兵, 蔡新雷, 高淑萍, 等. 高压直流输电线路故障定位研究综述[J]. 电力系统保护与控制, 2012,40(5): 133-138.

Song Guobing, Cai Xinlei, Gao Shuping, et al. Survey of fault location research for HVDC transmission lines[J]. Power System Protection and Control, 2012,40(5): 133-138.

[4] 廖凯, 何正友, 李小鹏. 基于行波固有频率的高压直流输电线路故障定位[J]. 电力系统自动化, 2013,37(3): 104-108.

Liao Kai, He Zhenyou, Li Xiaopeng. The fault location method of UHVDC transmission line which based on traveling wave natural frequency[J]. Automation of Electric Power Systems, 2013, 37(3): 104-108.

[5] 王钢, 李志铿, 李海锋. ±800kV特高压直流输电线路暂态保护[J]. 电力系统自动化, 2007, 31(21):40-43.

Wang Gang, Ling Zhikeng, Li Haifeng. Transient based protection for ±800kV UHVDC transmission lines[J]. Automation of Electric Power Systems, 2007,31(21): 40-43.

[6] 张保会, 张嵩, 尤敏, 等. 高压直流线路单端暂态量保护研究[J]. 电力系统保护与控制, 2010, 38(15):18-23.

Zhang Baohui, Zhang Song, You Min, et al. Research on transient based protection for HVDC line[J].Power System Protection and Control, 2010, 38(15):18-23.

[7] 哈恒旭, 于洋, 张旭光, 等. 考虑频率相关参数的直流输电线路故障特征分析[J]. 电力系统自动化,2012, 36(16): 70-75.

Ha Hengxu, Yu Yang, Zhang Xuguang, et al. Frequency characteristics of fault transients for HVDC transmission line with frequency dependent distributed parameters[J]. Automation of Electric Power Systems,2012, 36(16): 70-75.

[8] 张怿宁, 徐敏, 刘永浩, 等. 考虑波速变化特性的直流输电线路行波故障测距新算法[J]. 南方电网技术, 2011, 35(7): 227-232.

Zhang Yining, Xu Min, Liu Yonghao, et al. A novel travelling wave fault location algorithm for HVDC transmission lines considering variation characteristics of wave speed[J]. Southern Power System Technology,2011, 35(7): 227-232.

[9] 陈仕龙, 张杰, 毕贵红, 等. 基于高频量衰减特性的特高压直流输电线路故障测距方法[J]. 电力系统保护与控制, 2014, 42(10): 1-7.

Chen Shilong, Zhang Jie, Bi Guihong, et al. A fault location method based on high frequency attenuation characteristic of UHVDC transmission line[J]. Power System Protection and Control, 2014, 42(10): 1-7.

[10] 施围, 郭洁. 电力系统过电压计算[M]. 北京: 高等教育出版社, 2006.

[11] 吴昊, 肖先勇, 邓武军. 输电线行波测距中雷击与短路故障的识别[J]. 高电压技术, 2007, 33(6): 63-67.

Wu Hao, Xiao Xianyong, Deng Wujun. Identification of lightning strike and fault in the traveling wave location of transmission line[J]. High Voltage Engineering, 2007, 33(6): 63-67.

[12] 董新洲, 葛耀中, 徐丙垠. 利用暂态电流行波的输电线路故障测距研究[J]. 中国电机工程学报, 1999,19(4): 76-80.

Dong Xinzhou, Ge Yaozhong, Xu Bingyin. Research of fault location based on current travellingwaves[J].Proceedings of the CSEE, 1999, 19(4): 76-80.

[13] 覃剑, 陈祥训, 郑健超, 等. 利用小波变换的双端行波测距新方法[J]. 中国电机工程学报, 2000,20(8): 6-10.

Qin Jian, Chen Xiangxun, Zheng Jianchao, et al. A new double terminal method of travelling wave fault location using wavelet transform[J]. Proceedings of the CSEE, 2000, 20(8): 6-10.

[14] 张小丽, 曾祥君, 马洪江, 等. 基于 Hilbert-Huang变换的电网故障行波定位方法[J]. 电力系统自动化,2008, 32(8): 64-68.

Zhang Xiaoli, Zeng Xiangjun, Ma Hongjiang, et al.Power grid faults location with travel ing wave based on Hilbert Huang transform[J]. Automation of Electric Power Systems, 2008, 32(8): 64-68.

[15] 张峰, 梁军, 车仁飞. 弱行波信号的奇异点检测方法[J]. 电力系统自动化, 2010, 34(8): 92-96.

Zhang Feng, Liang Jun, Che Renfei. A novel singularitypoint detection method for weak traveling wave signals[J]. Automation of Electric Power Systems,2010, 34(8): 92-96.

[16] 张广斌, 束洪春, 于继来. 基于 Hough 变换直线检测的行波波头标定[J]. 中国电机工程学报, 2013,33(19): 165-173.

Zhang Guangbin, Shu Hongchun, Yu Jilai. Surge identification for travelling wave based on straight lines detection via hough transform[J]. Proceedings of the CSEE, 2013, 33(19): 165-173.

[17] 何正友. 小波分析在电力系统暂态信号处理中的应用[M]. 北京: 中国电力出版社, 2011.

[18] Marti J R. Accurate modeling of freguency dependent transmission line inelectromagnetic transient simulations[J]. IEEE Transactions on Power Apparatus and System, 1982, 101(1): 147-157.

[19] 黄雄, 王志华, 尹项根, 等. 高压输电线路行波测距的行波波速确定方法[J]. 电网技术, 2004, 28(19):34-37.

Huang Xiong, Wang Zhihua, Yin Xianggen, et al.Travelling wave velocity measurement in fault location based ontravelling wave for high voltage transmission line[J]. Power System Technology, 2004, 28(19): 34-37.

[20] 束洪春, 邬乾晋, 张广斌, 等. 基于神经网络的单端行波故障测距方法[J]. 中国电机工程学报, 2011,31(4): 85-92.

Shu Hongchun, Wu Qianjin, Zhang Guangbin, et al.Single terminal traveling wave fault location method based on ANN[J]. Proceedings of the CSEE, 2011,31(4): 85-92.

[21] 毛鹏, 孙雅明, 张兆宁. 具有冗余神经元神经网络模型系统的输电线路故障测距研究[J]. 中国电机工程学报, 2000, 20(7): 28-33.

Mao Peng, Sun Yaming, Zhang Zhaoning. Study of fault location for high voltage over-head transmission line using neural networks model system with redundant neuron[J]. Proceedings of the CSEE, 2000, 20(7): 28-33.

[22] 束洪春, 段瑞敏, 田鑫萃, 等. 一种利用自然频率和人工神经网络的配网故障测距方法[P]. 中国,CN102129103A, 201-07-20.