零电压导通、零电压关断单管无线电能传输电源

王春芳 陈杰民 李 聃 孙 会

（1. 青岛大学自动化工程学院 青岛 266071 2. 海尔集团技术研发中心 青岛 266103）

1 引言

随着电力电子技术的发展，制约互感耦合式无线电能传输（简称 IPT）电源实用化的一些关键技术诸如谐振参数、谐振频率、补偿方式和稳定性等正逐步被科研人员所突破[1-6]。然而，传统的IPT电源拓扑电路一般只能实现一种软开关方式即电流型电路只能实现零电压导通，电压型电路只能实现零电流关断[7-9]，致使电源的传输效率无法进一步提高；另外，为提高电源的功率因数，通常在传统IPT电源的一次增加锁相环电路，使线圈工作在谐振状态，但是该方法会出现频率分差现象，导致系统稳定性降低[10-13]。目前在1kW以内的功率传输场合，主电路一般采用半桥电路或者推挽电路，大于1kW的场合大多采用全桥电路[5,6]。对于追求低成本、高可靠性和大量生产的家电领域用IPT电源来说，由以上拓扑电路制作的产品仍显得体积大、成本高，难以被广泛普及。然而现有技术生产的单管型 IPT产品，由于传输功率较小，其应用仅局限于为手机、平板电脑等小功率电器充电的场合[14-16]。为此有必要突破现有技术瓶颈，寻求一款传输功率在1kW左右且具有低成本、高可靠性、高效率和高功率因数的家电领域用单管型IPT电源。

针对上述问题，本文提出了一种用单个开关管逆变就能实现IPT的电源。该电源主电路一次侧借鉴了并联谐振式电磁炉的一次电路，而其二次电路和电磁炉截然不同。电磁炉的二次线圈由一次线圈在电炒锅上形成的涡流环形成，通过涡流发热来加热食物；而所提出的IPT电源的二次侧由距离30mm的感应线圈、并联补偿电容、高频全桥整流桥、滤波电容和厨用豆浆机（或果蔬机）负载组成，电机负载需要有效值220V、100Hz的正弦波为其供电。电磁炉在控制上仅需固定的脉宽+暂载率控制即可，而所提方案采用PWM+PFM组合的控制方法，既可使开关管实现零电压导通和零电压关断，又使系统在开关管导通和关断期间均可传输能量，从而降低了开关损耗，增加了可靠性，突破了单管电源输出功率小的技术瓶颈，其传输功率可达1kW，保证了电能的高效利用。与同功率的半桥和全桥 IPT电源相比，单管IPT电源由于只有一个开关管且在导通和关断时都实现了软开关，具有电路结构简单、体积小、成本低、可靠性和效率高的特点，仿真及实验均表明了上述特点。

2 所研究的IPT电源系统

2.1 IPT电源的系统结构

所研究IPT电源的系统结构图如图1所示。电感Li和电容Ci组成LC滤波电路，用于提高电路的功率因数，代替传统IPT电源里的锁相环电路；电阻R1和R2组成电压检测电路，用于检测LC滤波后的电压，由此判断IPT电源的输入电压是否过电压或欠电压；一次发射线圈Lp、一次补偿电容Cp、二次接收线圈Ls及二次补偿电容Cs组成谐振耦合网络，Cp对Lp进行谐振补偿；Cs对Ls进行谐振补偿，并通过Vce检测电路实现开关管Q的零电压导通和零电压关断。单片机控制电路用于控制功率传输，并通过驱动电路，控制开关管Q。

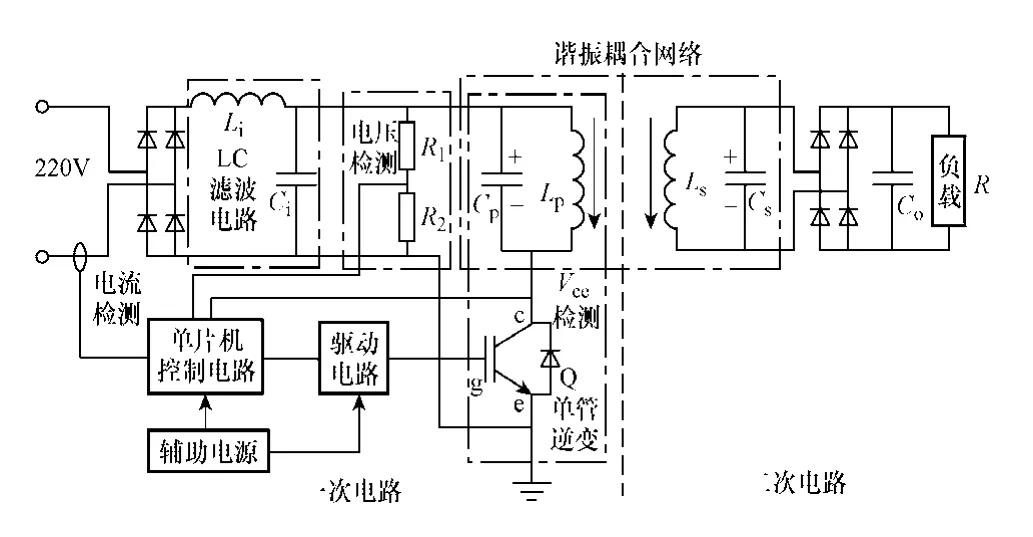
图1 系统结构Fig.1 System structure diagram

AC220V经全桥整流、LC滤波后转换成峰值310V的电压，单管逆变电路将该电压转换为高频方波电压并施加到Lp的两端，由Lp将能量传递给Ls，Ls两端的电压经全桥整流和电容Co滤波后转换成有效值为 220V的电压供负载使用。电压检测电路和电流检测电路一起用于调控电源的输出功率。

2.2 IPT电源的工作过程

图2为所研究IPT电源的工作过程波形图。

（1）阶段 1（t0～t1）。在这一阶段，驱动信号Vge由低电平变为高电平，由于电感电流iLp为负，开关管Q的二极管导通。

（2）阶段 2（t1～t2）。电感电流iLp由负变正，开关管 Q导通，电感电流iLp流经开关管 Q，由于电容Cp电压pCV˙等于输入电压，开关管电流Ice近似线性增加。

（3）阶段3（t2～t3）。驱动信号Vge由高电平变为低电平，开关管 Q关断，电感电流iLp由电容Cp续流，由于电容Cp电压pCV˙缓慢下降，开关管耐压Vce缓慢上升，因此，开关管Q为零电压关断。从t2时刻起，电感Lp与电容Cp进入谐振状态。

（4）阶段 4（t3～t4）。到t3时刻，电容Cp电压放电到零，电感电流iLp给电容Cp反向充电，到t4时刻，电容Cp电压pCV˙谐振到最大值，此时开关管Q耐压Vce达到最大值。

（5）阶段 5（t4～t5）。到t4时刻，电感电流iLp变向，电容Cp开始放电，开关管 Q耐压降低；到t5时刻，电容Cp电压VCp放电到零，电感电流iLp依然为负。

（6）阶段 6（t5～t6）。t5时刻之后，电感Lp又给电容Cp充电，电容电压上升；到t6时刻，电容电压pCV˙上升为输入电压，并钳位到此值，此时开关管耐压降Vce=0，由于电感电流iLp仍旧为负，开关管的体二极管导通。

（7）阶段 7（t6～t7）。此阶段为死区时间，t7时刻，驱动信号Vge再次到来，由于电感电流iLp依旧为负，且开关管Q的体二极管已经导通，因此实现开关管的零电压导通。至此，一个开关周期结束。

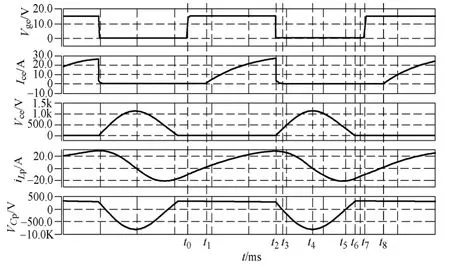
图2 主电路工作波形Fig.2 Operating waveforms of the main circuit

2.3 IPT电源的主电路建模

通过互感模型法对主电路进行分析，可得图 3所示IPT电源主电路的等效电路。该图由直流输入、开关网络、谐振耦合网络、二次全桥整流、电容滤波和直流输出组成。图3中i.FHAu˙ 为谐振网络的输入电压，Rp、Rs分别为一次、二次线圈内阻，M为发射线圈Lp与接收线圈Ls的互感，Ro为负载电阻，R为等效负载，Zs为二次回路等效阻抗，Ze为二次回路等效到一次电路的等效阻抗。谐振耦合网络的一次发射线圈采用并联电容Cp补偿，二次接收线圈采用并联电容Cs补偿[17-19]。其中，Cp采用耐压较高的电容，Cs采用耐流较大的电容，且Cp、Cs的频率稳定性都较高。

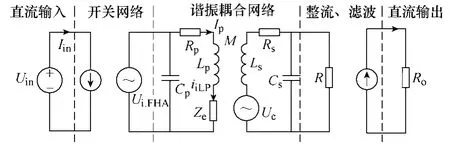
图3 主电路的等效电路Fig.3 The equivalent circuit diagram of the main circuit

通过对图3所示的等效电路进行建模和分析，并根据文献[4,7]的推导方式可推导出

谐振网络的输入电压为

由于i.FHAu˙ 为一方波电压，其基波分量有效值为

二次接收线圈产生的电压为

由此可得输出电压为

由式（5）和式（8）可得谐振网络的电压增益为

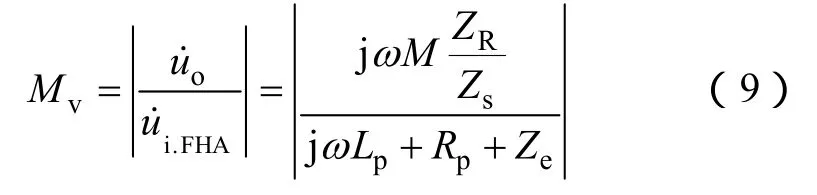
利用Mathcad软件可得如图4所示直流增益MV随不同参数变化的曲线，其中a=LpLs。

图4 电压增益变化曲线Fig.4 Voltage gain curves

根据图4所示的电压增益随不同参数变化的曲线可进行谐振网络参数的优化设计。

2.4 IPT电源的谐振参数设计

（1）二次谐振频率的设计。为了使IPT电源的输出功率达到最大，需要将接收线圈Ls和二次补偿电容Cs的谐振频率设置在开关管 Q的开关频率fs处，即开关频率。

（2）一次谐振频率的设计。由文献[5]可知一次补偿电容Cp需满足

式中，fp为发射线圈Lp与一次补偿电容Cp的谐振频率。

由图2所示主电路工作过程可知，要使开关管Q实现零电压导通，需保证在驱动信号到来之前，一次补偿电容的电压谐振到输入电压。故通常一次谐振频率fp只需略大于开关频率fs，这样方可保证零电压导通。但是在本设计中，由于pCV˙在t2、t6时刻对应的电压为输入电压，不为0，故一个周期内，Lp、Cp实际的谐振时间大于半个一次谐振周期，其真正半个谐振周期所对应的时间为t3～t5，故fp明显大于fs，因此在设置fp时，需要特别注意。

2.5 IPT电源的输出电压控制

由图4所示电压增益曲线可知，当输出电压变化时，为得到稳定的输出电压需相应地改变开关管工作频率fs。但随着fs接近一次谐振频率fp，图 2中t6～t7所对应的死区时间逐渐减小，直到某一频率，开关管无法再实现零电压导通，导致开关损耗急剧增加，从而使效率显著降低。

为保证一定的死区时间，增加Vce检测电路，当检测到Vce下降到0与Vge变为高电平之间的时间差减小到一定值时，降低驱动信号Vge的占空比，以便能继续增加开关管工作频率fs。这样通过变频+变占空比的控制方式便可达到控制输出电压稳定的目的。

3 仿真与实验

为验证所提出的电路拓扑及其控制方法的可行性和正确性，对所设计的电源进行了仿真和实验。图 5为采用 Saber仿真软件进行的仿真。其中Vge为驱动波形，id为开关管Q的体二极管电流，Ice为流过开关管Q的电流，Vce为施加在开关管上的电压。

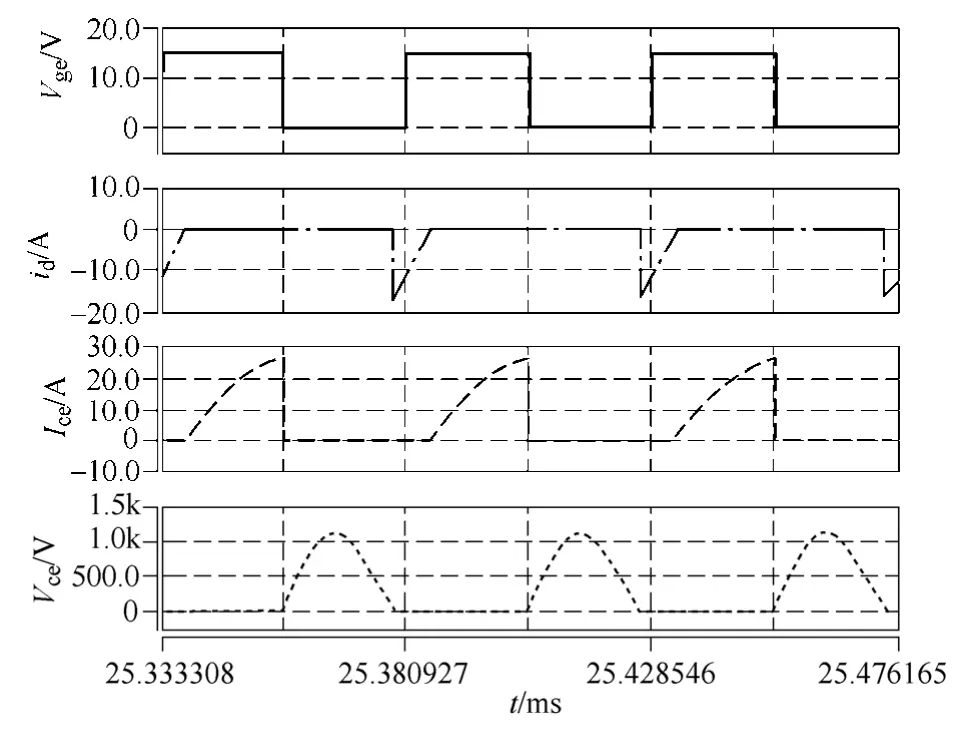
图5 主电路仿真波形Fig.5 Simulation waveforms of the main circuit

由图5可知，在Vge变为高电平之前，Vce已降为0，且开关管Q的体二极管已经导通，故可实现零电压导通；在驱动信号Vge关断之后，开关管耐压Vce缓慢上升，同时也实现了零电压关断。

根据本文所论述的设计方法，设计了一台额定功率为1kW的为厨房用无尾豆浆机（或果蔬机）供电的IPT电源样机。尽管在输入端采用较小的整流滤波电容，但通过PFC+PWM控制，在负载变化时也能保证无线电能传输电源的输出基本稳定。其主要的设计参数如下：输入交流电压为 180～264V/50Hz，输出电压有效值为220V、100Hz的正弦波，一次发射线圈电感Lp=220μH，二次接收线圈电感Ls=50μH，一次补偿电容Cp=160nF，二次补偿电容Cs=1 100nF，一次、二次线圈距离为30mm，一次、二次线圈互感为35μH。

图6为所设计IPT电源样机的软开关实验波形。由图 6可知，当驱动信号Vge变为高电平之前，开关管耐压Vce已降为0，实现了零电压导通；驱动信号Vge变为低电平之后，开关管耐压Vce缓慢上升，开关管同时能够实现零电压关断。

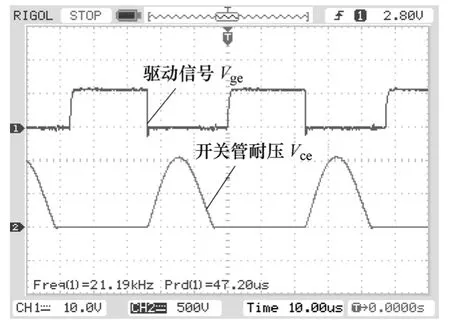
图6 软开关波形Fig.6 Soft switching waveforms

图7为当一次、二次线圈中心对齐，且距离设定为30mm时，输入电压和输入电流的波形。由图7可知输入电流为正弦波，且输入电压和输入电流同相位，因此样机的功率因数较高。

图7 输入电压、电流波形Fig.7 The input voltage and current waveforms

当一次、二次线圈垂直距离为30mm定值而中心偏移时，测量IPT电源的功率因数和效率，并分别绘制成对应的曲线。图8为功率因数随中心偏移距离变化的曲线。由图8可知，当线圈中心偏移在40mm内时，电源的功率因数在0.98以上。由此可知当输入端采用较小的无极性整流滤波电容时，对用该系统不仅不影响输出波形，而且具有较高的功率因数。

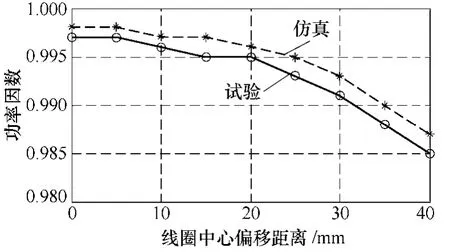
图8 功率因数随线圈中心偏移变化Fig.8 Power factor changing with the coil center offset

图9为效率随线圈中心偏移距离变化的曲线。

图9 效率随线圈中心偏移变化Fig.9 Efficiency changing with the coil vertical offset

由图9可知，当线圈中心偏移在15mm内时，效率在0.890～0.895之间，偏移量在35mm内时，效率在0.85以上。由此可知，在实际应用中当一二次线圈垂直距离为30mm定值（橱柜台面厚度）不变而中心偏移在40mm内时，电源均具有较高的工作效率。其原因分析为：①主电路只有一个开关管，且实现了零电压导通和零电压关断，减少了开关损耗，提高了效率。②在PFM+PWM的控制方式下，主电路参数的选取较为合适，在负载急剧变化的情况下既保证了输出的稳定性，也提高了传输效率。

4 结论

通过仿真和实验验证，给出如下结论：

（1）所提出的单管逆变电路通过零电压导通和零电压关断并辅以变频+变占空比的功率传输控制可以制作成1kW等级的IPT电源，其具有元器件少、体积小、成本低、效率高及可靠性高等优点。

（2）在所提方案中采用 LC滤波电路代替传统的锁相环电路用于提高功率因数，具有电路简单、功率因数高的优点。

（3）所提出电路拓扑的参数设计方法和功率传输控制方法证明是正确的和行之有效的。

（4）所提IPT方案除可用作家用电器领域的无线电能传输电源外，还可在对二次电路稍加改动后用于同样功率等级的无线充电设备上。

[1] 孙跃, 赵志斌, 王智慧, 等. 用于感应电能传输系统的新型软开关电路[J]. 电工技术学报, 2013,28(8): 128-134.

Sun Yue, Zhao Zhibin, Wang Zhihui, et al. A new circuit of soft-switching inductive power transfer system[J]. Transactions of China Electrotechnical Society,2013, 28(8): 128-134.

[2] 武瑛, 严陆光, 徐善纲. 新型无接触电能传输系统的稳定性分析[J]. 中国电机工程学报, 2004, 24(5):63-66.

Wu Ying, Yan Luguang, Xu Shangang. Stability analysis of the new contactless power delivery system[J]. Proceedings of the CSEE, 2004, 24(5): 63-66.

[3] 孙跃, 夏晨阳, 戴欣, 等. 感应耦合电能传输系统互感耦合参数的分析与优化[J]. 中国电机工程学报,2010, 30(33): 44-50.

Sun Yue, Xia Chenyang, Dai Xin, et al. Analysis and optimization of mutual inductance for inductively coupled power transfer system[J]. Proceedings of the CSEE, 2010, 30(33): 44-50.

[4] 周雯琪, 马皓, 何湘宁. 感应耦合电能传输系统不同补偿拓扑的研究[J]. 电工技术学报, 2009, 24(1):133-139.

Zhou Wenqi, Ma Hao, He Xiangning. Investigation on different compensation topologies in inductively coupled power transfer system[J]. Transactions of China Electrotechnical Society, 2009, 24(1): 133-139.

[5] Boys J T, Covic G A, Green A W. Stability and control of inductively coupled power transfer systems[J]. IEE Proceedings-Electric Power Applications,2000, 147(1): 37-43.

[6] 武瑛. 新型无接触供电系统的研究[D]. 北京: 中国科学院研究生院, 2004.

[7] 夏晨阳. 感应耦合电能传输系统能效特性的分析与优化研究[D]. 重庆: 重庆大学, 2010.

[8] 孙跃, 夏晨阳, 赵志斌, 等. 电压型 ICPT 系统功率传输特性的分析与优化[J]. 电工电能新技术,2011, 30(2): 9-12.

Sun Yue, Xia Chenyang, Zhao Zhibin, et al. Analysis and optimization on power transmission characteristics for voltage-fed ICPT system[J]. Advanced Technology of Electrical Engineering and Energy, 2011, 30(2):9-12.

[9] 杨民生, 王耀南, 欧阳红林, 等. 基于可控电抗器的无接触电能传输系统动态补偿[J]. 电工技术学报,2009, 24(5): 183-189.

Yang Minsheng, Wang Yaonan, Ouyang Honglin,et al. Dynamic compensation of contact-less power transmission system based on controlled reactor[J].Transactions of China Electrotechnical Society, 2009,24(5): 183-189.

[10] 李宏, 贺昱曜, 王崇武. 一种全桥负载串联谐振逆变器谐振频率跟踪和输出功率控制方法[J]. 电工技术学报, 2010, 21(7): 93-99.

Li Hong, He Yuyao, Wang Chongwu. A new method of frequency tracking and output power control for full bridge series load resonant inverter[J]. Transactions of China Electrotechnical Society, 2010, 21(7):93-99.

[11] 李亚斌, 彭咏龙, 李和明. 提高串联型逆变器频率跟踪速度的研究[J]. 电工技术学报, 2004, 19(11):78-81.

Li Yabin, Peng Yonglong, Li Heming. Research on increasing frequency-tracking speed for series resonant inverter[J]. Transactions of China Electrotechnical Society, 2004, 19(11): 78-81.

[12] Wang C S, Stielau O H, Covic G A. Design considerations for a contactless electric vehicle battery charger[J]. IEEE Transactions on Industrial Electronics, 2005,52(5): 1308-1314.

[13] 孙跃, 杨芳勋. 基于移相直通控制策略的 IPT系统输出功率调节[J]. 电工技术学报, 2012, 27(10): 6-12.

Sun Yue, Yang Fangxun. Regulation of inductive power transfer system based on phase shifting-short control strategy[J]. Transactions of China Electrotechnical Society, 2012, 27(10): 6-12.

[14] Kim C G, Seo D H, You J S, et al. Design of a contactless battery charger for cellular phone[J].IEEE Transactions on Industrial Electronics, 2001,48(6): 1238-1247.

[15] Liu X, Hui S Y. Optimal design of a hybrid winding structure for planar contactless battery charging platform[J]. IEEE Transactions on Power Electronics, 2008,23(1): 455-463.

[16] Hui S Y R, Ho W W C. A new generation of universal contactless battery charging platform for portable consumer electronic equipment[J]. IEEE Transactions on Power Electronics, 2005, 20(3): 620-627.

[17] Wang C S, Covic G A, Stielau O H. Power transfer capability and bifurcation phenomena of loosely coupled inductive power transfer systems[J]. IEEE Transactions on Industrial Electronics, 2004, 51(1): 148-157.

[18] Valtchev S, Borges B, Brandisky K, et al. Resonant contactless energy transfer with improved efficiency[J]. IEEE Transactions on Power Electronics, 2009,24(3): 685-699.

[19] Liu X, Ng W M, Lee C K, et al. Optimal operation of contactless transformers with resonance in secondary circuits[C]. Twenty-Third Annual IEEE Applied Power Electronics Conference and Exposition, APEC 2008,2008: 645-650.