一种提高中频逆变器外特性的谐振控制器建模与带宽设计

陈轶涵 龚春英 邓 翔

（南京航空航天大学江苏省新能源发电与电能变换重点实验室 南京 210016）

1 引言

为了给机载交流负载供电，需要研发具备电气隔离能力的航空静止变流器将 360～800Hz的宽变频交流电和270V高压直流电变换为稳定的400Hz/115V恒频交流电为交流负载供电[1,2]。该类型的中大功率ASI系统直直变换器通常采用能够实现电气隔离的高频 DC-DC变换器得到稳定的直流母线电压，后级采用逆变器获得恒频交流电。因此后级负载逆变器的设计直接关系到 ASI系统整机的稳定性、可靠性以及输出波形的质量。

三相四桥臂逆变器拓扑三相解耦控制，通过添加第四桥臂为三相零序电流提供了通路，具备带不平衡负载能力。同时文献[3,4]通过三次谐波注入方法提高直流电压利用率，降低主功率管的电压应力，减小损耗。基于上述优势，三相四桥臂广泛应用于航空电源系统作为ASI的逆变级。

文献[5,6]证明当逆变器功率提高时，传统双环控制系统中电压调节器和电流调节器的增益有限，因此系统稳压精度往往不够高导致随着负载增加输出电压值低于额定输出电压。外特性是衡量逆变器性能的重要指标[7]。文献[8]采用了一种负载电流补偿的方法提高逆变器外特性。但是该方法引入了负载电流反馈信号，当正反馈信号大于电感电流负反馈信号时，电流环将变成正反馈，从而影响逆变器的稳定性，同时负载电流的反馈增加控制电路的复杂性。文献[9]提出了一种在控制环路中添加谐振控制器的方法，通过提高基波频率处增益的方式提高系统的稳压精度，在不影响系统的动态性能和效率的情况下改善了系统的外特性，但是该文献并未考虑谐振控制器应用于中频逆变器时，因为基波频率与系统的截止频率往往比较接近，谐振控制器在基波频率附近会造成相频曲线相位的超前和滞后，影响相频曲线低频段和截止频率处的相位造成系统稳定性问题。本文在建立中频三相四桥臂逆变器小信号模型的基础上，分析谐振控制器的引入对变换器稳定性的影响，提出一套匹配主电路与环路参数的谐振控制器设计依据。

2 中频三相四桥臂逆变器的解耦

三相四桥臂逆变器拓扑在三相三桥臂逆变器的基础上增加了一个桥臂，此时第四桥臂为零序电流提供通路，实现了带不平衡负载的能力[10]。同时第四桥臂的引入能够方便的实现三次谐波注入提高逆变器的直流电压利用率。三相四桥臂逆变器拓扑结构如图1所示。

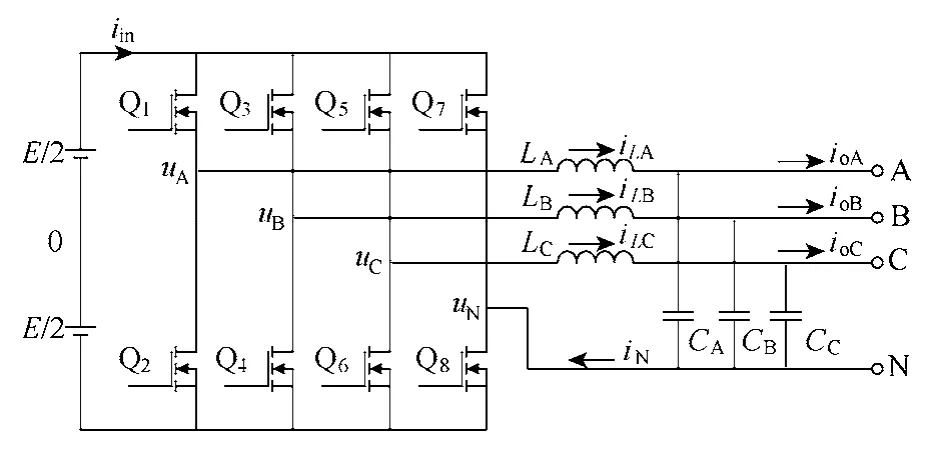
图1 三相四桥臂逆变器拓扑Fig.1 Topology of three phase four bridge

文献[10]采用平均开关状态法得到式（1）所示三相四桥臂逆变器周期平均状态模型。

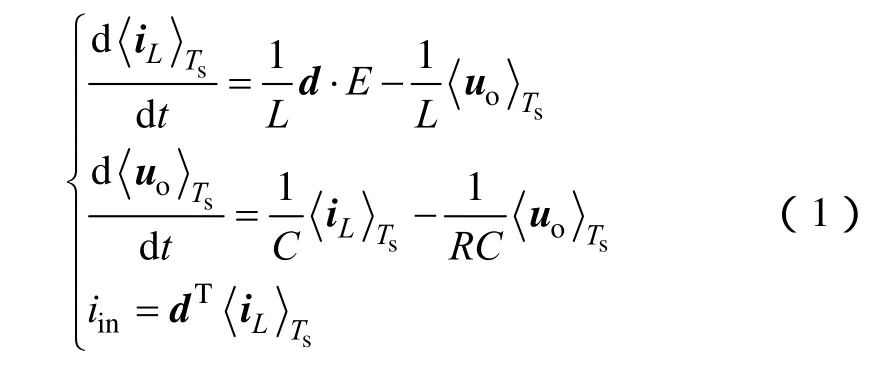
根据式（1）可以得到三相四桥臂逆变器的开关周期平均模型等效电路如图2所示。通过开关周期平均模型，能够等效三相四桥臂电路的每一相都是独立的，相互之间不存在耦合关系，可以把三相四桥臂逆变器解耦为三个独立工作的全桥逆变器，三个逆变器输出电压相位互差 120°。因此对三相四桥臂逆变器的小信号建模，可以分解为对独立的单相全桥电路进行建模和分析。

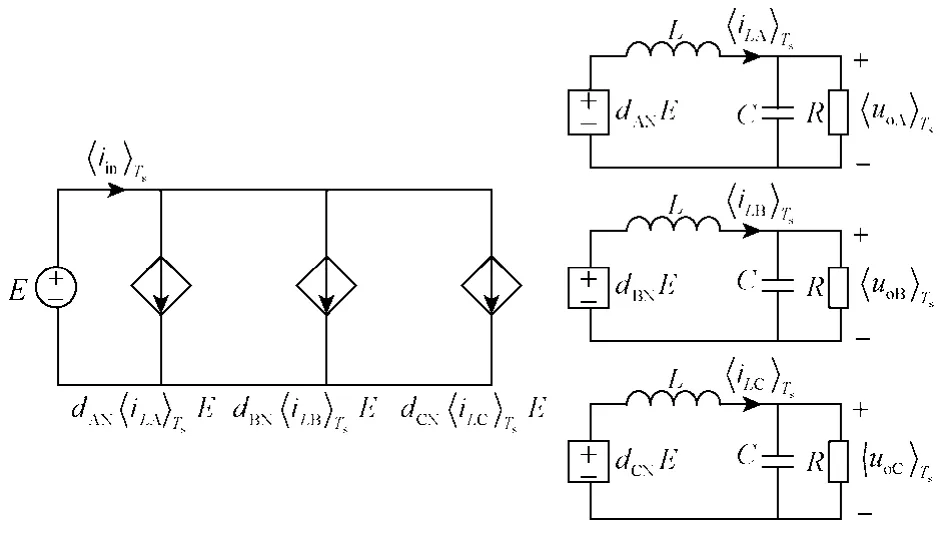
图2 三相四桥臂逆变器的开关周期平均模型等效电路Fig.2 Equivalent circuit diagram of three phase and four bridge switch cycle average model

3 控制策略及其建模

根据电力电子变换器的最优控制理论，实现全状态反馈的系统可以实现动态响应的误差平方积分指标最小，其为最优控制系统[11,12]。在开关调节系统中提取输出电压和电感电流两种反馈信号实现双环控制符合最优控制规律[13]。以A相为例，双环控制的原理框图如图 3所示，图中Vao为该相输出电压反馈值；Vrefa为输出电压正弦波基准信号；GND为控制地；Iaref为电压外环输出信号，作为该相电感电流给定；ILfa为 A相电感电流反馈值；Sa为调制信号与载波进行SPWM调制以生成控制脉冲。

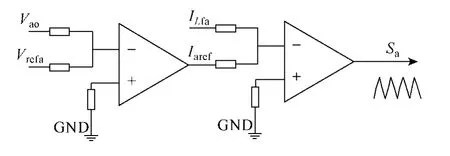
图3 双环控制原理图Fig.3 Schematic diagram of double loop control

三相四桥臂逆变器每相双环控制系统的小信号模型框图如图4所示。

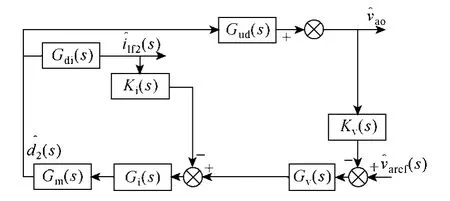
图4 三相四桥臂逆变器控制框图Fig.4 Control block diagram of three phase and four bridge

定义图 4电压电流双环控制框图中占空比-输出电压传递函数Gud(s)、占空比-输出电感电流传递函数Gdi(s)、电流内环开环传递函数Ti(s)、双环开环传递函数Tv(s)、电流环采样系数Ki(s)，电流环补偿网络传递函数Gi(s)，控制信号-占空比PWM调制传递函数Gm(s)，输出电压采样系数Kv(s)，电压环补偿网络传递函数Gv(s)。电流环补偿前后开环传递函数如式（2）、式（3）所示。

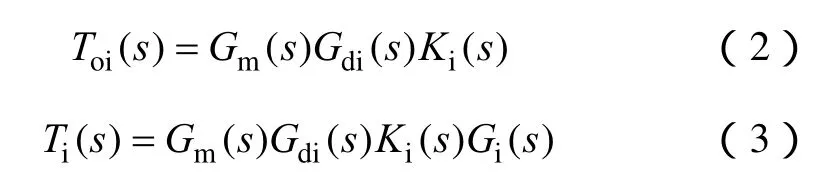
占空比与输出电感电流传递函数

式中，E为输入直流母线电压幅值；L为输出滤波电感值。

假设GR为输出滤波电感电流小信号扰动对输出电压小信号扰动的传递函数，Resr为输出滤波电容等效寄生电阻。则输出滤波电感电流对输出电压的传递函数

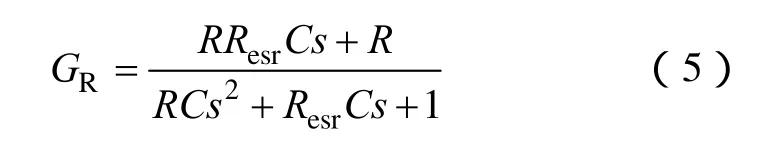
根据式（4）、式（5）可以得到占空比对输出电压的传递函数

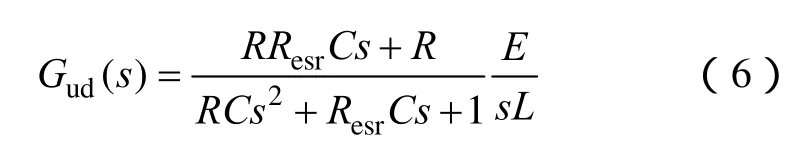
逆变器控制策略的控制性能主要体现在稳定性、动态性与抗扰性三方面。根据线性系统控制理论，系统稳定性主要反映在相角裕度和幅值裕度上。通常相位裕度大于45°，幅值裕度大于 6dB[14]。动态性能则主要体现在系统开环截止频率上，截止频率越大，动态响应越快，但是截止频率同时受到开关频率的限制，以消除系统中由开关引起的高频成分。对于采用电压电流双环控制的逆变器而言，电压环截止频率往往远远小于电流环截止频率，以获得良好的动态特性。

为了使电流补偿网络的输出反映电感电流基波分量的变化，需要对检测到的电流进行低通滤波，以消除电感电流上的高频成分，避免调制信号和载波信号的多次交割，同时使电感电流采样信号能很好地跟踪基准信号。因此希望补偿网络在低频段有很大的增益，在中频段，补偿网络的相频特性应有一个最大为 90°的超前相位，确保系统的稳定和快速的动态响应。在补偿网络的高频段放大倍数应足够小，以抑制开关频率及寄生参数引起的高频干扰及振荡。所以采用如图5所示单极点-单零点控制器作为电流环与电压环的补偿网络。对于本文中所研究的积分型控制对象，单极点-单零点补偿网络可以满足：①在穿越频率处保证足够的相位裕量；②在截止频率至开关频率范围，保证幅频特性有一个平坦的特性。

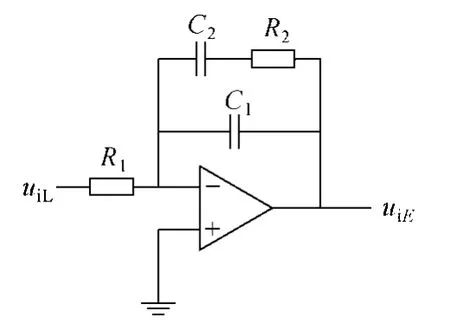
图5 电压环与电流环补偿网络Fig.5 Compensating network of voltage and current loop

式（7）为该补偿网络传递函数。补偿网络的直流增益Ki=R2/R1，零点角频率为ωzi=1 /R2C2，极点角频率ωpi=1 /R2C1

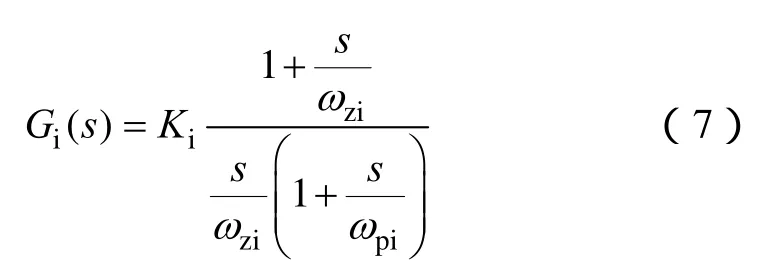
由于电流内环需要良好的动态特性，以期跟踪电压外环的输出，因此电流内环需要较大的带宽。结合式（2）～式（7），得到电流内环补偿前后的传递函数Toi(s)与Ti(s)。利用Matlab软件仿真绘制伯德图曲线验证设计结果的正确性。仿真参数根据实验室搭建的6kV·A航空静止变流器样机进行设置。输入电压为290V，开关频率20kHz，输出滤波电感Lf为 240µH，输出滤波电容Cf为 20µF，电压采样系数Kv为 0.034，电流采样系数Ki为 0.4，逆变器三相输出电压为AC115V/400Hz，三相互差120°。根据式（2）电流内环开环传递函数不包含负载阻抗项，电流内环补偿前后在不同负载的幅频和相频曲线如图6所示。

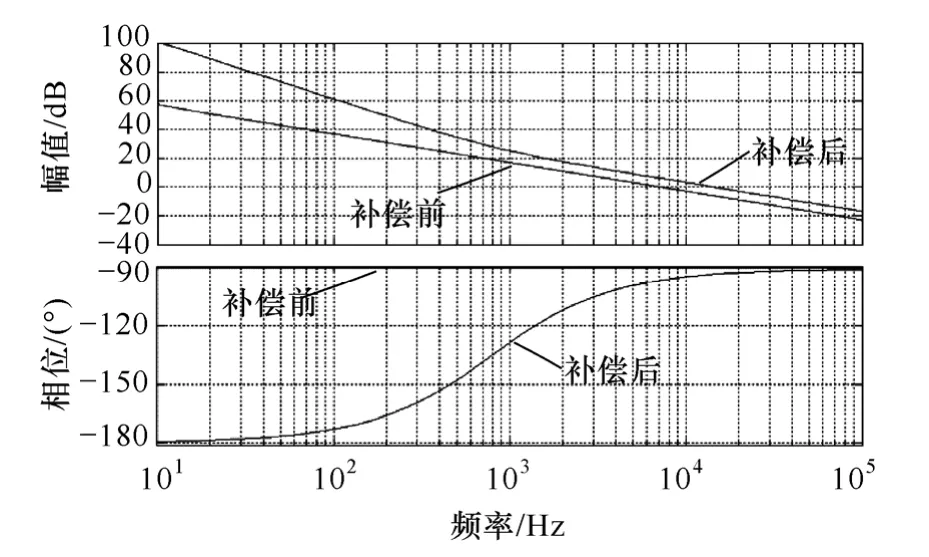
图6 电流环补偿前后伯德图Fig.6 Befor and after compensation Bode diagram of current loop

经过补偿网络Gi(s)补偿后，提高了电流环低频段的增益和截止频率。满载和空载时截止频率皆为12kHz，系统获得较好的动态性能。对于同样的补偿网络参数随着负载的降低截止频率随之降低。所设计补偿网络使电流环开环传递函数相角裕度大于 45°，幅值裕度大于 6dB，满足稳定性和动态性要求。

电压控制器的控制对象是由电流内环和负载组成的，根据图4建立的小信号模型结合式（2）～式（7），设计电压环参数，得到电压外环补偿前后的伯德图如图7所示。

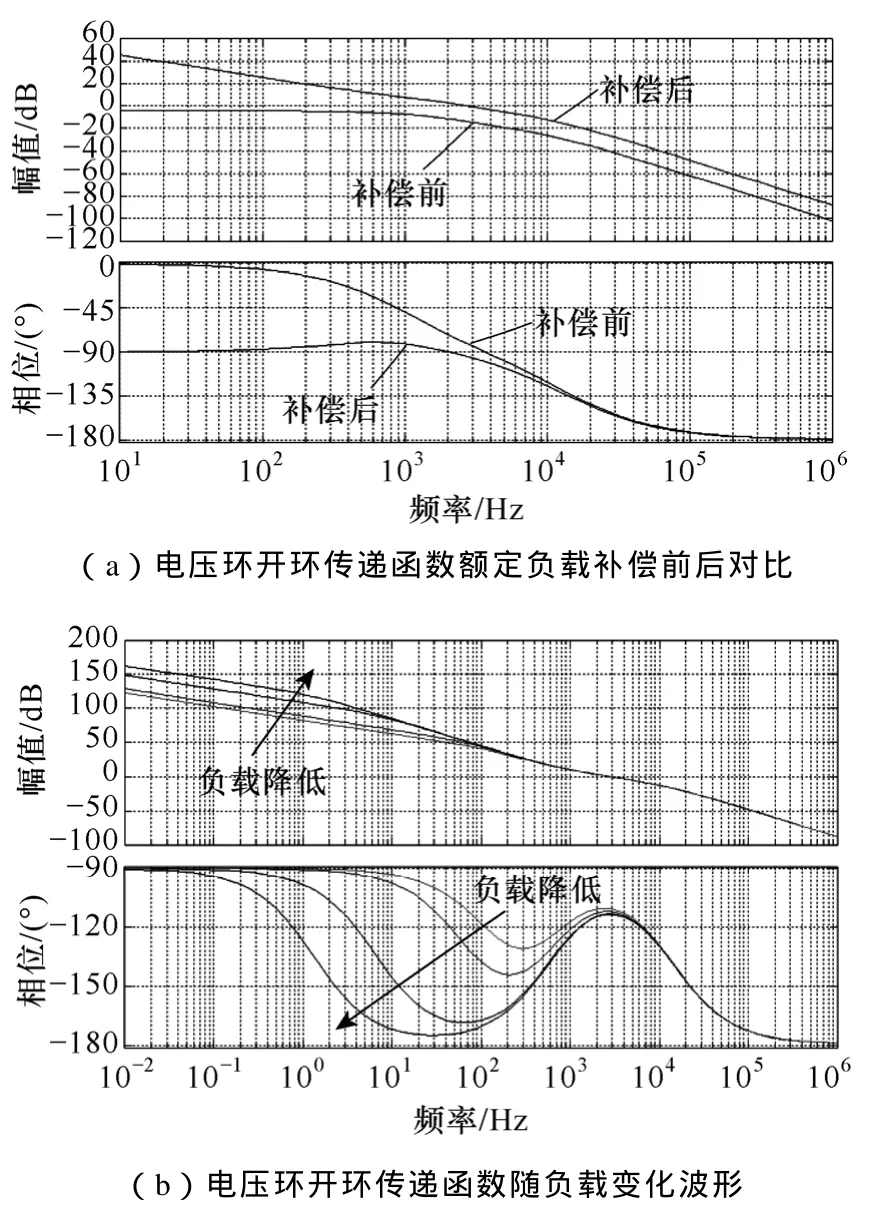
图7 无谐振控制器电压环开环传递函数伯德图Fig.7 Befor and after compensation Bode diagram of voltage loop without resonant controller

图 7a中设计电压环补偿网络将截止频率设置在1.2kHz，相位裕度大于45°，满足系统稳定性动态性要求。根据图7b所示，随着负载从额定负载到空载不断降低，低频段的相位逐渐接近-π，此时截止频率大于低频段相位偏移频率段，且截止频率处的相位裕度不发生明显的变化，对逆变器的动态特性和稳态特性不会产生影响。考虑系统实际为非理想系统，由于变换器采样、控制等环节固有的延迟特性，低频段的相位在延迟的影响下空载或轻载状态下有可能穿越-π。这就需要根据自动控制原理稳定性判据来重新定义系统的稳定性。

4 谐振控制器的建模与带宽设计

外特性指标代表了逆变器输出电压受负载的影响程度。性能优良的逆变器通常具有较硬的外特性，逆变器空载到满载过程中输出电压的幅值降低较少[15]。

文献[16]认为提高电压环电流环增益是提高逆变器外特性的一种有效策略，但是过高的增益会提升电压环和电流环的截止频率，同时提高非基波频率段的增益，会降低系统的抗扰性，对ASI系统的稳定性产生影响。

在逆变器双环控制的基础上引入谐振控制器，是一种有效提高逆变器外特性的控制策略。该方法通过提高了基波频率处的增益优化逆变器的外特性，该控制策略控制框图如图8所示。

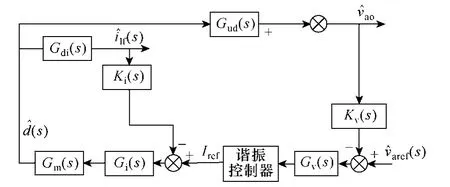
图8 包含谐振控制器的逆变器控制框图Fig.8 Control block diagram of three phase and four bridge with resonant controller

谐振控制器的传递函数为

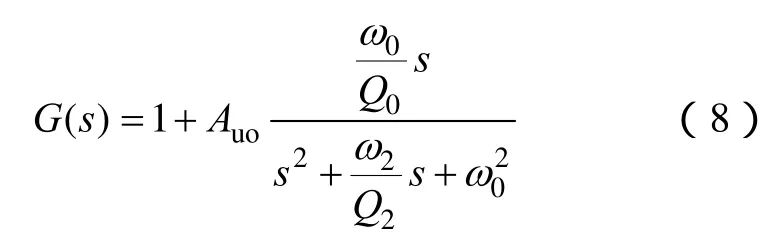
图9a所示为该谐振控制器的幅相曲线。该谐振控制器等效为带通滤波器，提高了系统开环传递函数基波频率400Hz处的增益。

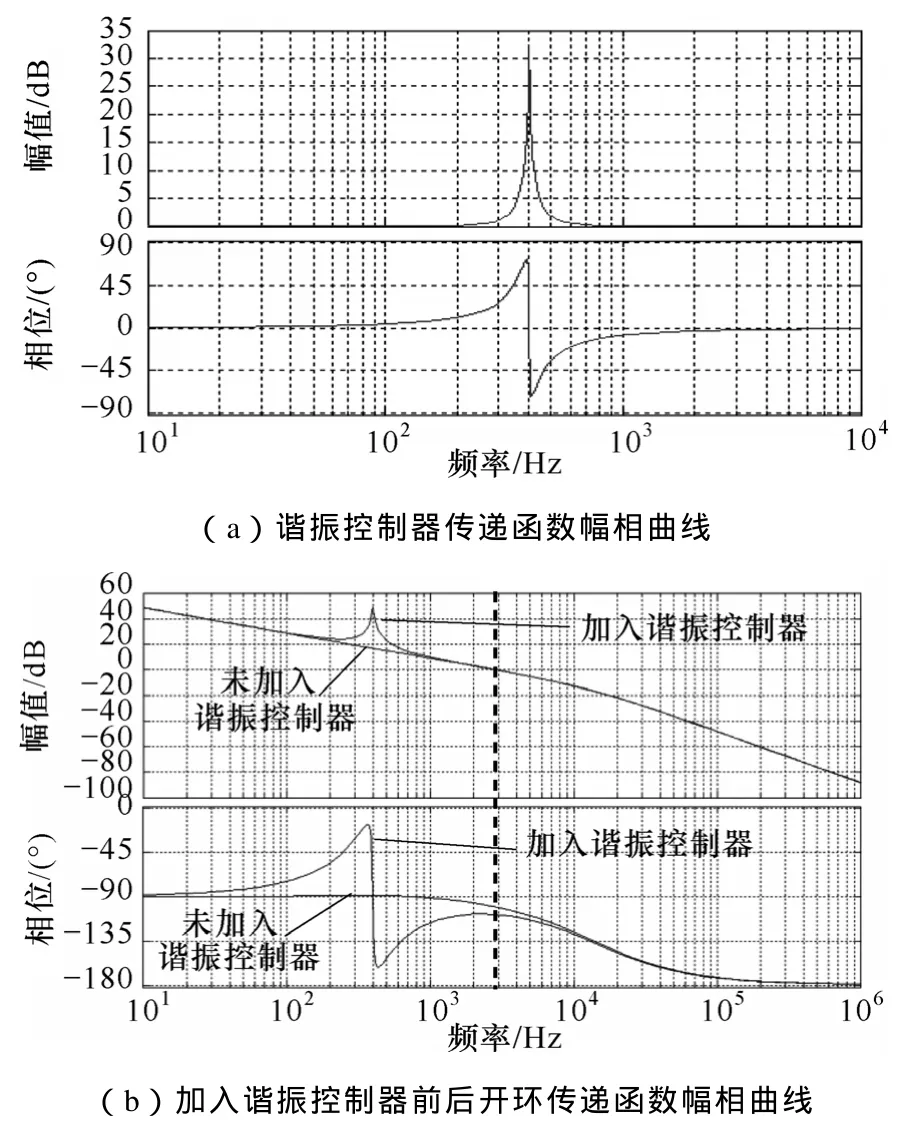
图9 谐振控制器幅相曲线Fig.9 Bode diagram of resonant controller

根据图 9a中相频特性曲线可以发现该谐振控制器会造成基波频率处相位的滞后和超前，设计补偿网络时为了提高系统的稳定性，往往将系统开环传递函数的截止频率设置在 1/20或者 1/10的开关频率处，这使得系统的截止频率非常接近基波频率，谐振控制器对相位的影响就会使截止频率处的相位裕度发生偏移，此时必须保证相位裕度大于 45°，以保证系统的稳态和动态性能。

图9b所示，谐振控制器仅在低频段（逆变器输出基波频率附近）提高环路增益，同时影响该频率段的相位，对于截止频率以及中频段没有任何影响，因此谐振控制器的加入，及其带通宽度不会降低系统的动态性能。同时，据图7b所示低频段的相位随着逆变器负载降低而减小，当谐振控制器造成在空载或轻载下相频特性曲线穿越-π，需要根据自动控制原理的稳定性判据对逆变器的稳定性重新评估。

设置谐振控制器的中心频率为 400Hz，带宽为60Hz，增益为 40dB，引入谐振控制器前后系统电压环经过补偿后开环传递函数伯德图如图10所示。根据图 10a，当在控制环路中加入谐振控制器后，轻载下低频段相位与未加入谐振控制器前比较更低，使相频特性曲线穿越-π，同时在该频率段增益大于0dB。

根据图 10b，当负载降低时，该穿越频率相位偏移深度会随之加深。根据奈氏判据[17,18]，设传递函数右半平面极点数为P，相频特性曲线正穿越-π的频率点数为N+，相频特性曲线负穿越-π的频率点数为N-，则

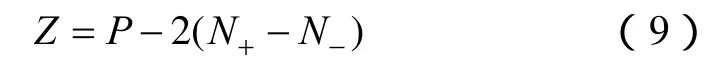
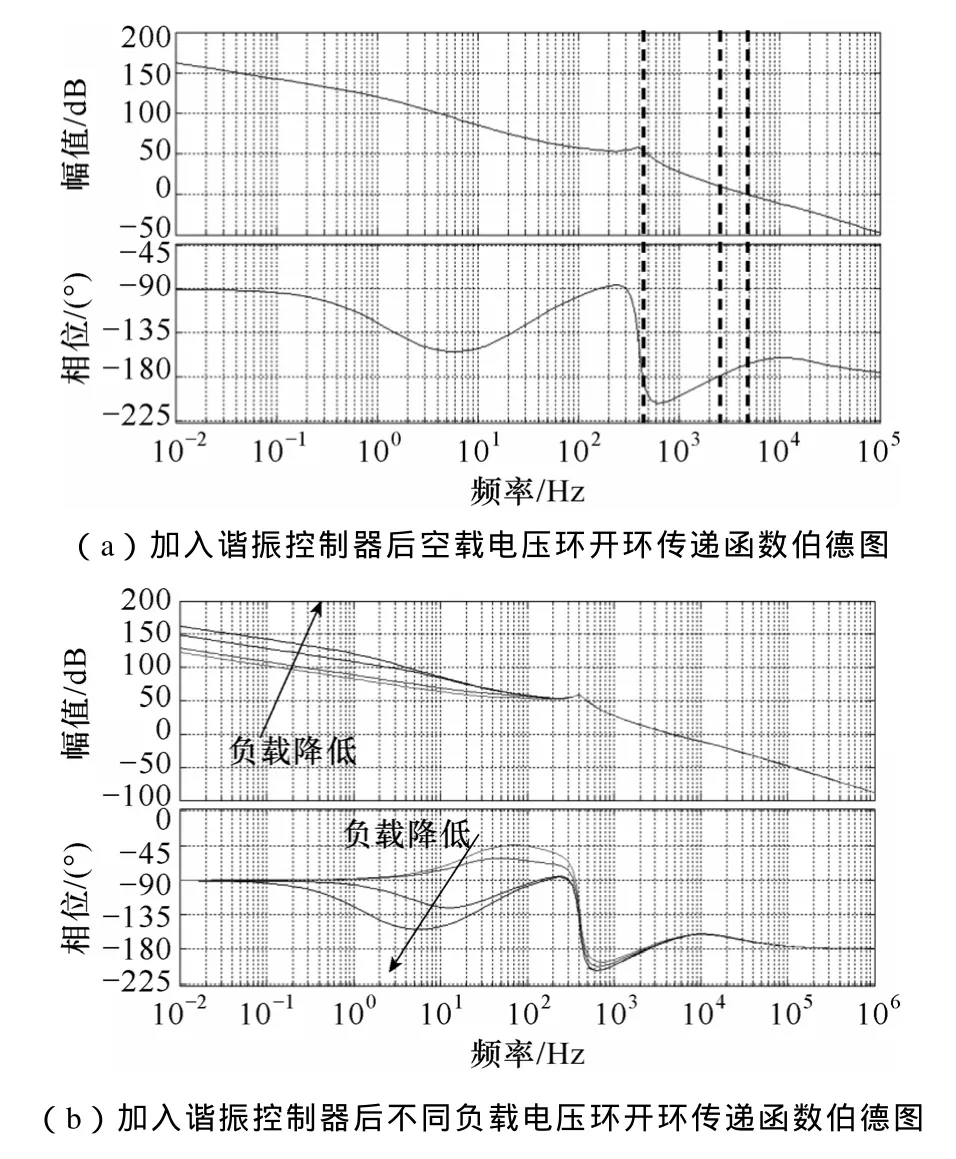
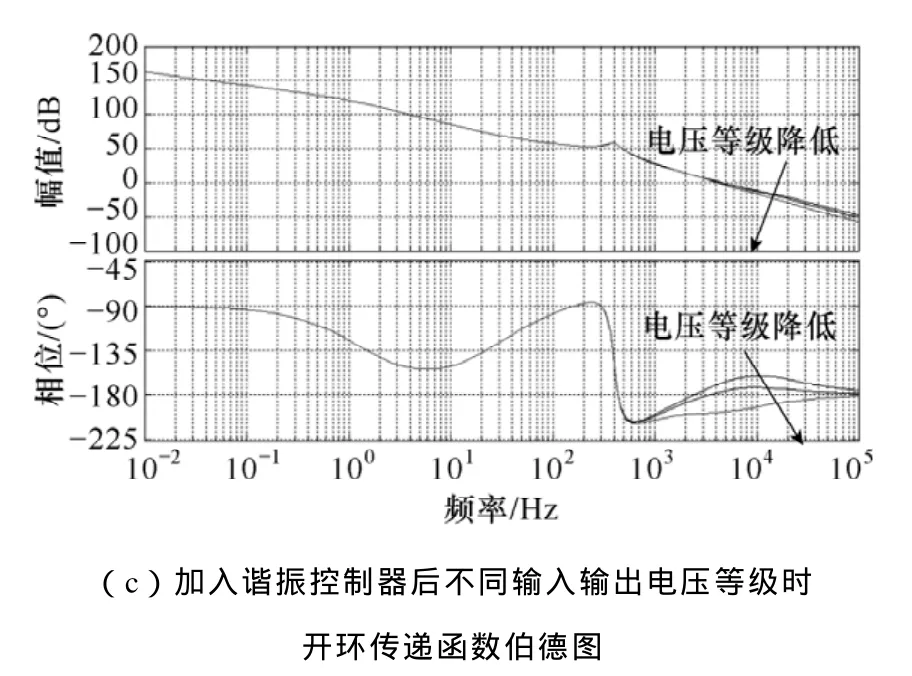
图10 谐振控制器带宽为60Hz电压环开环传递函数伯德图Fig.10 Bode diagram of voltage loop open loop transfer function when resonant controller’s bandwith is 60Hz

当Z=0时可以认为系统是稳定的。其根据图10a所示，2(N+-N-)=0 ，则需要判断式（9）中P是否为0，即Tv(s)是否含有右半平面极点。根据式（2）～式（8）并代入仿真参数计算Tv(s)的极点方程解为

极点方程解中不包含实部为正的值，即不存在右半平面的极点，则可以判断系统是稳定的。

根据图 10a，在截止频率处因为谐振控制器的影响，相位裕度低于 45°，此时虽然可以认为系统仍然是稳定的，但是考虑实际逆变器控制和主电路的非理想状态会发生延迟，进而影响截止频率处的相位裕度。当满足以下两个条件：①增益约等于 0；②增益为0处频率对应相频特性曲线相位小于-π，则满足自激振荡条件，此时系统会发生等幅恒定频率的自激振荡。

据图10c所示，当降低逆变器输入输出电压等级，会使截止频率相位随着谐振控制器的作用进一步降低，最终在空载状态下相位低于-π，此时通过奈氏判据判断系统是稳定的，但是在截止频率处出现相位低于-π的正反馈，满足自激振荡的两个约束条件，因而逆变器的输出电压会出现自激振荡现象。

因此若降低谐振控制器的带宽，能够有效减小谐振控制器基波频率附近相移频率段的宽度。重新设计谐振控制器带宽为5Hz，增益保持40dB，获得电压环开环传递函数伯德图如图11所示。

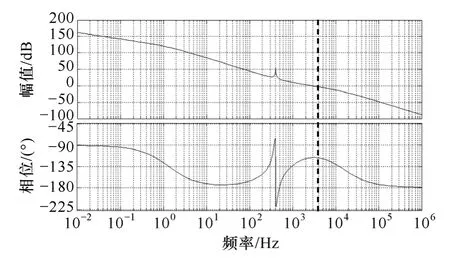
图11 谐振控制器带宽为5Hz电压环开环传递函数伯德图Fig.11 Bode diagram of voltage loop open loop transfer function when resonant controller’s bandwith is 5Hz

降低谐振控制器带宽后，谐振控制器相移范围变窄，将不会对截止频率处相位裕度产生作用影响系统的稳定性，同时空载和轻载下低频段-π的穿越依然存在，需要通过求解电压环开环传递函数极点方程，重新根据其是否包含右半平面极点判断系统的稳定性。

5 仿真和实验验证

设计谐振控制器带宽为80Hz，通过Saber仿真软件进行逆变器仿真与 Matlab所绘制伯德图进行对比。Saber仿真主电路和控制电路参数同图10a的Matlab仿真参数相同。仿真结果如图12所示。

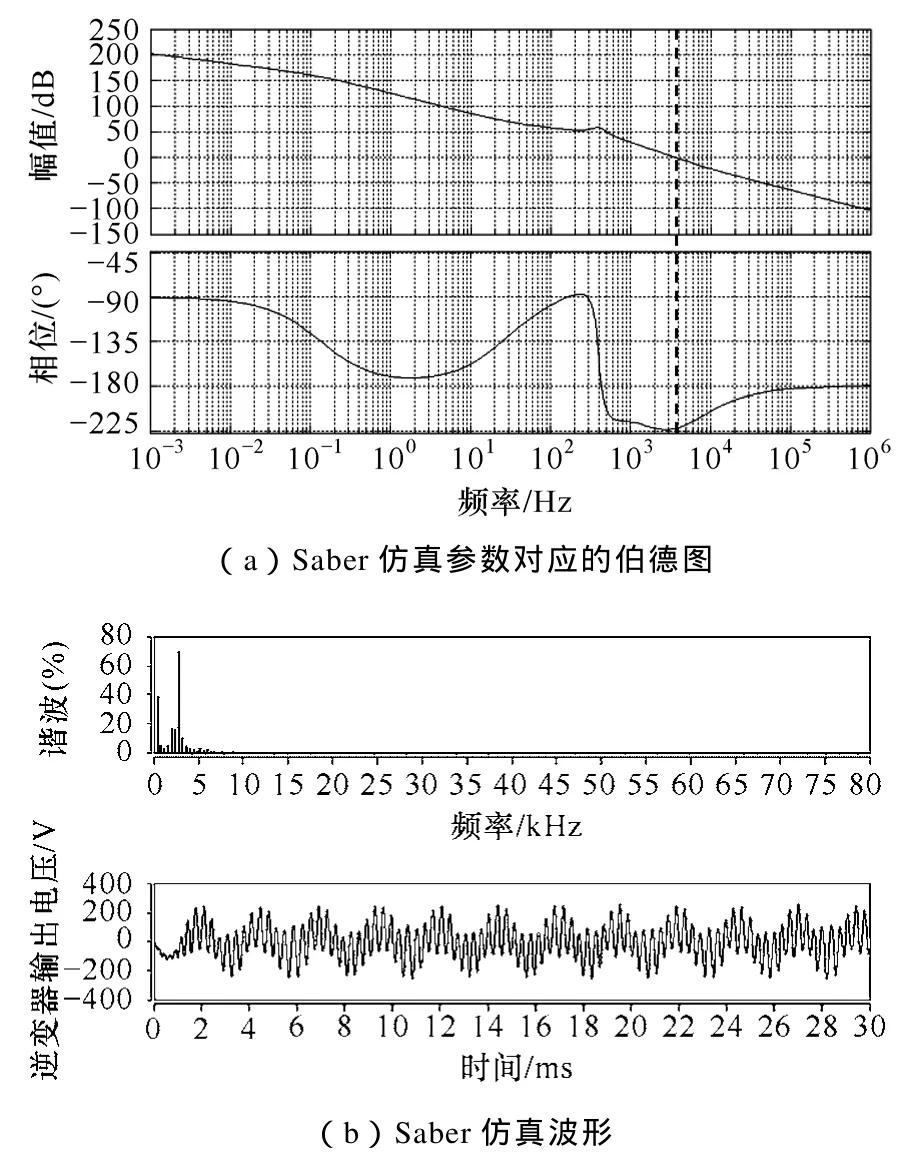
图12a表明在谐振控制器的影响下增益为0dB处截止频率为2.9kHz，对应的相位小于-π，满足自激振荡条件，此时图12b中逆变器输出电压波形在基波频率上叠加低频振荡成分，对该波形进行傅里叶分析，如图12b中谐波分布图所示，该振荡频率为2.8kHz，与伯德图自激振荡点基本吻合，证明本文对谐振控制器引起变换器自激振荡现象分析的正确性。

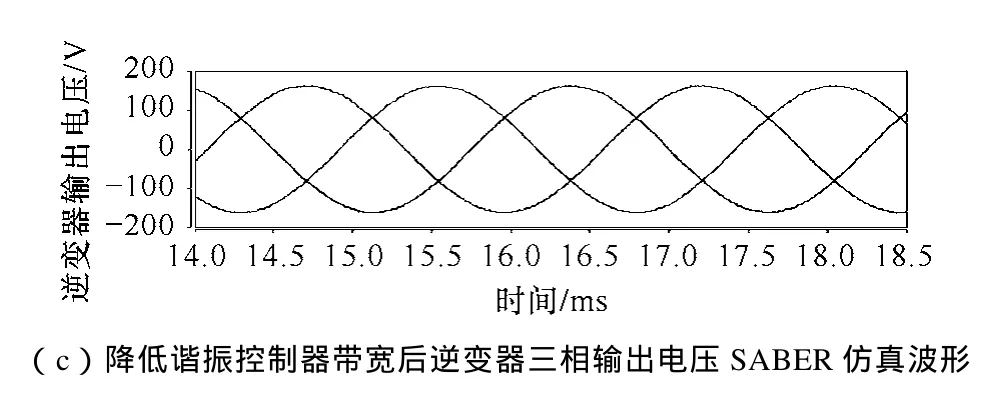
图12 SABER仿真波形与伯德图Fig.12 Waveform of Saber simulation and Bode diagram

当降低谐振控制器带宽为 5Hz，Saber仿真结果如图12c所示，因为截止频率处相位不再受谐振控制器的影响，输出电压自激振荡问题得到抑制。

为了验证本文提出的谐振控制器参数设计方案，在实验室制作一台6kV·A两级式航空静止变流器平台进行实验验证。

样机主电路拓扑和参数与Matlab以及Saber仿真参数一致。并降低谐振控制器带宽，同时根据奈氏判据设计补偿网络，使系统在空载和轻载不包含右半平面极点，得到6kV·A航空静止变流器启动与稳态工作实验波形如图13所示。

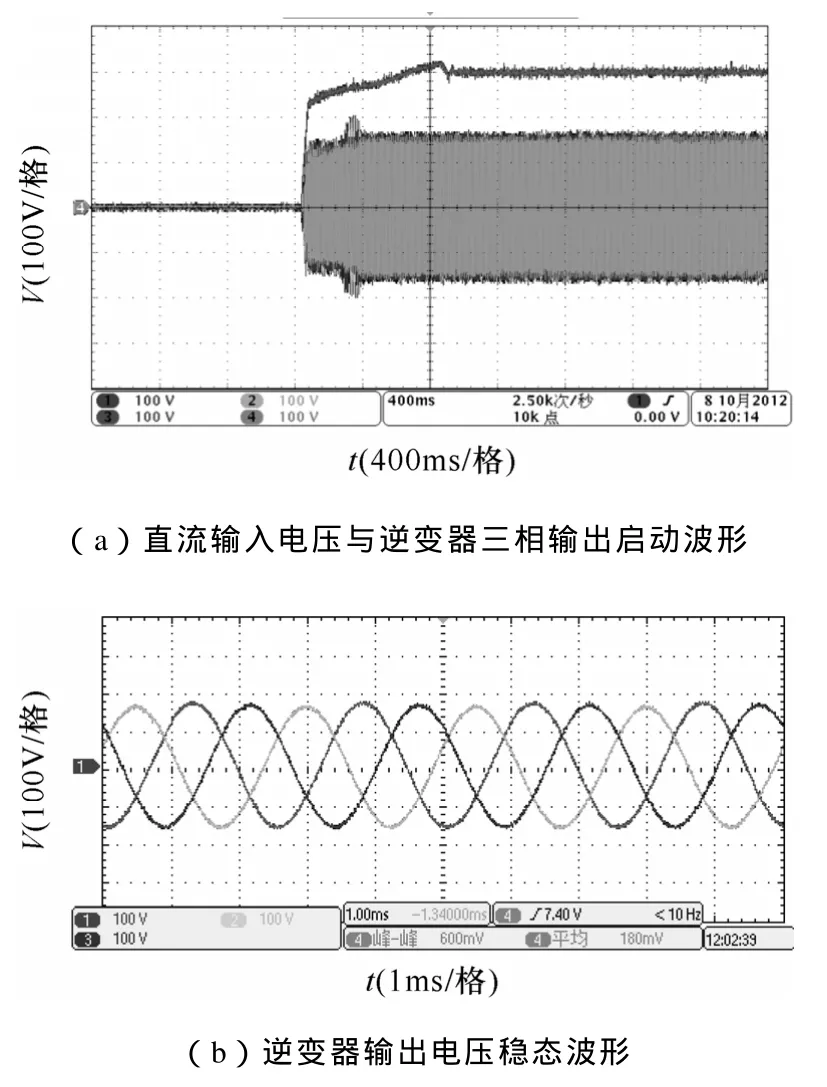
图13 直直变换器及级联后各级变换器输出电压波形Fig.13 Output voltage waveforms of the DC-DC converter and inverter

图13a中，示波器通道3为ASI前级直直变换器 300V输出直流电压建压波形，即逆变器输入直流电压启动波形；示波器通道 1、2、4、为逆变器三相输出电压启动波形。图13b为逆变器三相输出稳态实验波形。ASI启动时间约为 900ms，实验中逆变器具有良好的动态和稳态性能，证明遵循本文所提出的谐振控制器设计依据能够保证中频ASI逆变器的稳定工作。

为了进一步考验逆变器的动态性能，验证优化后的谐振控制器对逆变器的稳定性和动态性不造成影响，对实验平台进行短路实验，短路电流峰值为53A，采用A相短路对地电路方式进行实验，A相电感电流波形如图14所示。图14表明逆变器动态性能能够达到ASI对负载短路的要求。

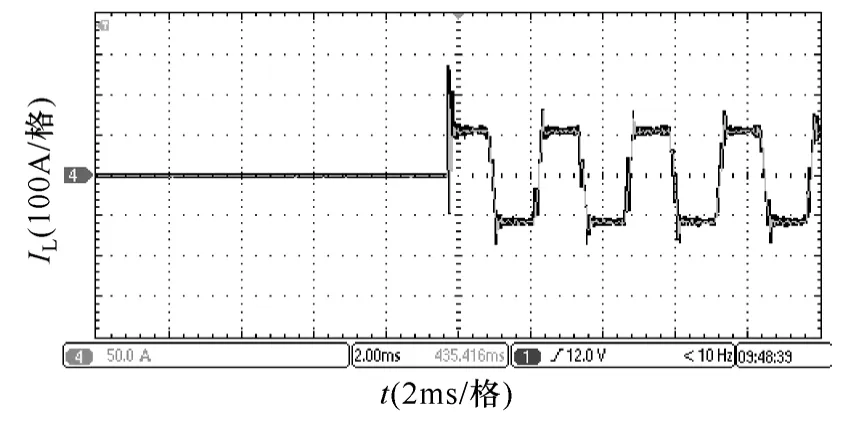
图14 一相短路电感电流波形Fig.14 Inductor current waveform of one phase shor circuit

对不同负载的逆变器三相输出电压进行实验测试，实验结果见下表。三相四桥臂逆变器在加入谐振控制器之前，输出电压随着负载从 1～6kV·A增加而降低，最终降低幅值最大值达到5V，加入谐振控制器后负载由 1～6kV·A增加输出电压降低幅值最大值为1.3V。实验证明基于本文谐振控制器优化设计依据，加入谐振控制器后的逆变器不仅动态、稳态性能能够达到设计要求，而且逆变器输出电压随着负载提高下降值减小，三相输出平衡度和稳定性得到了提高，逆变器的外特性符合测试指标要求。

表 逆变器外特性实验数据Tab. Experimental data of inverter’s External Characteristic

6 结论

本文在建立三相四桥臂逆变器全负载状态小信号模型的基础上，分析了电压电流补偿网络对逆变器稳态和动态性能的影响。为了优化逆变器外特性，采用了谐振控制器提高基波频率增益的控制策略。并通过中频 ASI逆变器中谐振控制器的小信号建模，论证了在轻载或空载状态下，谐振控制器造成逆变器开环传递函数相频特性曲线低频段穿越-π。证明了当谐振控制器带宽设计过宽将降低系统相位裕度造成自激振荡。最后本文提出了一套适用于中频逆变器的谐振控制器优化设计依据，给出了轻载、空载状态稳定性判断标准，通过仿真和实验验证了分析结果的正确性，得到以下结论：

（1）谐振控制器等效于带通滤波器，通过提高基波频率处的增益提高逆变器外特性，其对截止频率点没有影响，但是会造成基波频率附近频段的相移，进而影响相位裕度。

（2）随着逆变器负载的降低，在小于基波频率的低频段相位会随之接近-π，在谐振控制器作用下，相频特性正负穿越-π各一次，需要通过解开环传递函数极点方程的方法重新判断系统在空载和轻载下的稳定性。

（3）谐振控制器带宽过宽会造成中频逆变器截止频率处相位裕度降低，当穿越频率处相位低于-π，同时根据极点方程判断系统又是稳定时，逆变器输出将出现自激振荡现象，在基波频率上叠加N倍基波频率的谐波，该谐波频率接近截止频率。同时谐振控制器对逆变器截止频率处正反馈深度随着逆变器输入输出电压等级成反比，而且该正反馈不会随着负载的提高而减弱。因此需要尽可能缩小用于提高中频逆变器外特性的谐振控制器带宽以降低谐振控制器对环路稳定性的影响。

[1] Faleiro L. Initial research towards a more electrical aircraft[C]. More Electrical Aircraft Conference Royal Aeronautics Society,2004: 245-257.

[2] Lester Faleiro. Beyond the more electrical aircraft[J].Aero Space America,2005(9): 261-273.

[3] 姚凯,阮新波,冒小晶,等. 减小 DCM Boost PFC变换器储能电容的方法[J]. 电工技术学报,2012,27(1): 172-181.

Yao Kai,Ruan Xinbo,Mao Xiaojing,et al. A method of reducing storage capacitor of DCM Boost PFC converter[J]. Transations of China Electrotichnical Society,2012,27(1): 172-181.

[4] 杨宏. 四桥臂三相逆变器的控制和实现[D]. 南京:南京航空航天大学,2004.

[5] 张卫平. 开关变换器的建模与控制[M]. 北京: 中国电力出版社,2005.

[6] 阚加荣,吴云亚,谢少军. 控制参数对并联逆变器性能的影响[J]. 电工技术学报,2009,24(9): 120-126.

Kan Jiarong,Wu Yunya,Xie Shaojun. Design of control parameters for parallel-connected inverters[J].Transactions of China Electrotechnical Society,2009,24(9): 120-126.

[7] 中华人民共和国国家军用标准GJB 181A—2003[S].中国: 2003.

[8] 李正兴. 6kV·A单相中频逆变器的研制[D]. 南京:南京航空航天大学,2007.

[9] 马海啸,陈凯,龚春英. 双 buck逆变器的建模与优化设计[J]. 电工技术学报,2012,27(8): 35-41.

Ma Haixiao,Chen Kai,Gong Chunyin. Modeling and optimization design of dual-buck inverter[J]. Transactions of China Electrotechnical Society,2012,27(8):35-41.

[10] 孙驰,鲁军勇,马伟明. 一种新的三相四桥臂逆变器的控制方法[J]. 电工技术学报,2007,22(2): 67-73.

Sun Chi,Lu Junyong,Ma Weiming. A novel control method for three-phase four-leg inverter[J]. Transactions of China Electrotichnical Society,2007,22(2): 67-73.

[11] 蔡宣三,龚绍文. 高频功率电子学直流-直流变换部分[M]. 北京: 科学出版社,1993.

[12] Mahapatra,K K,Ghosh A. Doradla S R. Simplified model for control design of STA using three-level inverter[C]. 34th Annual Conference of the IEEE Industrial Electronics Society,2008: 536-539.

[13] 黄如海,谢少军. 基于比例谐振调节器的逆变器双环控制策略研究[J]. 电工技术学报,2012,27(2):77-81.

Huang Ruhai,Xie Shaojun. Double-loop digital control strategy based on proportional-resonant controller[J].Transactions of China Electrotechnical Society,2012,27(2): 77-81.

[14] 储仁杰,贲洪奇,吴辉. FB-ZVZCS变换器小信号建模及补偿器设计[J]. 控制工程,2008,15(3): 302-309.

Chu Renjie,Ben Hongqi,Wu Hui. Small-signal modeling of FB-ZVZCS converter and compensator design[J].Control Engineering of China,2008,15(3): 302-309.

[15] 孙驰,马伟明,鲁军勇. 三相逆变器输出电压不平衡的产生机理分析及其矫正[J]. 中国电机工程学报,2006,26(21): 57-64.

Sun Chi,Ma Weiming,Lu Junyong. Analysis of the unsymmetrical output voltage distortion mechanism of three-phase inverter and its corrections[J]. Proceedings of the CSEE,2006,26(21): 57-64.

[16] 官二勇,宋平岗,叶满园. 基于三次谐波注入法的三相四桥臂逆变电源[J]. 电工技术学报,2005,20(12): 43-52.

Guan Eryong,Song Pinggang. Ye Manyuan,Threephase inverter with four bridge legs based on three harmonic injection method[J]. Transactions of China Electrotechnical Society,2005,20(12): 43-52.

[17] 张欣,阮新波. 用于提高级联型电源系统稳定性的自适应有源电容变换器[J]. 电工技术学报,2012,27(2): 23-32.

Zhang Xin,Ruan Xinbo. Adaptive active capacitor converter for improving the stability of cascaded DC power supply system[J]. Transactions of China Electrotechnical Society,2012,27(2): 23-32.

[18] 胡寿松. 自动控制原理[M]. 北京: 科学出版社,2007.