电力系统扩展黑启动方案动态综合评估

顾雪平 王大江 梁海平 刘 艳

（华北电力大学新能源电力系统国家重点实验室 保定 071003）

1 引言

智能电网是世界电力工业的共同发展趋势[1]，建设智能电网将使未来电网更加安全可靠，但其安全稳定运行仍然受到外部环境因素和内部技术问题的影响，灾难性事故仍无法完全避免，世界范围内影响人口最多的印度2012年“7.30”、“7.31”大停电事故再次敲响了警钟[2]。科学合理的恢复方案是应对大停电事故的有效预案，对事故后的有序恢复起到重要作用，扩展黑启动策略的提出为恢复控制提供了一种新思路[3]，相比于起动一台机组的常规黑启动方式，扩展黑启动策略能够为后续恢复提供更多功率，加快恢复进程，因此，对扩展黑启动方案评估优选具有重要意义。

黑启动方案评估排序是黑启动问题研究的重要内容之一，众多专家学者将多种评估决策理论引入到该研究中，作出了大量有益的探索，取得了一些卓有成效的成果，主要的评估方法包括数据包络分析模型及与其他方法相结合的改进模型[4-6]、模糊评估方法[7-11]、群体决策理论[12-14]、熵权决策方法[15]、Vague集理论[16]、主成分分析法[17]几类，但现有研究多数停留在静态评估层面，只利用黑启动阶段的评价值进行方案评估排序，未将方案对后续恢复的影响纳入到评估结果中，而大停电后的恢复过程是一个连续的动态过程，黑启动阶段是恢复的初始阶段，所形成的局部网络是后续恢复的基础，不同的方案对后续恢复影响不同，方案的评价不仅要看黑启动阶段的恢复状况，还要考虑对后续恢复过程的影响而进行综合评估，选择在黑启动阶段和后续恢复阶段整体上最优的方案。

本文在对现有黑启动方案评估及动态综合评估理论学习借鉴的基础上[18-21]，以时序动态视角对扩展黑启动方案进行动态综合评估。首先提出了动态评估的框架，将时间维度划分为黑启动阶段和后续恢复阶段两个时段，构建了两个时段的评估指标，采用组合赋权法得到指标的综合权重，以线性加权模型对各时段指标集结得到待评估方案不同时段的评价值。在此基础上，求解基于“时间度”概念的非线性熵值规划法确定黑启动阶段和后续恢复阶段的最优时间权重，以时序加权平均算子和时序几何平均算子组成的混合算子模型对两时段评价值再次集结，得到方案所有时段的最终综合评估结果。

2 扩展黑启动方案动态综合评估框架及指标体系

2.1 方案动态综合评估框架

静态评估主要用于解决由指标集、方案集构成的二维空间决策问题，动态评估是在二维决策空间的基础上还要考虑时间维度的三维空间决策问题，评估数据由平面数据演变为具有时间标度的时序立体数据。本文尝试从方案集、指标集、时间集三个维度对扩展黑启动方案进行动态综合评估。为使其综合评估结果包含黑启动阶段的恢复结果和对后续恢复的影响，本文借鉴现有系统恢复研究中将恢复过程分阶段考虑的方式，将恢复过程时间维度划分为黑启动恢复阶段、后续恢复阶段两个时段，即从当前和将来发展趋势两部分进行动态综合评估，使评估结果更全面科学，评估框架如图1所示。对扩展黑启动方案实施动态综合评估，决策者既能从宏观整体上掌握方案的总体评估结果，又能了解到恢复过程中不同阶段的动态恢复状况，为综合决策提供多角度的参考依据。由于主网架建立后的全面负荷恢复阶段目标较单一，本文的后续恢复指后续的网架重构，对于后续网架重构，以待评估方案在黑启动阶段形成的局部网络为基础，采用文献[22]提出的“分时步、整体寻优”策略，即从网架重构整体最优的角度优化出每一时步恢复的机组和负荷进而完成后续恢复。

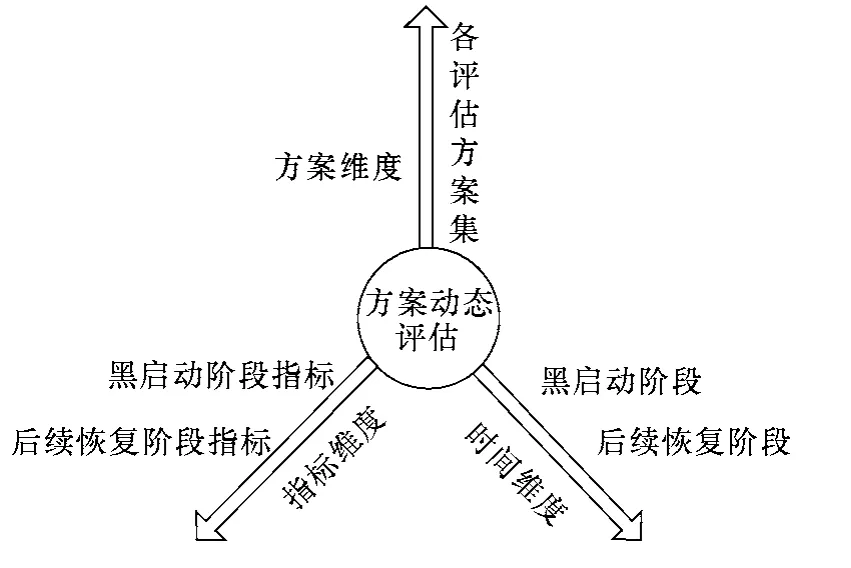
图1 扩展黑启动方案动态评估框架Fig.1 Dynamic assessment framework of extend-black schmes

2.2 评估指标体系

评估指标从不同方面反映了系统恢复各阶段的多种因素，遵循指标制定的科学性、系统性、实用性等基本准则，结合系统恢复的具体实际，参考已有研究成果，从黑启动阶段和后续恢复阶段两个时段实际特点分别提炼各自的指标，构建适用于扩展黑启动方案动态评估的指标体系，见表1。

表1 评估指标体系Tab.1 The assessment index system

表1中部分指标定义如下：

（1）路径指标I1反映了黑启动阶段被启动机组恢复路径的状况，将路径指标I1定义为

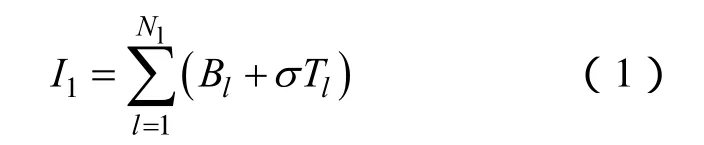
式中，Nl为黑启动阶段恢复的线路数；Bl为线路l折算到同一电压等级下的电纳；Tl为线路l是否经过电压等级变换，是为1，否为0；σ为转换系数。

（2）技术指标I4包括充电路径过电压、黑启动电源自励磁、电压稳定和频率稳定四个单项校验指标，各单项指标计算准则见文献[4]，其中电压稳定与频率稳定指标分别取启动的多台机组中电压下降最大、频率跌落最大值为本方案指标值。以所有待评估方案中各单项指标最优值为基准进行归一化，由归一化后的各单项指标叠加组成技术指标I4。

（3）黑启动阶段启动的机组不仅是黑启动阶段恢复效果的体现，也影响后续恢复，综合考虑机组性能、位置重要度因素，将机组恢复指标I5定义为

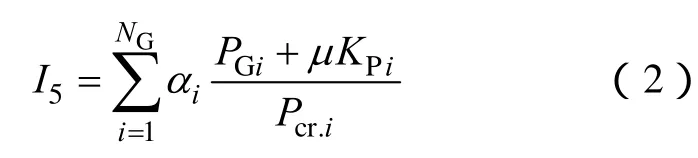
式中，NG为恢复的小系统中机组个数；αi为机组i所在节点的重要度，以节点收缩后的网络凝聚度表示[23]；PGi为机组i的额定功率；KPi为机组i的爬坡速率；cr.iP为机组i的启动功率；μ为转换系数。

（4）启动功率指标I7反映了后续恢复对启动功率的需求，以后续恢复各时步需要的启动功率加权和表示为

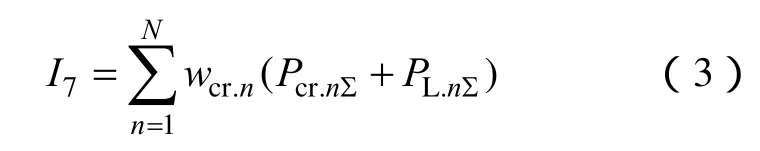
式中，N为后续恢复时步总数；Pcr.nΣ为第n时步恢复的机组启动功率之和；PL.nΣ为n时步恢复的负荷总量；wcr.n为n时步启动功率的权值。

（5）路径指标I8反映了后续恢复阶段机组和负荷恢复的恢复路径状况，计算公式为

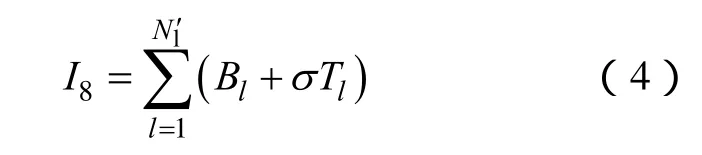
式中，N'l为后续恢复阶段恢复的线路数。

（6）定义恢复机组容量指标表征后续恢复阶段机组的恢复效果，以后续恢复各时步恢复的机组容量加权和表示。即

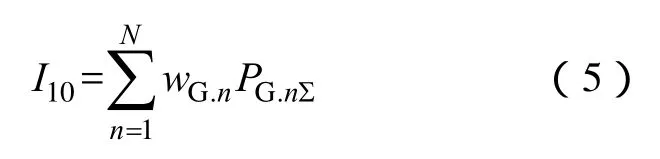
式中，wG.n为n时步启动的机组容量权值；PG.nΣ为n时步恢复的机组额定容量和。

（7）恢复负荷量指标I11体现了后续恢复中负荷恢复的成果，以各时步恢复的负荷量加权和表示，即

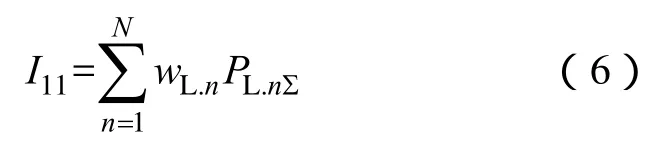
式中，wL.n为时步n恢复负荷的权值；PL.nΣ为时步n恢复的负荷量。

（8）定义骨架网络度指标衡量最终形成的网架结构重要性，从复杂网络拓扑特性角度研究最终形成的目标网架骨架网络度，将其定义为

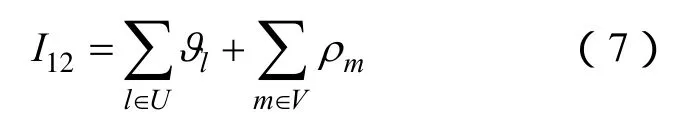
式中，U为最终恢复的目标网架所有线路集合；lϑ为线路l的重要度，以其介数表示[23]；V为最终恢复的目标网架所有节点集合；mρ为节点m的重要度。

3 基于线性加权模型的方案各时段静态评估

3.1 指标标准化处理

将恢复过程时间集表示为ψ=｛t1,t2｝（t1表示黑启动阶段，t2表示后续恢复阶段），待评估的方案集为S=｛s1,s2,…,sn｝ ，不 同 时 段 的 指 标 集 为I(tk)=｛I1(tk),I2(tk),…,Im(tk)｝（k=1,2），方案si(i=1,…,n)在tk时段的第j(j=1,…,m)个指标值为(tk)，由S中所有方案不同时段全部指标(tk)｝构成的时序立体数据表表示为(tk)｝，(tk)｝中各指标量纲不完全相同，不便于分析比较，影响到评价结果的合理性，为使指标数据间具有可比性，需进行标准化处理。本文采用极差化标准化方法，该方法对原始指标数据的数量及分布无要求，采用线性化方法对原始指标数据标准化处理，标准化后的指标数据与原始指标数据保持较高一致性，利于下一步评估，具体标准化步骤如下。

收益型指标标准化公式为

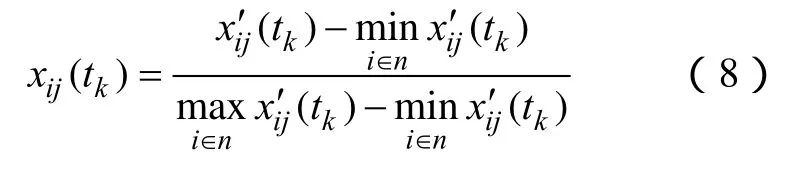
成本型指标标准化公式为

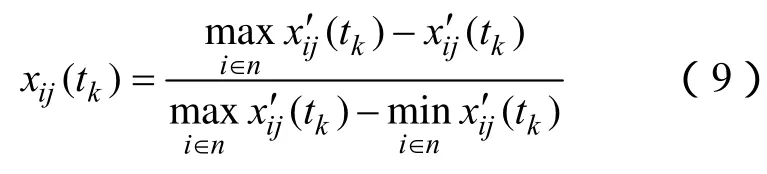
不同量纲的指标经过标准化处理后转化为无量纲的标准化指标，xij(tk)∈[0,1]，消除了量纲的影响。

3.2 方案不同时段的静态评估模型

在得到各方案标准化后的指标值组成的时序立体数据表｛xij(tk)｝后，通过线性加权模型对待评估方案si在tk时段所有指标集结得到该时段的评价值yi(tk)，集结模型为

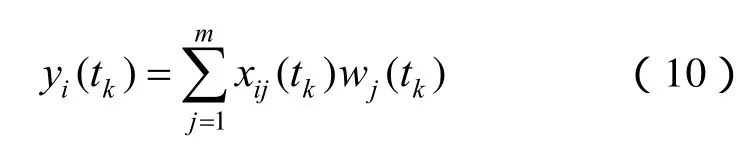
式中，wj(tk)为第tk时段指标j的综合权重。

3.3 指标综合权重的计算

本文采用组合赋权法计算指标的综合权重，以专家赋权法确定不同时段指标的主观权重，拉开档次法计算指标的客观权重[19]，两者相结合得到指标综合权重。

以专家赋权法确定不同时段各指标的主观权重时，由于事实的不确定性和模糊性及专家知识结构和专业的差别等因素的影响，采用模糊语言权重更适合，模糊数则为刻画语言模糊程度提供了有效工具，引入三角模糊数表示模糊权重，能够有效地将模糊权重转化为确定数值，模糊权重与相应三角模糊数如表2所示。

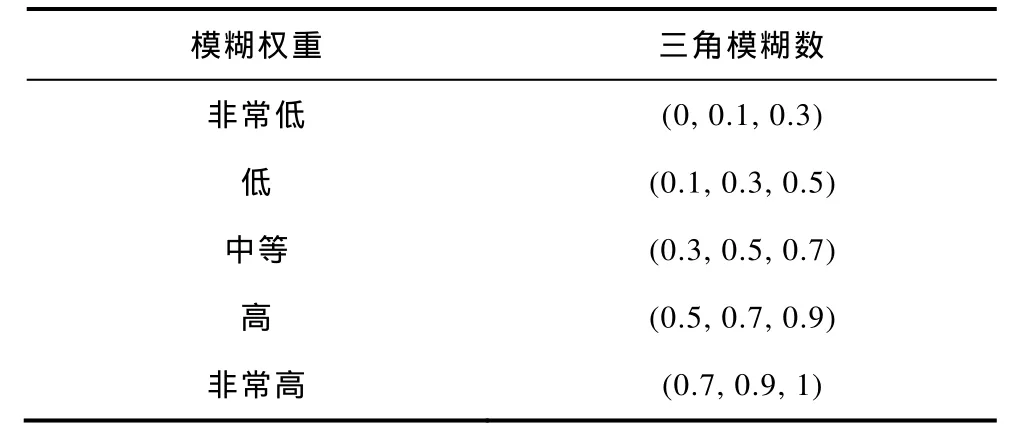
表2 模糊权重与相应三角模糊数Tab.2 Fuzzy weight and the corresponding triangular fuzzy numbers

设有L(L≥ 1)位专家对不同时段的指标进行赋权决策，第g位专家给出的tk时段第j个指标的模糊权重为，则综合各专家决策信息的模糊权重为

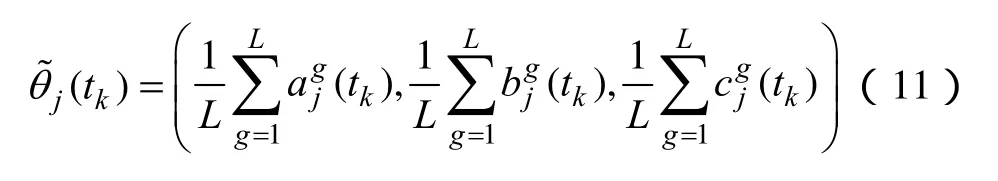
将指标的模糊权重明晰化处理，转化公式为

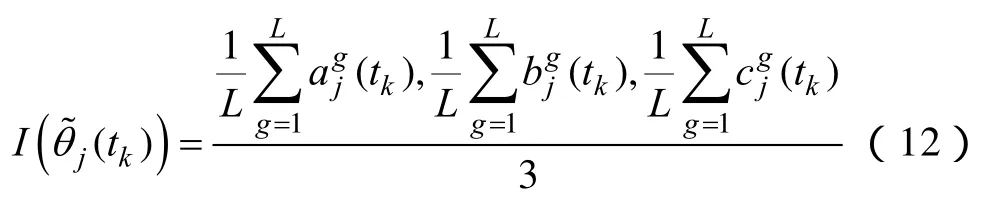
则tk时段指标j归一化后的主观权重为

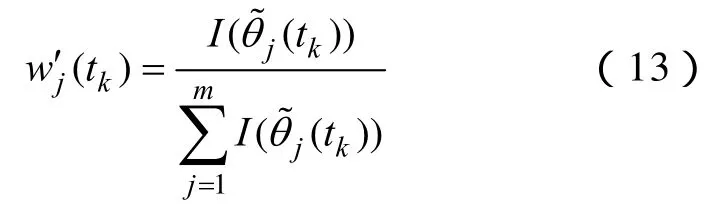
由式（11）～式（13）即可求出tk时段包含所有指标的主观权重向量W'(tk)。

各指标的客观权重采用尽可能体现出方案间差异的拉开档次法确定，对于tk时段，由各待评估方案在此阶段的所有指标组成的矩阵为，即时序立体数据表｛xij(tk)｝在tk时段的取值，设，求取Htk的最大特征值λmax()及相对应的特征向量，归一化后的特征向量即为tk时段指标的客观权重向量则tk时段指标j的综合权重wj(tk)可由主观权重和客观权重得到，即

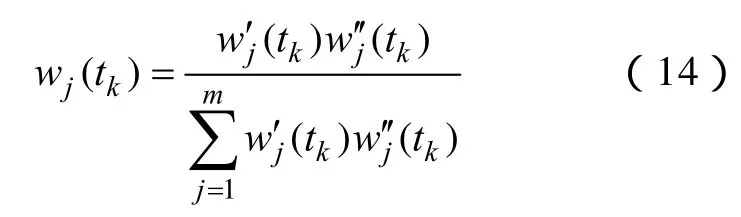
4 方案动态综合评估

方案动态评估结果是黑启动阶段和后续恢复阶段评价值的综合体现，在求得方案si在黑启动阶段和后续恢复阶段各自静态评价值的基础上，通过对两个时段评价值在时间维上再次集结得到所有时段的动态综合评价值，本文引入时序加权平均（Time Ordered Weighted Averaging Operator，TOWA）算子和时序几何平均（Time Ordered Weighted Geometric Averaging Operator，TOWGA）算子组成的混合算子模型进行集结。

4.1 TOWA-TOWGA动态综合评估模型

时序加权平均（TOWA）算子和时序几何平均（TOWGA）算子是诱导有序信息集结算子簇中用于时序信息集结的算子，以下是两种算子的定义[19]。

定义1 令T=｛1,2,…,t｝ ，称为由二维数组构成的TOWA对，ui为时间诱导分量，ai为数据分量，时序加权平均(TOWA)算子定义为

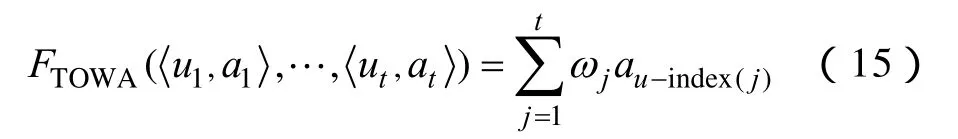
式中，ω=(ω1,ω2,…,ωt)T是与FTOWA相关的加权向量，ωj∈［0,1］，是按ui时间先后排列的第j个TOWA对数据分量，称FTOWA是t维TOWA算子。

定义2 令T=｛1,2,…,t｝ ，称为由二维数组构成的TOWGA对，ui为时间诱导分量，ai为数据分量，时序几何平均(TOWGA)算子定义为

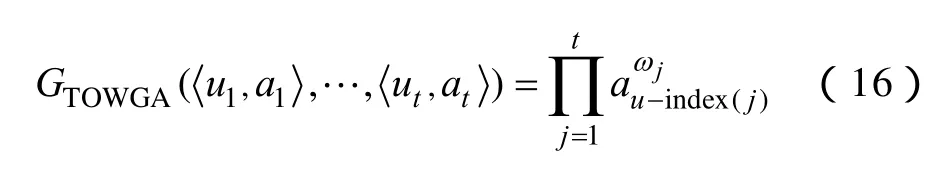
式中，ω=(ω1,ω2,…,ωt)T是与GTOWGA相关的加权向量，ωj∈［0,1］ ，是按ui时间先后排列的第j个TOWGA对数据分量，则称GTOWGA是t维TOWGA算子。

由式（15）和式（16）可知两种算子的实质是将时间诱导分量ui按时间顺序排序后所对应的数据分量进行加权集结，但在数据集结过程中侧重点不同，TOWA算子对时序数据线性加权，是“和性”的，突出了较大评价值的作用，TOWGA算子采用乘法合成法对时序数据集结，是“积性”的，突出了不同时段评价值的均衡性，因此，将两种算子组合使用，能够兼顾两种算子的特点，结果将更为合理[20]。

在由方案si黑启动阶段评价值和后续恢复阶段评价值分别构成的算子对及不同时段权重wtk的基础上，对两个时段评价值再次集结时，本文采用以下由TOWA算子和TOWGA算子组成的混合算子模型进行集结，即

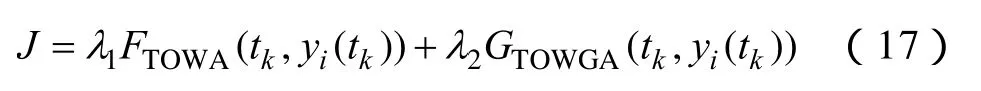
式中，λ1、λ2为比例因子，λ1≥0，λ2≥0，且λ1+λ2=1，分别表示TOWA算子和TOWGA算子在混合模型中所占的比重。

4.2 不同时段时间权重的确定

在以 TOWA-TOWGA混合算子模型对方案si黑启动阶段和后续恢复阶段两个时段的评价值再次集结时，时间权重wtk的确定极为关键，直接关系到综合评价结果的合理性。本文以非线性熵值规划法[19]求解各时段的时间权重，在求解权重前先给出时间度λ和权重向量熵I的定义。

定义3 由各时段时间权重wtk和总时段数K，时间权重向量熵I定义为

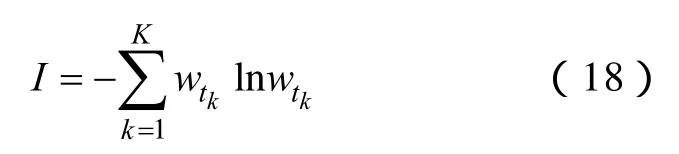
定义4 时间度λ定义为

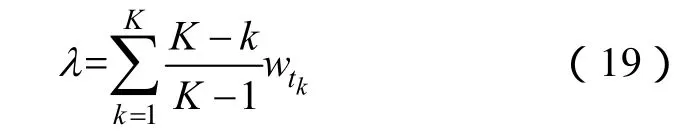
时间权重向量熵I反映了集结过程中时间权重包含信息的程度。时间度λ体现了集结过程中决策者对不同时段的重视程度。λ∈［ 0,1］，λ取值越接近0，表明越注重后续恢复阶段评价值；取值越接近1，则越重视黑启动阶段评价值，λ取值标度见表3。

表3 时间度标度取值Tab.3 The value of time degree

非线性熵值规划法求解各时段的时间权重wtk的准则是在事先确定时间度λ的前提下，即在体现决策者时序决策偏好下，尽可能地挖掘待评估方案的信息和时序上的差异信息来寻求最优的时间权向量，使主观决策信息与客观评价数据得到有效的融合，权重更为准确，可用如下的优化模型表示

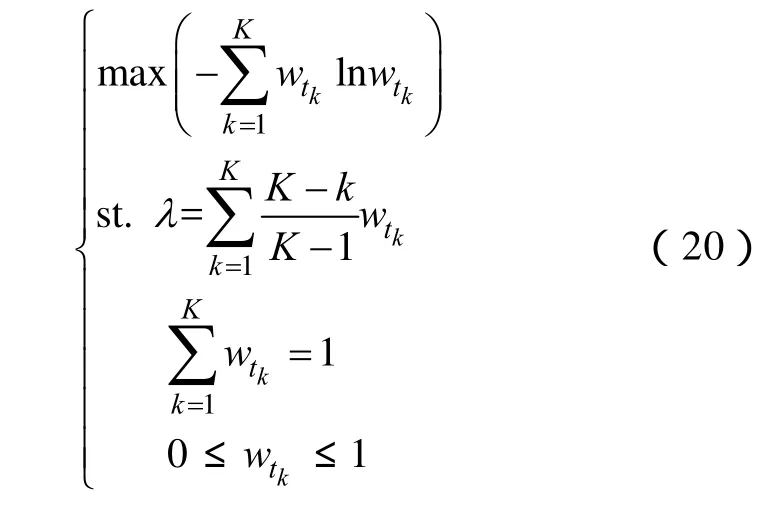
通过求解此非线性规划模型即可得到黑启动阶段和后续恢复阶段的最优时间权重wt1和wt2。

4.3 动态综合评估流程

综上所述，扩展黑启动方案动态综合评估的具体步骤如下：

（1）分别建立黑启动阶段和后续恢复阶段的评估指标，构建评估指标体系，确定待评估方案集S。

（2）对S中每一方案si，在黑启动阶段恢复形成的小系统基础上完成后续恢复，计算各方案不同时段的指标值，组成时序立体数据表，并标准化处理。

（4）由线性加权模型对方案si不同时段分别实施静态评估，得到黑启动阶段评价值yi(t1)和后续恢复阶段评价值yi(t2)。

（5）在给定时间度λ值的前提下，由非线性熵值规划法求解得到黑启动阶段和后续恢复阶段的各自时间权重wt1和wt2。

（6）由不同时段时间权重和TOWA-TOWGA混合算子模型对方案si两个时段的评价值再次集结，得到最终的动态综合评价结果。

5 算例分析

5.1 算例描述

采用本文提出的动态评估方法对图2所示的新英格兰10机39节点系统中扩展黑启动方案实施评估，技术校验合格的 3个扩展黑启动方案见表 4，各台被启动机组参数见表5，PG为机组额定功率；Pcr为机组启动功率；Kp为机组升负荷率；Tk为机组启动时间；根据相加的两项的相对重要性，转换系数σ取0.5，μ取1。黑启动阶段采取零起升压方式对恢复路径充电，设充电时间为0.25h。

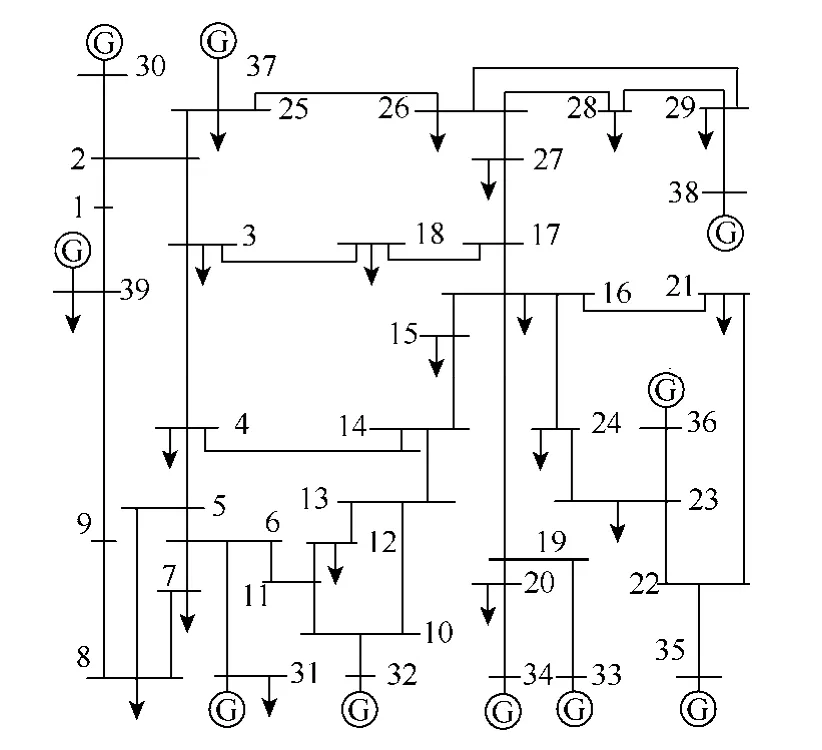
图2 新英格兰10机39节点系统Fig.2 New England 10-unit 39-bus power system

表4 技术可行的扩展黑启动方案Tab.4 Technically feasible extended black-start schemes

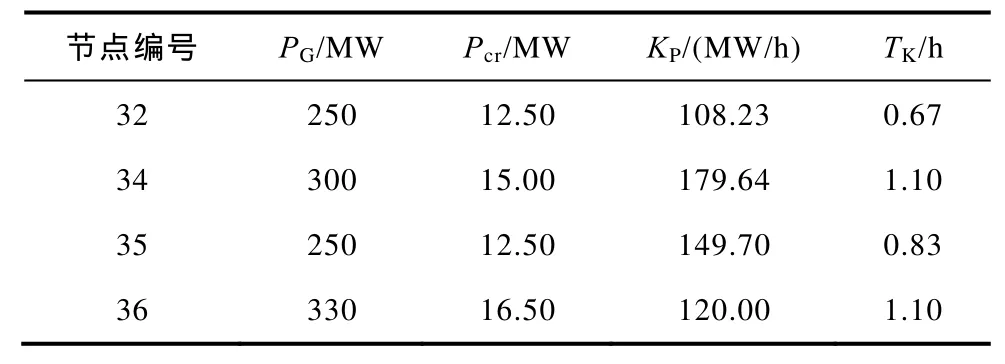
表5 被起动机组的参数Tab.5 Parameters of the units to be restored

5.2 计算结果

利用文献[22]提出的“分时步、整体寻优”重构策略在上述不同扩展黑启动方案形成的局部网络基础上完成后续恢复，方案1和方案2一个时步完成后续恢复，方案3两个时步完成后续恢复。由于后续恢复前期时步的启动功率、恢复的机组、负荷相对后期时步更重要，权重系数wcr.n、wG.n和wL.n第一时步取1，第二时步取0.6。由机组及系统参数通过 BPA等仿真程序计算得到各待评估方案不同时段的指标值，组成的时序立体数据见表6。

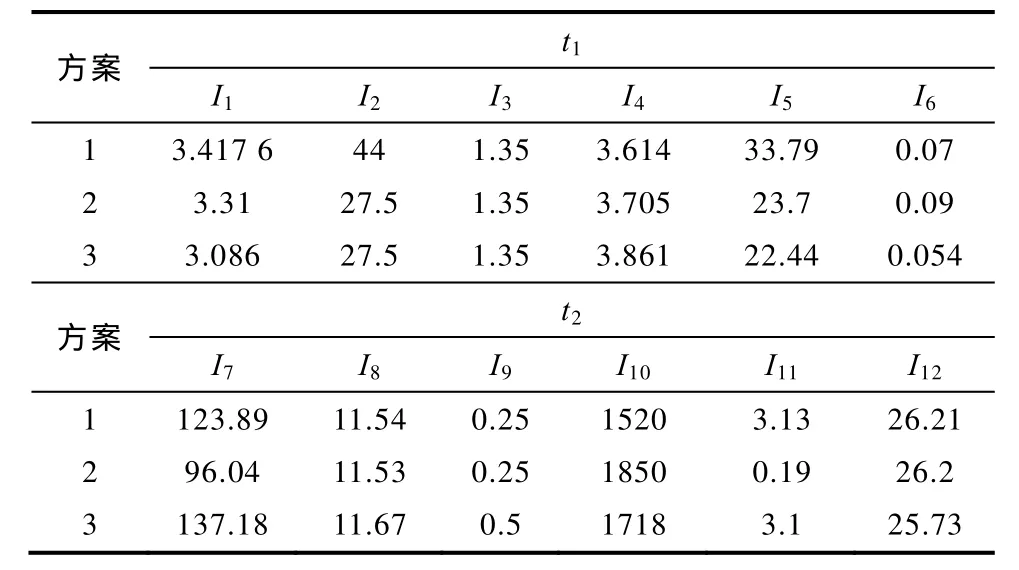
表6 评估方案时序立体数据表Tab.6 Timing order cubic data table of plans

通过3位专家对黑启动阶段和后续恢复阶段指标赋权决策，由式（11）～式（13）得到两个时段的主观权重向量分别为

对时序立体数据表6中各指标值经过式（8）和式（9）标准化处理后，由拉开档次法可得到两个时段指标的客观权重向量为

主客观权重由式（14）相结合得到各时段指标综合权重向量为

以线性加权模型（见式（10））对各方案不同时段分别进行静态评估，得到各时段的评价值，见表7。

表7 各方案不同时段评价值Tab.7 Assessment value of different period for plans

在时间度λ取0.5，即同样重视黑启动阶段和后续恢复阶段，两个时段的评价值同等重要，比例因子λ1、λ2均取0.5，表示两种算子在混合算子模型中比重均衡。求解非线性规划模型（见式（20））得到相应的时间权重向量为=(0.5,0.5)。

最后对待评估方案在黑启动阶段和后续恢复阶段的评价值由式（17）再次集结，得到各方案的动态综合评估结果，见表 8。以文献[17]中采用的主成分分析法计算得到各方案的评估结果也列于表8中。

表8 各方案评价值Tab.8 Assessment value of plans

将传统的逼近理想解法 TOPSIS应用于各方案不同时段的评估，由层次分析法得到的两个时段的权重为

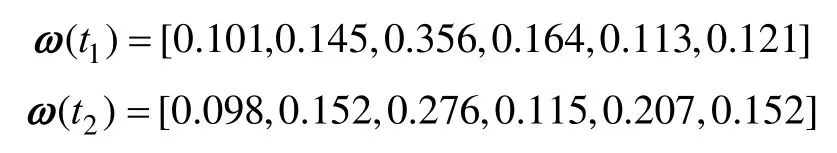
各待评估方案在两个不同时段的评估结果见表9。

表9 各方案不同时段评估结果Tab.9 Assessment results of different period for plans

5.3 结果分析

由于各方案恢复的机组及形成的局部小网络不同，由表6可知各方案在黑启动阶段的指标值不完全相同，因此在表7中各方案黑启动阶段的评价值不同，在黑启动阶段方案3评价值最大；由表6可知以不同方案形成的局部网络为基础的后续恢复过程也存在差异，方案1后续恢复评价值最大。由表7可知，黑启动阶段恢复效果好的方案在其后续恢复效果未必好。若仅以黑启动阶段的评价值作为优选方案的依据，则方案3为最优，但其后续恢复的效果不够理想，在考虑对后续恢复影响的动态综合评估中，方案2为整体上最优的方案，因此将方案对后续恢复的影响纳入到方案动态综合评估中是必要的。

由表8和表9可知，本文方法对各方案两个时段的评估结果与传统 TOPSIS法结果一致，动态综合评估结果与文献[17]主成分分析法评价结果一致，但 TOPSIS法得到的是各方案不同时段的评估结果，而主成分分析法的计算结果只能反映方案的整体评价结果，无法反映方案在黑启动阶段的恢复效果和对后续恢复的影响，也忽略了决策者的决策偏好。动态综合评估既能从整体上对方案进行评估，又体现了方案不同阶段的动态恢复水平，融入决策者的决策信息后，评价结果更全面。

6 结论

本文提出了一种基于时序动态理论的扩展黑启动方案动态综合评估方法。构建了反映黑启动阶段和后续恢复阶段恢复特征的指标体系，主客观相结合的组合赋权法使指标权重更加合理，采用线性加权模型对各时段内指标集结得到不同时段的评价值。非线性熵值规划法能够有效根据决策者的时序偏好求取各时段的最优时间权重，以时序加权平均算子和时序几何平均算子组成的混合算子模型对两个时段的评价值再次集结，克服了目前黑启动方案评估中未考虑对后续恢复影响的不足。算例分析验证了所提出方法的有效性，可为扩展黑启动方案的决策提供科学依据，对大停电后的快速恢复起到重要作用。

[1] 张东霞,姚良忠,马文媛. 中外智能电网发展战略[J]. 中国电机工程学报,2013,33(31): 1-14.

Zhang Dongxia,Yao Liangzhong,Ma Wenyuan.Development strategies of smart grid in China and abroad[J]. Proceedings of the CSEE,2013,33(31):1-14.

[2] 汤涌,卜广全,易俊. 印度“7. 30”、“7. 31”大停电事故分析及启示[J]. 中国电机工程学报,2012,32(25): 167-174.

Tang Yong,Bu Guangquan,Yi Jun. Analysis and lessons of the blackout in Indian power grid on July 30 and 31,2012[J]. Proceedings of the CSEE,2012,32(25): 167-174.

[3] 顾雪平,钟慧荣,贾京华,等. 电力系统扩展黑启动方案的研究[J]. 中国电机工程学报,2011,31(28):25-32.

Gu Xueping,Zhong Huirong,Jia Jinghua,et al.Extended black-start schemes of power systems[J].Proceedings of the CSEE,2011,31(28): 25-32.

[4] 刘艳,顾雪平,张丹. 基于数据包络分析模型的电力系统黑启动方案相对有效性评估[J]. 中国电机工程学报,2006,26(5): 32-37.

Liu Yan,Gu Xueping,Zhang Dan. Data envelopment analysis based relative effectiveness assessment of power system black-start plans[J]. Proceedings of the CSEE,2006,26(5): 32-37.

[5] 林济铿,蒋越梅,岳顺民,等. 基于DEA/AHP模型的电力系统黑启动有效方案评估[J]. 电力系统自动化,2007,31(15): 65-70.

Lin Jikeng,Jiang Yuemei,Yue Shunmin,et al.Assessment of effective schemes for power system blackstart based on DEA/AHP[J]. Automation of Electric Power Systems,2007,31(15): 65-70.

[6] 吴烨,房鑫炎,张焰,等. 电网黑启动的广义模式评估算法[J]. 电工技术学报,2011,26(3): 155-161.

Wu Ye,Fang Xinyan,Zhang Yan,et al. Generalized assessment algorithm for power grid black-start modes[J]. Transactions of China Electrotechnical Society,2011,26(3): 155-161.

[7] 钟慧荣,顾雪平. 基于模糊层次分析法的黑启动方案评估及灵敏度分析[J]. 电力系统自动化,2010,34(16): 34-37.

Zhong Huirong,Gu Xueping. Assessment of power system black-start schemes based on fuzzy analytic hierarchy process and its sensitivity analysis[J]. Automation of Electric Power Systems,2010,34(16): 34-37.

[8] 林济铿,李童飞,赵子明,等. 基于熵权模糊综合评价模型的电力系统黑启动方案评估[J]. 电网技术,2012,36(2): 115-120.

Lin Jikeng,Li Tongfei,Zhao Ziming,et al. Assessment on power system black-start schemes based on entropy weighted fuzzy comprehensive evaluation model[J].Power System Technology,2012,36(2): 115-120.

[9] 吴烨,房鑫炎. 基于模糊 DEA 模型的电网黑启动方案评估优化算法[J]. 电工技术学报,2008,23(8):101-106.

Wu Ye,Fang Xinyan. Data envelopment analysis based optimal fuzzy algorithm for assessing power grid black-start plans[J]. Transactions of China Electrotechnical Society,2008,23(8): 101-106.

[10] 张志毅,陈允平. 基于模糊多属性决策的黑启动方案优选[J]. 高电压技术,2007,33(3): 42-45.

Zhang Zhiyi,Chen Yunping. Optimization of power system black-start schemes based on the fuzzy multiple attribute decision-making method[J]. High Voltage Engineering,2007,33(3): 42-45.

[11] 王宏,林振智,文福拴,等. 基于区间数的黑启动决策方法[J]. 电力系统自动化,2013,37(11): 26-31.

Wang Hong,Lin Zhenzhi,Wen Fushuan,et al. A black-start decision-making method based on interval values[J]. Automation of Electric Power Systems,2013,37(11): 26-31.

[12] 林振智,文福拴,薛禹胜,等. 基于多属性群决策特征根法的智能电网黑启动决策[J]. 电力系统自动化,2010,34(5): 18-23.

Lin Zhenzhi,Wen Fushuan,Xue Yusheng,et al.Black-start decision-making in smart grids using mutiattribute group eigenvalue method[J]. Automation of Electric Power Systems,2010,34(5): 18-23.

[13] 林振智,文福拴,薛禹胜,等. 智能电网黑启动群体决策的可靠性分析[J]. 电力系统自动化,2010,34(9): 17-22.

Lin Zhenzhi,Wen Fushuan,Xue Yusheng,et al.Reliability analysis on the group decision-making results of black-start strategies in smart grids[J].Automation of Electric Power Systems,2010,34(9):17-22.

[14] Liu Weijia,Lin Zhenzhi,Wen Fushuan,et al. Analysis and optimization of the preferences of decision makers in black-start group decision makering[J]. IET Generation,Transmission & Distribution,2013,7(1): 14-23.

[15] 林振智,文福拴,周浩. 熵权决策理论及其在黑启动决策中的应用[J]. 电力系统及其自动化学报,2009,21(6): 26-33.

Lin Zhenzhi,Wen Fushuan,Zhou Hao. Entroy weight based decision-making theory and its application to black-start decision-making[J]. Transaction of Power Systemand Automation,2009,21(6): 26-33.

[16] 曾顺奇,林振智,文福拴,等. 基于 Vague集理论的黑启动决策模型与方法[J]. 电力系统自动化,2011,35(2): 18-22.

Zeng Shunqi,Lin Zhenzhi,Wen Fushuan,et al. A vague theory based model and approach for blackstart decision-making[J]. Automation of Electric Power Systems,2011,35(2): 18-22.

[17] 赵达维,刘天琪,李兴源,等. 电网黑启动方案评价指标体系及应用[J]. 电力系统自动化,2012,36(10): 7-12.

Zhao Dawei,Liu Tianqi,Li Xingyuan,et al. Blackstart scheme evalution indicator system and its application[J]. Automation of Electric Power Systems,2012,36(10): 7-12.

[18] 郭亚军. 一种新的动态综合评价方法 J]. 管理科学学报,2002,5(2): 49-54.

Guo Yajun. New theory and method of dynamic comprehensive evaluation[J]. Journal of Management Science in China,2002,5(2): 49-54.

[19] 郭亚军,姚远,易平涛. 一种动态综合评价方法及应用[J]. 系统工程理论与实践,2007,27(10): 154-158.

Guo Yajun,Yao Yuan,Yi Pingtao. A method and application of dynamic comprehensive evaluation[J].Systems Engineering Theory & Practice,2007,27(10):154-158.

[20] 郭亚军,钟田丽. 兼顾“功能性”与“均衡性”的综合评价方法及应用[J]. 中国软科学,2001(6):104-106.

Guo Yajun,Zhong Tianli. Multiple attribute evaluation method taking account of functionality and proportionality and its application[J]. China Soft Science,2001(6): 104-106.

[21] 欧阳森,石怡理,刘洋. 基于纵横向拉开档次法的电能质量动态评估[J]. 华南理工大学学报(自然科学版),2013,41(4): 27-32.

Ou Yangsen,Shi Yili,Liu Yang. Dynamic evaluation of power quality based on vertical and horizontal scatter degree method[J]. Journal of South China University of Technology(Natural Science Edition),2013,41(4): 27-32.

[22] X Gu,H Zhong. Optimization of network reconfiguretion based on a two-layer unit-restarting framework for power system restoration[J]. IET Generation,Transmission & Distribution,2011,6(7): 693-700.

[23] 王亮,刘艳,顾雪平,等. 综合考虑节点重要度和线路介数的络重构[J]. 电力系统自动化,2010,34(12): 29-33.

Wang Liang,Liu Yan,Gu Xueping,et al. Skeleton network reconfiguration based on node importance and line betweenness[J]. Automation of Electric Power Systems,2010,34(12): 29-33.