基于继电保护与改进算法的储能电站选址定容

杨 炼 范春菊 邰能灵 黄文焘

（上海交通大学电子信息与电气工程学院 上海 200240）

1 引言

近年来储能电站已成为配电网调峰填谷、提高系统稳定性及实现需求侧管理的一种有效手段。但伴随着储能技术的飞速发展，越来越多的问题暴露出来，如储能电站不同接入点及接入容量对配电网原有继电保护的影响，对调峰填谷、系统稳定性等的效果等，这些都值得电力系统工作人员重视与研究[1]。

当不同容量的储能电站接入配电网络不同的节点时，原来简单的单电源辐射网络变为了复杂的多电源网络，可能会导致原有保护出现灵敏度降低、拒动及误动等问题，由此给配电网的运行和控制带来多方面的影响。储能电站与一般的分布式电源不同，其有三种运行状态：放电、充电和备用状态，因此配电网的继电保护不能简单地将修改保护定值作为应对储能电站接入的方法，而应根据保护的特性进行优化协调，在储能电站选址定容时进行适当的规划，以减小对配电网原有保护的影响，使原有保护不至失效[2-6]。

随着计算机技术和现代智能优化技术的发展，配电网中分布式电源规划从最初的人工筛选方式发展为通过计算机计算自动生成站址的方式，其优化方法也由传统的数学优化方法上升到现代的智能优化算法，但目前所采用的很多智能方法均有其不足之处。混沌优化方法具有易跳出局部极小点、搜索速度快和全局渐近收敛等一系列优点，但当搜索空间大的时候其效果并不显著。免疫算法因其具有较好的种群多样性、记忆性及稳定性而被广泛应用，它能迅速将问题的解限制在一个较小区间内，但在小区间内搜索到满意解的效率还不能令人满意。禁忌搜索具有较强的爬山能力，搜索过程中可以跳出局部最优解，具有避免早熟的能力，但禁忌搜索是串行的，搜索效率低，并且禁忌搜索对初始解具有较强的依赖性[7-9]。

本文根据各种智能算法的特点，针对配电网的特点，设计了一种将混沌免疫禁忌混合使用的改进算法，同时考虑配电网继电保护动作特性不变的约束条件，对储能电站的选址定容进行了优化，使储能电站接入后可以稳定系统电压，减小网损，并且保护可以正确动作，以提高系统运行的可靠性。

2 储能电站与继电保护特性

2.1 储能电站工作特性

在储能电站种类中，电池储能是现在研究的热门方向之一[10-13]。电池作为储能模块，直流电能经由 PWM控制的逆变器逆变为交流后接入电网。在其进行充电储能时，储能电站的工作特性相当于一个负载，额定工作电流即最大充电电流NI''。在正常放电运行时，储能电站额定电流与额定容量成正比。即

由于逆变器器件的特性限制，储能电站的最大输出电流一般为其额定输出电流的2倍。当配电网发生短路时，在储能电站输出电流I未达到2倍额定电流时，储能电站根据其控制策略的要求，输出功率或电压维持不变，输出电流增大；当故障输出电流增大到 2IN时，受逆变器器件限制，储能电站输出电流将维持在2IN不变。

2.2 配电网的保护特性

传统配电网的特点是呈放射形结构并由单电源供电，配电网的继电保护是以此为基础设计的。当储能电站等分布式电源接入配电网后，配电网的结构将发生改变。当配电网发生故障时，除了系统向故障点提供故障电流外，分布式电源也将对故障点提供故障电流，改变继电保护的保护范围和灵敏度，给各线路保护的上、下级配合带来问题。分布式电源安装位置和容量等因素都将对配电网的继电保护造成影响。

图1所示为典型配电网结构。图中，Z1～Z5为相应线路的阻抗，S1～S5为相应的断路器，E为系统电源，ZS为系统阻抗，DG为储能电站，ZG为储能电站内阻。

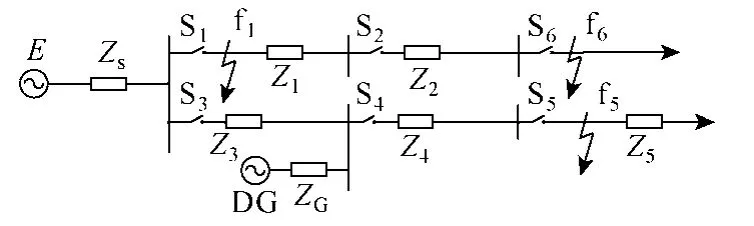
图1 含储能电站的配电网结构图Fig.1 Structure diagram of the distribution network with an energy storage station

配电网馈线保护一般配置为三段式电流保护和反时限过电流保护。当储能电站接入配电网时，接入点上、下游及相邻线路若发生故障，储能电站输出电流将会使得接入点到故障点线路中的短路电流增大，超过电流保护的整定值而造成误动作。如图1中下游f5点发生相间故障时，若储能电站容量较大，产生的助增电流将使得S4处的电流保护误动；若上游f1处发生相间故障时，S3处的电流保护可能会误动；若相邻线路上f6处发生相间故障时，S1、S2处的电流Ⅰ段保护和过电流保护可能会误动，S1处的电流Ⅱ段保护可能会误动。

反时限过电流保护的动作特性方程为

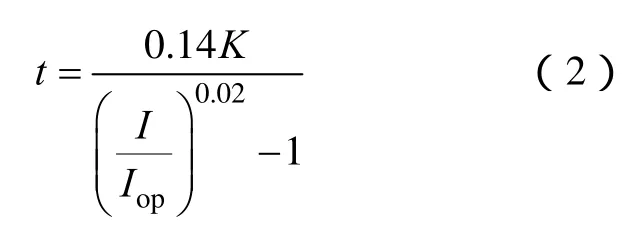
由于反时限过电流继电器的动作时间特性为对数特性，当短路电流变大、动作时间变短时，相邻保护间的动作时间间隔也将变短。当相邻保护的动作时间间隔小于保护装置的固有动作时间时，将出现保护的误动作[14]。

3 储能电站选址定容的数学建模

3.1 配电网节点编码

配电网的节点进行建模编码时，传统建模方法是对节点进行一维编码，即从1～n依次编码。储能电站接入配电网后，需要分析接入点上、下游及相邻馈线的保护受到的影响，传统一维编码无法解决各节点间的联系问题，即无法按照某一规律来确定上下游及相邻馈线的关系。本文根据文献[15]所述二维编码，提出多维编码方法以解决计算机算法中计算继电保护的问题。

如图2所示配电网，节点的编码为3维4位。在第一级节点处，从上至下只有1个节点，则第一位编码为1，其余位为0，即1000；在第二节点处，从上到下有15个节点，则第二位和第三位依次编码为01～15（如果第二级节点数目较少，只有9个，则只占一位，编码为0～9），即1010～1150；在第三节点处，对于从上一级中同一节点引出的第三级节点，编码第四位从1～n进行编码。即多维编码规律为：①每一级节点占用一维；②每一维的节点根据是否从上一级同一节点引出而决定是否从1开始编码；③在对m维进行编码时，m维后面的维均编为0。

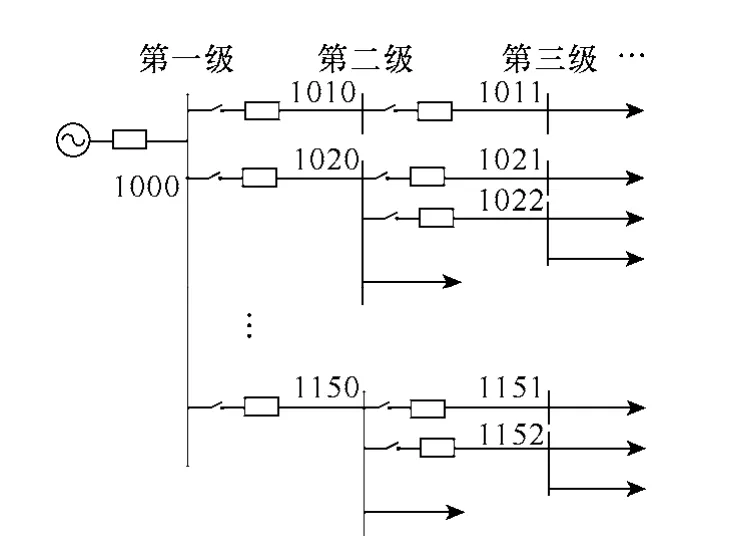
图2 配电网多维编码图Fig.2 Multidimensional code of the distribution network

采用多维编码后，在程序运算时，只需对节点相应维进行判断与加减，即可计算出上、下游及相邻馈线的电气量。

3.2 优化目标与约束条件

储能电站除了电池外，还要建立相应的监控、变流等系统，故而总体造价比较昂贵，但对于一定容量的储能电站，增加或减小一部分容量所对应的投资花费较小。因此，根据负荷特性、政策等确定了采用储能电站后，在进行选址定容时不必再考虑储能电站的经济性。储能电站选址定容问题可描述为：在规划目标负荷分布已知的情况下，为了满足一定的负荷需求，以最小运行费用等作为目标函数，以节点电压等作为约束条件，确定储能电站的位置、容量。

3.2.1选址定容优化目标

储能电站的选址定容优化目标函数一般包括技术目标和经济目标。经济目标主要包括系统的有功网损最小，技术目标则包括系统各负荷节点的电压水平最好（关系到电能质量问题），一般采用下式所示单目标优化模型[16-19]

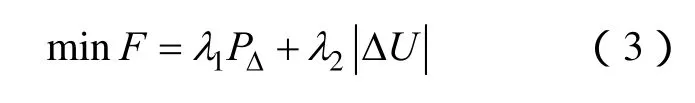
式中，PΔ为配电网络有功损耗的无量纲值；ΔU为平均电压偏移的无量纲值；λ1、λ2为反映对电网运行经济性和电压稳定性偏好的权重，且λ1+λ2=1。

3.2.2选址定容约束条件

（1）节点有功功率、无功功率约束以及节点电压安全约束

无论储能电站处于何种工作状态，网络要满足潮流方程的约束，且节点电压均要求维持在允许范围内。

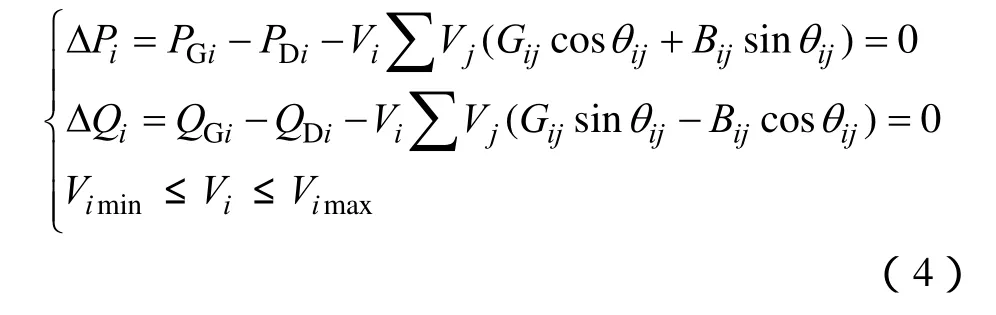
式中，PGi、QGi分别为节点i上发电机的有功和无功出力；PDi、QDi分别节点i上负荷的有功和无功功率；Gij、Bij和θij分别为节点i、j之间的电导、电纳和电压相角差。

（2）继电保护约束

由于逆变器输出电流受到限制，不会过大，因此配电网发生短路等故障时，储能电站对短路电流的影响较小，因此以储能电站接入后不使原有保护失效为约束条件。

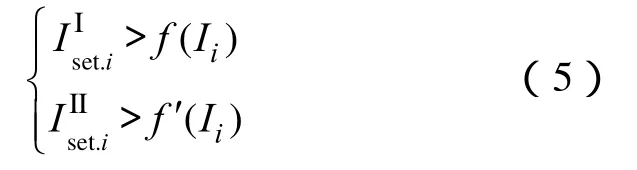
其中，对于下游保护

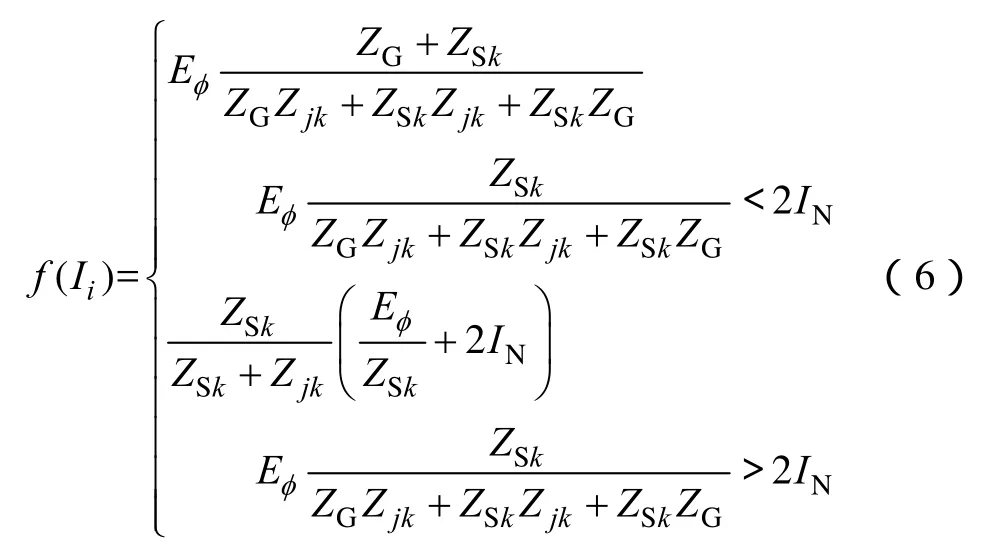
式中，j点为馈线上i节点下游的节点；k点为储能电站接入的节点；ZG为储能电站阻抗；ZSk为系统电源到节点k的阻抗；Zjk为节点j到节点k的阻抗；Eφ为系统等效电源相电动势。将式中Zjk换成Zkm，即可得f'(Ii)，m为节点j的下一级节点。

对于上游保护

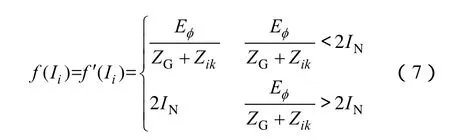
对于相邻馈线保护

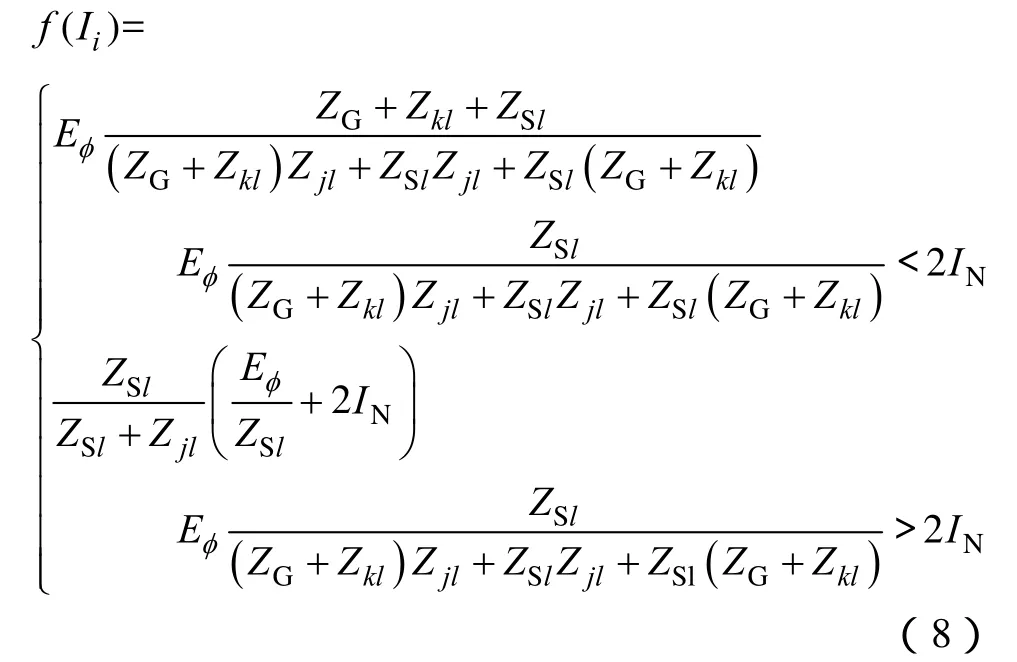
式中，l点为储能电站所在馈线与相邻馈线的共同流出节点。将式中Zkl换成Zkm，即可得f'(Ii)。

过电流保护按照最大负荷电流来整定，在相关支路中，储能电站接入点下游支路出口处负荷电流增加最大，控制此处最大负荷电流在允许范围内，即可确保配电网各处过电流保护均不会误动。

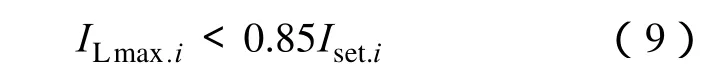
相邻反时限过电流保护的动作时间间隔应不小于时间差ε，储能电站接入点下游相邻两处保护的动作时间问题比其他地方严重，因此确保这两处保护的动作时间间隔满足要求，即可保证其他保护的时间间隔也满足要求。即储能电站接入点下一级节点出口处发生短路时，要求

式中，q为馈线上储能电站接入点的下一级节点。

4 改进的混沌免疫混合算法

混沌优化算法是把待求问题的变量从解空间变换到混沌空间，然后利用混沌变量具有随机性、规律性和遍历性的特点进行搜索求解的一种算法；免疫算法是基于生物免疫系统理论，在进化算法理论框架基础上引入免疫算子而形成的一种优化算法；禁忌搜索是一种亚启发式随机搜索算法，它从一个初始可行解出发，选择一系列的特定搜索方向作为试探，选择实现让特定的目标函数值变化最多的移动，并建立禁忌表以避免陷入局部最优解。本文结合这三种智能算法的特点，针对配电网的特性，设计了一种适用于配电网选址定容的改进混沌免疫混合算法。

4.1 算法原理概述

由于配电网为辐射结构，进行储能电站的选址时，在迭代初期将出现大量亲和度相近的抗体；储能电站的容量受电池组数量控制，可连续变化，但其在配电网的接入点一般按支路节点改变，因此选址定容问题中既包含连续变量，又包含离散的节点变量。由于混沌优化适合在连续变量区间内实行遍历寻找最优解，因此适合求解连续变量优化解；而免疫禁忌混合算法可更方便地处理离散变量。因此在储能电站的选址定容过程中，首先用免疫禁忌混合算法对接入节点进行离散变量的优化求解：先利用免疫算法进行全局搜索，使抗体群中的个体比较稳定地分布在解空间的大部分区域，迭代一定次数后，采用免疫禁忌混合算法，把禁忌搜索算法引入到免疫算法的变异操作中，继续进行迭代求解。每次迭代中求出接入点可行解后，再使用混沌算法对当前接入点进行储能电站容量的寻优，将综合结果与终止条件比较，若不满足则进行下一轮迭代交替求解。通过这样的混沌优化与免疫禁忌优化的交替求解可使两者的优化结果互为基础、相互利用，在迭代初期提高了搜索的效率及准确度，迭代后期有效搜索到最优解附近的解空间，避免陷入局部最优，保证了混沌免疫混合策略的整体寻优效率。

4.2 算法中的关键技术点

4.2.1混沌映射和混沌扰动方式的确定

目前混沌优化算法常用的是LogiStic方法，该方法产生的混沌变量迭代方法方便，计算量小[7]。该方法产生混沌序列的迭代公式为

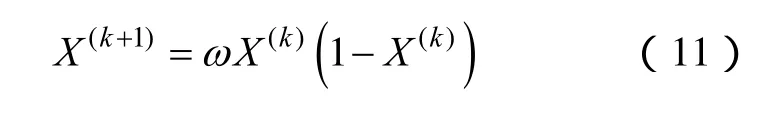
式中，X为混沌变量，0≤X≤1；k是混沌迭代次数，k=1,2,…；ω是控制参数，ω=4时系统完全处于混沌状态，其混沌空间为（0,1），不动点为0.25、0.5和0.75。对于随机扰动的确定 参照文献[20]的改进方法，令

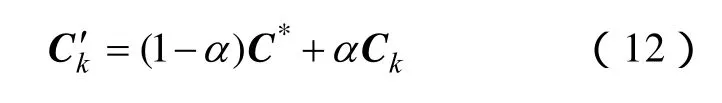
式中，C*为当前最优值映射到[0,1]后形成的向量，称为最优混沌向量；Ck为迭代k次后的混沌向量，C'k为施加随机扰动后的混沌向量；0＜α＜1，搜索初期希望变量变动较大，这需要较大的α；随着搜索进程的深入，变量逐渐接近最优点，故需要设计较小的α，以便在小范围内搜索，因此本文算法中α按下式确定。

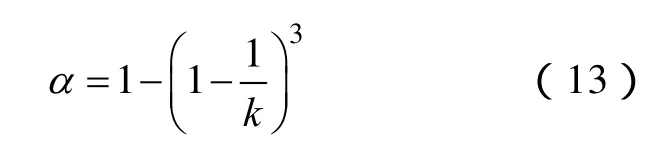
4.2.2变异算子的选择

（1）标准变异算子。变异在遗传算法中，个体染色体的个别基因座上的基因值发生变化，它是遗传算法过程中产生新个体的辅助手段，决定了遗传算法的局部搜索能力。

免疫算法的亲和力aff为

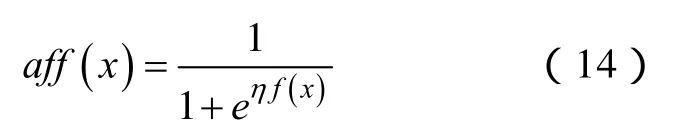
式中，f(x)为抗体x对应的可行解的目标函数值；0＜η＜1。则标准变异选择为

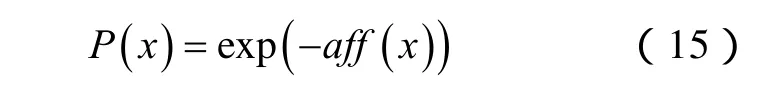
（2）加入禁忌搜索的改进变异算子。免疫禁忌混合搜索算法中，采用禁忌搜索算法作为变异算子，把一个要变异的抗体作为禁忌搜索的输入，把禁忌搜索得到的解作为变异的新个体。已被考虑过的解组成禁忌表T，在建立邻域候选解V集时可从中移除在禁忌表中的解。每个中间解xi+1都通过求解如下最优化问题来得到

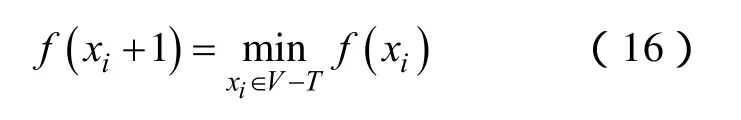
式中，邻域V取决于当前解为xi。当数目kmax次重复迭代后没有改进或所有的邻域候选解被禁忌，V-T=0时，算法将停止。

任一抗体z，其邻域可构造为

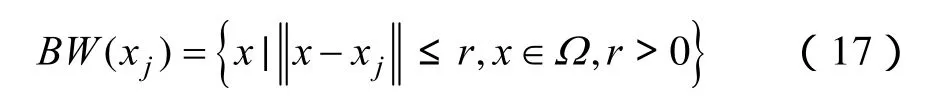
4.3 基于改进算法的选址定容求解步骤

4.3.1算法流程图

本文针对含储能电站的配电网所设计的改进混沌免疫混合算法的运算流程如图3所示。

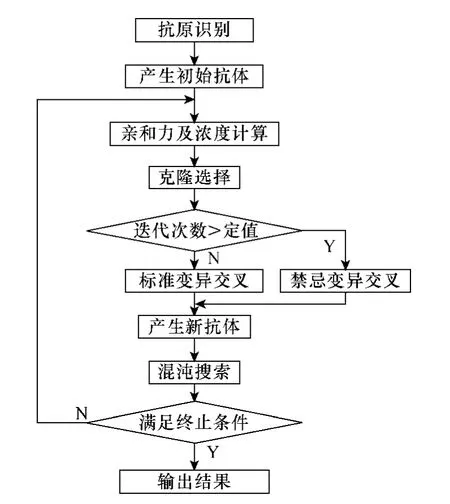
图3 改进混合算法的流程图Fig.3 Flow chart of improved hybrid algorithm

4.3.2求解步骤

（1）输入原始的数据及所需参数。输入该问题所有相关的电气数据，并设置该优化算法的运行参数。

（2）确定编码方式及产生初始抗体群。本文对离散的接入节点变量采用 2.1.1节所述的多维编码法，对连续的容量控制变量采用十进制整数编码，能较好地满足寻优的要求。储能电站接入节点组成N个随机的初始单一抗体，从第二次迭代开始，将混沌搜索得到的最优容量与接入节点组成复合抗体。

（3）选择操作及参数调节。采用连续潮流法来计算抗体群中每个复合抗体的评价值，即抗体与抗原的亲和力，按照升序进行排列，组成抗体群A1。

（4）从抗体群A1中选择前η%个复合抗体，将容量从中剥离，对单一抗体进行克隆操作，产生的克隆数与亲和力的大小成正比例关系，组成抗体群A2，根据迭代次数是否超过设定值来决定采用标准变异或禁忌变异在抗体群A2进行变异、交叉操作，产生抗体群A3。

（5）从A1中淘汰亲和度低的抗体后形成抗体群A4。模拟了免疫响应中约有ρ%抗体的自然消亡及部分亲和力小的抗体自然消亡。

（6）对抗体群中的抗体进行亲和力计算，并且按照亲和力的大小进行免疫选择，同时考虑免疫选择后的抗体和A4抗体之间的相似度（消除相似度高的抗体），选出整体亲和力大的抗体组成A5，将A5加入到A4中组成新一代的抗体群A6，即记忆抗体群。

（7）随机产生新的抗体群A7，并同时考虑抗体群A7与A6抗体之间的相似度，相似度高的抗体淘汰掉，重新产生抗体，补充到A7中，将A7加入到A6中，组成新一代抗体群A8。

（8）针对抗体群A8中的单一抗体，调用混沌算法搜索最优容量值，组成复合抗体群A9。

（9）检查优化免疫算法迭代结束条件，如果达到，则进行下一步，否则跳到步骤（3）。

（10）输出优化结果，结束。

5 算例分析

为了验证本文所提算法的可行性，选择福建湄洲岛 10kV配电网的实例进行计算与分析，如图 4所示。本文用 Matlab 2010编制了混沌免疫混合算法程序，在程序中相关数值的选取分别为N=10，η%=40%，ω=4，λ1=0.3，λ2=0.7，最大迭代次数为100。在该配电网中，除平衡节点以外，电源节点都作为PV节点处理，其他节点都属于PQ节点，PQ节点的电压允许变化范围为0.95～1.05（pu），储能电站规划接入容量范围为5～10MV·A。

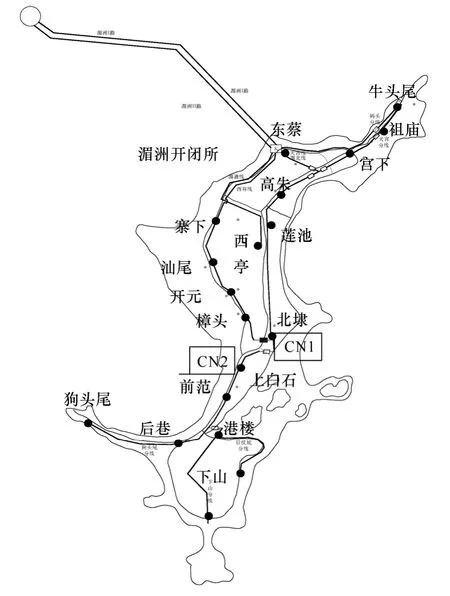
图4 湄洲岛配电网结构图Fig.4 Structure diagram of the distribution network in Meizhou island

分别采用免疫算法与改进混沌免疫混合算法对该配电网进行储能电站的选址定容，其中系统网损以 100MW 为基准值。考虑到上述各算法均受各种随机因素的影响，故对每种算法各运行 30次取平均值进行对比。

图4中CN1（北埭）为传统免疫算法的选址结果，CN2（上白石）为改进混沌免疫混合算法的选址结果。两种算法得出的结果均未使配电网原有保护失效。采用两种算法求解时其他参数见表 1；采用改进算法时，在各节点接入储能电站后使得原有保护不失效的最大准入容量见表 2。为验证改进算法优化结果的准确性，表3列举了在若干节点分别接入不同容量时的潮流计算分析结果。

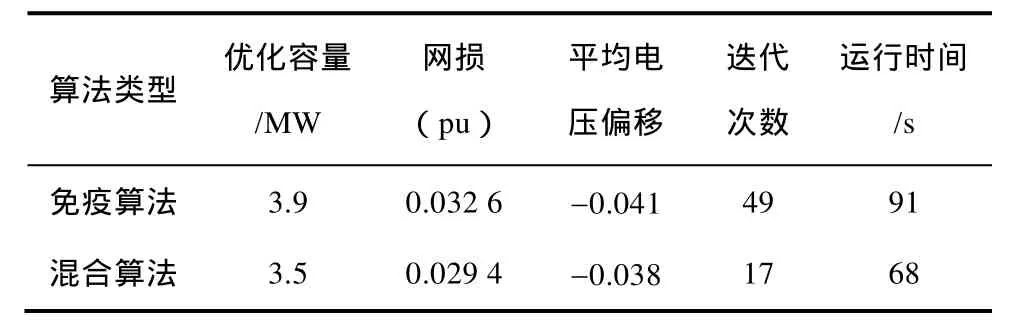
表1 两种算法运算结果对比Tab.1 Comparing results of the two algorithms

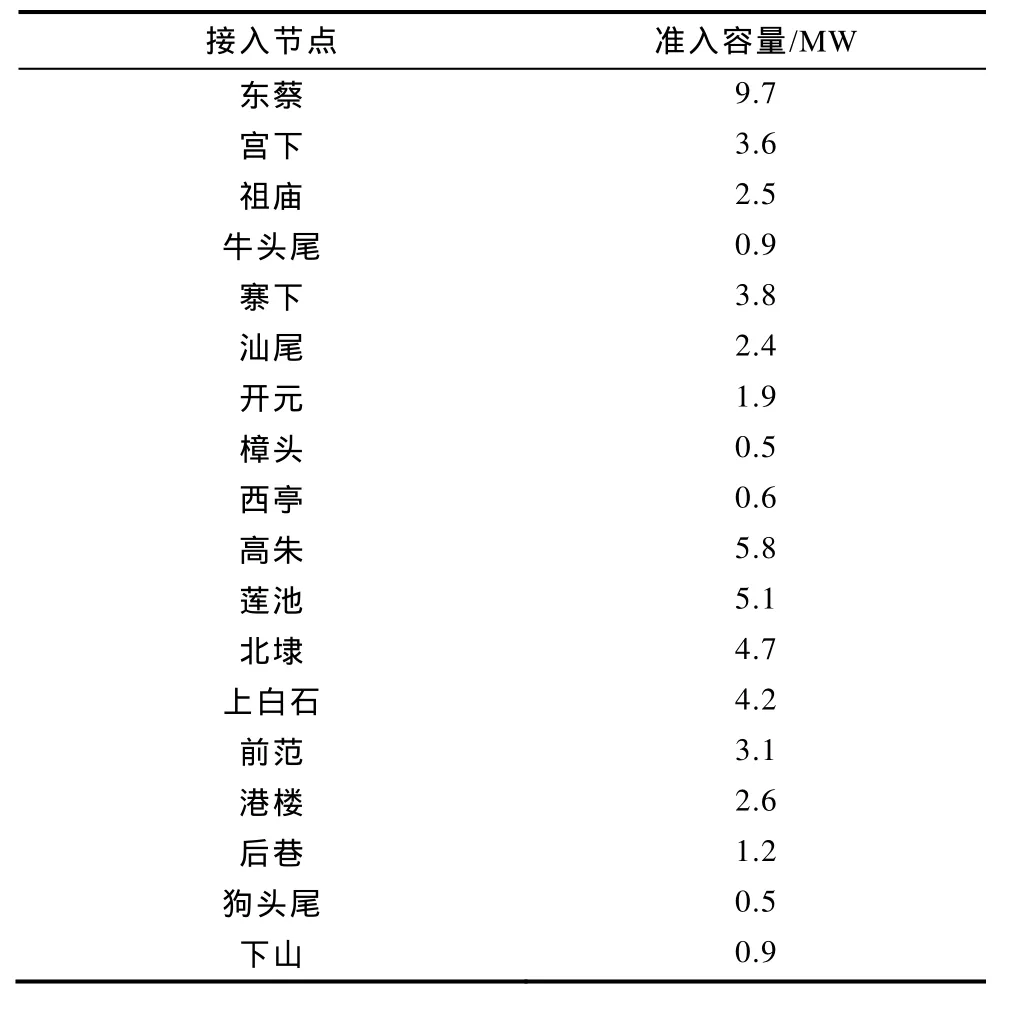
表2 改进算法下各节点最大准入容量Tab.2 Maximum access capacity of each node under improved algorithm

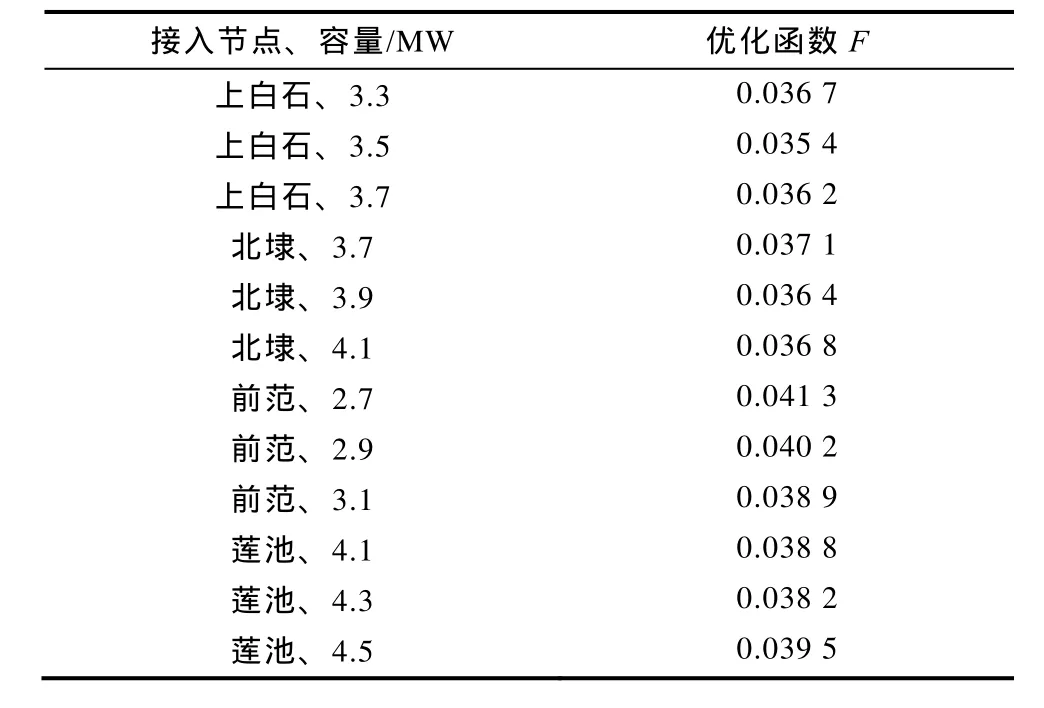
表3 改进算法下若干节点及容量运算结果Tab.3 Calculation results of some nodes and capacities under improved algorithm

由表1可知，采用改进混沌免疫混合算法求取的网损与节点平均电压偏移均低于采用免疫算法求取的值，由于混合算法加入禁忌搜索作为变异算子，每次迭代时要调用混沌算法搜索最优容量值，因此单次搜索用时比免疫算法长，但在迭代次数上混合算法减少了，所以总的计算耗时比免疫算法短。由此可知本文设计的混合算法能更快、更精确地寻优，更适合配电网络的储能电站的选址定容。

6 结论

本文对储能电站特性及其对配电网继电保护的影响进行了分析，并针对配电网特点提出了一种将混沌免疫禁忌混合算法用于选址定容的新方法。以网络有功损耗与平均电压偏移作为优化目标，将储能电站输出电流及继电保护动作特性加入到约束条件中，将禁忌搜索作为免疫算法设定迭代次数后的变异算子，采用混沌搜索对容量进行最优化，通过交叉搜索，可有效地搜索到储能电站选址定容的全局最优解。最后将该方法用于福建某岛屿配电网络的选址定容实例中，经多次优化计算，将其计算结果与单纯的免疫算法进行对比分析，从而验证了该方法的合理性和实用性，为配电网络中储能电站的选址定容提供了新的途径和方法。

[1] 丁明,徐宁舟,毕锐. 用于平抑可再生能源功率波动的储能电站建模及评价[J]. 电力系统自动化,2011,35(2): 66-72.

Ding Ming,Xu Ningzhou,Bi Rui. Modeling of BESS for smoothing renewable energy output fluctuations[J]. Automation of Electric Power Systems,2011,35(2): 66-72.

[2] Teng J,Luan S,Lee D,et al. Optimal charging/discharging scheduling of battery storage systems for distribution systems interconnected with sizeable PV generation systems[J]. IEEE Transactions on Power Systems,2012: 1-9.

[3] Habeebullah Sait H,Arul Daniel S. New control paradigm for integration of photovoltaic energy sources with utility network[J]. International Journal of Electrical Power & Energy Systems,2011,33(1): 86-93.

[4] 王江海,邰能灵,宋凯,等. 考虑继电保护动作的分布式电源在配电网中的准入容量研究[J]. 中国电机工程学报,2010,30(22): 37-43.

Wang Jianghai,Tai Nengling,Song Kai,et al.Penetration level permission of for DG in distributed network considering relay protection[J]. Proceedings of the CSEE,2010,30(22): 37-43.

[5] 张艳霞,代凤仙. 含分布式电源配电网的馈线保护新方案[J]. 电力系统自动化,2009,33(12): 71-74.

Zhang Yanxia,Dai Fengxian. New schemes of feeder protection for distribution networks including distributed generation[J]. Automation of Electric Power Systems,2009,33(12): 71-74.

[6] 冯希科,邰能灵,宋凯,等. DG容量对配电网电流保护的影响及对策研究[J]. 电力系统保护与控制,2010,38(22): 156-165.

Feng Xike,Tai Nengling,Song Kai,et al. Research on the impact of DG capacity on the distribution network current protection and counter measure[J].Power System Protection and Control,2010,38(22):156-165.

[7] 刘惠姣. 基于混合智能算法的配电网无功优化的研究[D]. 保定: 华北电力大学,2009.

[8] 熊虎岗,程浩忠,胡泽春,等. 基于混沌免疫混合算法的多目标无功优化[J]. 电网技术,2007,31(11):33-37.

Xiong Hugang,Cheng Haozhong,Hu Zechun,et al. A hybrid algorithm based on chaos optimization algorithm and immune algorithm for multi-objective optimal reactive power flow[J]. Power System Technology,2007,31(11): 33-37.

[9] 曾令全,罗富宝,丁金嫚. 禁忌搜索–粒子群算法在无功优化中的应用[J]. 电网技术,2011,35(7):129-133.

Zeng Lingquan,Luo Fubao,Ding Jinman. Application of particle swarm optimization algorithm integrated with tabu search in reactive power optimization[J].Power System Technology,2011,35(7): 129-133.

[10] Gupta A,Saini R P,Sharma M P. Hybrid energy system sizing incorporating battery storage: an analysis via simulation calculation[C]. Third International Conference on Power Systems,India,2009: 1-6.

[11] Yahyaie F,Soong T. Optimal operation strategy and sizing of battery energy storage systems[C]. 25th IEEE Conference on Electrical and Computer Engineering,Canadian,2012: 1-4.

[12] 王贵斌,赵俊华,文福拴,等. 配电系统中电动汽车与可再生能源的随机协同调度[J]. 电力系统自动化,2012,36(19): 22-29.

Wang Guibin,Zhao Junhua,Wen Fushuan,et al.Stochastic optimization dispatching of plug-in hybrid electric vehicles in coordination with renewable generation in distribution systems[J]. Automation of Electric Power Systems,2012,36(19): 22-29.

[13] 丁明,徐宁舟,毕锐. 负荷侧新型电池储能电站动态功能的研究[J]. 电力自动化设备,2011,31(5): 1-7.

Ding Ming,Xu Ningzhou,Bi Rui. Dynamic model of new-type battery energy storage system at demand side[J]. Automation of Electric Power Systems,2011,31(5): 1-7.

[14] 花丽丹,陆于平,吴罡,等. DG容量在分布式发电中对数字保护影响的研究[J]. 中国电力,2008,41(3): 12-16.

Hua Lidan,Lu Yuping,Wu Gang,et al. Study on the effect of distributed generation size on digital protective device in distribution system[J]. Electric Power,2008,41(3): 12-16.

[15] 杨晓强,谭耀东,朱宁洪,等. NoC节点编码及路由算法的研究[J]. 计算机科学,2009,36(3): 86-89.

Yang Xiaoqiang,Tan Yaodong,Zhu Ninghong,et al.Node encoding and routing algorithm for network on chip[J]. Computer Science,2009,36(3): 86-89.

[16] 高付良,张鹏,赛雪,等. 考虑负荷不确定性的变电站选址定容[J]. 电力系统保护与控制,2010,38(15): 75-80.

Gao Fu1iang,Zhang Peng,Sai Xue,et al. Substations locating and sizing in uncertainty load environment[J].Power System Protection and Control,2010,38(15):75-80.

[17] 胡国强,贺仁睦. 梯级水电站多目标模糊化调度模型及其求解方法[J]. 电工技术学报,2007,22(1):154-158.

Hu Guoqiang,He Renmu. Model and algorithm of multi-objective fuzzy optimal scheduling for cascaded hydroelectric power plant[J]. Transactions of China Electrotechnical Society,2007,22(1): 154-158.

[18] 陈道君,龚庆武,张茂林,等. 考虑能源环境效益的含风电场多目标优化调度[J]. 中国电机工程学报,2011,31(13): 10-17.

Chen Daojun,Gong Qingwu,Zhang Maolin,et al. Multiobjective optimal dispatch in wind power integrated system incorporating energy-environmental efficiency[J]. Proceedings of the CSEE,2011,31(13): 10-17.

[19] 夏澍,周明,李庚银. 分布式电源选址定容的多目标优化算法[J]. 电网技术,2011,35(9): 115-121.

Xia Shu,Zhou Ming,Li Gengyin. Multi-objective optimization algorithm for distributed generation locating and sizing[J]. Power System Technology,2011,35(9): 115-121.

[20] 王子才,张彤,王宏伟. 基于混沌变量的模拟退火优化方法[J]. 控制与决策,1999,14(4): 381-384.

Wang Zicai,Zhang Tong,Wang Hongwei. Simulated annealing algorithm based on chaotic variable[J].Control and Design,1999,14(4): 381-384.