基于高漏抗式消弧线圈的配电网单相接地故障状态辨识

刘味果 赵 邈 毛柳明 周恒逸

（国网湖南省电力公司电力科学研究院 长沙 410007）

1 引言

谐振接地方式是指电网中性点通过消弧线圈与大地相连的方式，由德国人W. Peterson在1916年最早提出来，经过多年的发展，谐振接地方式在世界许多国家的中压配电系统中得到广泛的应用[1-5]。相对其他配电网中性点接地方式而言，采用谐振接地方式的配电网的有两大特点:其一，当系统单相弧光接地故障发生时，可以利用消弧线圈产生的感性电流对电容电流进行补偿，减小残流，实现快速熄弧；另外，在接地电弧熄灭后，降低了故障相电压的恢复速度，能够有效抑制电弧的重燃。在中国，随着谐振接地技术的不断发展，许多中压变电站都采用了谐振接地方式，同时也出现了多种不同类型的自动跟踪补偿消弧线圈[6,7]。如早期的调匝式消弧线圈，由有载开关改变电感线圈的抽头档位来实行电感值的调节，另外由广东电力科学研究院发明的高漏抗式消弧线圈，通过改变可控硅的触发延迟角度来改变电感值[8,9]。

在采用谐振接地的配电网中，当接地故障消失后，消弧线圈不能准确判别单相接地消失，没有及时退出补偿状态或者投入防止串联谐振设施，消弧线圈与系统对地电容发生串联谐振，产生“虚幻接地”现象。“虚幻接地”现象严重危害了系统的正常运行，目前最通常采用的措施是增大消弧线圈的脱谐度。然而脱谐度增加牺牲了补偿精度，必然会在系统单相接地时使接地点故障点残流增大，同时也使得接地电弧熄灭后故障相电压的恢复速度加快，无法最大限度发挥谐振接地技术特点，从而影响到灭弧效果。如何在实现对电容电流准确补偿的同时避免发生串联谐振，其关键在于消弧线圈装置能够准确辨识配电网单相接地故障状态，在接地消失后能够自动改变补偿装置。

随着谐振接地技术的发展，各国专家学者对消弧线圈的特性进行了大量研究[10-12]，但对如何准确识别系统的接地状态目前尚没有文献记载，缺乏完善的处理办法。本文在高漏抗式消弧线圈的基础上，充分利用其动态调节、快速响应的特点，通过监测接地消失时系统中性点电压暂态变化过程，提出以跟踪电压频率的变化来判别系统接地状态的方法，采用该算法提高了消弧线圈补偿效果，也解决了消弧线圈产生串联谐振问题，计算机仿真结果和试验室试验证实了所提判别方法的可行性。

2 谐振接地系统接地故障消失时的暂态过程[13]

谐振接地系统发生单相接地故障时，零序回路可以用图1所示的电路等效。图中，Ua为故障相电源电压；U0为系统零序电压（即消弧线圈的端电压）；Rd为故障点接地电阻；L为消弧线圈的电感值；C0为系统三相对地分布电容等效电容值；R0为消弧线圈的损耗以及线路对地泄漏和电晕等损耗值。

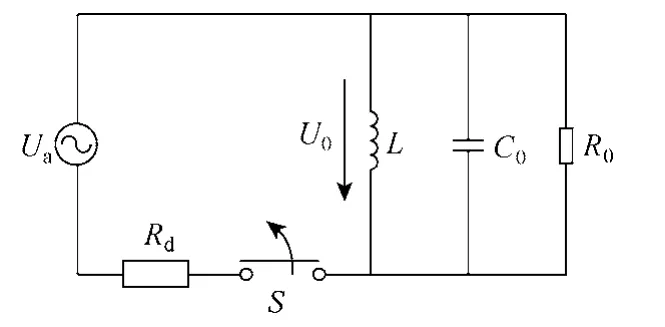
图1 接地故障时谐振接地系统的零序回路等效电路Fig.1 The equivalent circuit for the earth-fault in the resonance network before the extinguishing of the arc

当接地故障点电流过零电弧熄灭时，相当于图1中开关S断开，此时系统的零序回路等效电路可以由图2来表示，图中，Uk为系统的三相不平衡电压（由于Uk相对于Ua而言完全可以忽略，因此在图1没有考虑Uk的影响）。

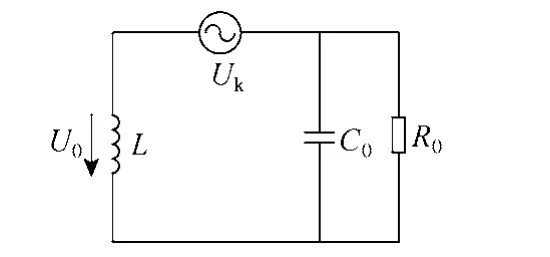
图2 接地故障消失时零序回路等效电路Fig.2 The equivalent circuit for the earth-fault in the resonance network after the extinguishing of the arc

接地消失时，系统零序电压可以表示为暂态和稳态两部分，稳态部分可以表示为

考虑等值损耗R0值较小，脱谐度v为

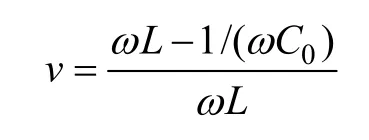
式（1）可以表示为

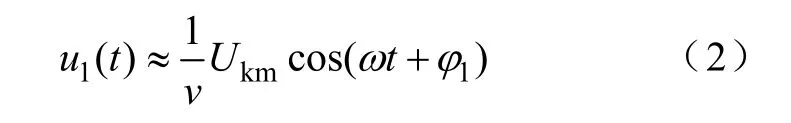
系统零序电压暂态部分可以表示为

最后，由式（2）和式（3）得到了当配电网单相接地故障消失时，系统零序电压的表达式为

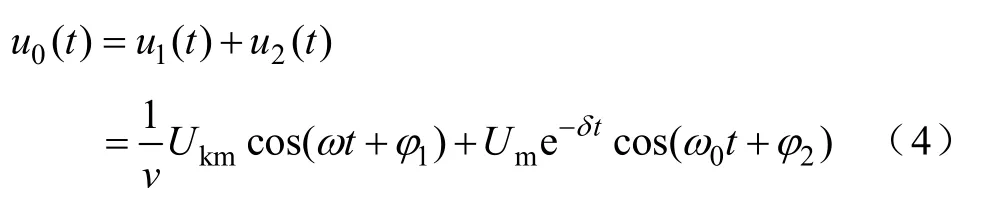
在配电网单相接地故障消失前，系统零序电压U0的幅值决定于图1中所示零序回路的各参数，但此时U0角频率等于配电网电源角频率ω。当接地电弧熄灭，故障消失时，如图2所示，消弧线圈电感与系统对地电容形成一个LC串联谐振回路。式（4）表明接地消失时，系统零序电压存在一个角频率为ω0且逐渐衰减的暂态变化量。为了减小单相接地时接地点残流，消弧线圈的电抗越接近于系统对地电容容抗补偿效果越好，即

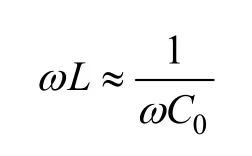
因此，接地消失时图 2中的电路自振频率ω0约等于系统电源频率ω，即脱谐度v→0。当v→0，由于等值损耗R0的存在不可能出现u1(t)的幅值趋于∞，但系统中性点仍会产生很高的谐振电压，这就是谐振接地系统中出现的“虚幻接地”现象。而且ω0≈ω，u2(t)以系统电源的角频率衰减，简单的波形频率分析仅仅根据零序电压幅值很难辨识出系统的状态。

为了使单相接地故障后电弧能快速熄灭，要求残流越小越好，即v越小越利于电弧熄灭，但v越小使得接地消失时，由于串联谐振造成系统零序电压过高，同时也不利于消弧线圈退出补偿状态的判断，可能会产生“虚幻接地”。因此，灭弧和消弧线圈退出的不同要求使得对脱谐度v的要求是相互矛盾的。传统消弧线圈为了保证不对系统产生负面影响，一般将脱谐度设定在5%～20%之间，即牺牲了部分消弧线圈的补偿性能来避免接地消失时发生串联谐振。

3 高漏抗式消弧线圈在接地消失时的暂态分析

高漏抗式消弧线圈在零序电压一个周波内，晶闸管相对于电压波形正反向对称导通，导通时消弧线圈电流是对一次电压的积分；而晶闸管关断时，则消弧线圈输出电流受滤波阻抗影响。在配电系统发生接地故障时，晶闸管导通角度的变化只是影响了消弧线圈电流的大小。但在接地消失时，由第二章的讨论可知，此时消弧线圈与配电网对地电容形成自由振荡回路，因而零序电压存在一个角频率为回路自振频率的暂态分量。由于高漏抗式消弧线圈与其他类型的消弧线圈在基本原理结构上有区别，使得其在接地消失时暂态零序电压的变化有所不同，以下分析讨论了晶闸管不导通和导通两种情况下暂态零序电压的变化。

3.1 晶闸管不导通时零序电压变化

如果接地消失时消弧线圈晶闸管始终处于截止状态，根据第2节谐振接地系统的暂态分析以及高漏抗式消弧线圈的原理，可以得到接地消失时系统的等效电路如图 3所示。图中，uk为系统的三相不平衡电压；C0为系统三相对地电容；L0为消弧线圈的励磁阻抗与母线 PT零序阻抗并联的等效电感；L1＋L2为高漏抗式消弧线圈的短路阻抗的电感值；u0为系统零序电压。

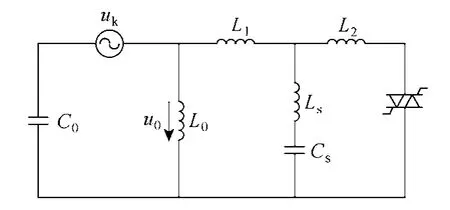
图3 接地消失时系统的等效电路Fig.3 The equivalent circuit when thyristors are turned off

为简单起见，滤波回路只考虑三次滤波器件Ls、Cs，另外电路中不考虑消弧线圈和系统的损耗。令

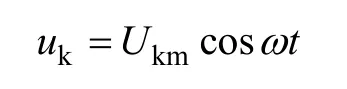
其拉普拉斯变换为

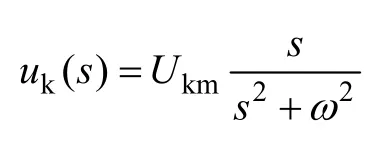
由于晶闸管处于截止状态，流过L2的电流为零，则有

其中令

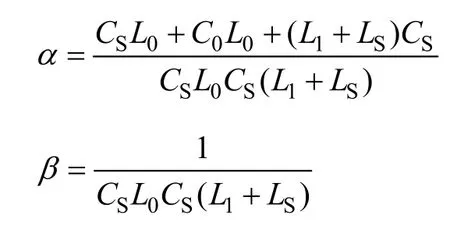
则有

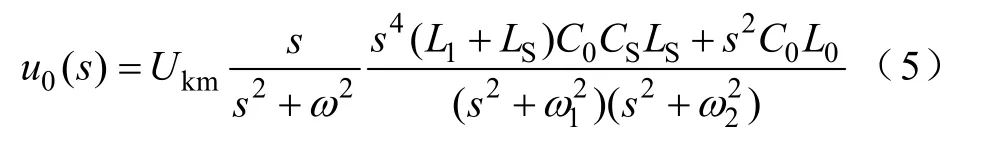
式中

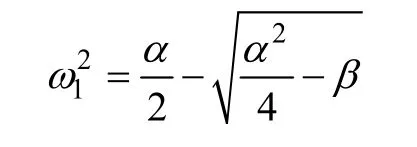
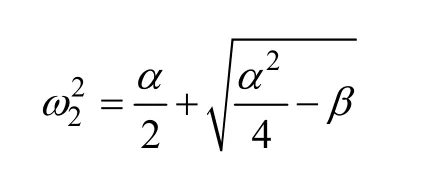
由零序电压u0的拉氏变换表达式（5）可以得到，在系统单相接地故障消失时，零序电压的暂态过程存在多个频率分量，分别为ω、ω1和ω2。取实例进行计算，10kV/500kV·A的消弧线圈的各参数为 :L0=26.42H，Ls=0.287H，Cs=3.92μF，L1+L2=0.224H，系统三相对地电容为C0=28μF，对应系统电容电流为 53.2A，计算结果为f1=5.5Hz，f2=136.9Hz。零序暂态电压的f1频率分量主要取决于系统对地电容与消弧线圈励磁阻抗的参数，而高频f2暂态分量，则取决于滤波回路和系统对地电容的参数。

依据上述参数选择合适的电容器组在试验室进行模拟试验，试验过程中晶闸管一直处于截止状态，图4表示接地故障消失时零序电压、电流的暂态波形。从图4a中可以看到零序电压呈低频振荡衰减，并迭加了幅值较小的高频振荡，如频谱图4b所示，试验结果与理论计算是基本一致的。从图 4a中可以看到，零序电压在振荡衰减过程中随着电压幅值降低，频率也随之减小，与计算中频率为恒定值有所不同，这是由于变压器的励磁电抗非线性造成的。

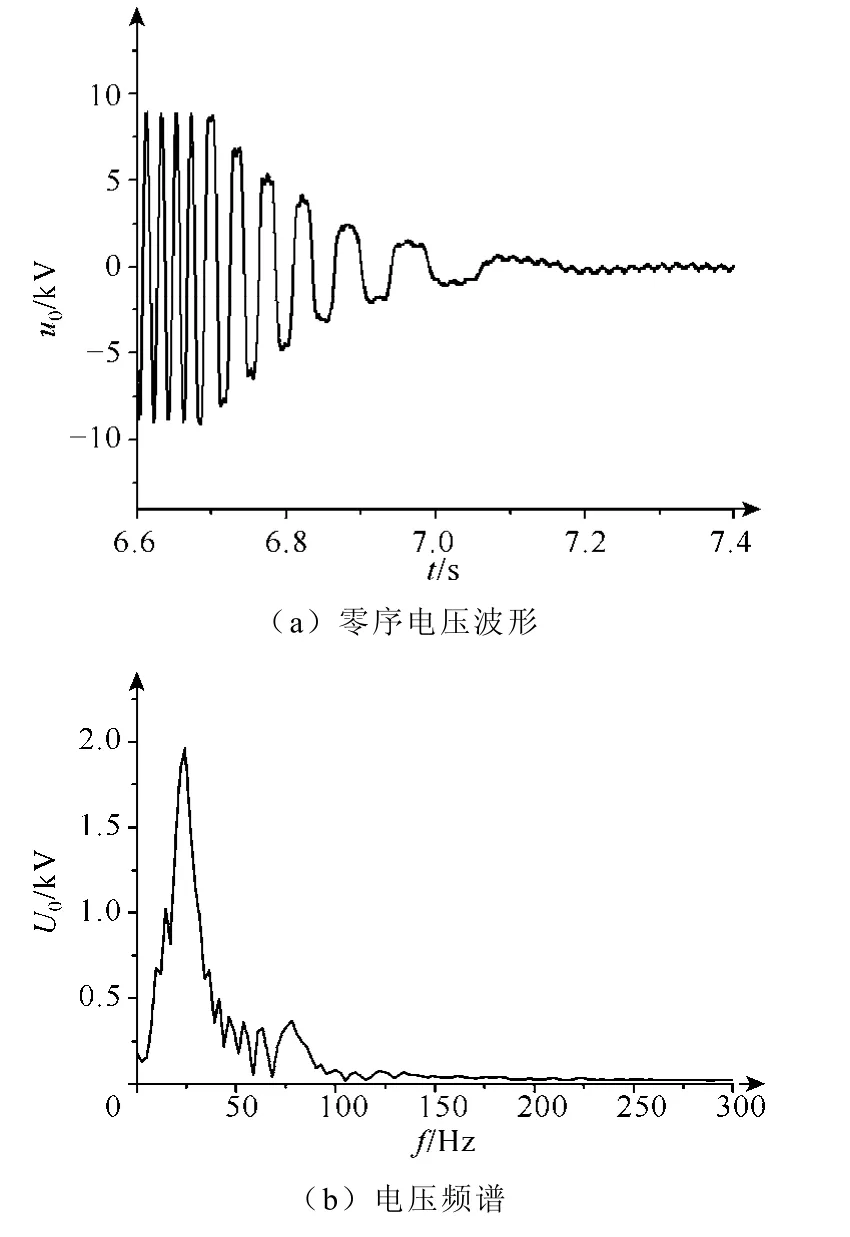
图4 晶闸管不导通时暂态波形Fig.4 The neutral voltage waveform when thyristors are constantly off

3.2 晶闸管导通时零序电压变化

首先考虑晶闸管全导通时这一特殊情况，即相当于消弧线圈二次绕组a1x1短路，由于变压器漏抗远小于滤波回路阻抗，可以忽略滤波回路的影响，配电网零序回路可以等效为消弧线圈漏抗电感L1＋L2与系统对地电容C0构成的LC振荡回路，根据式（3），接地消失时，零序电压按 LC回路自振频率衰减振荡变化，定义fk为晶闸管全导通的状态下的系统的自振频率

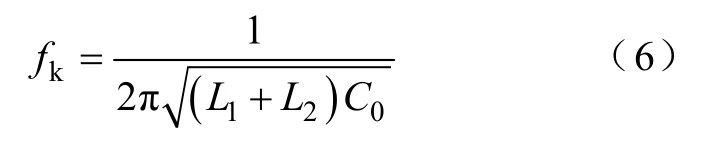
自振周期Tk为

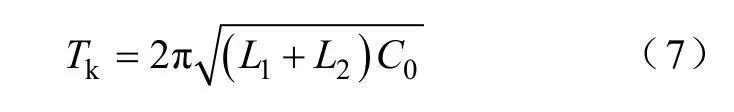
为了研究接地故障消失时，不同的晶闸管导通角度对零序电压的影响，在高压配网模拟试验室中进行了试验研究。试验的消弧线圈型号和基本参数为额定电压:10kV；额定容量:500kV·A；额定电流:82A；阻抗电压:98%。

消弧线圈漏抗电感值为0.224H，由电容器组模拟系统线路的三相对地电容总和为C0=28μF，对应系统电容电流为 53.2A，通过分合接地开关来模拟接地故障解除和产生。

试验中，控制消弧线圈的晶闸管触发延迟角度在接地过程中以及接地消失时都保持在一个固定值，并用示波器记录接地消失暂态过程中零序电压的变化。根据试验时系统电容电流参数，在晶闸管触发延迟角约为 111.6°时接地消失后发生串联谐振，该触发延迟角定义为系统谐振触发延迟角。根据晶闸管触发延迟角的不同，可以将试验分为晶闸管触发延迟角大于、等于和小于系统谐振触发延迟角三种情况。

3.2.1大于谐振触发延迟角时的试验

在试验中晶闸管导通角度保持为142.2°，试验记录的波形如图5所示。图5a表示接地消失时消弧线圈端电压的暂态变化波形，从图 5b电压频谱图中可以看到，零序电压存在3个频率量分别为40.98Hz、50Hz和122.7Hz，其中40.98Hz、122.7Hz是接地故障消失时电压波形衰减振荡产生的频率分量。在晶闸管触发延迟角大于谐振触发延迟角时，零序电压暂态波形的基波频率小于系统电源频率，与触发延迟角大小有关。

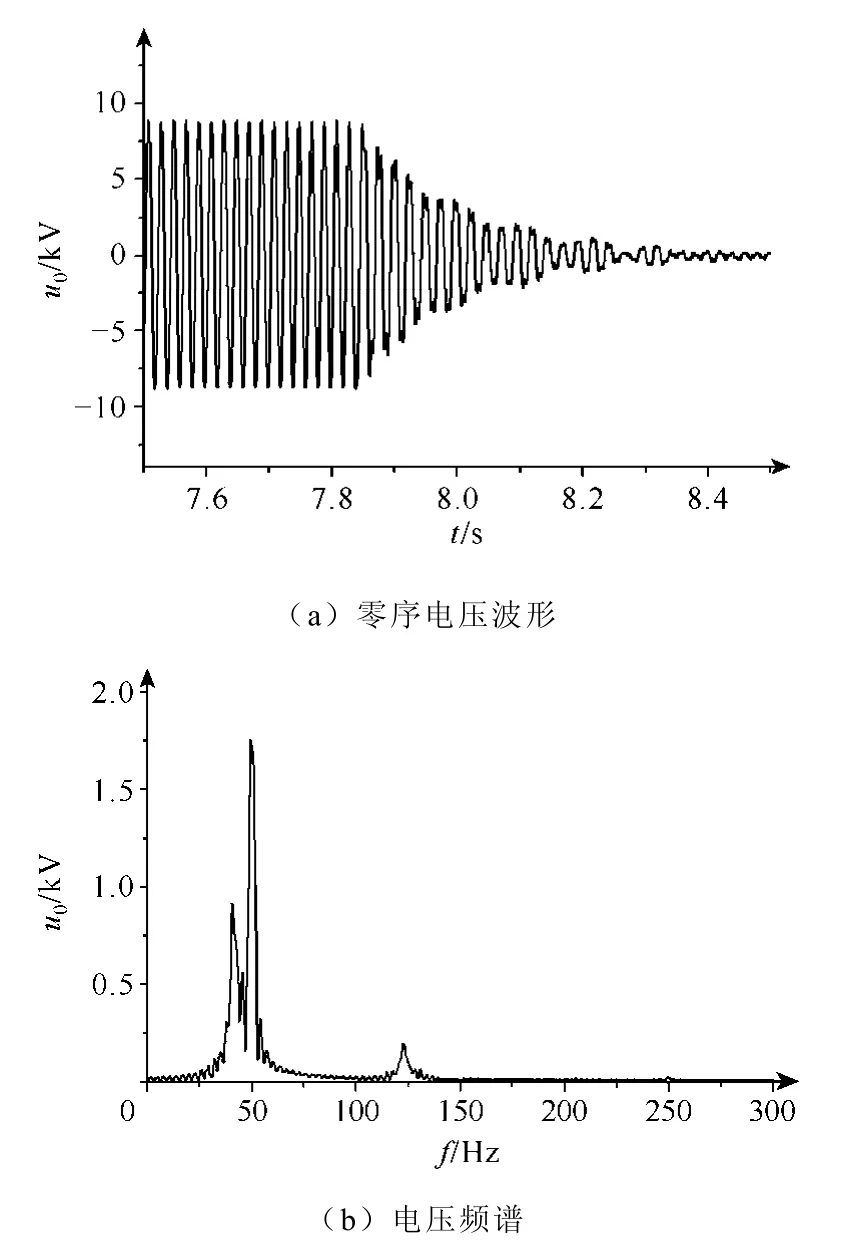
图5 晶闸管导通角142.2º时暂态波形Fig.5 The neutral point voltage when the triggering angle is 142.2º

3.2.2等于谐振触发延迟角时的试验

在试验中晶闸管导通角度保持为112.3º，约等于系统谐振触发延迟角，试验记录的零序电压电流波形如图6所示。图6a表示接地消失时消弧线圈端电压的暂态变化波形，从中可以看出接地消失时零序电压经过一段时间衰减后稳定保持在约 3.1kV，即此时消弧线圈与系统电容发生串联谐振，零序电压没有衰减到零而是从单相接地状态过渡到较高的串联谐振状态。从图6b频谱中看到，试验中零序电压主要频率分量为50Hz，消弧线圈的电流如图6c所示，其频谱主要以 50Hz分量为主，高次谐波电流幅值小。

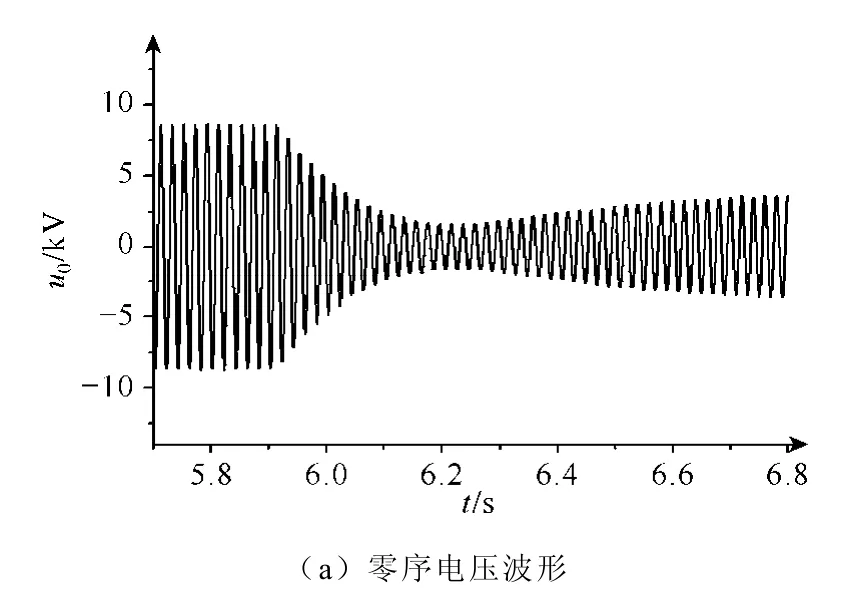
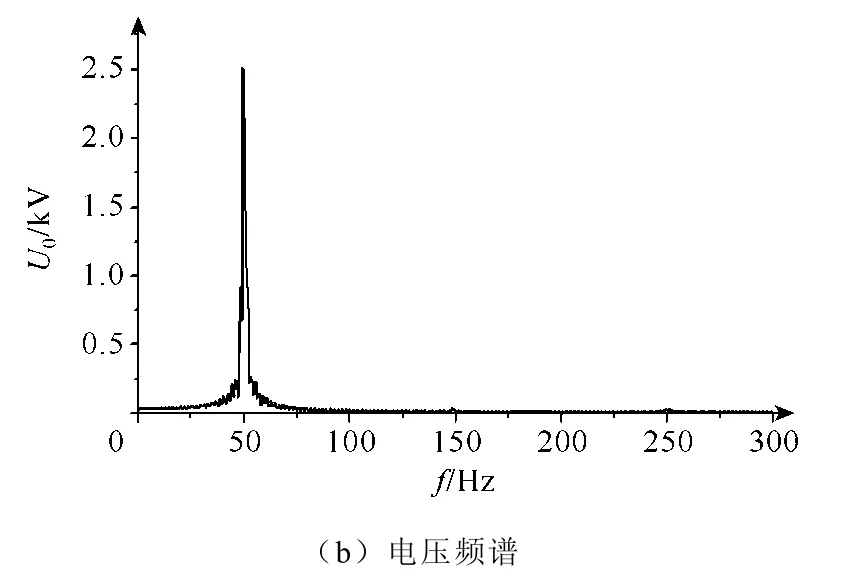
图6 晶闸管导通角112.3º时暂态波形Fig.6 The neutral point voltage when the triggering angle is 112.3º

3.2.3小于谐振触发延迟角时的试验

在试验中晶闸管导通角度保持为 90.4º，试验记录的零序电压电流波形如图7所示。图7a表示接地消失时消弧线圈端电压的暂态变化波形，在单相接地故障过程中，消弧线圈处于过补偿状态。从图7b频谱中看到零序电压主要频率分量为56.2Hz。在晶闸管触发延迟角大于谐振触发延迟角时，零序电压暂态波形的基波频率大于系统电源频率，高次谐波幅值较基波电压非常小，可以忽略。

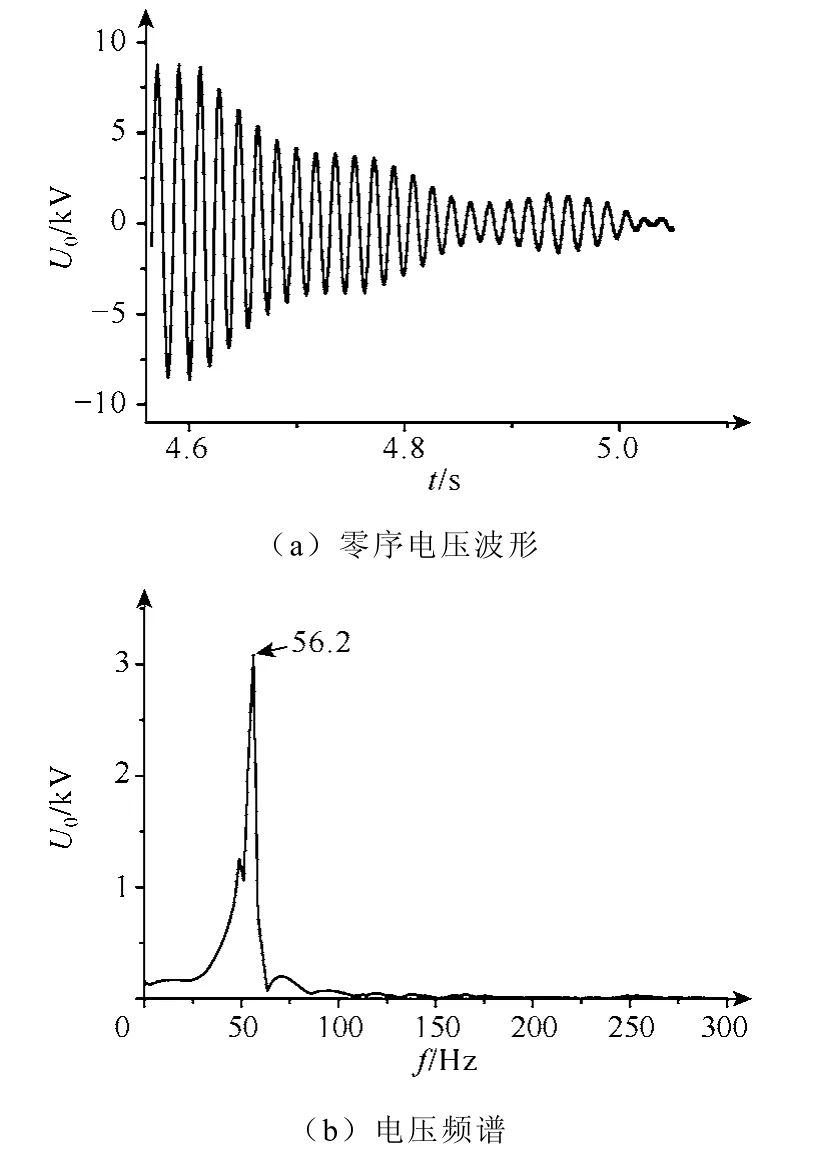
图7 晶闸管导通角90.4º时暂态波形Fig.7 The neutral point voltage when the triggering angle is 90.4º

根据试验结果，配电网接地故障消失时零序暂态电压的基波频率与晶闸管触发延迟角大小有关，调整触发延迟角可以改变零序电压频率，滤波回路阻抗使得零序暂态电压叠加了高频振荡，高频振荡电压幅值远小于基波电压幅值。

3.3 零序电压频率与晶闸管触发延迟角的关系

以下分析推导在接地消失时，高漏抗式消弧线圈的晶闸管导通角度与零序电压频率的关系，其中不考虑系统损耗和消弧线圈损耗的影响。根据 3.1节和3.2节中分析，并忽略滤波回路影响时晶闸管导通和关断情况下影响零序电压u0的因素，图8给出接地消失时u0的波形。

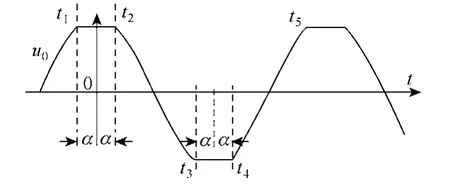
图8 忽略滤波回路影响的零序电压暂态恢复波形Fig.8 The neutral voltage signal in the recovery process with the filter circuit neglected

从t1～t2晶闸管截止，此时零序电压存在多个振荡频率分量，但以低频振荡为主，且高频振荡的幅值很小可以忽略，由于低频振荡频率远小于fk，因而假设晶闸管截止过程中系统对地电容的电压保持不变，即u0(t1)≈u0(t2)；t2时刻晶闸管触发导通，角度α的定义如图8所示，t3时刻晶闸管由于电流过零而截止，从t2～t3，晶闸管处于导通状态，系统对地电容C0通过变压器漏抗电感L1＋L2进行反向充电，因而

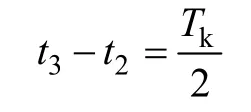
从t3～t4晶闸管截止；t4时刻反向并联的另一晶闸管触发导通，直到t5时刻晶闸管关断截止，同理

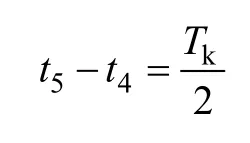
从t1～t5为零序电压一个变化周期，零序电压u0与角度α的关系为

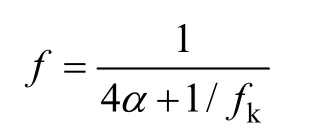
晶闸管的触发延迟角Tα（从电压过零点到触发时刻的延时时间）为，代入上式，得到

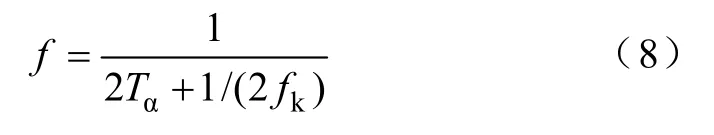
式（8）反映了配电网单相接地消失时零序电压的频率与晶闸管触发延迟角度的关系，说明了高漏抗式消弧线圈暂态过程的一些基本规律。考虑电网损耗以及消弧线圈自身的损耗影响，零序电压波形应是呈逐渐衰减的。对于确定容量的高漏抗消弧线圈其短路阻抗是一定的，而对地电容是在电网正常运行时实时测量获得的，即式中的频率fk是常量，因而式（8）说明了零序电压的频率是晶闸管导通角的单调函数关系。利用高漏抗消弧线圈能够动态调节的特点，在接地消失时改变晶闸管触发延迟角从而引起零序电压频率的变化，根据这一原理提出基于频率跟踪的系统单相接地故障状态识别方法。

在 3.2节中叙述了模拟不同晶闸管导通角条件下的零序暂态电压试验，经过多次试验得到，在接地消失时不同晶闸管导通角度与零序电压的频率关系曲线如图9所示，图中的点线为试验室试验结果，而曲线为根据式（8）的计算结果。从图中可以看到两者基本吻合，试验结果验证了式（8）的准确性，也说明基于频率跟踪的系统单相接地故障状态识别方法的可行性。

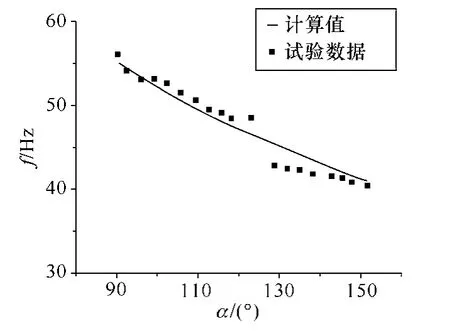
图9 接地消失不同晶闸管导通角度下零序电压的频率曲线Fig.9 The relationship between the neutral point voltage frequency and the triggering time of the thyristors

4 基于频率跟踪的系统单相接地故障状态识别方法

在配电网发生单相接地故障后，高漏抗消弧线圈根据电网电容电流触发晶闸管输出补偿电流，假定此时晶闸管的触发延迟角为Tα1。如果接地故障在某一时刻消失，此时为了判断配电网的接地故障状态是否变化，控制装置将晶闸管的触发延迟角调节到Tα2，根据式（8），零序电压的频率变化Δfm应为

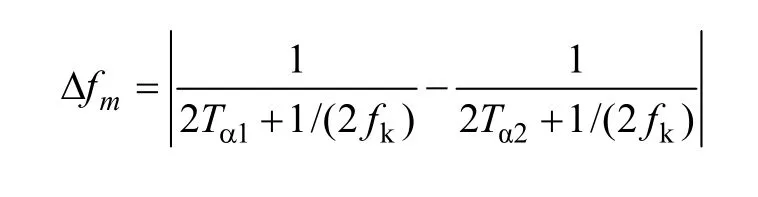
控制装置实际测量零序电压的频率变化为Δf，由于受装置测量误差以及消弧线圈滤波回路的影响，Δf与计算值Δfm有偏差，一般而言，如果

则得出结论，此时接地故障解除，配电网的接地状态发生改变。其中，k为计及误差的系数，通过大量试验得出一般k取0.6即可。如果电网的接地故障没有消失，当控制装置调节晶闸管的触发延迟角度时，由于此时消弧线圈的电压受到故障相电源电压的限制，则零序电压的频率是不变的，即

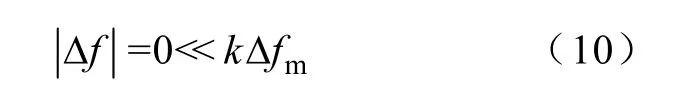
从式（9）和式（10）可以看出，基于频率跟踪的系统单相接地故障状态识别方法判据清晰，判据之间没有交集，从而能够准确判别系统状态的变化。

5 现场应用

基于频率跟踪的系统单相接地故障状态识别方法在试验室验证后，现已应用于现场运行的高漏抗式消弧线圈控制中，下面以某110kV变电站的人工单相接地故障现场试验数据来说明频率跟踪判据的实际应用情况。该110kV变电站10kV侧有两段母线，每段母线上都安装了一套900kV·A的高漏抗式消弧线圈，人工现场单相接地试验是在其中一段母线上进行的，试验进行了金属性接地、弧光接地和高阻接地等不同接地故障方式的接地故障模拟。

图 10为其中一次金属性人工单相接地故障的录波图，其中u0为系统零序电压（即消弧线圈的端电压），I0为消弧线圈电流，Tα为消弧线圈晶闸管的触发延迟角。人工单相接地故障试验时系统的电容电流为 85.5A。从图 10a零序电压波形可以看到，在a点系统接地故障消失，零序电压随之开始衰减，根据控制装置记录的数据，此时晶闸管导通角度为Tα1=111.1º，消弧线圈与系统对地电容处于串联谐振状态，衰减的电压频率约为 50Hz，因而故障点相电压有最低的恢复速度。到b点控制装置开始启动频率跟踪判断，改变了晶闸管的触发延迟角，使得Tα2=149.0º，零序电压频率变为 39.5Hz，符合接地故障状态消失的频率跟踪判据，控制器据此确定此时系统单相接地故障已消除。晶闸管触发延迟角变化避免了消弧线圈与系统对地电容发生串联谐振，同时由于脱谐度的增加使得零序电压加速衰减。到c点零序电压降低至系统允许偏移电压以下时，停止触发可控硅，系统恢复正常运行。

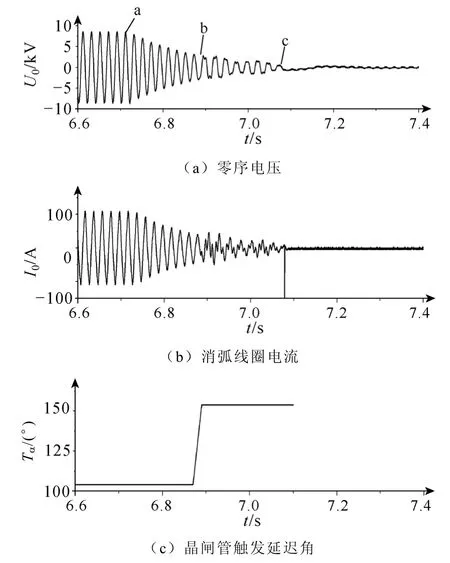
图10 人工单相接地故障的录波图Fig.10 The field test results

现场人工接地试验及实际工程应用情况都说明了基于频率跟踪的系统单相接地故障状态识别方法的可行性，目前该方法已在高漏抗式消弧线圈中广泛应用。

6 结论

本文分析了在应用高漏抗式消弧线圈的配电网中，单相接地故障消失后，配电网中性点电压的暂态变化过程，指出中性点电压与消弧线圈二次可控硅触发延迟角度的对应关系，提出了一种频率判断的方法来识别系统接地状态的变化，即通过改变可控硅的触发延迟角度，由中性点电压的频率与可控硅触发延迟角度对应关系作为判断依据。高漏抗式消弧线圈应用频率判断的方法，能够准确识别接地状态的改变，因而能够避免接地消失后与系统对地电容发生串联谐振，同时无需再采用增大脱谐度的运行方式，因而可以保证在发生接地故障时将接地点残流限制到最小，并且在故障消失后，故障相恢复电压有最慢的恢复速度，防止电弧重燃，充分发挥了谐振接地方式的技术特点。

[1] Petersen W. Limitation of earth current and suppression of earth fault arcs by the earthing coil[J]. ETZ Elektrotechnische Zeitschrift,1919,40.

[2] Griffel D,Leitloff V,Harmand Y,et al. A new deal for safety and quality on MV networks[J]. IEEE Transactions on Power Delivery,1997,12(10): 1428-1433.

[3] Chaari O,Bastard P,Meunier M. Prony’s method: an efficient tool for the analysis of earth fault currents in petersen-coil-protected networks[J]. IEEE Transactions on Power Delivery,1995,10(7): 1234-1241.

[4] Clerlaville J P,Juston Ph,Clement M(EDF). Extinguishing faults without disturbances-compensation coil self-clears three of four faults[J]. Transmission &Distribution World,1997,12(6): 178-181.

[5] Gulachenski E M,Courville E W. New England electric's 39 years of experience with resonant neutral grounding of unit-connected generators[J]. IEEE Transactions on Power Delivery,1991,6(7): 1016-1024.

[6] 吴茜，蔡旭，徐波. 具有两级磁阀的消弧线圈关键参数设计[J]. 电工技术学报,2011,26(10): 224-230.

Wu Xi,Cai Xu,Xu Bo. Design of key parameters about two-stage magnetic valve arc suppression coil[J]. Transactions of China Electrotechnical Society,2011,26(10): 224-230.

[7] 盛建科,陈乔夫,熊娅俐,等. 基于磁通可控的新型自动调谐消弧线圈[J]. 电工技术学报,2005,24(3): 76-81.

Sheng Jianke,Chen Qiaofu,Xiong Yali,et al. A new type automatic resonant arc-suppressing coil based on controllable magnetic flux[J]. Transactions of China Electrotechnical Society,2005,24(3): 76-81.

[8] Lu Guoqing,Jiang Xinyu,Ouyang Xudong,et al. A new type of compensation coil at the neutral-point of distribution system[C]. 2000 Proceedings of the China International Conference on Electricity Distribution,2000,10: 43-45.

[9] Lu Guoqing,Jiang Xinyu,Yang Xu,et al. A study on an ideal operation mode of fast arc-suppressing and fast grounded line locating for neutral grounding in distribution network[C]. 2006 Proceedings of the China International Conference on Electricity Distribution,2006,9: 70-76.

[10] Zivanovic R,Schegner P,Seifert O,et al. Identification of the resonant-grounded system para- meters by evaluating fault measurement records[J]. IEEE Transactions on Power Delivery,2004,19(7): 1085-1090.

[11] 李玲玲,孙鹤旭,王晓宏. 谐振接地电力网自动调谐的新方法[J]. 中国电机工程学报,2003,23(6):77-80.

Li Lingling,Sun Hexu,Wang Xiaohong. A new automatic tuning method for resonance grounding power network[J]. Proceedings of the CSEE,2003,23(6): 77-80.

[12] 江渝,刘和平,冉立,等. 连续调节消弧线圈接地系统单相接地故障谐振状态在线监测的研究[J]. 中国电机工程学报,2005,25(13): 36-40.

Jiang Yu，Liu Heping，Ran Li,et al. Study on the judgement of resonance state during the single-phase ground in the distribution with the continuously adjustable ASC[J]. Proceedings of the CSEE,2005,25(13): 36-40.

[13] 要焕年,曹梅月. 电力系统谐振接地[M]. 北京:中国电力出版社,2009.