考虑互感器传变特性的输电线路暂态保护雷击干扰与线路故障识别方法

束洪春 曹璞璘 杨竞及 董 俊 田鑫萃

（1．昆明理工大学电气工程学院 昆明 650500 2．云南民族大学 昆明 650500 3．哈尔滨工业大学电气工程及自动化学院 哈尔滨 150001）

1 引言

行波保护与暂态量保护等基于瞬时值的高速保护具有动作速度快、不受系统振荡和CT饱和影响等优点[1,2]，因此自行波保护与暂态量保护概念提出以来就受到广泛关注[3,4]，目前，已有文献报道基于行波保护原理的行波方向继电器应用于实际线路上[5]。然而此类基于故障暂态信号的保护原理所需采样率较高（至少数十kHz），不可避免地会受到断路器分合闸、雷击干扰等冲击的影响，一定程度上降低了保护的可靠性。

在超（特）高压系统中，由于线路耐雷水平较高，雷击线路或杆塔而未造成闪络故障的情况时有发生，在实际工程中线路保护基本都是工频保护，其算法是基于工频量进行计算，且大都带有低通滤波器，不会受到雷击干扰的影响，但是行波保护与暂态量保护是基于短时窗内瞬时值进行保护算法构建，雷击干扰的冲击可能会被误判为故障发生，引起保护误动作。为避免雷击未闪络导致的干扰引起行波保护与暂态保护误动，国内外学者对雷击干扰识别方法进行了大量研究[6-14]，文献[8-11]分析了雷击干扰与故障在不同频带暂态能量分布不同的特点，并分别利用小波、Fourier变换和S变换等方法刻画暂态能量频域分布进而判断雷击干扰与故障，但是不同频带能量分布会受到故障、雷击距离和雷电流大小的影响，阈值不易整定。文献[12,13]分别构造了波形一致性系数与时间轴两侧电流波形面积比进行雷击干扰与故障电流判别，其本质是利用了雷击干扰情况下故障分量会逐渐趋于 0，而故障情况下故障分量会包含较大的短路故障工频量，此类方法在一定程度上会受到故障初相角的影响。文献[14]针对直流线路提出了基于多判据可拓融合的判别方法，但是该方法在交流线路上的可行性有待考证。上述方法大多是采用电流对雷击干扰与故障进行识别，但是与发电厂相联的升压变电站往往只有一回出线，电流行波浪涌不够明显，不适用于行波检测，而学术界对电容式电压互感器（CVT）能否准确在二次侧反映行波一直存在争议，故缺乏基于CVT二次侧数据的雷击干扰判别方法。本文依据实测CVT与CT宽频传输特性，利用矢量拟合法和网络综合方法，建立了CVT与CT宽频传输模型，在数字仿真过程中CVT二次侧输出既包含CVT传递函数极点引起的振荡，也包含数值计算过程中引起的数值振荡，分析了CVT二次侧传递对行波识别的影响。以CVT与CT二次侧输出波形对雷击故障、非雷击性故障与雷击干扰进行 PCA聚类分析，由于故障与雷击干扰暂态波形包含的波形特征不同，而同一类型的暂态波形中具有较为相似的波形特征，将不同故障类型的样本数据投影到PCA坐标系上，通过支持向量机（Support Vector Machine，SVM）对PCA坐标系上的点簇进行区分，形成PCA-SVM机器学习判别机制，对故障与雷击干扰进行区分。

2 雷击对线路保护的影响分析

2.1 工频保护

传统的工频保护算法是基于提取得到的工频量进行计算，虽然工频量保护的采样率较低（通常仅为 1.2kHz），且为了避免故障或扰动产生的高频量对工频保护算法造成不利影响，工频保护装置通常会带有低通滤波元件[15]，雷击干扰引起的高频量难以被采样环节捕捉到。即使低通滤波元件未能完全滤除高频量，在保护算法实现环节进行的工频量提取也能够有效剔除高频量影响，故雷击干扰对工频保护的影响基本可以忽略。

2.2 行波保护

行波保护是利用故障发生后极短时间内的行波波头特征反映故障发生与否，故通常需要高于500kHz采样率捕捉行波波头。雷击干扰与雷击故障产生的初始行波波头都是由雷电注入或感应产生，波头特征极为相似，难以辨识，雷击干扰产生的行波会被行波保护误认为故障行波，导致保护误启动。因此，为避免行波保护受到雷击干扰的影响，需要特殊算法对故障与雷击干扰进行判别。

2.3 暂态量保护

暂态量保护通常是利用短时窗内行波传播方向、电气量变化速率或高频能量大小[4,16]等特征反映故障发生，与行波保护相比，暂态量保护所需采样率较低（通常为数 kHz至数百 kHz），但是暂态量保护亦是直接对瞬时值进行计算，而雷击干扰包含大量高频能量，会引起电气量短时窗内的剧烈变化，可能导致保护将雷击干扰误判为故障，故暂态量保护也需要对故障与雷击干扰进行判别。

3 故障与雷击干扰的电磁暂态分析

3.1 非雷击性故障

线路发生非雷击性故障情况下，系统仅受到故障激励源接入的冲击，设Zf(s)为故障激励源等效电阻，则在量测端M，故障初始电流行波浪涌可以表示为

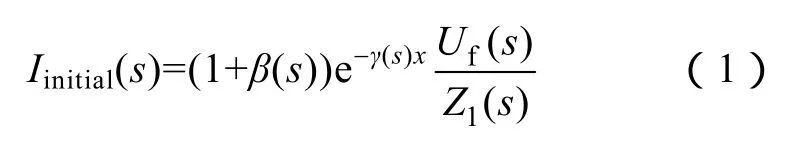
式中，故障时刻产生的电压行波浪涌幅值为Uf(s)；γ(s)为线路传播常数；母线处反射系数β(s)为

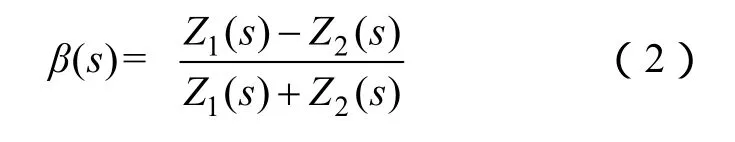
式中，Z1(s)表示故障线路的波阻抗；Z2(s)表示母线上所有健全线路、母线杂散电容和变压器等表现出的等效波阻抗；β(s)的大小主要与母线出线形式有关。

3.2 雷击故障

雷击故障情况下，由于绝缘子两端电势差大于击穿电压需要一个电势差建立的过程，故雷击与绝缘子闪络之间存在一个时间差，线路传输系统会先后受到雷电流激励和故障激励源接入两次冲击。设Ilightning(s)为注入导线的雷电流或雷击塔顶、避雷线时在线路上感应产生的电流，τ为雷电冲击发生与绝缘子击穿之间的时间差，则在量测端M，雷击故障引起的初始电流行波浪涌可以表示为

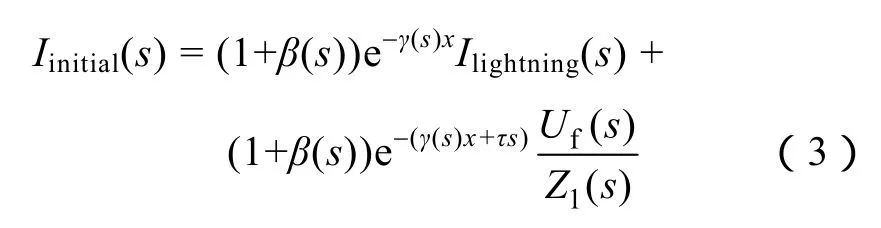
由于绕击故障初始行波中包含注入导线的雷电流成分，故在线路两端观测到的初始行波浪涌包含部分雷电流行波。

3.3 雷击干扰

雷击干扰情况下，绝缘子未被击穿，线路上的行波仅包含注入导线的雷电流或雷击引起的感应电压，线路上仅包含雷击引起的行波浪涌，线路M端观测到的初始行波浪涌可以表示为

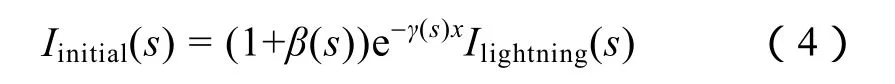
由上述分析可知，无论是雷击故障还是非雷击性故障，线路两端量测点所测行波信号中都包含故障激励源造成的行波响应，且故障激励源会长时间存在，引起工频量的变化，而发生雷击干扰的情况下，线路上只能观测到雷电流激励引起的行波，工频量的注入是雷击故障与雷击干扰的根本区别。

在式（1）～式（3）中，β为母线处的电流反射系数，其大小会受到母线出线数量的影响。假设母线上各条线路的波阻抗相等，n为母线上出线总数，不考虑母线杂散电容的影响，则母线处电流和电压的反射系数可以分别表示为

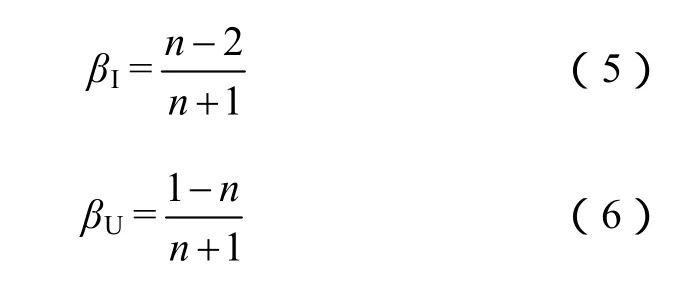
当母线出线数大于2时，电流行波反射系数βI＞0，电压行波反射系数βU＜0，当反射系数为正时，反射波与入射波极性相同，母线处观测到的行波浪涌更为明显，当反射系数为负时，反射波与入射波极性相反，行波浪涌幅值降低，不易观测。当母线上仅有一回出线的极端情况下，βI=-1，βU=1。在实际中，500kV基本上都采用 3/2接线形式，母线出线数通常大于2，电流行波能够较好地反映行波浪涌引起的波形突变。但是电厂侧的出线数往往仅为1条，电流行波浪涌不够明显，而电压行波浪涌容易检测。综上所述，线路两端所测行波幅值会受到母线出线数量的影响，选择电压或电流进行行波监测需要考虑母线出线数量的影响。

4 故障与雷击干扰识别方法

4.1 瞬时功率

从线模电压和电流、零模电压和电流、相电压和电流上都能够观察到雷击干扰与接地故障引起的波形变化，故选取合适的电气量尽可能突出故障与雷击干扰的特征以便于区分故障与雷击干扰非常重要，同时又需尽可能降低参与运算的观测量个数，避免需要从多个观测量中进行选取而引起计算量增加。

无论是 Clarke变换、Karenbauer变换还是Wedpohl变换，都存在单一线模量不能反映所有故障类型的缺点，需选取至少两类线模量才能适应所有的故障类型，文献[17]所提出的相模变换方法虽然能够在单一线模量下反映出所有故障类型，但是在同一类型的故障情况下，故障相的不同将导致此模量上反映出的行波幅值有较大差异，不利于故障波形特征的定量提取。若采用相电压或相电流进行检测，则应选取其中一相的电压或电流，以避免同时检测三相电气量造成不必要的数据量和计算量增加，但是不同故障类型下三相电气量上表现出的故障特征存在差异，因此需选出故障特征最明显的一相，导致必须有选相算法配合才能实现。

零模通道反映的是线路与大地之间的回路，行波在零模通道中衰减和畸变较为严重[18]，不利于反映故障特征。发生单相接地故障或雷击导线未闪络时，健全相和故障相、遭雷击相的波形突变方向相反，而零模量在数学表达上表现为三相电气量相加，削弱了故障相表现出的故障特征。

根据上述分析，构造三相瞬时总功率Δp

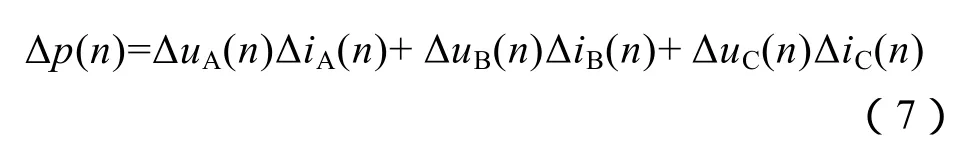
式中，Δuk(n)和Δik(n)（k=A，B，C）分别为三相电压、电流的故障分量。在被保护线路发生故障或雷击干扰时，线路两端所测初始电压行波浪涌与初始电流行波浪涌极性相反，因此对于初始行波浪涌

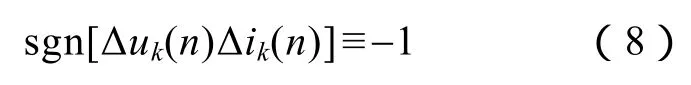
故三相 Δuk(n)Δik(n)的初始行波浪涌极性恒为负，避免了三相电气量直接相加造成的故障相或遭雷击相暂态特征被削弱的问题。

4.2 主成分分析聚类方法

主成分分析（PCA）是最为常见的多变量分析手段之一，最早由Pearson在1901年提出[19,20]，其主要思想是通过对多变量观测值进行变换，得到多组不相关的独立变量，并在对新的独立变量进行降维的同时保留尽可能多的原始观测值信息。

假设n个数据都可用p个变量进行描述，从而构成观测矩阵X，其形式为

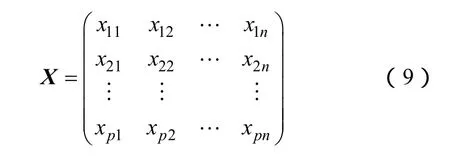
假设矩阵V满足VTV=1，则主成分分析就是利用变换矩阵VT对原矩阵X进行线性变换，形成新的矩阵Y，即

设yi为矩阵Y中第i维行向量，y1为第一主成分，且

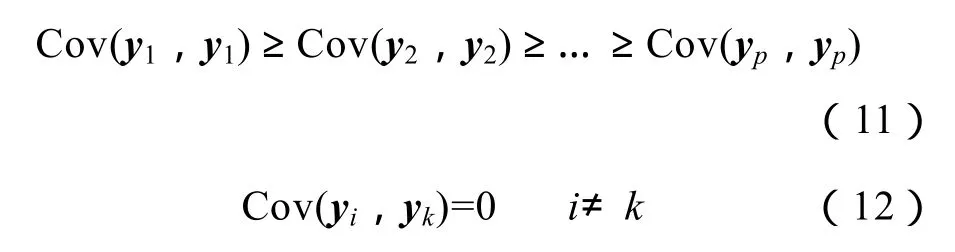
式中，Cov为计算两变量协方差。

可见，主成分分析的过程也就是坐标旋转的过程，新坐标系中各坐标轴的方向就是原始数据方差最大的方向。设主成分分析后得到的新坐标为[PC1,PC2,…,PCp]，具有相似特征的数据在 PC1、PC2等低阶坐标下应能聚集成簇，实现聚类。

4.3 支持向量机

支持向量机（SVM）可以将线性不可分的样本通过核函数映射到高维线性可分空间[21,22]，以实现数据样本的分类。将待划分的输入样本记为Rn，经过非线性核函数Φ的作用映射到高维线性可分的空间Fn，即

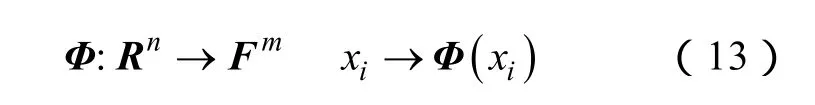
式中，Φ为核函数。本文选用的核函数为高斯径向基核函数（RBF），RBF核函数具有较好学习能力，无论是低维、高维、小样本还是大样本情况，RBF核函数均适用，且具有较宽的收敛域，是较为理想的分类依据函数。

将高维空间可分的样本经过函数f的作用，使得输入样本分成两类，且使分类间隔最大，即

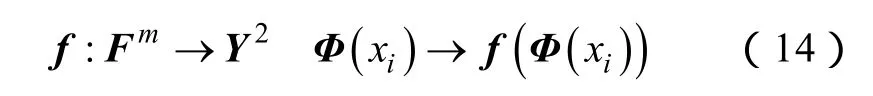
两类样本中离分类面最近的投影点将构成平行于超平面的向量H1、H2，H1、H2就叫做支持向量，设w为权重向量，b为偏置项，则超平面上H1和H2之间的距离为

最优分类面问题可以表示成约束优化问题，即求取最大的m。转换成优化问题为

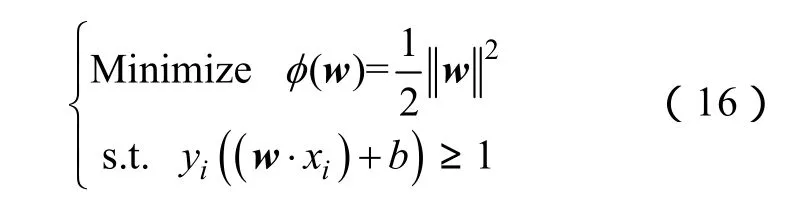
5 CVT与CT暂态特性

在国内，220～500kV等级的线路大都选用电容式电压互感器（CVT）进行电压测量，在110kV及以下的线路上，CVT亦有逐渐替代电磁式电压互感器的趋势。一直以来，CVT的暂态传变特性是否影响行波在二次侧的准确获取饱受争议，有观点认为CVT的暂态传变特性不好，对行波和暂态量等高频量的传递存在严重失真，不适于采用电压研究行波测距和行波保护。也有研究依照国外文献搭建了CVT物理模型，利用 CVT二次侧输出进行行波测距，并得到了较好的测试效果[23,24]。

本文利用文献[25]实际测量得到CVT和CT宽频传输特性，以矢量拟合法对测量结果进行有理逼近，将测量得到的频域响应表示为一阶有理分式之和的形式，通过网络综合方法，利用矢量拟合得到的频域响应表达式建立对应的互感器等效电路模型。

5.1 散射参数测量

用散射参数表示的二端口网络如图1所示，电压入射波a1在端口1输入，在端口1反射系数是s11，到端口2的透射系数为s12；电压入射波a2在端口2输入，在端口2反射系数是s22，到端口1的透射系数为s21。离开端口 1的电压波b1，是a1在端口 1的反射波与端口2的电压入射波a2的透射波之和；离开端口 2的电压波b2，是a1的透射波与a2的反射波之和。

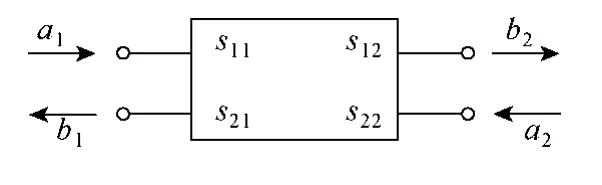
图1 二端口网络散射参数Fig.1 Two-port network scattering parameters

根据文献[25]，测量得到的CVT散射参数可以经公式转换得到阻抗参数矩阵。由开路阻抗矩阵Z得到互感器的T形等效电路如图2所示，其中，Z1=z11-z12，Z2=z22-z12，Z0=z12-z21。

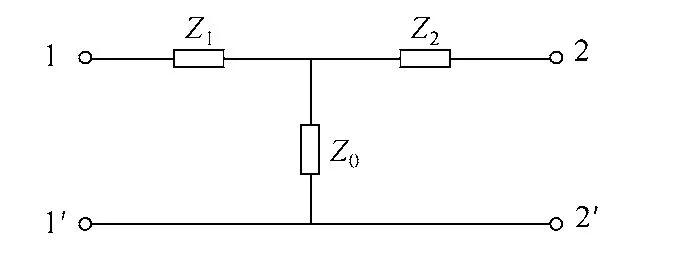
图2 互感器T形等效电路Fig.2 T-type equivalent circuit of transformer

5.2 矢量拟合法

为建立比较精确的互感器宽频等效模型，可以利用矢量拟合法对互感器的变比、端口阻抗（导纳）等参数的频率特性进行有效的数学拟合，进而得到这些频率特性的有理逼近函数表达式。

采用矢量拟合法时，拟合函数表现为部分分式之和的形式，即

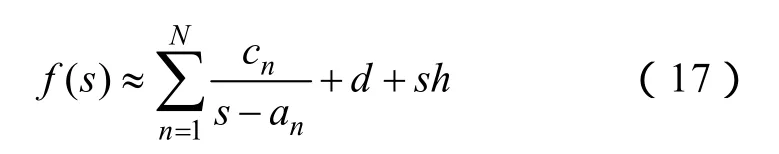
式中，极点an及其对应的留数cn既可以为实数，也可以为共轭复数；d和h均为实数；N为极点总数。矢量拟合法预先设定一组初始极点，通过反复迭代来求取精确的an，迭代过程归纳如下：

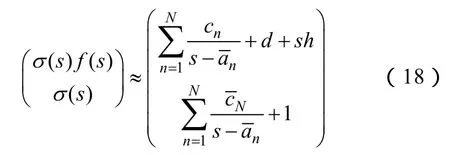
式中，σ(s)与σ(s)f(s)的有理函数表达式具有相同的极点。并且，σ(s)在极高频段被强制收敛为1，从而解决了σ(s)求解过程中出现的数值性问题。

将σ(s)的有理函数表达式代入式（18），可得

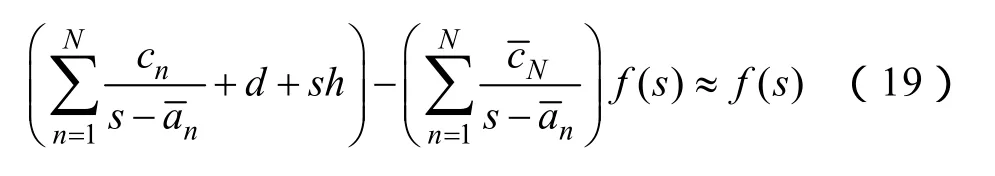
式（19）为关于未知数cn(s)、d、h和的线性方程组，将各频率点的s、f(s)值代入式（19）可得到一组超定线性方程组

其中

应用最小二乘法求取式（21）中的cN、d、h和，可得

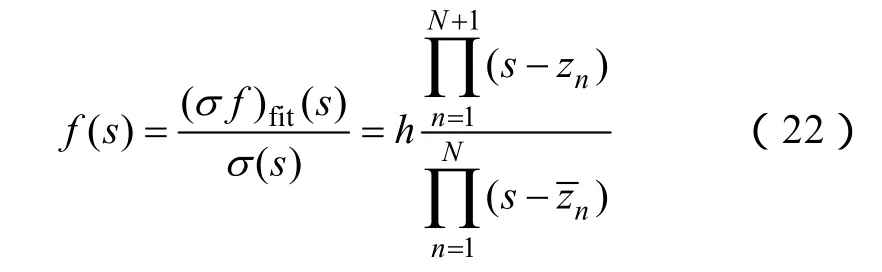
由式（22）可知，f(s)的极点等于σ(s)的零点。因此，通过计算σ(s)的零点就可以得到一组较为精确的f(s)的极点，将初始极点代入式（22）进行迭代运算，求取式（21）中的未知量。当方程达到收敛时，σ(s)的值为 1，即所有的值为 0。将矢量拟合法用于互感器的频率特性时，一般可以忽略式（17）中sh这一项，利用矢量拟合方法对文献[25]给出的CVT和CT的T形等效电路阻抗Z1、Z2、Z0分别进行有理逼近，拟合结果如附图所示。

5.3 互感器阻抗频率特性等效与建模

通过网络综合分析中的滤波器综合方法，可以通过矢量拟合法所得频率特性与散射参数建立满足互感器频率特性的等效电路[26]。

假设在复平面左半平面有N-2K个实数极点和K对共轭复数极点，且设K对共轭复数极点为

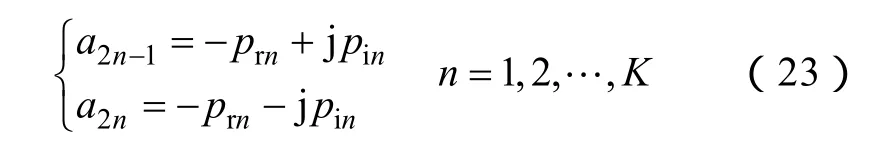
其中，prn＞0，共轭复数极点对应留数为

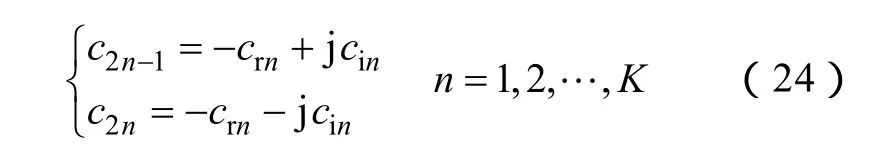
设N-2K个实数极点为an＜0，其对应的留数为cn，n=2K+1,…,N；由以上假设可以得到

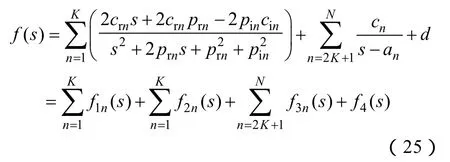
其中

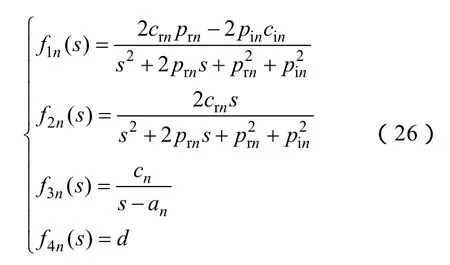
可通过网络综合方法，根据附表内容对式（26）分别建立f1n(s)、f2n(s)、f3n(s)和f4n(s)对应的电路模型，获得CVT与CT的等效电路模型。

5.4 数值振荡分析

由附图可知，在20kHz和500kHz附近，CVT幅频特性存在频率响应极点，当一次电压包含这两种频率成分时，二次电压中会出现相应振荡分量。但是在利用数值计算方法计算 CVT二次侧输出的过程中，数值计算引起的数值振荡无法避免，故利用数值仿真技术计算得到的 CVT二次侧输出包含两部分振荡，一部分源自CVT自身传递函数中的极点，另一部分则源自数值求解产生的数值振荡。

图3和图4分别展示了梯形法、龙格库塔法及改进欧拉法等不同类型的电磁暂态数值计算方法所得CVT二次侧电压波形。

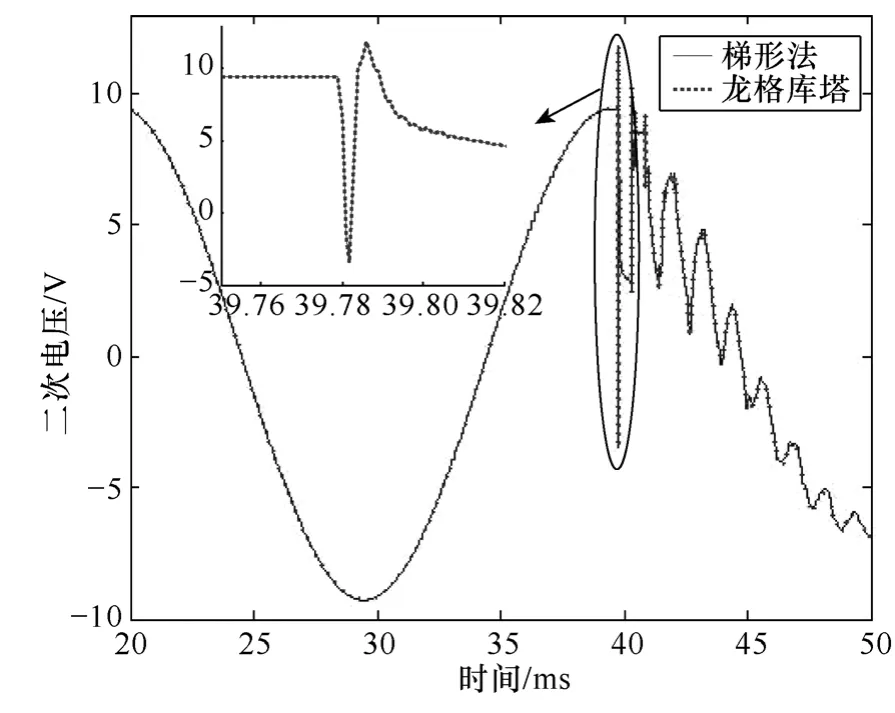
图3 梯形法和龙格库塔法Fig.3 Comparison between trapezoidal rule and Runge-Kutta method

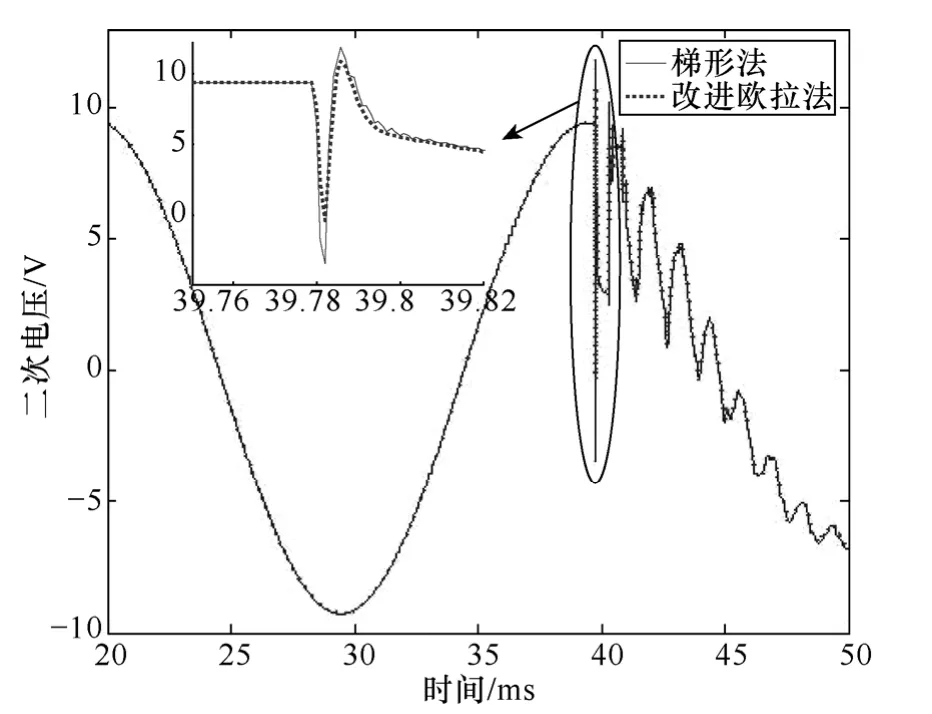
图4 梯形法和改进欧拉法Fig.4 Comparison between Trapezoidal rule and improved Euler method

由图3和图4可知，不同的数值计算方法都会引入附加振荡，在数字仿真实验中的CVT二次侧输出不仅包含CVT模型极点造成的附加振荡，也包含数值计算方法带来的附加振荡。数值计算方法引入的附加振荡会造成 CVT二次侧输出包含虚假的频率成分，可能导致CVT二次侧输出波形中包含不真实的振荡。

由数值计算引起的数值振荡虽然不可避免，但是数值振荡引起的振荡幅值较小，对行波浪涌引起的波形突变影响很小，对于行波的检测和标定不会带来太大影响。

6 仿真分析及结果

6.1 仿真建模

以图5所示的仿真系统为例，线路全长150km，采样率为1MHz，沿输电线路MN每隔1km分别设置雷击避雷线A相闪络、雷电绕击A相闪络、A相90°金属性接地故障、雷击避雷线干扰和雷电绕击 A相干扰5种情况，对此进行电磁暂态仿真遍历，并将二次侧数据归算至一次侧，以便于比较。杆塔与线路模型如图7所示，杆塔使用多波阻抗模型进行模拟，输电线路为四分裂导线，雷电流模型选用双指数模型，绝缘子伏秒特性曲线由下式确定

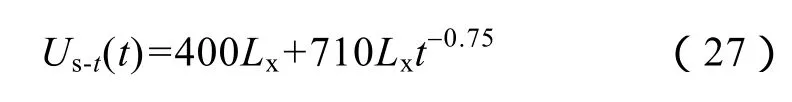
式中，t为雷击开始到闪络所经历的时间，单位为μs；Lx为绝缘子串长度，本文中绝缘子长度选为5.46m[27]。考虑冲击电晕对雷击波形的影响，根据文献[28]所述搭建冲击电晕等效电路，在此不再赘述。

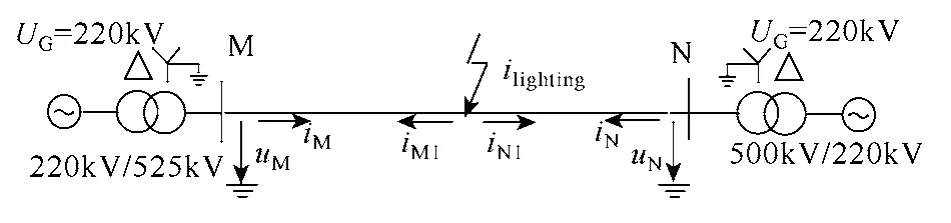
图5 500kV线路模型示意图Fig.5 Simulation model of 500kV transmission lines

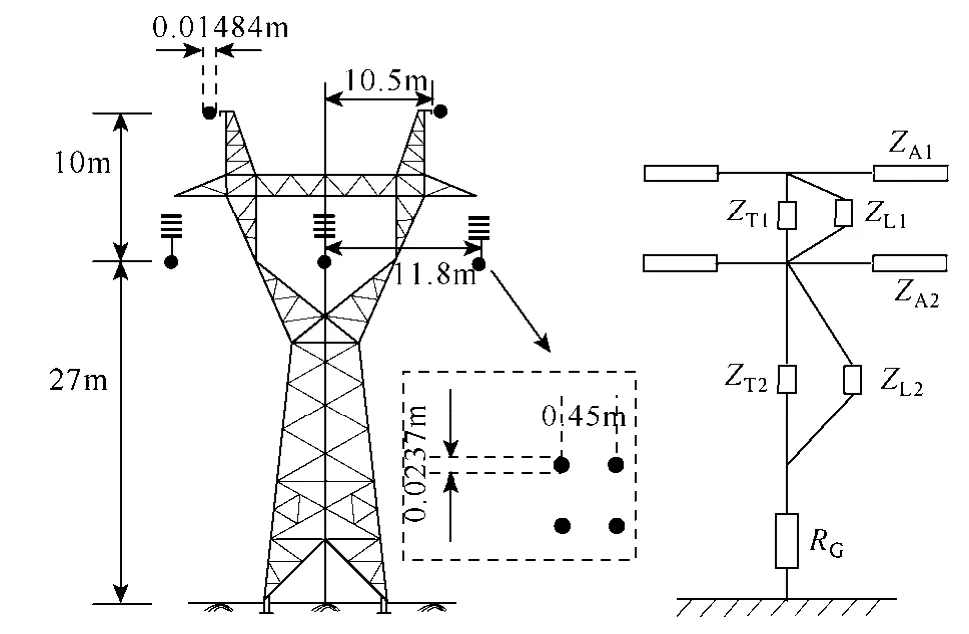
图6 500kV杆塔模型Fig.6 500kV tower model

6.2 CVT与CT传变特性对行波波头辨识的影响

CVT自身的频率特性存在极点，在频谱范围较宽的行波时，极易在二次侧输出中引入频率特性极点引起的附加振荡，故必须从二次侧与一次侧的波形比较入手，分析附加振荡是否会影响行波浪涌检测与识别。

根据图5所示仿真模型，设距离M点40km处发生A相金属接地故障，将二次侧数据归算至一次侧，M点一次侧与二次侧电压、电流波形如图7所示。

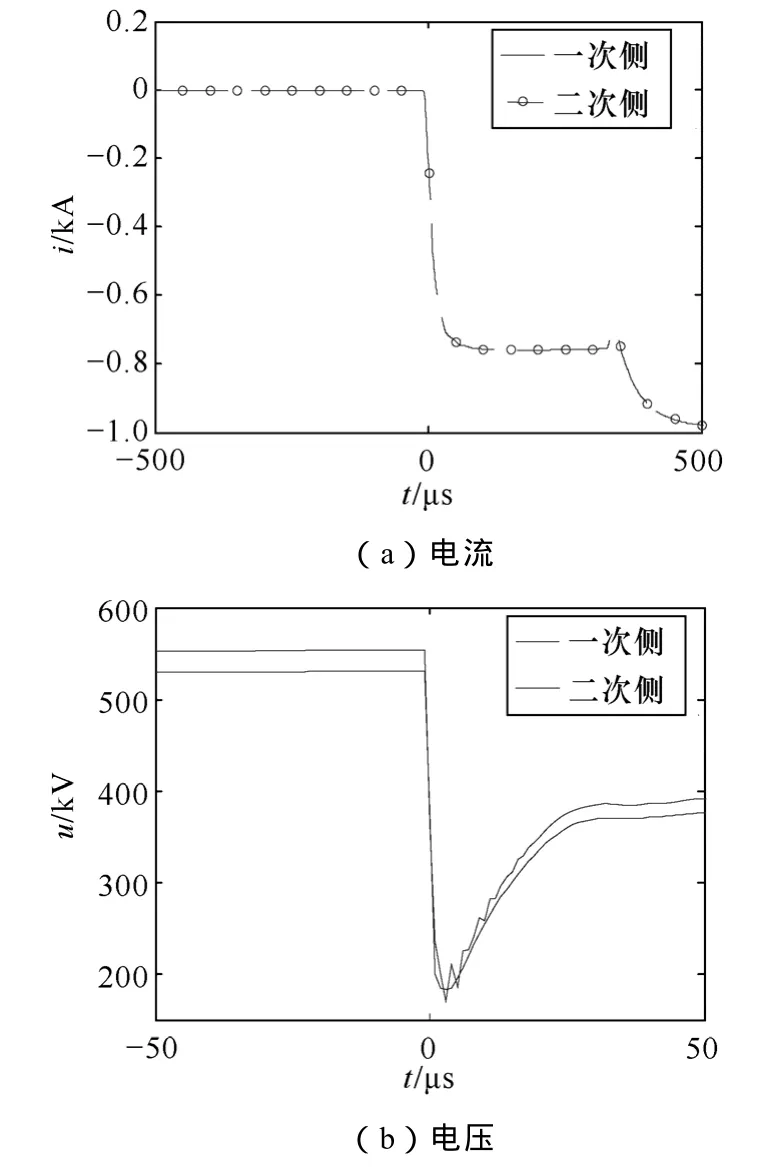
图7 一次侧与二次侧电压、电流比较Fig.7 Voltage and current of input and secondary output

由图7可知，CT传变特性对电流行波的辨识并无太大影响，在 1MHz频率范围内，CT能够较为真实地反映行波特征，一次侧与二次侧波形相差很小。而在CVT输出中，附加振荡伴随行波的到达而产生，在初始行波后出现多个由附加振荡产生的奇异点，但是奇异点的幅值与初始行波相比非常小，且附加振荡不会超前于行波浪涌产生，不会影响行波的检测与识别。

6.3 仿真结果

根据图5所示仿真模型对以下5种雷击或故障情况进行仿真：

（1）雷击避雷线导致 A相闪络，雷电流幅值150kA，故障角60°。

（2）雷电绕击 A相闪络，雷电流幅值 40kA，故障角30°。

（3）A相接地故障，为提高普通接地故障与雷击的相似性，过渡电阻设为0，故障角90°。

（4）雷击避雷线干扰，雷电流幅值60kA。

（5）雷击A相导线干扰，雷电流幅值10kA。

利用仿真得到的电压、电流计算瞬时功率Δp(t)，五种情况的Δp(t)波形曲线簇图8所示。取各瞬时功率曲线簇到达量测端前100个采样点，到达量测端900个采样点共1ms时窗数据进行PCA聚类，得到其在PCA空间中的投影值q1、q2分布如图9所示。

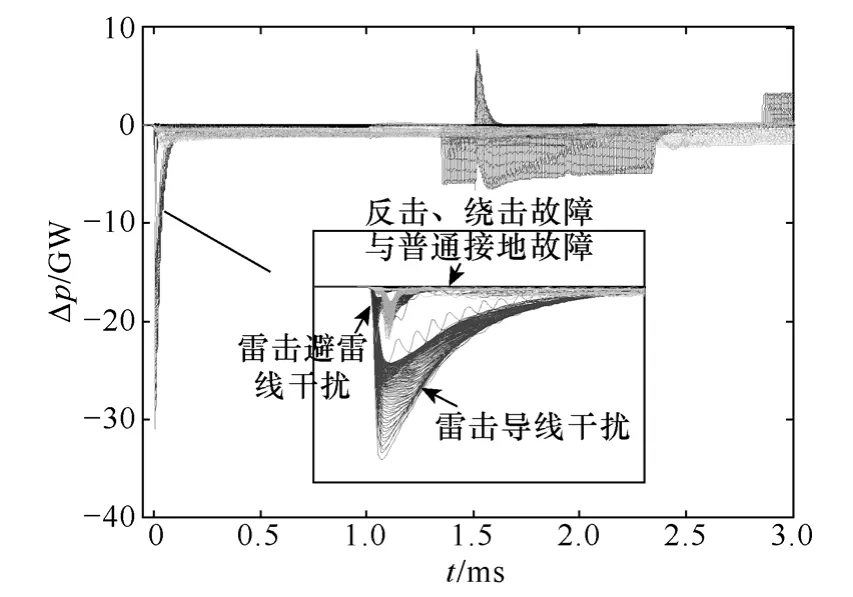
图8 故障与雷击干扰情况瞬时功率波形曲线簇Fig.8 Instantaneous power curve cluster of faults and lightning disturbance

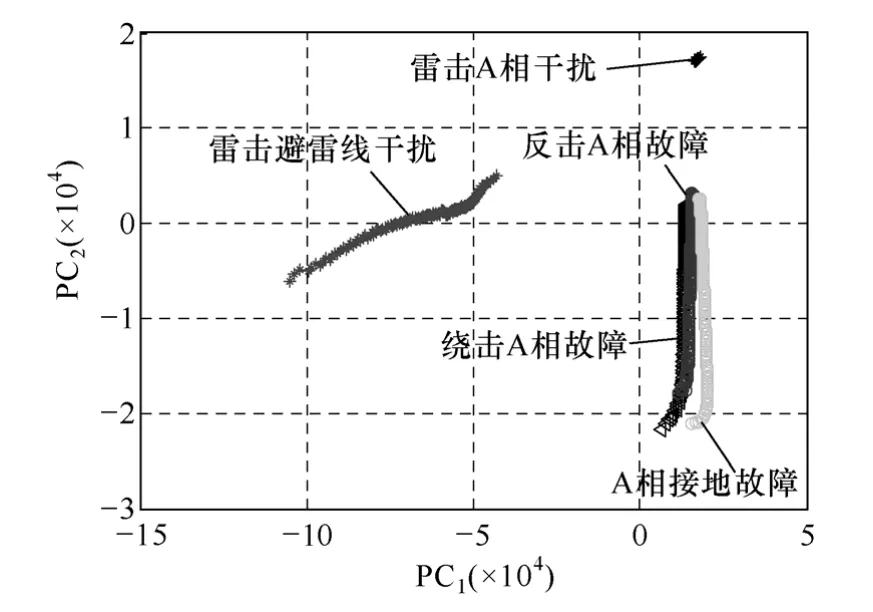
图9 PCA空间分布Fig.9 Distribution of data on PCA space

由图9可以看出，由二次侧数据计算得到的故障与雷击干扰瞬时功率曲线簇在 PCA空间中分别聚类成3条点簇，可根据瞬时功率在PCA空间中的分布情况，来判别雷击干扰和故障。

将五种情况下的瞬时功率曲线簇进行 PCA聚类分析，得到其第一主成分q1和第二主成分投影值q2作为SVM的输入属性，选取径向基函数（Gaussian Radial Basis Function）作为核函数，若输出为1，则判断为故障，若输出为 0，则判断为雷击干扰。现每次对一条新的样本做测试，测试样本在PCA空间中的分布如图10所示，样本设置和SVM输出结果见下表。

综上所述，利用 PCA聚类方法将故障与雷击干扰的数据投影至 PCA第一主成分与第二主成分组成的坐标系上，可以将故障与雷击干扰聚类至不同的点簇中心附近。使用SVM对PCA投影坐标系上的投影点进行分类，能够准确划分故障与雷击干扰。

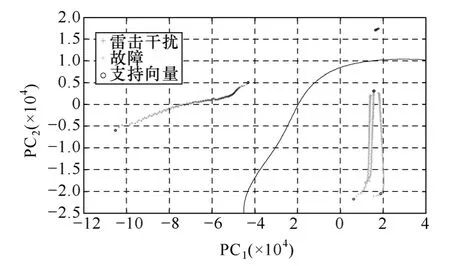
图10 PCA-SVM机器学习判别机制Fig.10 PCA-SVM machine learning to distinguish faults and lightning disturbance

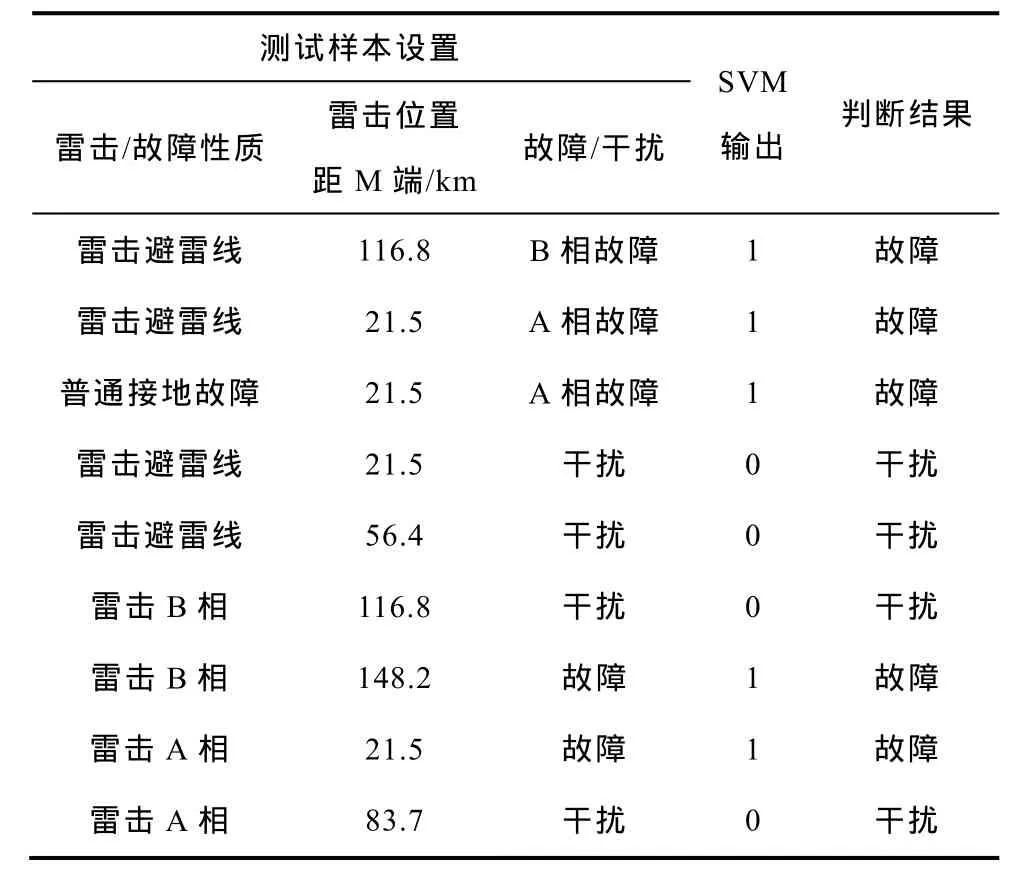
表 测试样本设置和SVM输出结果Tab. Setting of test sample and test results of SVM

7 结论

本文根据CVT与CT的实测宽频传输特性，以矢量拟合法对实际测量结果进行有理逼近，将测量得到的频域响应表示为一阶有理分式之和的形式，通过网络综合方法，利用矢量拟合得到的频域响应表达式建立对应的互感器等效电路模型。构成了基于二次侧输出的雷击干扰与故障识别元件，得到如下结论：

（1）在数值计算过程中，数值计算引起的数值振荡不可避免，利用数值计算方法得到的CVT二次侧输出包含两部分振荡，即数值振荡金额CVT传递函数极点所带来的振荡。

（2）与故障情况相比，雷击干扰不包含故障激励源引起的行波相应，利用瞬时功率能够有效的体现出故障与雷击干扰的区别，且无需考虑选相算法的配合。

（3）利用瞬时功率Δp进行PCA-SVM分类，可以对故障与雷击干扰进行区分，仿真表明，分类结果良好。

附录 CVT和CT特性与拟合结果

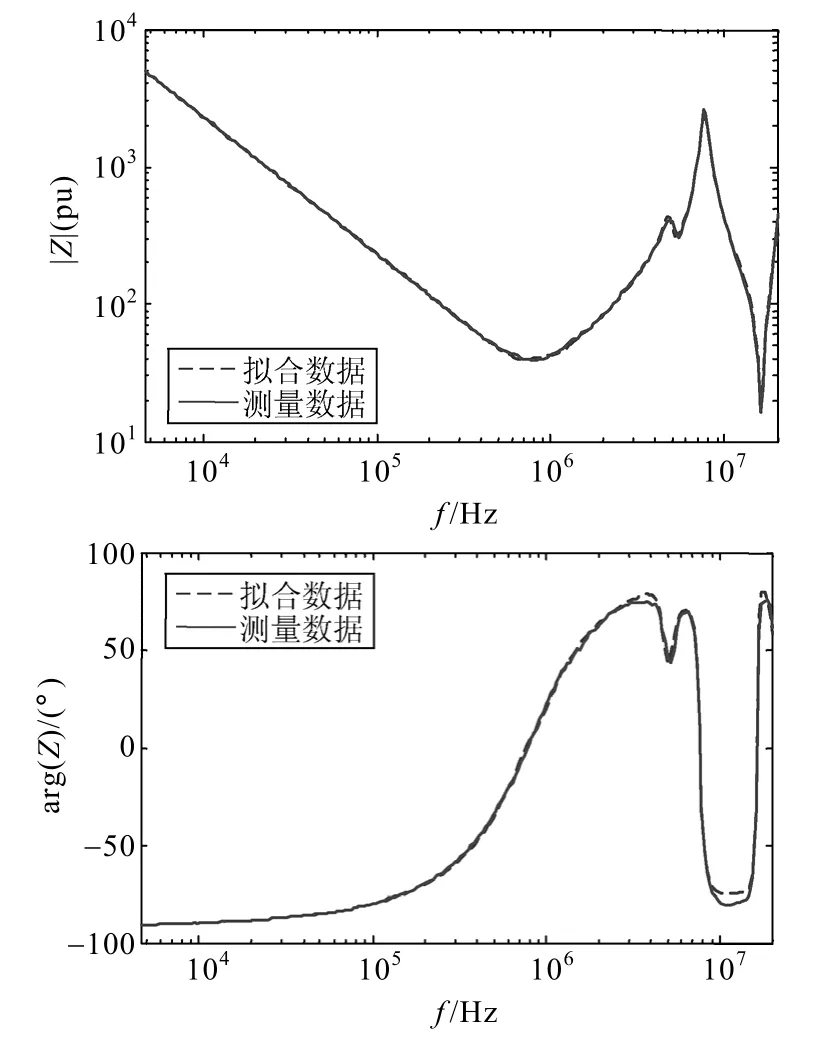
附图1 500kV电容式电压互感器T形等效电路中的Z1的拟合结果App.Fig.1 Fitting results ofZ1in the T-type equivalent circuit of 500kV CVT

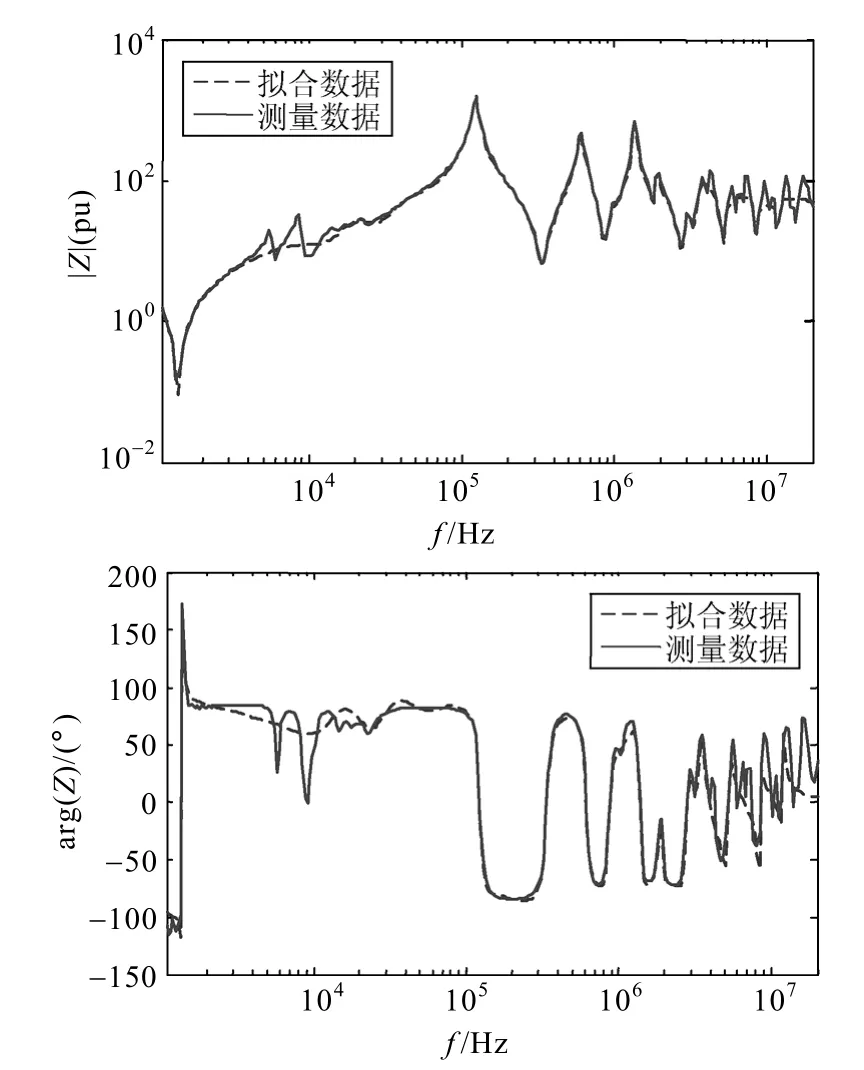
附图2 500kV电容式电压互感器T形等效电路中的Z2的拟合结果App.Fig.2 Fitting results ofZ2in the T-type equivalent circuit of 500kV CVT

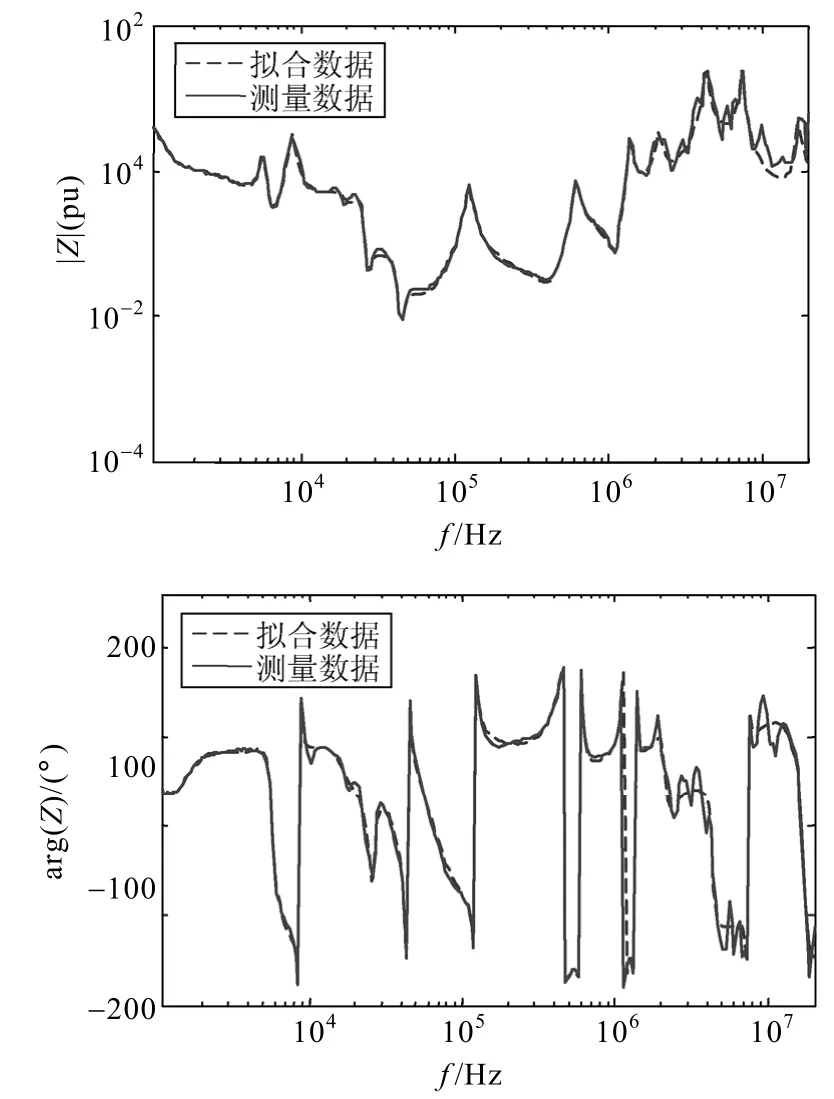
附图3 500kV电容式电压互感器T形等效电路中的Z0的拟合结果App.Fig.3 Fitting results ofZ0in the T-type equivalent circuit of 500kV CVT

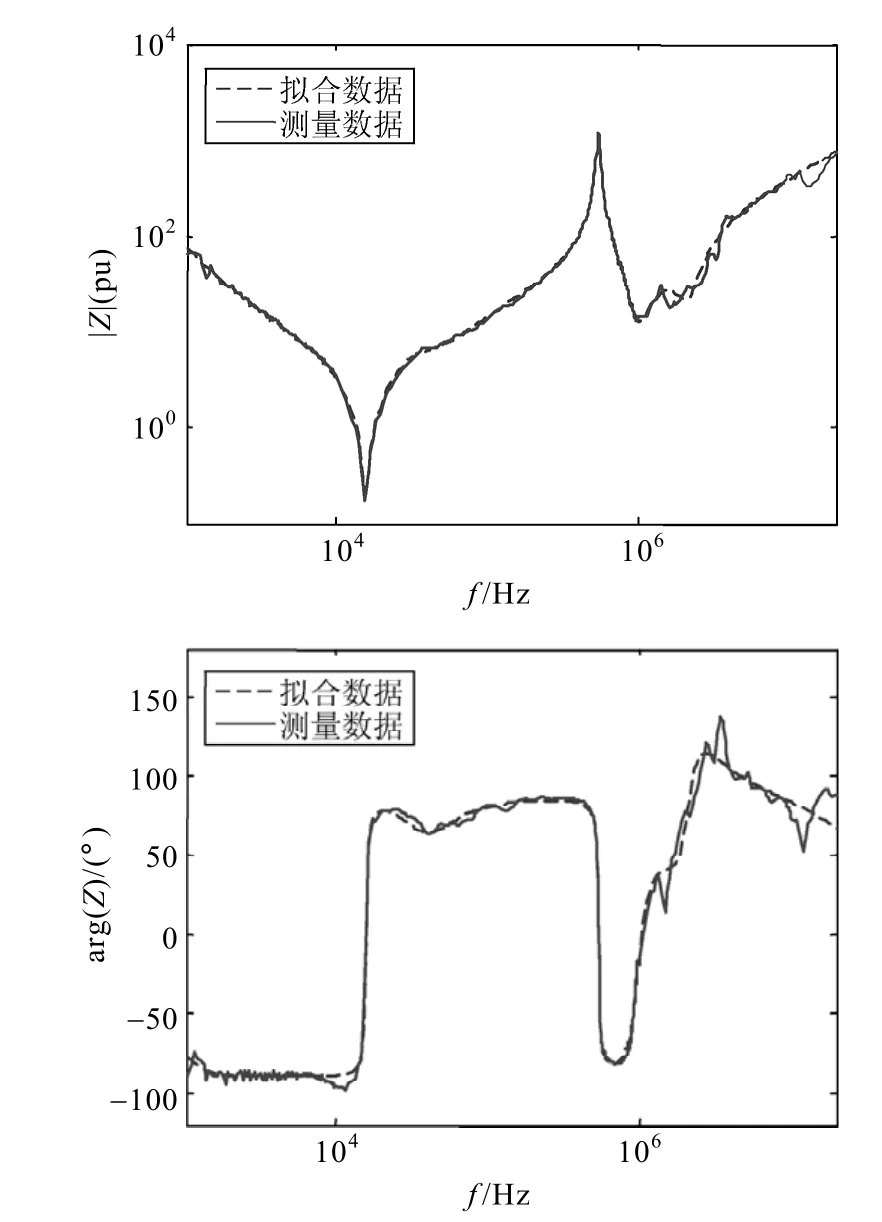
附图4 500kV电流互感器T形等效电路中的Z1的拟合结果App.Fig.4 Fitting results ofZ1in the T-type equivalent circuit of 500kV CT

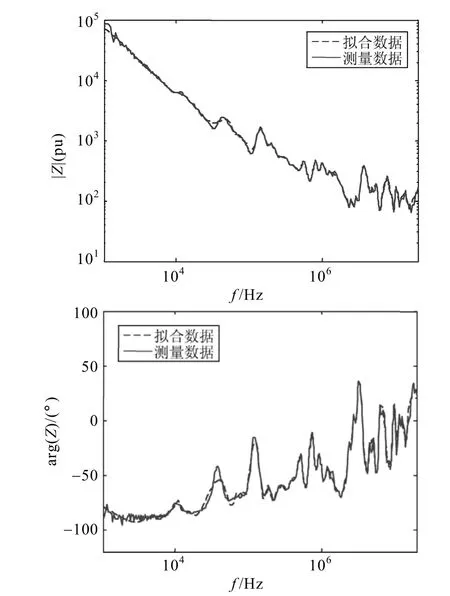
附图5 500kV电流互感器T形等效电路中的Z2的拟合结果App.Fig.5 Fitting results ofZ2in the T-type equivalent circuit of 500kV CT

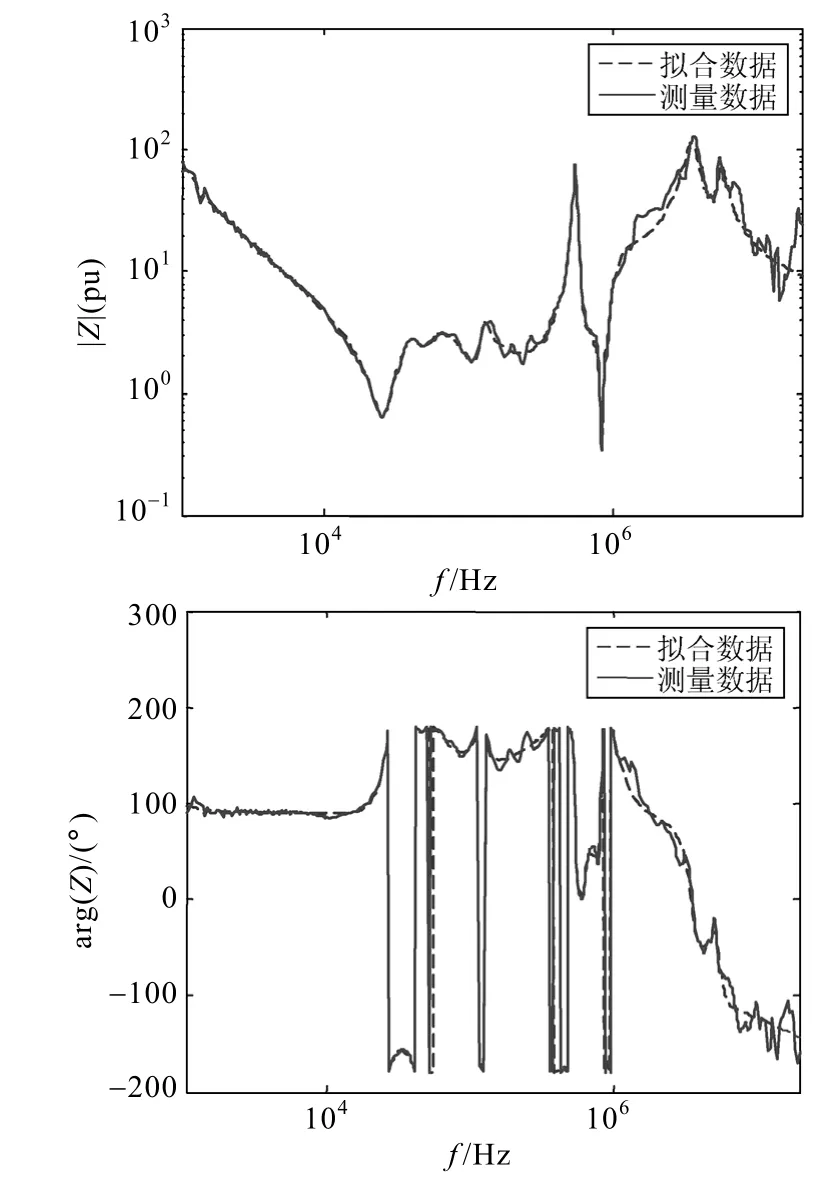
附图6 500kV电流互感器T形等效电路中的Z0的拟合结果App.Fig.6 Fitting results ofZ0in the T-type equivalent circuit of 500kV CT

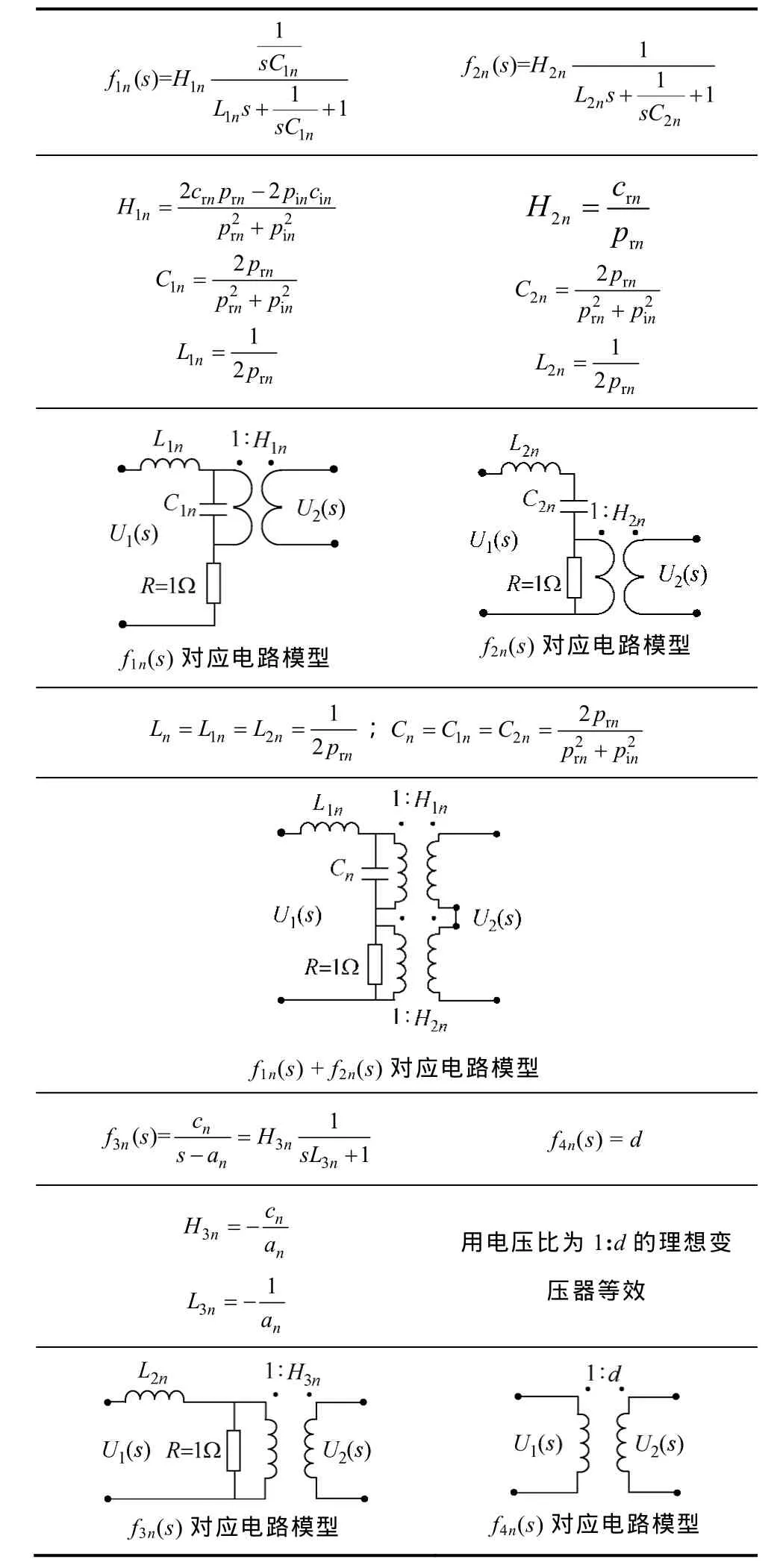
附表 基于传递函数极点和常数项的电路模型App. Tab. Circuit model based on transfer function pole and constant

[1] 司大军. 输电线路行波保护新方法研究[D]. 哈尔滨:哈尔滨工业大学,2004.

[2] 张保会,哈恒旭,吕志来. 利用单端暂态量实现超高压输电线路全线速动保护新原理研究(一)——故障暂态过程分析及实现单端暂态量保护的可行性[J]. 电力自动化设备,2001,21(6): 1-5.

Zhang Baohui,Ha Hengxu,Lü Zhilai. Study of non-unit transient-based whole-line high speed protection for EHV transmission line part 1: fault transient analysis and the feasibility of non-unit transient protection[J]. Electric Power Automation Equipment,2001,21(6): 1-5.

[3] Dommel H W,Michels J M. High speed relaying using travelling wave transient analysis[C]. IEEE PES Winter Meeting. NewYork: 1978.

[4] Bo Z Q. A new non-communication protection technique for transmission lines[J]. IEEE Transactions on Power Delivery,1998,13(4): 1073-1078.

[5] 任立,董新洲,施慎行,等. 极化电流行波方向继电器在带并联电抗器输电线上的特性[J]. 电力系统自动化,2013,37(21): 169-175.

Ren Li,Dong Xinzhou,Shi Shenxing,et al. Characteristics of polarized current travelling wave-based directional relay in transmission lines with shunt reactors[J].Automation of Electric Power Systems,2013,37(21):169-175.

[6] Bollen M H J. Traveling-wave-based protection of double-circuit lines[J]. IEE Proceedings C Generation,Transmission and Distribution,1993,140(1): 37-47.

[7] Lee H,Mousa A M. GPS Travelling wave fault locator systems: investigation into the anomalous measurements related to lightning strikes[J]. IEEE Transactions on Power Delivery,1996,11(3): 1214-1223.

[8] 段建东,任晋峰,张保会,等. 超高速保护中雷电干扰识别的暂态法研究[J]. 中国电机工程学报,2006,26(23): 7-13.

Duan Jiandong,Ren Jinfeng,Zhang Baohui,et al.Study of transient approach of discriminating lightning disturbance in ultra-high-speed protection[J]. Proceedings of the CSEE,2006,26(23): 7-13.

[9] 董杏丽,葛耀中,董新洲. 行波保护中雷电干扰问题的对策[J]. 中国电机工程学报,2002,22(9): 74-78.

Dong Xingli,Ge Yaozhong,Dong Xinzhou. Effect of lightning on protection based on travelling waves[J].Proceedings of the CSEE,2002,22(9): 74-78.

[10] 王明军. 电网雷击扰动识别方法及其应用[D]. 济南:山东大学,2012.

[11] 王刚,李海锋,赵建仓,等. 基于小波多尺度分析的输电线路直击雷暂态识别[J]. 中国电机工程学报,2004,24(4): 139-144.

Wang Gang,Li Haifeng,Zhao Jiancang,et al.Identification of transients on transmission lines caused by direct lightning strokes based on multiresolution signal decomposition[J]. Proceedings of the CSEE,2004,24(4): 139-144.

[12] 邹贵彬,高厚磊,朱峰,等. 输电线路雷击与故障的积分识别方法[J]. 电力系统保护与控制,2012,40(9): 43-48.

Zou Guibin,Gao Houlei,Zhu Feng,et al. Integral identification method of lightning stroke and fault for transmission line[J]. Power System Protection and Control,2012,40(9): 43-48.

[13] 司大军,束洪春,陈学允,等. 输电线路雷击的电磁暂态特征分析[J]. 中国电机工程学报,2005,25(7): 64-69.

Si Dajun,Shu Hongchun,Chen Xueyun,et al. Study on characteristics and identification of transients on transmission lines caused by lightning stroke[J].Proceedings of the CSEE,2005,25(7): 64-69.

[14] 束洪春,张斌,张广斌,等. 基于可拓融合的±800kV 直流输电线路雷击干扰识别方法[J]. 中国电机工程学报,2011,31(7): 102-111.

Shu Hongchun,Zhang Bin,Zhang Guangbin,et al.Identification of lightning disturbance in uhvdc transmission lines using extension theory[J]. Proceedings of the CSEE,2011,31(7): 102-111.

[15] 贺家李,宋从矩. 电力系统继电保护原理[M]. 北京:中国电力出版社,2004.

[16] 段建东,张保会,李鹏,等. 超高压输电线路新单端暂态量保护[J]. 中国电机工程学报,2007,27(7):45-51.

Duan Jiandong,Zhang Baohui,Li Peng,et al.Principle and algorithm of non-unit transient-based protection for ehv transmission lines[J]. Proceedings of the CSEE,2007,27(7): 45-51.

[17] 宋国兵,李森,康小宁,等. 一种新相模变换矩阵[J]. 电力系统自动化,2007,31(14): 57-60.

Song Guobing,Li Sen,Kang Xiaoning,et al. A novel phase-mode transformation matrix[J]. Automation of Electric Power Systems,2007,31(14): 57-60.

[18] 唐金锐,尹项根,张哲,等. 零模检测波速度的迭代提取及其在配电网单相接地故障定位中的应用[J]. 电工技术学报,2013,28(4): 202-211.

Tang Jinrui,Yin Xianggen,Zhan Zhe,et al. Iterative extraction of detected zero-mode wave velocity and its application in single phase-to-ground fault location in distribution networks[J]. Transactions of China Electrotechnical Society,2013,28(4): 202-211.

[19] Pearson K. On Lines and Planes of closest fit to systems of points in space[J]. Philosophical Magazine,1901,2(11): 559-572.

[20] Jolliffe I T. Principal component analysis,2nd Edition[M]. New York,USA: Springer,2002: 1-9.

[21] 陈妮亚,钱政,孟晓风,等. 基于空间相关法的风电场风速多步预测模型[J]. 电工技术学报,2013,28(5): 15-21.

Chen Niya,Qian Zheng,Meng Xiaofei,et al. Multistep ahead wind speed forecasting model based on spatial correlation and support vector machine[J].Transactions of China Electrotechnical Society,2013,28(5): 15-21.

[22] 史丽萍,王攀攀,胡泳军,等. 基于骨干微粒群算法和支持向量机的电机转子断条故障诊断[J]. 电工技术学报,2014,29(1): 147-155.

Shi Liping,Wang Panpan,Hu Yongjun,et al. Broken rotor bar fault diagnosis of induction motors based on bare-bone particle swarm optimization and support vector machine[J]. Transactions of China Electrotechnical Society,2014,29(1): 147-155.

[23] Vermeulen H J,Dann L R,van Roojen J. Equivalent circuit modeling of a capacitive voltage transformer for power system harmonic frequencies[J]. IEEE Transactions on Power Delivery,1995,10(4): 1743-1749.

[24] 王志华,尹项根,张小波,等. 利用 CVT捕捉电压行波实现故障测距的分析与实践[J]. 电力系统自动化,2004,28(22): 63-68.

Wang Zhihua,Yin Xianggen,Zhang Xiaobo. Analysis and practice of fault location by voltage traveling wave of CVT[J]. Automation of Electric Power Systems,2004,28(22): 63-68.

[25] 吴茂林. 变电站互感器宽频传输特性与接地网瞬态特性的研究[D]. 保定: 华北电力大学,2003.

[26] 吴宁. 电网络分析与综合[M]. 北京: 科学出版社,2003.

[27] 王斌,彭宗仁. 500kV线路绝缘子电压分布的有限元法计算[J]. 电瓷避雷器,2003(1): 13-15.

Wang Bin,Peng Zongren. A finite element method for the calculation of the voltage distribution along the 500kv line insulators[J]. Insulators and Surge Arresters,2003(1): 13-15.

[28] 束洪春,司大军,于继来. 雷击输电线路电磁暂态仿真[J]. 电力系统自动化,2005,29(17): 68-71,92.

Shu Hongchun,Si Dajun,Yu Jilai. New electromagnetic transient simulation approach considering impulsive corona and frequency-dependence line parameters[J]. Automation of Electric Power Systems,2005,29(17): 68-71,92.