制导弹药末段目标截获概率研究

刘骁，唐胜景，朱大林，郭杰

（北京理工大学飞行器动力学与控制教育部重点实验室，北京100081）

制导弹药末段目标截获概率研究

刘骁，唐胜景，朱大林，郭杰

（北京理工大学飞行器动力学与控制教育部重点实验室，北京100081）

针对末制导弹药对地面目标攻击时是否加入中制导环节，研究其末段飞行过程中与目标的几何位置关系，采用快速计算与解析方法分析其打击地面固定目标时导引头对目标的角度截获。通过空中散布椭球和地面散布椭圆的近似计算得到视场角计算公式，进而建立一般的数学模型，并从统计概率角度，得到末制导目标截获概率，根据3σ原则判断是否加入中制导环节。同时研究了零控脱靶量与末制导修正距离，结果表明末制导修正能力满足零控脱靶量。仿真发现导引头开机位置距离目标逐渐变小时，视场角的置信区间先减小、后增大。计算了不同干扰因素对视场角置信区间的影响，结果表明水平风对视场角分布的影响比侧风的影响要大。

兵器科学与技术；末制导；目标探测；蒙特卡洛法；截获概率

0　引言

远射程始终是战术武器设计追求的一个目标，本文研究有助推发动机的末制导迫击炮炮弹便是增程武器的一种。但随着制导弹药射程的增加需要考虑是否加入中制导环节，另一方面制导弹药进入末制导首先要得知目标方位信息，这可以在末制导前由导引头探测获得。由于误差的存在，进入末制导后导引头开机时不一定能发现目标。这需要在设计中加入中制导环节，以赋予其末制导时具有较好地初始位置与角度，以便导引头能够顺利地发现与捕获目标。但是中制导的加入使得制导弹药成本增加，所以准确的判断是否需要中制导环节，成为了关键问题。

导引头截获目标包含目标的距离截获、角度截获和速度截获。导引头截获目标概率由（1）式计算［1］：

式中：Pm为导引头雷达截获概率；PD为距离截获概率，制导设备正常下通常认为PD≈1；Pv为速度截获概率，它需要考虑目标多普勒频率落入导引头滤波器组频率宽内的频率和目标回波的截获概率，本文主要考虑Pα，即角度截获概率。文献［2］针对末段修正迫击炮炮弹建立了激光探测器模型和目标方位模型。文献［3］研究了脉冲启控时刻、脉冲个数和修正模式对末段修正迫击炮炮弹修正效果的影响。文献［4］针对远程打击武器，用蒙特卡罗法计算了末制导截获概率。文献［5］分析了导弹角度截获概率和距离截获概率的数学模型，并介绍了目标截获概率的仿真计算方法。文献［6］分析了导弹的中末制导和交接前后目标状态的估计误差，以及截获概率与交接班时弹目几何位置关系。文献［7］介绍了影响协同制导的主要误差及误差特性，建立了中末制导交接班目标截获概率计算模型，得到了截获概率与误差的定量关系。文献［8］与文献［9］分析了自寻地导弹末制导获得目标信息的要求并进行了弹道优化。文献［10］对导弹制导系统开始导引的启控点进行了研究。这些文献的共同特点是：

1）基本只考虑了弹道落点的散布情况，即地面散布椭圆，而没有考虑在飞行中导引头开机时，由于误差的存在也是有散布的，即空中散布椭球。

2）提及空中散布的文献，没有从一般情况，分析椭球半轴的边界点与地面落点对应情况。

本文针对末制导迫击炮炮弹类型的制导弹药打击地面固定目标，建立数学模型并对制导弹药与目标的几何位置关系进行研究。既考虑到导引头开机点空中散布情况，也考虑到地面落点的散布椭圆，分析了二者边界点对视场角的计算影响，从统计概率角度得出一般结论，为判断是否加入中制导环节提供了参考依据。

1　数学建模

假设末制导迫击炮炮弹发射后，首先经过助推快速爬升，飞过最高点后由弹载设备判断弹目距离，小于导引头探测距离后，导引头开机进入末制导，直至摧毁目标。因为有助推阶段，整个飞行距离较长，加之导引头作用距离有限，需要考虑中制导是否加入的问题。但如果末制导导引头开机时能够迅速捕获目标，则可以不加中制导。接下来对上述问题建模，并计算导引头视场角。

1.1导引头视场角快速计算

如图1所示坐标系为地面坐标系，迫击炮炮弹发射点为原点。发射后经过助推阶段，飞过最高点后导引头开机工作，之后进入末制导直至目标被摧毁。假设导引头光轴与迫击炮炮弹弹轴重合，导引头视场角为±Θ探测区域形成圆锥面，导引头光轴与地面相交于C点。

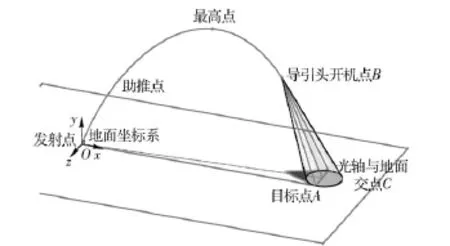
图1　导引头视场角几何示意图Fig.1 Geometric graph of FOV angle of seeker

如果圆锥面能够覆盖目标点A，则表示导引头能够探测到目标方位，从而进入末段导引。进一步，若图1中△ABC中∠ABC，即圆锥半顶角能够小于导引头视场角给定值，也可以证明导引头能够看见目标点。如果目标点A在圆锥面覆盖范围之外，则导引头不能发现目标。此时需要加入中制导环节。

在弹道仿真中，可以得到以射程中间误差和方向中间误差为半轴的等概率密度椭圆［11］。在n次仿真实验后，导引头开机位置点B在空间中是n个散布点，一般情况下这n个散布点可以近似为一个椭球。空间散布点对应地面上的散布点，同理这地面上n个散布点可以近似为一个椭圆。如图2所示。

图2　目标视线角示意图Fig.2 Schematic diagram of target line of sight

图2中椭球和椭圆可以表示为

式中：x0、y0、z0分别是n个离散点在地面坐标系下，对应3个轴的均值，即椭球的中心点；xC和yC分别是地面散布点在x和y轴方向的均值，即C点的横、纵坐标；a、b、c与a1、b1分别是椭球和椭圆的半轴。如图1所示，椭球上坐标点B与落地点椭圆上的点A和椭圆中心点，这三点形成三角形。假设椭圆中心为导引头光轴与地面交点。椭球上一点为导引头开机位置，假设目标点在地面椭圆范围内。则△AiBjC（i=1，2，3，4；j=1，2，3，4，5，6）中∠AiBjC即为视场角。由于AB各有4、6个点，所以∠AiBjC有24个值，可以组成一个矩阵。根据余弦定理，

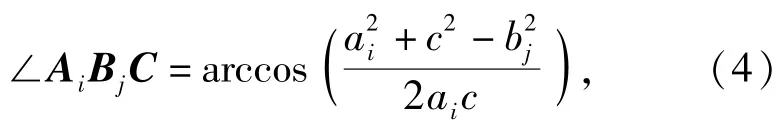
式中：ai、bj、c分别为三角形三边长度。通过弹道仿真，可以计算3个顶点的坐标，进而可以求出其大小，最后与弹轴偏离视线的平均角度相加得到视场角大小。从（4）式可以看出，a、c取最大，同时bj取最小时∠AiBjC达到最大值。进一步分析A、B取最远端时a到达最大，b为椭圆短半轴时最小。假设x轴方向飞行距离远大于另外两轴的飞行距离，那么x轴方向的均方差σx较大，a=3σx也较大，所以起主要作用。故∠AiBjC最大值应为沿x方向的长半轴最大值，即椭球与椭圆端点形成的视场角。

这种方法没有考虑目标点具体位置，只假定其在地面散布椭圆内部，而直接计算最坏的情况，即椭球椭圆端点形成的视场角大小，如果这种情况下能够小于给定的视场角，则说明一定可以探测到目标，计算效率高，故称快速计算。

1.2导引头视场角解析法与统计特性

导引头视场角的解析法如下：通过多次的飞行仿真模拟，得到A、B、C点的位置。其中A点坐标通过无控理想弹道仿真得到，这里认为无控理想弹道的落点为目标点。B点是由打靶仿真得到。C点的求解假设导引头无安装角，光轴视线与弹轴视线重合。B点沿弹轴方向形成一条斜线，它与地面的交点即为C点。按照空间直线表示方法，

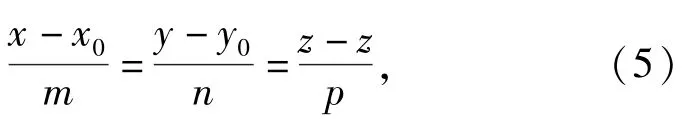
式中：m、n、p为这条直线的方向数，（m，n，p）这组向量的方向余弦是直线的方向余弦。同时按照坐标变换，表征姿态的俯仰角ϑ、偏航角ψ与方向数有如下关系：

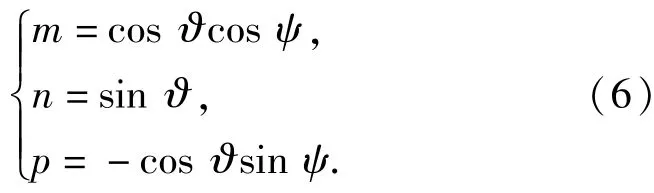
已知导引头开机点坐标（x0，y0，z0）即B点，再令（5）式中y=0，可以求出空间直线与地面的交点C.计算出一组三坐标（A、B、C），可以由余弦定理解出这组视场角∠ABC的大小，以上内容就是导引头视场角解析法。进一步计算所有仿真中视场角的大小，得到其均值与标准差和置信区间。将计算得到的置信区间与已知的导引头视场角进行比较，可以判断末制导导引头开机时能否探测到目标。为了保证导引头能够有效探测到目标，采用3σ原则，即概率大于99.7%才认为探测成功。

现在考虑这样一个问题，假设导引头无安装角，光轴与弹轴方向相同，那么导引头开机位置也十分重要，由于迫击炮炮弹在不同开机位置会有不同姿态，而姿态直接影响导引头光轴方向，过早或过晚的开机可能出现目标不在视场范围内，进而无法探测到目标。如图3所示，过早的开机例如B1点开机，虽然视场探测范围大，但探测方向不指向目标区域，所以探测不到目标点A.而导引头过晚的开机会使视场范围过小，同样无法探测到目标。所以选定导引头合适的开机位置才能使目标落在导引头视场区域内。

图3　导引头开机位置示意图Fig.3 Starting-up location of seeker

具体开机位置可以通过弹道仿真确定其范围。

2　仿真结果与分析

2.1扰动因素分布范围

针对圆锥半顶角的情况，本文采用蒙特卡洛模拟打靶，从概率角度分析视场角覆盖问题。假设导引头视场角Θ=±8°，考虑的扰动因素及其分布类型如表1所示。

表1　扰动因素及其分布范围Tab.1 Disturbance factors and their distribution

2.2导引头视场角散布仿真结果

弹道仿真初始条件：初速v0=278 m/s，射角θ0=45°，500次模拟获得的导引头开机点散布结果如图4所示。

此时根据导引头开机点的分布，首先计算x0、y0、z0，它们分别是离散点在地面坐标系下对应3个轴的均值，即椭球的中心点；接下来得到在地面坐标系下椭球中a、b、c 3个半轴的长度，进而得出迫击炮炮弹飞行中，导引头开机点形成的概率椭球。如图5所示。

如图5所示的概率椭球，内部包括边界点即是导引头控制开机位置，图中基本覆盖所有空中散布点，计算结果满足3σ原则，即导引头开机点落在椭球范围内的概率大于99.7%。接下来计算导引头开机点在地面坐标系下的中间偏差。中间偏差的大小反映了散布点距离均值中线点的偏离程度。表2为导引头开机点散布统计结果。

图4　导引头开机点散布Fig.4 The distribution of the seeker starting-up points

图5　导引头开机点散布椭球Fig.5 Distributed ellipsoid of the seeker starting-up points

表2　导引头开机点散布统计结果Tab.2 The distribution of the statistical results of theseeker starting-up points

表2中Ex、Ey、Ez为导引头启动点在地面坐标系下的中间偏差。其中Ex=0.674 5σx，Ey、Ez也与对应的均方差有类似关系。这500个空间散布点对应地面500个散布点，地面上的散布点可以近似为一个椭圆。椭圆的长半轴是这些点在x方向的均方差的3倍（3σ原则），同理可以求出椭圆的短半轴。如图6所示。

从图6可以看出，仅有极少点在椭圆范围外，但满足3σ原则，即仿真结果中落在椭圆范围内的概率大于99.7%，故该概率椭圆可以反映迫击炮炮弹落点分布。

2.3零控脱靶量

仿真初速v0=278 m/s，射角θ0=45°，由上述弹道仿真可得结果：交班时刻：水平方向（x方向）零控脱靶量均值为78 m，侧向（z方向）零控脱靶量均值为28 m.两方向均方差分别为99 m与35 m.

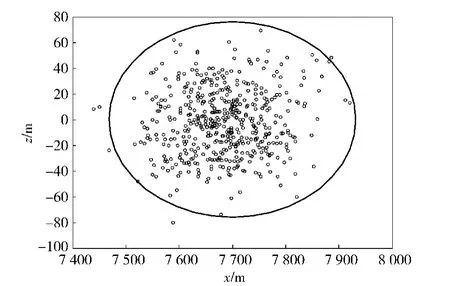
图6　地面落点散布椭圆Fig.6 The distribution of impact points in ellipse

分析迫击炮炮弹从距离目标1.0 km、2.5 km处舵面开始动作的修正能力，舵偏角取为5°，获得的仿真结果如表3所示。

表3　控制能力仿真结果Tab.3 The simulation results of maneuvering ability

由表3可以看出，迫击炮炮弹的修正能力可以满足交接班时刻的零控脱靶量。这意味着如果导引头能够捕捉到目标，那么制导迫击炮炮弹可以通过控制修正，进而准确打击目标。

接下来首先按照快速求解的方法，判断是否一定要加入中制导。结果如表4所示。

表4　视场角∠AiBjC矩阵Tab.4 FOV angle∠AiBjC matrix

考虑视场角矩阵的最大值4.74°与弹轴偏离视线的平均角度为7.2°相加（这里为500次仿真的均值），则所需视场角为11.94°大于导引头视场角Θ= ±8°。但由于部分值与弹轴偏离视线的平均角度之和小于导引头视场角Θ=±8°，所以还不能判断一定需要加入中制导环节。

2.4视场角解析结果与散布概率统计

接下来考虑一般情况的仿真分析。计算∠ABC首先获得点B坐标和当前俯仰角，其次求出迫击炮炮弹沿光轴方向与地面交点C，目标点A由无控仿真理想落点确定。得知三点坐标后，可以由余弦定理解出∠ABC大小。按照前面的分析，选定6个导引头开机位置，分别选取距离目标2 250 m、1 750 m、1 500 m、1 250 m、1 000 m、750 m位置开机。经500次弹道仿真，视场角计算结果如图7和图8所示。

图7　视场角分布（距离目标2 250 m）Fig.7 The distribution of FOV angles（The distance from the target is 2 250 m）

图8 视场角分布（距离目标1 500 m）Fig.8 The distribution of FOV angles（The distance from the target is 1 500 m）

图7仿真初值为278 m/s，45°发射角。进一步求出视场角分布的均值为8.1°，均方差为1.1°.3σ置信区间即为（4.8°，11.4°），视场角最小为5.06°，最大为11.24°.仿真实验的置信区间最大值在8°以外，说明导引头开机时不能以大于99.7%的概率看到目标点。由图8得出仿真实验的置信区间范围在8°以内，说明导引头开机时能够看到目标点的概率大于99.7%.

图9初始条件不变，得出置信区间最大值为10.9°，大于8°，这说明导引头开机时的探测概率不满足要求。对交班时刻零控脱靶量与视场角散布结果分析得到相应统计值，汇总到表5、表6.

图9　视场角分布（距离目标750 m）Fig.9 The distribution of FOV angles（The distance from the target is 750 m）

表5　不同开机位置零控脱靶量统计结果Tab.5 Zero-effort miss results in different boot positions

由表3、表5可以看出迫击炮炮弹的修正能力可以满足导引头不同开机位置的交接班时刻的零控脱靶量。

因为圆锥半顶角几何上没有负值，所以表6置信区间最小为0°.如表6所示，导引头在距离目标2 250 m开机时，3σ置信区间为（4.8°，11.4°），这说明目标点没有全部落在视场范围内，即置信区间最大值超过导引头视场角能提供的最大值8°.而随着导引头开机距离的靠近，在1 250 m的3σ置信区间为（0°，6.2°），说明目标点全部落在导引头范围内的概率大于99.7%，即认为完全看见目标点；而导引头在750 m开机时，3σ置信区间为（0°，10.9°），置信区间又不在8°以内，说明又出现目标点没有全部落在视场范围内。造成这种视场角先减小、后增大的原因是因为：若导引头开机过早，则不能对准目标区域，无法探测到目标。此时导引头的指向方向与目标点的方向夹角，也就是视场角较大；而导引头开机过晚虽然指向目标方向，但视线距离过短，故不能覆盖目标点。所以通过置信区间可以判断目标截获概率，同时导引头开机范围也可以从表6中获得。

要说明的是：本文采用3σ原则，探测概率要求要超过99.7%，故指标较为严格，实际工程应用可以提出对应的探测概率的指标，相应计算方法仍可参考本文。

表6　不同开机位置视场角散布统计结果Tab.6 View angle distribution results in different boot positions

2.5单一扰动因素对视场角的影响

接下来讨论单一因素对目标截获概率的影响。针对上文提出的9种干扰因素，单一施加于弹道仿真过程中。得到每种仿真对视场角大小的分布。计算每种干扰下的视场角均值与均方差大小，得到视场角的置信区间。仿真初始条件为：初速v0=278 m/s，射角θ0=45°，导引头开机位置为距离目标2 000 m，扰动大小如表7所示，扰动因素分布均为正态分布。结果如表7所示。

由表7可以看出：水平风对视场角分布的影响比侧风的影响要大；弹道倾角、弹道偏角和初始速度偏差对视场角置信区间影响不大，小于0.1°；初始角速度ωy0与ωz0对视场角分布影响可以忽略；点火时间对视场角散布影响较大，仅次于水平风的影响；推力偏差对视场角置信区间大小影响体现在均方差为0.3°.

3　结论

本文针对制导迫击炮炮弹是否加入中制导环节，首先建立末制导过程中目标与迫击炮炮弹的几何关系模型，通过概率椭球与概率椭圆的近似计算，得到导引头视场角的公式，即快速判断是否一定要加入中制导环节的计算公式。其次建立更一般的导引头视场角计算理论即解析方法，进而可以利用置信区间判断末制导截获目标概率。采用这样的理论方法可以有效判断是否采用中制导。仿真中利用蒙特卡洛模拟打靶分析，给定初始条件，经过打靶仿真得到统计结果，根据3σ置信区间得到多种开机位置的目标探测概率。发现随着导引头开机位置距离目标逐渐变小时，视场角的置信区间先减小、后增大，这说明导引头开机位置要合适，过早或过晚的开机都无法发现目标。计算了交接班时刻的零控脱靶量和迫击炮炮弹的控制修正能力。计算表明，通过控制系统的修正能够覆盖脱靶量，进而准确地打击目标。最后针对多种干扰因素，分析不同干扰对视场角置信区间大小的影响。分析研究得到结论：水平风对视场角分布的影响比侧风的影响要大，并且对视场角置信区间的影响也十分明显，需要重点考虑。

表7　不同干扰因素对视场角散布的影响Tab.7 The effects of different disturbance factors on FOV angle distribution

（

）

［1］蓝伟华.火控系统误差与雷达型空空导弹截获目标概率计算［J］.电光与控制，2004，11（3）：14-17. LAN Wei-hua.Error of FCS and calculation of interception probability for radar guided air-to-air missiles［J］.Electronics Optics& Control，2004，11（3）：14-17.（in Chinese）

［2］徐劲祥.末段修正迫弹激光探测器及目标方位模型［J］.兵工学报，2007，28（7）：793-795. XU Jin-xiang.Models of laser detector and target azimuth for terminal correction mortar projectile［J］.Acta Armamentarii，2007，28（7）：793-795.（in Chinese）

［3］曹营军，高敏.末修迫弹修正效果影响因素分析［J］.军械工程学院学报，2009，21（1）：24-27. CAO Ying-jun，GAO Min.Analysis of correction effect of terminal trajectory correction on mortar projectile［J］.Journal of Ordnance Engineering College，2009，21（1）：24-27.（in Chinese）

［4］秦荣华.远程攻击末制导目标截获概率数字仿真［J］.上海航天，2005，22（3）：26-28. QIN Rong-hua.Simulation of target air capture probability of aerocraft terminal guidance for long-distance attack［J］.Aerospace Shanghai，2005，22（3）：26-28.（in Chinese）

［5］付海峰，刘华伟，张宗麟，等.中距主动制导空空导弹目标截获概率仿真计算［J］.电光与控制，2007，14（3）：55-58. FU Hai-feng，LIU Hua-wei，ZHANG Zong-lin，et al.Simulated computation of target-acquisition probability of medium-range active-guided AAM［J］.Electronics Optics&Control，2007，14（3）：55-58.（in Chinese）

［6］屈剑明，毛士艺，李少洪.雷达导引头交班与弹目几何位置关系研究［J］.北京航空航天大学学报，2000，26（3）：274-277. QU Jian-ming，MAO Shi-yi，LI Shao-hong.Research on the relation between the seeker's handover and the geometrical position of the missile and the target［J］.Journal of Beijing University of Aeronautics and Astronautics，2000，26（3）：274-277.（in Chinese）

［7］付昭旺，于雷，寇英信，等.导弹协同制导中末交接班目标截获概率研究［J］.弹道学报，2012，24（4）：31-36. FU Zhao-wang，YU Lei，KOU Ying-xin，et al.Target acquisition probability in midcourse and terminal guidance handing-off for cooperative guidance of missile［J］.Journal of Ballistics，2012，24（4）：31-36.（in Chinese）

［8］Asthana C B，Prahlada.Evaluation of missile seeker dwell time for three-dimensional aerial engagements［J］.Journal of Guidance，Control and Dynamics，1994，17（1）：211-214.

［9］Farooq A，Limebeer D J N.Trajectory optimization for air-to-surface missiles with imaging radars［J］.Journal of Guidance，Control and Dynamics，2002，25（5）：876-887.

［10］朱大林，唐胜景，郭杰，等.稳健优化在导弹启控点选择中的应用［J］.弹道学报，2013，25（1）：22-26. ZHU Da-lin，TANG Sheng-jing，GUO Jie，et al.Application of robust optimization to selection of missile initial control points［J］. Journal of Ballistics，2013，25（1）：22-26.（in Chinese）

［11］杨绍卿.火箭外弹道偏差与修正理论［M］.北京：国防工业出版社，2011：1-3. YANG Shao-qing.The trajectory error and correction theory of rockets［M］.Beijing：National Defense Industry Press，2011：1-3.（in Chinese）

Research on Target Acquisition Probability in the Terminal Guidance of Guided Munition

LIU Xiao，TANG Sheng-jing，ZHU Da-lin，GUO Jie
（Key Laboratory of Dynamics and Control of Flight Vehicle of Ministry of Education，Beijing Institute of Technology，Beijing 100081，China）

The addition of the midcourse guidance in the guided munition attack and the geometrical position between the missile and the target during the missile flight are studied.The key analysis focuses on the angle of the target intercepted from the seeker when the missile attacks the ground fixed target.The fast calculation method and the analytic method are put forward.In the result of the approximate calculation which is from the space distribution ellipsoid and the ground distribution ellipse，the view angle calculation formula is derived.Furthermore，a general mathematical model to get the target acquisition probability from the view of statistical probability is created.According to the 3σ principle，whether to add the midcourse guidance is decided.The zero-effect miss and the maneuvering ability of the guided munition are researched.The results show that the maneuvering ability of the guided munition covers the zeroeffort miss.The confidence interval of the view angle first decreases and then increases when the distance between the seeker and the target decreases.Finally，the influences of different disturbance factors on the view angle's confidence interval are calculated.The calculated results show that the wind in x direction has more influence on the view angle than the wind in z direction.

ordnance science and technology；terminal guidance；target detection；Monte Carlo meth-od；intercept probability

TJ765.3

A

1000-1093（2015）02-0287-07

10.3969/j.issn.1000-1093.2015.02.014

2014-03-14

刘骁（1988—），男，博士研究生。E-mail：liuxiao88525@163.com；唐胜景（1959—），男，教授，博士生导师。E-mail：tangsj@bit.edu.cn