某大口径榴弹炮弹带挤进过程数值模拟研究

孙全兆，杨国来，王鹏，葛建立，谢润

（南京理工大学机械工程学院，江苏南京210094）

某大口径榴弹炮弹带挤进过程数值模拟研究

孙全兆，杨国来，王鹏，葛建立，谢润

（南京理工大学机械工程学院，江苏南京210094）

为探索某大口径榴弹炮发射条件下弹带挤进过程的力学机理，建立了弹带挤进坡膛的有限元模型。通过数值模拟研究弹带的动态挤进过程，分析弹带变形及刻槽形成过程，计算得到弹带动态挤进阻力、挤进压力和弹丸运动规律，给出了最大挤进阻力值、挤进压力值及对应时刻弹丸速度值。研究结果表明，挤进过程中弹带材料经历塑性变形流动，发生剪切失效占主导的韧性断裂并形成刻槽，弹带挤进后具有明显的层状特征，其内部区域的塑性变形量很小，弹带绝热变形产生的热量不足以使弹带材料熔化。文中采用的实验测试数据为数值模拟研究提供了支持，下一步工作的重点是开展针对弹带动态挤进阻力及弹丸运动规律的实验研究。

兵器科学与技术；弹带挤进；弹带变形；挤进阻力；挤进压力；有限元模拟

0　引言

火炮发射条件下的弹带挤进过程具有高瞬态、高温强冲击、高速摩擦、大变形等复杂特点，经典内弹道理论忽略挤进过程，认为挤进过程瞬时完成，直接将挤进压力作为弹丸开始运动的起动压力，而不考虑挤进时期火药气体压力和弹丸速度的变化过程。随着现代火炮向高初速、远射程、高射速和高精度方向发展，弹带挤进过程对火炮膛压、初速、射击精度、身管寿命以及安全性等性能指标产生的影响更显著，瞬时挤进假设理论难以适用，需要研究弹带的动态挤进过程。

文献［1-3］等经典理论工作中，针对弹带挤进阻力的研究受限于计算手段，对于弹带大变形弹塑性力学及材料损伤失效的计算过于简化。文献［4］从弹带挤进的角度研究了火炮内弹道峰现象的机理及其影响，其挤进压力和挤进阻力的计算仍然采用经典理论公式，有一定局限性。文献［5］采用有限元法和ABAQUS软件进行了挤进过程大变形和弹丸旋转弹带磨损分析，将身管和弹丸作为刚体，假设身管内膛是光滑对称的，铜弹带采用弹塑性模型，考虑摩擦因素，计算得到了挤进过程弹带和身管上的接触力。由于采用身管内膛光滑假设和不考虑弹带损伤失效的材料模型，计算模型与物理对象有较大差异。文献［6-7］就弹带构造对火炮身管受力的影响进行了非线性有限元数值计算和实验分析，但是略去膛线，将身管简化成光滑内膛，并只取周向一部分研究，使其分析与真实挤进过程偏差较大。文献［8］对两种大口径榴弹炮弹丸铜质弹带挤进坡膛过程进行了有限元计算，得到了变形、应力及相互作用力结果，但采用的是基于轴对称单元的二维模型分析，同样存在对物理几何过度简化的问题。文献［9］针对弹丸在枪管挤进过程中带有过盈摩擦大变形接触问题，运用动态显式算法以及网格自适应技术，通过有限元方法数值模拟研究了铅芯弹头的挤进过程，分析了弹头上压痕的形成过程和材料的流动情况，但是其所用膛压曲线数据是瞬时挤进假设下的计算值，载荷的施加存在合理性问题。文献［10-11］引入弹带材料的初始损伤及累计损伤模型，对在两种不同结构坡膛条件下的弹带挤进过程进行显式非线性有限元计算，得到了挤进过程中弹丸及弹带的动力学响应，分析了坡膛结构变化对挤进冲击力及内弹道性能的影响。但是，这些研究工作对初始内弹道中关注的动态挤进阻力和挤进压力等问题涉及较少，对弹带材料大变形及断裂失效模式的分析仍需补充完善。

为探索某大口径榴弹炮发射条件下弹带挤进过程的力学机理，本文运用有限元方法，建立其弹带挤进线膛身管坡膛的三维有限元网格模型，采用考虑弹塑性大变形及断裂失效的弹带材料模型，以实测弹底压力作为载荷数据，通过数值模拟研究挤进过程中弹带塑性变形流动，由应力三轴度和Lode角参数判断弹带的断裂失效模式，并分析刻槽形成机理，由弹带变形后的温度分布考查弹带材料是否熔融，最终计算获取弹带动态挤进阻力、挤进压力和弹丸运动规律。

1　弹带挤进过程及模型假设

1.1弹带挤进坡膛的过程

该大口径榴弹炮射击时，首先将弹丸装填到炮膛的正确位置。为了更好地密闭膛内火药气体，提供较为稳定的弹丸起动压力和良好的内弹道性能，弹丸采用带凸台的双弹带结构，且主弹带留有一定弹带强制量。装填后，弹带与坡膛紧密接触，使药室处于密闭状态。火炮发射时，膛内气体压力逐渐上升，当达到起动压力时，弹丸开始运动，弹带产生塑性变形逐渐挤进膛线。弹带的变形阻力随弹带挤进坡膛的长度而增加，直至最大值。之后随着弹带变形量减小，阻力减小。当弹带及其延伸部分全部进入身管膛线部，挤进终了。

1.2模型假设

为简化计算模型，作如下假设：

1）不考虑卡膛过程，初始时弹带凸台与药室前的坡膛密切接触而定位，不计弹带的初始应力和变形。

2）忽略身管、弹丸本体的变形，假设它们为刚体；忽略弹丸的动不平衡，将弹丸前端和尾部截去，以等效质量代替。

3）不考虑身管的后坐运动；不计弹丸前端空气动力的影响，也不计重力。

4）不计温度应力场；假设挤进过程中弹带材料变形为绝热过程；不考虑摩擦产生的热量。

2　弹带挤进过程的有限元模型

2.1有限元网格

弹带、弹丸本体、身管坡膛段的网格采用八节点六面体单元。弹带是挤进成形的关键部位，应采用细化网格。弹丸本体和身管坡膛段是刚性体，其网格尺寸可以稍大。根据模型试算的收敛性情况确定网格的基本尺寸，建立网格模型如图1所示，共有1 748 736个单元，其中弹带部分有1 156 800个单元。

图1　有限元网格模型Fig.1 Finite element mesh

所建立的有限元模型运用LS-DYNA软件［12］的拉格朗日算法显式求解，采用单点积分和基于刚性的沙漏控制，既有利于大变形计算稳定可靠［13］，又节省计算机资源。

2.2材料模型

弹带材料为H90黄铜，弹丸本体材料为弹钢，身管材料为炮钢。

弹带在挤进过程中经历弹塑性大变形及损伤，最终发生局部化韧性断裂，涉及到弹带材料的应变硬化、应变率硬化和温度软化，故采用Johnson-Cook塑性及断裂失效模型。

2.2.1Johnson-Cook塑性模型

Johnson-Cook塑性模型［14］中，von Mises屈服应力是塑性应变、应变率以及温度的函数。

式中：εp为等效塑性应变；为等效塑性应变率；为参考应变率；T为温度；Tr为室温；Tm为熔化温度；A、B、C、m和n是常量。

绝热过程引起的温度改变为

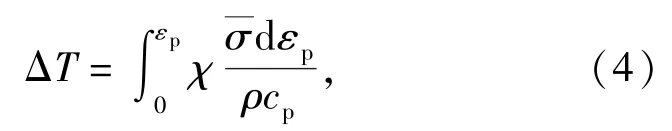
式中：ρ为材料密度；cp为比热；χ为Taylor-Quinney系数，表示塑性功转化为热的比例，一般为0.85～0.95，本文取0.9.

2.2.2Johnson-Cook断裂失效模型

Johnson-Cook断裂失效模型［15］以等效塑性失效应变来界定损伤：

式中：D1～D5为材料断裂失效参数；σ*为应力三轴度，即静水应力σm与von Mises等效应力σeq的比值，其表达式为

采用线性损伤演化规律，材料累积损伤参数为

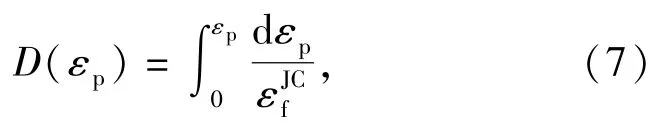
式中：当D=1时，材料断裂失效。

挤进过程数值计算中，弹带材料断裂失效通过LS-DYNA中的单元删除方法模拟。

2.2.3Gruneisen状态方程

对于动态问题，一般将金属材料变形分解为体积项和剪切项。其中，材料的剪切强度一般由不依赖于静水压力的热粘性本构关系描述，而静水压力通常由描述压力与相对体积及其他热学参量关系的状态方程来确定，本文中采用Gruneisen状态方程［16］。

材料受压缩时，Gruneisen状态方程定义材料所受压力为

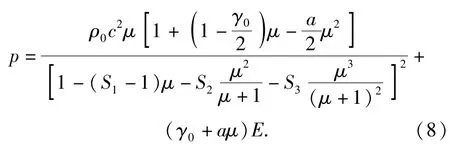
当材料膨胀时，Gruneisen状态方程可用下式表示：

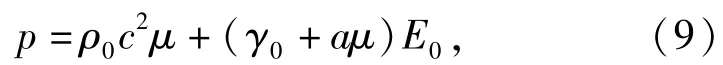
式中：c是冲击波波速与波后质点粒子速度曲线的截距，体积声速；S1、S2、S3是us-up曲线的斜率系数；γ0是Gruneisen Gamma系数；a是对γ0的1阶体积修正；E0为初始单位体积内能；ρ0为材料初始密度；

计算所用的弹带材料模型参数列于表1中。

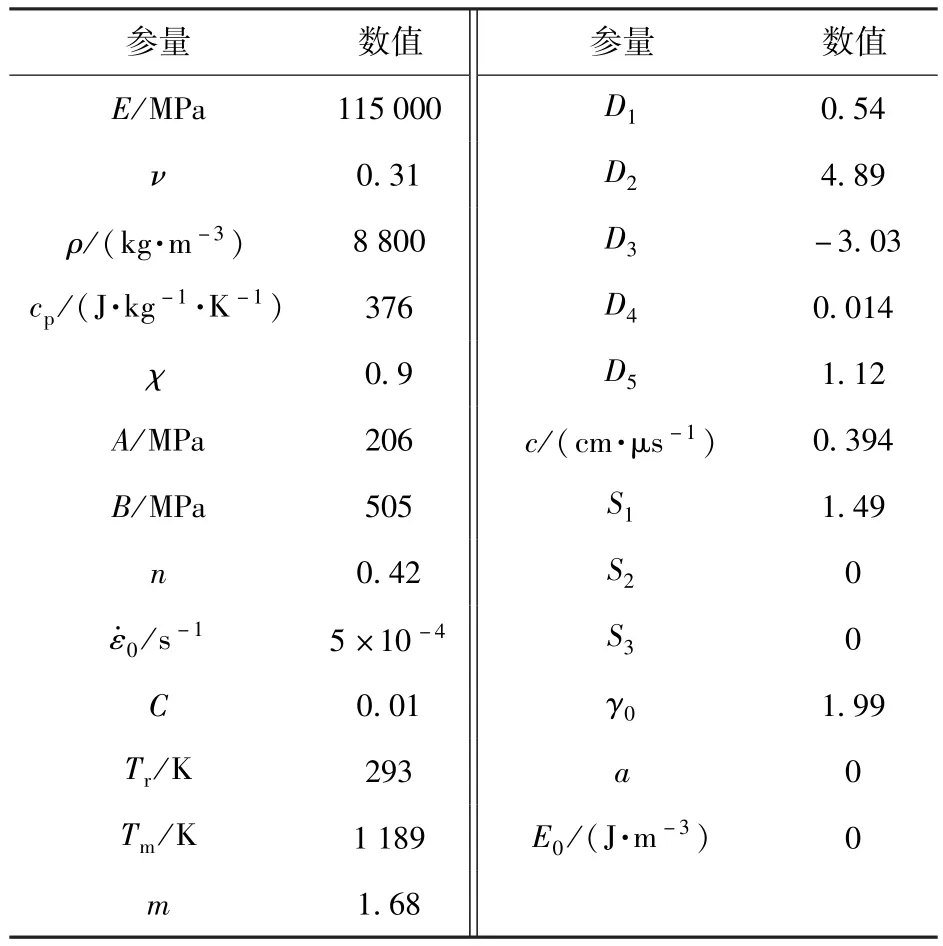
表1　弹带材料模型参数Tab.1 Material parameters of rotating band

2.3接触算法及摩擦系数

弹带与身管内壁的接触算法采用LS-DYNA中基于罚函数法的侵蚀接触算法。

根据文献［1］的研究，弹带与身管内壁之间采用库伦摩擦模型，动摩擦系数取为0.1.

2.4载荷与边界条件

弹底压力ps是弹丸所受到的最主要作用力，是推动弹丸向前运动的动力。为确定挤进压力等内弹道参量，还应知道弹后火药燃气的平均压力。通过实弹射击测试得到该大口径榴弹炮发射时的膛底压力变化曲线，由文献［17］第1.5.5节以及第3.4.5节所述内弹道计算中应用的压力换算关系，换算得到弹底压力和平均压力变化曲线，如图2所示。基于弹丸本体为刚体及不考虑弹丸动不平衡的假设，模型计算中将弹底压力与弹底面积乘积所得的合力作为弹带挤进数值模拟的主动载荷，作用在弹丸本体上，方向与炮膛轴线同轴。根据模型假设2和假设3，边界条件是约束火炮身管的全部自由度。

3　弹带挤进过程数值计算与结果分析

3.1弹带变形及刻槽形成过程

利用LS-DYNA 971软件对所建立的弹带挤进过程有限元模型进行数值计算，弹带在7.6 ms完全挤进全深膛线。图3为弹带挤进过程中不同时刻von Mises应力云图，也显示了弹带的变形形态。从中可以看出，弹带材料在挤进过程中产生了塑性硬化和大变形，且被膛线挤压导致材料失效形成刻槽，与实弹射击后回收的弹丸弹带变形情况一致，如表2所示。

图2　弹底压力与平均压力曲线Fig.2 Projectile base pressure and chamber pressure

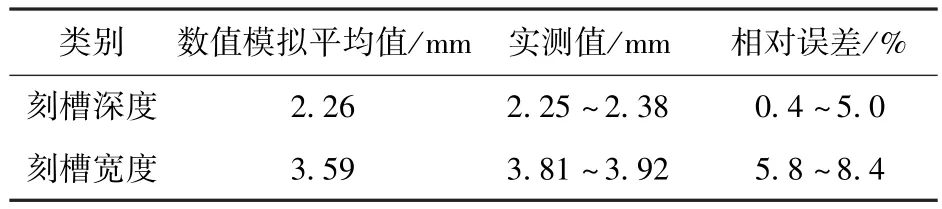
表2　数值模拟与实测弹带刻槽尺寸对比Tab.2 Comparison of calculated and experimental groove sizes

为了理解弹带的刻槽形成过程，还应研究弹带材料在经历大塑性变形之后的断裂失效模式。通过考查弹带材料断裂失效区域的应力应变状态，来判断弹带刻槽形成过程中的韧性断裂机制。如图4和图5所示，分别为弹带后端到达膛线起始部时刻（t= 6.9 ms）弹带材料的应力三轴度与Lode角参数云图。结果显示，在挤进过程中，弹带材料在直接受膛线作用的断裂失效区域应力三轴度主要为负值，Lode角参数也主要为负值，表明挤进过程中弹带的韧性断裂以剪切失效为主导，弹带材料内部主要处于受压状态。弹带前、后端面附近材料由于膛壁的摩擦力作用，应力三轴度为正值，主要承受拉伸作用。

类似地，图6给出了弹带材料内部等效塑性应变云图，结合图3、图4和图5，可以推断弹带在挤进过程中的材料变形流动及刻槽形成机理。挤进时，弹带材料逐层发生挤压和塑性变形，随着挤进的深入，弹带径向的过盈部分受膛线剪切被推挤到弹带后方，与阳线相对的弹带材料被膛线挤压和剪切后，一部分被推挤到弹带后方，另一部分逐渐挤入阴线。图6还表明，挤进后的弹带剖面体现出较为明显的层状变形特征，其内部区域的塑性变形量很小，与文献［18］和文献［19］实验研究中对弹带膛内塑性变形机理的推测相符。

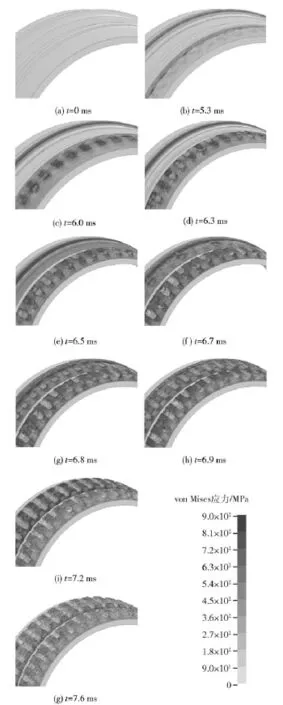
图3　弹带挤进过程中的von Mises应力Fig.3 Evolution of von Mises stress for rotating band

图4　弹带内部应力三轴度Fig.4 Stress triaxiality of rotating band

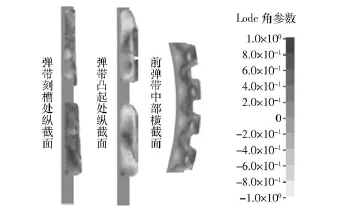
图5　弹带内部Lode角参数Fig.5 Lode angle parameters of rotating band

图6　弹带内部等效塑性应变Fig.6 Effective plastic strain of rotating band

挤进终了时，弹带总塑性变形量达到最大，其绝热变形引起的温升也达到最大。图7所示为该时刻弹带绝热变形温度分布图，其最高温度小于弹带材料熔点1 189 K.从中可以看出，对于本文弹带挤进问题，弹带绝热变形产生的热量不足以使弹带材料熔化，在挤进过程中弹带没有发生熔融。

3.2挤进过程中弹丸的运动规律

如图8（a）、图8（b）和图8（c）所示，分别为计算得到的挤进过程中弹丸的位移-时间、速度-时间和加速度-时间曲线。根据表3所列出的弹带挤进时期主要参数计算结果，最大挤进阻力点弹丸运动速度为66.7 m/s，符合文献［3］中大约在30～50 m/s甚至更高一些的论述。此外，图8中还给出了不考虑摩擦的弹带挤进过程中弹丸运动规律以供对比。

图7　弹带绝热变形温度分布图Fig.7 Temperature profile of rotating band under adiabatic deformation

3.3弹带的动态挤进阻力

弹带挤进坡膛，产生塑性变形阻力，其与摩擦阻力合成弹带挤进时期的弹丸运动阻力。根据弹丸运动微分方程，计算弹带的动态挤进阻力R（t），

式中：S为弹底面积；ps（t）为弹底压力；mp为弹丸质量；为弹丸加速度。

将计算所得随时间变化的弹带动态挤进阻力换算成随弹带挤进行程变化，如图9所示。最大挤进阻力值及其对应的时刻列于表3中，从中可以看出，最大挤进阻力出现在弹带完全挤进全深膛线之前。计算结果显示，弹带动态挤进阻力变化曲线与文献［1-3］经典理论中准静态模型或简化动态模型的挤进阻力曲线有较大差别。

从图9中可以看出，弹底压力增加到一定值后，迫使弹丸向前加速运动，使弹带产生塑性变形挤进膛线。随着弹带挤入坡膛长度增加，弹带塑性变形量增大乃至发生断裂失效，阻力迅速上升。当弹带变形量不再增加，阻力保持不变。而后，弹带变形量不断减小，阻力则逐渐下降。此后，弹带已被刻成与膛线相吻合的沟槽，阻力迅速下降至沿膛线运动的摩擦阻力值。

作为对比，图9中也给出了不考虑摩擦的弹带动态挤进阻力曲线。结果表明，在挤进过程的初期，由于弹带凸台的作用，弹带与坡膛的接触面积较小，挤进阻力中弹塑性变形阻力占主导，因而该阶段摩擦系数对挤进阻力的影响不大。随着弹带挤进深度增加，弹带发生塑性变形和材料流动，其与坡膛接触面积迅速增大，摩擦阻力所占比重相应增大，所以该阶段摩擦系数对挤进阻力有显著影响。

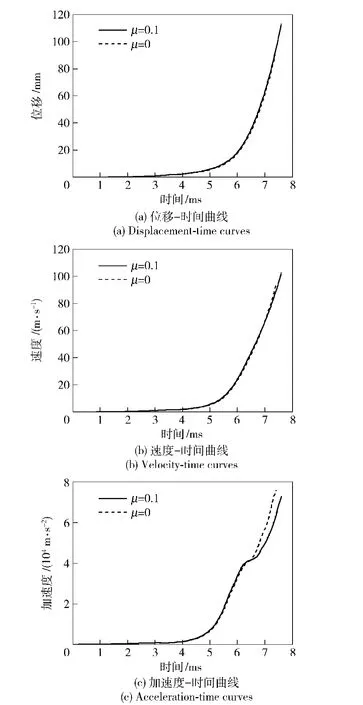
图8　弹丸运动曲线Fig.8 Motion curves of projectile

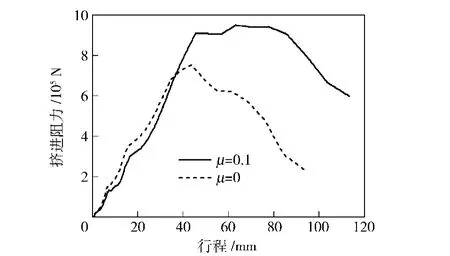
图9　弹带动态挤进阻力Fig.9 Dynamic engraving resistances

3.4挤进压力的确定

弹带全部挤进坡膛，弹带挤进阻力达到最大值，与之相应的弹后火药燃气平均压力称为挤进压力。由图9可以知道弹带动态挤进阻力达到最大值的时刻，该时刻在图2中所对应的火药燃气平均压力值即为挤进压力，其数值也列于表3中。结果表明，动态计算所得弹带挤进压力226.5 MPa，比经典内弹道理论中挤进压力取值30 MPa大得多。文献［17］中提到奥波波可夫研究发现某76 mm火炮的挤进压力达到173 MPa，为最大膛压的65%.文献［20］针对截短身管30 mm火炮进行了挤进实验测试研究，其挤进压力在6/7装药下为160～200 MPa，在7/14装药下为130～170 MPa.文献［21］测试得到射击情况下采用铜弹带的海30舰炮弹丸挤进压力为209 MPa，计算值为201.3 MPa.从中可以看出，本文动态条件下挤进压力计算结果与这些文献报道在数量级上相当，但是由于所研究火炮对象不同，具体数值有差异。

表3　弹带挤进时期主要参数计算结果Tab.3 Calculated results of rotating band engraving process

4　结论

本文对某大口径榴弹炮发射条件下弹带挤进过程中的弹带动态挤进阻力、挤进压力、弹带大变形和弹丸运动规律进行了数值模拟研究。结果表明：

1）挤进过程中弹带材料经历塑性变形流动，发生剪切失效占主导的韧性断裂并形成刻槽。弹带挤进后具有明显的层状特征，其内部区域的塑性变形量很小。弹带绝热变形产生的热量不足以使弹带材料熔化，弹带在挤进过程中没有发生熔融。

2）弹带动态挤进阻力变化规律与经典理论中准静态模型或简化动态模型的挤进阻力曲线有较大差别，最大挤进阻力为9.51×105N.

3）弹带挤进压力为226.5 MPa，比经典内弹道理论中挤进压力取值30 MPa大得多。与之对应时刻的弹丸速度为66.7 m/s.

本文工作为研究弹丸膛内运动初始条件及后续探索挤进时期更复杂膛内现象提供了一个可供参考的数值模拟研究方法。受限于当前条件，文中用到的实验测试数据虽然为数值模拟研究提供了支持，但不能直接验证弹带动态挤进阻力及弹丸运动规律的计算结果。下一步工作的重点是开展针对弹带动态挤进阻力及弹丸运动规律的实验研究。

（

）

［1］丘尔巴诺夫E B.挤进时期内弹道学与挤进压力计算［M］.杨敬荣，译.北京：国防工业出版社，1997. Qierbarov E B.Interior ballistics and engraving force calculation during engraving of projectile［M］.YANG Jing-rong，translated. Beijing：National Defense Industry Press，1997.（in Chinese）

［2］周彦煌，王升晨.实用两相流内弹道学［M］.北京：兵器工业出版社，1990. ZHOU Yan-huang，WANG Sheng-chen.Practical two-phase flow interior ballistics［M］.Beijing：Publishing House of Ordnance Industry，1990.（in Chinese）

［3］张喜发，卢兴华.火炮烧蚀内弹道学［M］.北京：国防工业出版社，2001. ZHANG Xi-fa，LU Xing-hua.Interior ballistics of erosion guns［M］. Beijing：National Defense Industry Press，2001.（in Chinese）

［4］Tao C，Zhang Y，Li S，et al.Mechanism of interior ballistic peak phenomenon of guns and its effects［J］.Journal of Applied Mechanics，2010，77（5）：051405.

［5］Chen P C.Analysis of engraving and wear in a projectile rotating band，ARCCB-TR-99012［R］.Watervliet，NY，US：US Armament Research，Development and Engineering Center，1999.

［6］Keinänen H，Moilanen S，Toivola J，et al.Influence of rotating band construction on gun tube loading—part I：numerical approach［J］.Journal of Pressure Vessel Technology，2012，134（4）：041006.

［7］Toivola J，Moilanen S，Tervokoski J，et al.Influence of rotating band construction on gun tube loading—part II：measurement and analysis［J］.Journal of Pressure Vessel Technology，2012，134（4）：041007.

［8］Balla J，Jankovych R，Duong V Y.Interaction between projectile driving band and forcing cone of weapon barrel［C］∥Proceeding of the Applied Computing Conference.Angers，France：IASME/ WSEAS，2011：17-19.

［9］樊黎霞，何湘玥.弹丸挤进过程的有限元模拟与分析［J］.兵工学报，2011，32（8）：963-969. FAN Li-xia，HE Xiang-yue.Finite element simulation and process analysis of projectile entering into barrel［J］.Acta Armamentarii，2011，32（8）：963-969.（in Chinese）

［10］孙河洋，马吉胜，李伟，等.坡膛结构变化对弹带挤进过程影响的研究［J］.振动与冲击，2011，30（3）：30-33. SUN He-yang，MA Ji-sheng，LI Wei，et al.Influence of different bore structures on engraving process on projectile［J］.Journal of Vibration and Shock，2011，30（3）：30-33.（in Chinese）

［11］孙河洋，马吉胜，李伟，等.坡膛结构变化对火炮内弹道性能影响的研究［J］.兵工学报，2012，33（6）：669-675. SUN He-yang，MA Ji-sheng，LI Wei，et al.Study on influence of bore structure on gun's interior ballistic performances［J］.Acta Armamentarii，2012，33（6）：669-675.（in Chinese）

［12］Hallquist J O.LS-DYNA keyword user's manual［M］.Livermore，CA：Livermore Software Technology Corporation，2014.

［13］South J，Power B，Minnicino M.Evaluations of computational techniques for the engraving of projectiles［J］.WIT Transactions on Modelling and Simulation，Computational Ballistics III，2007（45）：193-202.

［14］Johnson G R，Cook W H.A constitutive model and data for metals subjected to large strains，high strain rates and high temperatures［C］∥Proceedings of the 7th International Symposium on Ballistics.Hague，the Netherlands：IBC，1983：541-547.

［15］Johnson G R，Cook W H.Fracture characteristics of three metals subjected to various strains，strain rates，temperatures and pressures［J］.Engineering Fracture Mechanics，1985，21（1）：31-48.

［16］Meyers M A.Dynamic behavior of materials［M］.New York：John Wiley&Sons，1994.

［17］金志明.枪炮内弹道学［M］.北京：北京理工大学出版社，2004. JIN Zhi-ming.Interior ballistics of guns［M］.Beijing：Beijing Institute of Technology Press，2004.（in Chinese）

［18］殷军辉，郑坚，倪新华，等.弹丸膛内运动过程中弹带塑性变形的宏观与微观机理研究［J］.兵工学报，2012，33（6）：676-681. YIN Jun-hui，ZHENG Jian，NI Xin-hua，et al.Research on macroscopic and microscopic mechanism of plastic deformation of bearing band［J］.Acta Armamentarii，2012，33（6）：676-681.（in Chinese）

［19］Yin J H，Zheng J，Jia C Z，et al.Plastic deformation and surface recrystallization of Cu-4 mass%Zn alloy under instantaneous extrusion and high speed friction［J］.Key Engineering Materials，2011，467/468/469：1280-1284.

［20］曾思敏，童伟民，焦化南.弹丸挤进过程的测试研究［J］.兵工学报，1991，12（4）：71-74. ZENG Si-min，TONG Wei-min，JIAO Hua-nan.Measurement of the engraving process of projectiles［J］.Acta Armamentarii，1991，12（4）：71-74.（in Chinese）

［21］何勇.挤进过程实验研究［J］.弹道学报，1996，8（4）：33-36. HE Yong.The experimental research of engraving process［J］. Journal of Ballistics，1996，8（4）：33-36.（in Chinese）

Numerical Research on Rotating Band Engraving Process of a Large-caliber Howitzer

SUN Quan-zhao，YANG Guo-lai，WANG Peng，GE Jian-li，XIE Run
（School of Mechanical Engineering，Nanjing University of Science and Technology，Nanjing 210094，Jiangsu，China）

A finite element model of the rotating band engraving into the forcing cone section of gun tube is established to explore the mechanism of engraving process of rotating band of a large-caliber howitzer under launch conditions.The dynamic engraving process of the rotating band is studied through numerical simulation，and the maximum resistance，engraving pressure and projectile velocity at the corresponding time are obtained.The deformation and groove formation processes of the rotating band are analyzed.The dynamic engraving resistance of the rotating band，the engraving pressure and movement of projectile are also calculated.The calculated results show that the rotating band undergoes plastic deformation and material flow，and forms the grooves on it due to ductile fracture，where shear failure is dominant.The rotating band has a layered feature after engraving，and the plastic strain in the band is small.The heat generated by adiabatic deformation of the rotating band is not enough to melt it.The simulation results of the deformation of the rotating band show good agreement with the test data from the recovered projectile.

ordnance science and technology；engraving of rotating band；deformation of rotating band；engraving resistance；engraving pressure；finite element simulation

TJ301

A

1000-1093（2015）02-0206-08

10.3969/j.issn.1000-1093.2015.02.003

2014-04-29

国家重点基础研究发展计划项目（51319702）；国家自然科学基金项目（11172139）

孙全兆（1987—），男，博士研究生。E-mail：sunquanzhao@hotmail.com；杨国来（1968—），男，教授，博士生导师。E-mail：yyanggl@mail.njust.edu.cn