两种供应模式下备件协同订购策略优化研究

王慎，李庆民，李华，阮旻智

（1.海军工程大学兵器工程系，湖北武汉430033；2.海军91115部队，浙江舟山316000；3.海军工程大学科研部，湖北武汉430033）

两种供应模式下备件协同订购策略优化研究

王慎1，2，李庆民3，李华1，阮旻智3

（1.海军工程大学兵器工程系，湖北武汉430033；2.海军91115部队，浙江舟山316000；3.海军工程大学科研部，湖北武汉430033）

备件保障系统补充库存时，除实施常规补给外，还会采用紧急订购满足备件短缺需求，以减少装备故障停机时间。针对上述两种供应模式下多站点订购策略联合优化问题，建立了以复合备件满足率为约束、单位时间期望成本为目标函数的协同订购解析模型；基于拉格朗日因子和策略迭代方法，给出了一种启发式优化算法。为模拟备件保障过程，建立了相应蒙特卡罗仿真模型，并将解析模型优化结果与遗传算法优化的仿真模型进行了对比。结果分析表明，解析模型不仅能够提供近似最优解，而且具有良好的运算效率。

运筹学；备件；协同订购；库存；优化

0　引言

随着军事装备自动化、集成化要求不断提高，装备故障停机往往造成昂贵的损失，因此对于备件短缺后延迟供应时间的要求越来越短，仅靠从上级站点常规补给的方法已经无法满足任务执行需要。相关资料显示，在3种主要停机因素中，等待备件所造成的停机时间已经超过修复性维修和预防性维修停机的总时间，成为制约装备战备完好性提高的瓶颈［1］。这就需要装备使用现场除平时向后方仓库进行常规订购外，还应在库存备件短缺时，由应急保障站点进行紧急补货，以减少装备停机带来的经济及机会损失，即实施常规补给依靠后方仓库、库存不足时由应急保障站点紧急供应的复合式备件保障策略。

与常规补给相比，紧急供应需要增加保障设施，具有较短的订购提前期和额外的成本。目前，针对该模式下的备件订购问题，国内外学者已进行了一定研究。Moinzadeh等［2］针对连续检查策略下单级库存系统，第一次提出了常规补给及紧急供应中再订购点和再订购量的联合优化问题，并使用枚举法进行求解；Johansen等［3］在最多只有一个未交付常规订单的假设下，将净库存量及未交付订单剩余时间作为系统状态，采用半马尔可夫决策过程对紧急供应的订购策略进行优化；Axsater［4］放宽Johansend模型中假设条件，给定常规补给再订购点和再订购量，采用启发式算法求解紧急订购的触发条件和订购数量。Van Wijk等［5］、Howard等［6］指出可根据备件短缺发生的规律，选取恰当的紧急订购启动时机，预防常规补给交付前库存不足事件的发生。Kranenburg等［7］在库存部分共享的假设下，对同级站点间紧急横向转运问题展开研究；Kutanoglu等［8］、Purnomo等［9］放宽可修复备件控制多级技术（METRIC）中仅有一个供货站点的假设，建立了横向库存调整和后方补货两种紧急供应模式并存的多渠道库存模型。上述文献将应急保障站点当作无限备件源，仅对单个站点订购策略或同级站点间库存横向调整问题进行了研究。在供应链协同订购优化方面，Axsater等［10］建立了两级库存系统再订购点协同优化模型。阮旻智等［11］在随机延误时间假设下，对多站点备件协同订购模型进行了研究。王慎等［12］在串件拼修条件下，对备件维修供应系统中库存动态配置管理问题展开研究。上述文献仅考虑了常规补给下多级保障系统库存协同控制问题。

尽管国内外学者在相关领域已取得了一些研究进展，但在建立模型时仅考虑多供应模式、多等级、多参数等因素中某一方面，而工程实践中这些因素往往是共同出现的。比如，应急保障站点对多个基层级站点提供紧急补货服务时，自身也需要向后方仓库进行备件订购；某个基层级站点的订购策略选择会影响到应急保障站点的库存状态，进而影响到其他基层级站点的服务水平。这就需要在管理人员在确定库存控制参数时，考虑整个保障系统内订购策略的耦合关系。为解决该问题，本文针对后方仓库、应急保障站点及装备使用现场组成的备件供应系统，在常规补给与紧急补货两种供应模式下，对多级站点再订购点、再订购量联合优化问题展开研究。

1　问题描述及假设

基层级（装备使用现场）、中继级（应急保障站点）、后方仓库组成的备件保障系统如图1所示。设任一基层级站点j的备件需求率服从参数为λj的泊松分布，采用常规供应依靠后方仓库、备件短缺时由中继级紧急补货的复合式订购策略：定义库存水平IL为“现有库存OH+待收订单-备件短缺数”。基层级j在日常运作中连续检查自身库存水平ILj，当ILj随备件消耗下降至再订购点Rj时，向后方仓库发出订购量为Qj的备件需求；订购提前期内若发生现有库存不足（OHj＜0）事件，则立刻向中继级发送补货申请，中继级在现有库存大于0时就以紧急供应模式将备件发送到相应站点。在保障基层级站点的同时，中继级也采用（R0，Q0）的订购策略，当库存水平IL0下降到R0时，向后方仓库发出订购量为Q0的订购申请。设后方仓库的库存量足够大，不会因库存不足而产生补给延误，基层级备件消耗及订购过程示意如图2所示。

在上述过程中，虽然由基层级站点看来，被紧急供应满足的需求同样是在本站点延迟交付，但从常规供应管理者角度，这些需求已经转运到中继级，不再由未来的常规订单满足。因此，在建立各站点（R，Q）策略时，基层级库存水平定义为“现有库存+待收常规订单”，不考虑备件短缺数和未交付紧急供应订单；中继级库存水平仍为“现有库存+待收订单-备件短缺数”。

2　成本及满足率模型

协同订购策略优化的目标是在服务水平指标约束下，合理规划各级站点订购方案，令系统长期运行费用最低。备件满足率是指单位时间内库存满足需求数与总需求量之比的期望值，是衡量备件供应服务水平的典型指标［1］。本节首先以联合订购策略为优化变量，分别建立系统及各级站点的单位时间期望成本和基层复合满足率模型。可表示为

式中：（R0，Q0）表示中继级站点的订购策略；（Rj，Qj），j=1，…，N为N个基层级站点的订购策略。设G、g0、gj分别为系统、中继级、基层级的单位时间期望成本。因基层级与中继级订购策略相互耦合，从而g0为所有站点订购策略的函数，则G可表示为

基层级平时消耗库存备件，库存不足时由中继级紧急补货。因此，基层复合满足率EFR定义为单位时间内自身库存、紧急供应满足需求的比率，同样为的函数。设ωj（Rj，Qj）为基层库存满足率、为中继库存满足率，易知基层复合满足率可表示为

下面对（2）式与（3）式中基层及中继级成本、满足率计算公式进行推导。

图1　多级备件保障系统Fig.1 Multi-echelon support system for spare parts

图2　基层级备件消耗及订购过程Fig.2 Demand and ordering process of spare parts in base site

2.1基层级成本及满足率计算

规定基层级j订购策略满足Rj＜Qj的约束条件，则由第1节中基层级备件消耗、订购过程及泊松需求可知，基层级库存水平是以Rj+Qj为常返态的更新过程。相邻两次Rj+Qj状态之间的时间为一个订购周期。根据更新过程理论，只需以订购周期内参数期望值为研究对象，即可求得基层级成本和满足率的计算公式。

订购周期可分为备件消耗期和订购提前期两个阶段。备件短缺事件仅会发生在订购提前期内。发生备件短缺时，需求将转运至中继级。设基层级j常规订购提前期为Lj，提前期内紧急供应的备件期望数为ELS（Rj）.因基层级需求服从参数为λj的泊松分布，则ELS（Rj）可由（4）式计算：

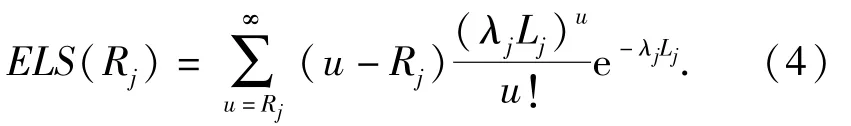
根据ELS（Rj），可得订购周期初始时刻的现有库存期望值E（OHj）表达式为

因订购周期初始时刻的现有库存与订购周期内总需求相互独立，订购周期初始时刻交付的备件中单件产品的平均持有时间可表示为E（OHj）/λj+ Qj/2λj.因此，订购周期内的期望库存持有成本EHC即为

设pj为单个产品单位时间短缺造成的损失，为紧急供应产生的固定费用（运输、管理成本等），tj为紧急供应需要的备件等待时间，则单个产品紧急供应费用πj可表示为

设hj为单个产品单位时间库存持有费用，Aj为固定订购费用，则基层级站点j订购周期内期望成本Cj（Rj，Qj）可表示为

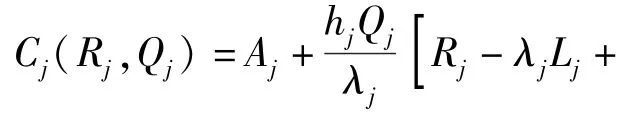
因订货周期内的期望需求数为Qj+ELS（Rj），则订购周期期望长度Tj（Rj，Qj）可表示为

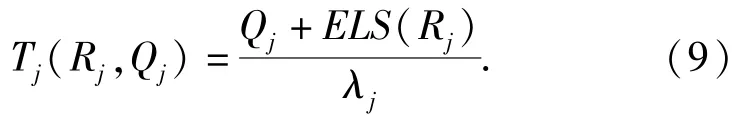
根据更新过程理论可知，库存站点单位时间期望成本gj（Rj，Qj）可表示为订购周期内期望成本Cj（Rj，Qj）与订购周期期望长度Tj（Rj，Qj）之比，即

由gj（Rj，Qj）定义可知，gj（Rj，Qj）中因需求转运至中继级造成的损失为“πj×基层j单位时间内平均缺货数”。将该值除以“πj×基层j单位时间内平均需求数”，即为（Rj，Qj）策略下基层库存保障失败的比例。而gj（Rj，Qj）中紧急供应费用可分离为bj·ELS（Rj）/Tj（Rj，Qj），因此基层库存满足率ωj（Rj，Qj）表示为

2.2中继级成本及满足率计算

基层级在库存不足时，会将需求发送至中继级。建模时将这一备件申请过程近似为泊松过程，则中继级备件需求率λ0可表示为

从装备使用角度出发，中继级备件短缺不会直接产生损失，其损失是因基层级短缺而间接产生的。中继级发生的备件短缺中，只有一定比例会对基层级j产生影响，其计算公式为

因此，中继级单个产品单位时间内短缺损失p0可表示为

在上述近似下，中继级站点可用单站点（R，Q）策略下库存模型进行建模。定义中继级净库存NI0为“现有库存-备件短缺数”，设IL0为中继级库存水平、L0为订购提前期，则在稳态情况下有

（15）式中D（L0）为订购提前期内备件需求数，则在IL0=n条件下有

设C0（n）为IL0=n条件下单位时间内库存持有及短缺成本、h0为单个产品单位时间内持有费用，则

稳态情况下IL0满足［R0+1，R0+Q0］上的均匀分布，设g0（R0，Q0）为中继级单位时间内期望成本，则

需求近似为泊松过程，则中继级库存满足率ω0等于中继级净库存大于0的概率［3］，即

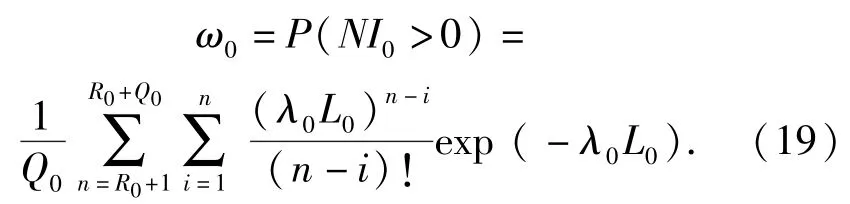
至此，将（1）式～（19）式联立，即可得到保障系统单位时间期望成本及基层级复合满足率计算公式。

3　模型优化算法

3.1协同订购策略优化

由（3）式可知，当中继级满足率ω0给定时，基层级站点j订购策略选择将不会影响到其他站点的复合满足率。因此，分两个阶段对模型进行迭代求解：首先给定中继级满足率为，在基层库存满足率ωj约束下，以各站点成本函数最小化为目标，分别求得各站点最优策略；其次，将前一阶段得到的最优策略作为各站点订购策略，以为约束，求得此时中继级最优策略（R0， Q0）及系统总成本，并与上轮计算的系统成本比较，较小值对应各站点策略即为当前最优策略。循环迭代上述过程，直至遍历完ω0的全部取值范围。

设ηmax=max（η1，η2，…，ηN），则根据（3）式有ω0＞ηmax时各基层站点自身库存满足率ωj=0，即此时各站点不存储备件完全依靠中继转运。由此可知ω0的取值范围不会超过ηmax.选取恰当的增量Δω0后，具体优化算法如下所示：

3.2基层级策略优化

协同订购策略优化算法步骤2中任一基层站点策略优化问题，利用（3）式可转化为如下模型（各站点解法相同，下文不再出现标识站点的角标j）：

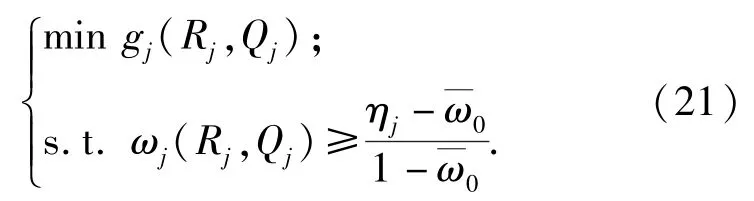
因满足率ω为紧急供应费用π的单调不减函数，可采用以下拉格朗日方法求解该问题：设π0为基层级规定的紧急供应费用，忽略约束条件，计算π（1）=π0时的最优策略（R（1），Q（1））；将（R（1），Q（1））代入（11）式，检查当前满足率是否达到约束条件；若未达到，增加转运费用至π（2），再次计算π（2）下最优策略（R（2），Q（2））.重复上述过程，直至找到满足约束条件的最小转运费π（n）.该方法的关键是“如何以g（R，Q）最小为目标，对再订购点R和订货量Q进行联合优化求解”。

3.2.1无约束下优化算法

基层级在现有库存为0时，会将需求转运至中继级。因此可将基层级站点当作缺货不补原则下的（R，Q）库存模型。当前对于这类模型在泊松需求下的优化虽然结果精确，但建模复杂、运算效率低［3］。为此，本节基于半马尔可夫决策过程中策略迭代优化思想，提出一种简便的求解方法。设当前策略为（RN，QN）、期望成本为gN，定义策略改善函数TgN（R，Q）为

若策略（R*，Q*）满足：

则有g（R*，Q*）≤gN.为构造满足（23）式的策略，可令（R*，Q*）满足：

此时有

即g（R*，Q*）≤gN.为此，对TgN（R，Q）分别关于R和Q求偏导，并令其等于0，可得

在上述讨论的基础上，给出如下求解步骤：

1）选择初始策略（RN，QN），根据（11）式求出gN；

2）将QN、gN代入（25）式，求出相应R值，设其为R*；

3）将R*、gN代入（26）式，求出相应Q值，设其为Q*；

4）利用（11）式，计算g*=（R*，Q*）.设e为指定误差容限，如果|g*-gN|≤e，则迭代停止；否则，令RN=R*，QN=Q*，gN=g*，返回步骤2.

3.2.2满足率约束下优化算法

因满足率ωπ是π的单调不减函数，可以从π0开始逐渐增加转运费用π，在不同转运费用下使用3.2.1节迭代方法获得最优策略，直至所得策略满足约束条件。从实际计算过程可知，当转运费用改变量较小时，从上一轮转运费用的最优策略开始，只需很少的迭代次数就可以找到当前优化策略。具体算法如下所示：

1）令转运费用π=π0，选择费用增量Δπ；

2）选择（RN，QN）为初始策略，使用3.2.1节迭代算法寻找最优策略；

4　仿真模型

基于离散事件仿真工具ExtendSim，建立两种供应模式下多级协同订购仿真模型，对不同订购方案进行对比分析。基层级仿真处理流程如图3所示，仿真开始时，根据的输入值，以服从［R+1， R+Q］均匀分布的随机数，初始化各站点库存水平IL、净库存量NI.仿真过程中，以Create模块模拟基层站点需求，用Unbatch模块将需求信号拆分为两个线程：每次需求到来时，常规供应线程检查当前库存水平，在下降到R时发出订购量为Q的订购申请；紧急订购线程检查现有库存，在小于0时将需求转运至中继级。

图3　基层级模块仿真处理流程Fig.3 Simulation flow chart of base site module

模型以站点单位时间成本之和、备件满足率为输出。单个站点成本采用以下方法计算：用Value库中DBread模块读取当前库存状态OH、向后方订购次数OrderNum、向中继转运次数TransNum，用Simulation Variable模块读取当前仿真时间TN，可得单位时间成本统计公式为

同理，用DBread模块读取站点j的库存满足需求数Self_FillNum、中继级满足站点j的需求数Trans _FillNum、站点j的总需求数TotalNum，则站点j的复合满足率EFRj统计公式为

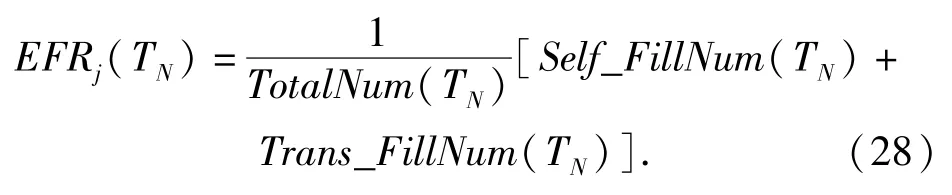
5　仿真实验

以图1所示的保障系统为例，采用仿真实验方法对所建解析模型进行验证分析，首先进行实验参数设计。规定中继级订购提前期L0=5 d，库存持有费用h0=1 000元，固定订购费用A0=4 000元；5个基层级站点为同型站点，其备件需求率λj= 0.25个/d，库存持有费用hj=1 000元，短缺费用pj=1 500元。在以上参数相同的情况下，为基层级订购提前期Lj、紧急供应费用πj、固定订购费用Aj、复合满足率下限ηj等4个影响订购方案较大的参数选择两个试验水平，最终形成一个四因素两水平的全面实验方案，因素水平表如表1所示。

表1　因素水平表Tab.1 Factors and levels

分别将每个输入参数组合代入解析模型和仿真模型进行计算。其中，仿真模型采用遗传算法优化，对各种可能订购方案进行300次仿真，以收敛度0.95为结束条件。两种模型在16组参数下的计算结果如表2所示。设GA、GE分别为解析、仿真优化后系统单位时间期望成本，EFRA、EFRE分别为解析、仿真优化后基层平均复合满足率，则有成本相对误差ΔG=（GA-GE）/GE，满足率误差ΔEFR= EFRA-EFRE.二者在多次实验中的变化情况如图4所示，分析结果如表3所示：最大偏差不超过2.5%，证明了解析模型的正确性。

上述实验运行在酷睿I3、内存4 G的台式机上，解析模型平均运行时间为7.1 min，仿真模型平均优化时间为20.3 min.解析模型效率提升约185%，相比仿真方法能够有效缩短运行时间，且不会出现仿真优化中站点增多造成的组合爆炸问题，具有较好的工程实用性。

表2　不同输入参数下两种模型优化结果对比Tab.2 Comparison of optimal solutions of the two models with different parameters

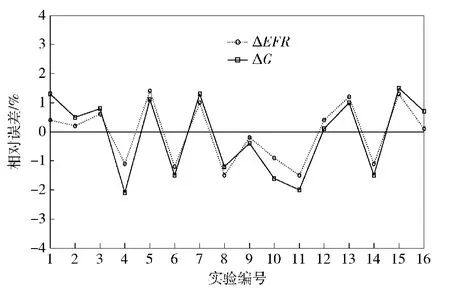
图4　不同输入参数下模型误差Fig.4 Errors of analytical model with different parameters

表3　成本及满足率误差分析Tab.3 Error analysis of cost and fill rate%

6　结论

本文针对两种供应模式下备件协同订购问题，首先以联合订购策略为变量，分别建立了单位时间成本和满足率的计算模型；以中继级满足率为拉格朗日因子，解除约束条件中的站点耦合关系，采用策略迭代算法对模型进行优化求解。为模拟备件保障过程，同时评估不同订购方案效能，建立了基于ExtendSim平台的协同订购仿真模型。对比解析模型和仿真模型的优化结果可知：所建解析模型及优化算法除精度满足工程需要外，还具有较高的运算效率。以本文实验为例，解析模型成本平均相对误差为1.16%，复合满足率平均误差为0.88%，最大值不超过2.5%；平均运行时间为7.1 min，相比仿真优化算法（20.3 min），运行时间减少约2倍，当站点较多时，这一优势更加突出。

文中模型丰富了装备综合保障理论，能够为复杂备件保障系统的协同订购问题提供决策支持，具有一定的工程实用价值。

（

）

［1］Sherbrooke C C.Optimal inventory modeling of system：multi-echelon techniques［M］.2nd ed.Boston：Artech House，2004：21-22.

［2］Moinzadeh K，Nahmias S.A continuous review model for an inventory system with two supply modes［J］.Management Science，1988，34（6）：761-767.

［3］Johansen S G，Thorstenson A.An inventory model with Poisson demands and emergency orders［J］.International Journal of Production Economics，1998，56（3）：275-289.

［4］Axsater S.A heuristic for triggering emergency orders in an inventory system［J］.European Journal of Operational Research，2007，176（2）：880-891.

［5］Van Wijk A C C，Van Houtum G J.Optimal allocation policy for a multi-location inventory system with a quick response warehouse［J］.Operations Research Letters，2013，41（3）：305-310.

［6］Howard C，Reijnen I C，Marklund J.Using pipeline information in a multi-echelon spare parts inventory system［R］.Sweden：Lund University and Eindhoven Technical University，2010：12-13.

［7］Kranenburg A A，van Houtum G J.A new partial pooling structure for spare parts networks［J］.European Journal of Operational Research，2009，199（3）：908-921.

［8］Kutanoglu E，Mahajan M.An inventory sharing and allocation method for a multi-location service parts logistics network with time-based service levels［J］.European Journal of Operational Research，2009，194（3）：728-742.

［9］Purnomo A.Multi-echelon inventory model for repairable item emergency with lateral transshipment in retail supply chain［J］. Australian Journal of Basic and Applied Sciences，2011，34（1）：462-474.

［10］Axsater S，Howard C，Marklund J.A distribution inventory model with transshipments from a support warehouse［J］.IIE Transactions，2012，45（3）：309-322.

［11］阮旻智，李庆民，黄傲林.（R，Q）库存策略下消耗件的协同订购方案优化［J］.北京理工大学学报，2013，33（7）：680-684. RUAN Min-zhi，LI Qing-min，HUANG Ao-lin.Optimization of cooperative ordering project for consumable spare parts under（R，Q）inventory policy［J］.Transactions of Beijing Institute of Technology，2013，33（7）：680-684.（in Chinese）

［12］王慎，李庆民，彭英武.串件拼修对策下两级备件维修供应系统动态管理模型［J］.航空学报，2013，34（6）：1326-1335. WANG Shen，LI Qing-min，PENG Ying-wu.Dynamic management model of two-echelon maintenance supply system for spare parts with cannibalization［J］.Acta Aeronautic et Astronautica Sinica，2013，34（6）：1326-1335.（in Chinese）

Optimal Cooperative Ordering Policy for Spare Parts Inventory with Two Supply Modes

WANG Shen1，2，LI Qing-min3，LI Hua1，RUAN Min-zhi3
（1.Department of Weaponry Engineering，Naval University of Engineering，Wuhan 430033，Hubei，China；2.the 91115th Unit of PLA，Zhoushan 316000，Zhejiang，China；3.Office of Research and Development，Naval University of Engineering，Wuhan 430033，Hubei，China）

In order to satisfy the demands of inventory system on the spare parts，an emergency order is implemented to cover the shortage of regular order and reduce equipment downtime in case of stock-outs. A cooperative-ordering model，which takes compound fill rate as the constraints and expected cost per unit time as objective function，is established to solve the joint optimization problem for multi-location order policy in the two supply modes.A heuristic algorithm is developed to optimize the proposed model on basis of Lagrangian factor and policy-iteration algorithm.The Monte-Carlo simulation model is presented to prescribe the demand and order behaviors.The analytical model is compared with genetic-algorithmoptimized simulation model in a set of designed experiments.The results show the analytical model derives near-optimal solution and operates with high efficiency.

operations research；spare parts；cooperative order；inventory；optimization

TP391

A

1000-1093（2015）02-0337-08

10.3969/j.issn.1000-1093.2015.02.022

2014-06-04

总装备部预先研究基金项目（51304010206、51327020105）

王慎（1983—），男，博士研究生。E-mail：wangshen_hust@163.com；李庆民（1957—），男，教授，博士生导师。E-mail：licheng0001@hotmail.com