正态应力-正态强度下可靠度精确置信下限

荣吉利，宋乾强，杨国孝，张涛

（1.北京理工大学宇航学院，北京100081；2.北京理工大学数学学院，北京100081；3.北京宇航系统工程研究所，北京100076）

正态应力-正态强度下可靠度精确置信下限

荣吉利1，宋乾强1，杨国孝2，张涛3

（1.北京理工大学宇航学院，北京100081；2.北京理工大学数学学院，北京100081；3.北京宇航系统工程研究所，北京100076）

针对应力和强度均服从正态分布，且二者的分布参数均未知的情况，有些学者给出了此条件下可靠度的近似置信下限，但是可靠度的近似置信下限在小样本情况下误差较大。基于应力-强度模型，结合相关统计学知识，给出可靠度的精确置信下限，同时与3种近似限方法进行了对比。结果表明：无论样本量大或者小，文中方法计算出的精度均高于3种近似限方法。当样本量较小时，推荐使用文中所给方法；当样本量较大时，可采用3种近似限方法进行近似计算。文中提出的方法可为可靠性评估提供一种新的途径。

应用统计数学；正态分布；可靠性；置信下限；精确限

0　引言

针对产品特性值服从正态分布，且总体均值和总体方差都未知的情况，当已知特性值上（下）规范限时，我国于1985年制定了GB 4885—85《正态分布完全样本可靠度单侧置信下限》，随后在此基础上进行了完善，于2009年制定了GB/T 4885—2009［1］。此方法基于一个特性值服从正态分布，另一个特性值为定值。然而，在实际工程中，如果产品特性值的规范限不是一个单一值，其值在一个范围内发生变化的话，则该方法将不再适用［2］。此时，可根据特性值变化的规律对其分布进行假设，最常见的模式就是考虑两个特性值均服从正态分布，即研究正态应力和正态强度模式下产品的可靠性。

当产品的应力和强度均服从正态分布，且其分布参数未知时，如果获得了应力和强度的完全样本，在此条件下如何计算此产品的可靠性？许多学者对这个问题进行了研究。已发表的文献大致可分为两类：一是讨论此模型下的近似限，文献［3-4］用泰勒级数展开的方法对可靠度置信下限进行了研究，文献［5］从假设检验原理角度进行分析。近似限在样本量较大时其误差可以接受，但是在小样本的情况下其误差较大；二是讨论此模型下的精确限，孙祝岭［6］提出了一种用正态分布变异系数的区间估计结果来处理此模式结构可靠度的经典精确置信下限的新方法，但是使用此方法时划分样本应遵循随机原则，排除人为因素影响，当测量结果排列顺序不一样时，可能导致计算的可靠度置信下限值有较大差别。除此之外，叶喜涛［7］也对此问题进行了研究，给出了这种情况下可靠度R的Bayes精确区间估计。到目前为止，基于正态应力和正态强度模式下产品可靠度的精确置信下限问题还没有得到很好的解决，仍然需要进一步的研究。

本文基于统计学原理，给出了此种模式下可靠度的精确置信下限，并与文献［3-5］中的3种方法进行对比。结果显示：本方法无论在样本量较小或者较大时，计算出的精度均高于文献［3-5］中的3种方法。当样本量较小时，推荐使用本文所给方法；当样本量较大时，可采用文献［3-5］中的3种方法进行近似计算。

1　可靠度精确置信下限

应力-强度模型广泛地应用于可靠性评估、可靠性设计中，其基本原理是将引起产品失效和阻止产品失效的因素分别看做应力M和强度L，当产品的L大于M时产品可靠。当L和M服从正态分布且相互独立时，产品的可靠度可以用（1）式计算：

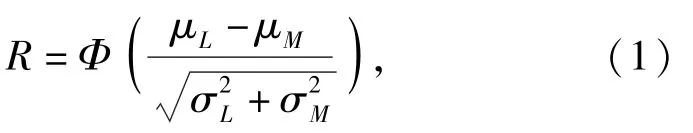
式中：μL和σL分别是强度L的均值和标准差；μM和 σM分别是应力M的均值和标准差；Φ为标准正态分布的分布函数。在用（1）式计算可靠度时，其均值和方差往往无法获取，如果采用样本均值和样本方差进行近似计算，一般需要较大的样本。对于小样本情况，尤其是某些航天产品可能只有几个试验样本，这样估计的结果并不可信。本文针对此问题，研究应力和强度均服从正态分布，且分布参数均未知时，其可靠度的精确置信下限问题。近似限方法是采用泰勒级数展开或者用样本均值、方差代替总体均值、方差等近似的方法进行求解，本文中精确限方法则没有进行相关的近似处理。

图1为可靠性分析中常用的应力-强度模型，f（x）和f（y）分别为强度和应力的概率密度曲线，阴影部分为“干涉区”，在此区域内可能发生失效。在进行推导之前，先引入以下两个引理：

引理1［8］设X1，X2，…，Xn是总体N（μ，σ2）的样本，S2是样本方差，则有

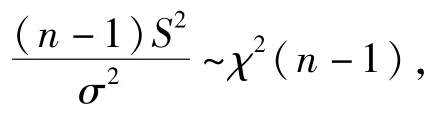
引理2［9］若随机变量U～N（0，1），V～χ2（m），且相互独立，则

服从自由度为m，非中心参数为δ的非中心t分布。

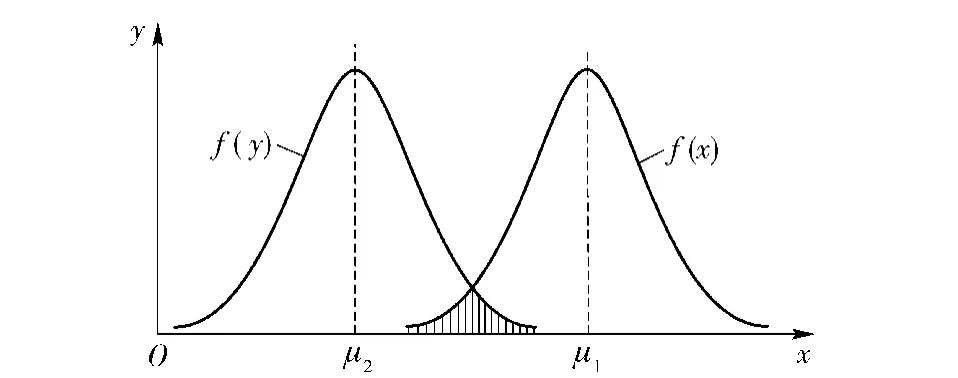
图1　可靠性评估模型Fig.1 Reliability evaluation model

设随机变量X1～N（μ1，σ21），X2～N（μ2，σ22），X1与X2相互独立，且其分布参数均未知。x1，x2，…，xe为 X1的e个样本，其样本均值和标准差分别为y1，y2，…，yf为X2的f个样本，其样本均值和标准差分别为

令随机变量W=X1-X2，则有设，则.和Sw分别为W的样本均值和样本标准差。因为X1与X2相互独立，故和Sw的值可分

别通过下式计算：

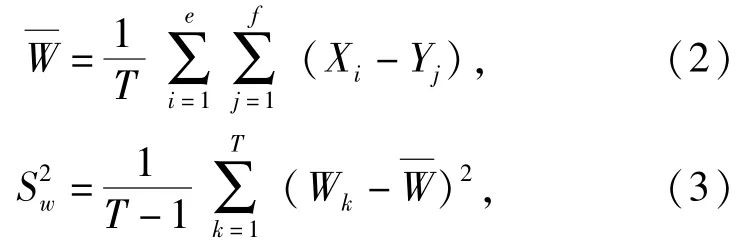
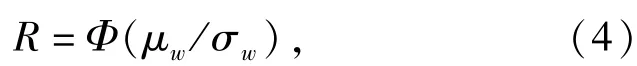
根据文献［10］所述，可将（4）式中均值和标准差看做由随机样本确定的随机变量。因此，可将R看成随机变量。

可靠度R的置信下限RL为

式中：URL为RL对应的标准正态分布的区间点。

在给定置信度γ下可靠度R的置信下限RL通过下式计算：

将（4）式、（5）式代入（6）式中可得

因为标准正态分布的分布函数Φ在（-∞，+∞）上为单调递增函数，故（7）式等价于

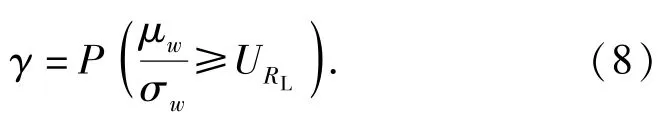
对（8）式进行恒等变形，可得

当给定置信水平γ时，根据试验的样本信息，对（10）式进行求解，解出URL，然后代入（5）式即可求得产品的可靠度置信下限。

2　近似限

针对第1节提出的问题，很多学者对其近似限进行了研究，为了与本文提出的方法进行对比，下面简单介绍其可靠度置信下限的计算公式，详细推导过程可参阅相关文献。本节中所涉及参数的具体定义可参阅相关对应文献。

周源泉在文献［3］中给出了可靠度置信下限的经典1阶近似限的计算公式：

此方法将样本均值和样本方差看做变量，在总体均值和总体方差处采用泰勒展开进行研究，得到了可靠度置信下限的1阶和2阶近似限。

Dimitri等在文献［4］中给出了可靠度置信下限的如下计算公式：

此方法实际上是周源泉在文献［3］中给出的可靠度置信下限的2阶近似限。不过，Dimitri等［4］针对更为一般的情况进行了研究，考虑了多维随机变量的情况，在此不再赘述。

Guo等于2004年在文献［5］中给出了如下计算公式：

Guo等［5］的研究工作从假设检验原理出发，在总体应力方差和强度方差之比已知和未知时进行分析，并与其他方法进行了对比，最后给出了可靠度置信下限的近似限。

3　3种方法的对比

下面给出两个例子，将第2节中的3种方法与本文给出的方法进行对比以及进一步的分析。

3.1当样本量较小时

示例1［6］：设某构件的抗力Y1、荷载效应Y2均服从正态分布，Y1与Y2互相独立。对Y1、Y2分别进行抽样观察，获得2组数据如下：9.10 N，6.17 N，10.73 N，13.83 N，13.60 N，15.20 N，3.45 N，9.30 N，13.29 N，6.74 N；3.31 N，2.31 N，2.15 N，3.02 N，3.23 N，1.88 N，3.43 N，3.60 N，4.13 N，3.63 N，3.67 N，3.63 N.求该结构可靠度R的置信度为0.90的置信下限。

变量W=Y1-Y2的样本量，样本均值以及样本标准差分别为：T=120，，Sw=3.754.表1为不同样本量下采用4种不同方法计算所得的可靠度置信下限值（计算中保持以上样本均值和样本标准差不变，只改变样本量的大小）。

表1中，在样本量为2×4时，RL2值很小，记为0.纵向对比RL～RL34列，可以看出：可靠度置信下限的值随着样本量的增加而增加。对于RL，样本量的增加导致试验中所包含的信息量变大，因而可靠度置信下限提高。对于RL1～RL33种近似限方法，其计算公式中忽略了泰勒展开中的高阶项，样本量越大，其计算结果越趋近于真实值，故可靠度置信下限变大。横向对比RL～RL3，可以看出：在样本量较小时，3种近似限方法计算出的可靠度置信下限值相互间相差较大，其中RL1最大，RL3次之，RL2最小。与本文所给方法对比可知，此3种方法计算的值相对较为保守，在小样本的情况下本方法具有明显的优势。

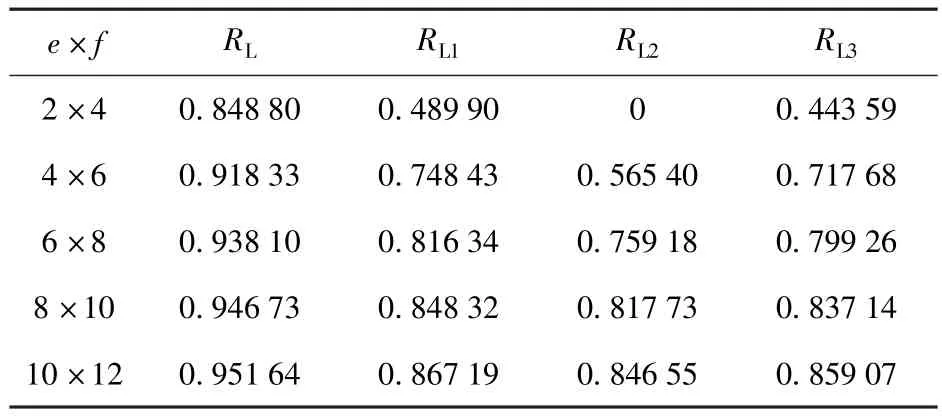
表1　不同样本量下的可靠度置信下限Tab.1 The lower confidence limit of reliability under diferent sample sizes

3.2当样本量较大时

示例2：随机变量X1、X2均服从正态分布，其分布参数未知，且相互独立。给出如表2所示的随机样本，其样本量分别为：e=40，f=50.当置信度为0.90时，对比4种方法。

表2　随机变量X1、X2的样本值Tab.2 The sample values of the random variable X and Y

当样本量为10×20时，分别选取表2中X1、X2的前10个和前20个数据作为此种情况下的样本，其他情况以此类推。3种近似限方法与本文所给方法之间的相对误差，如表3所示。

表3　不同样本量下4种方法之间的误差Tab.3 The error among 4 methods under different sample sizes%

从表3中可以看出：随着样本量的不断增加，此3种方法与本文所给方法之间的相对误差逐渐减小，当样本量为40×50时，3种近似限与精确限之间相对误差最大的仅为0.04%.故当样本量较大时，精确限与近似限之间相对误差较小，可用近似限进行粗略计算。

从示例1和示例2中可以看出，采用本文所给公式计算可靠度置信下限时，无论样本量是大或者小，其精度均高于本文所介绍的3种方法，其原因在于：本文给出的是可靠度的精确置信下限，其他3种方法给出的均是近似限，近似限方法在进行计算时忽略了高阶项，可能导致计算结果较为保守。且本文采用的方法包含了随机变量X1、X2更多的试验信息量。一般来说，当样本量较小时，推荐采用本文所给方法进行计算；当样本量较大时，可用文献［3-5］中的近似限方法进行近似求解。

4　结论

本文给出了应力和强度均服从正态分布，且其分布参数均未知时其结构可靠度的精确置信下限。通过与已有的3种近似限方法进行对比，证明了无论在样本量大或者是小时，此方法计算出的精度均高于此3种方法，尤其是在样本量较小时，推荐使用本文所给方法。本文所提出的方法可为可靠度置信下限的计算提供一种新的思路。

（

）

［1］全国统计方法应用标准化技术委员会.GB/T 4885—2009正态分布完全样本可靠度置信下限［S］.北京：中国标准出版社，2009. National Committee of Statistical Method Application and Standardization Technique.GB/T 4885—2009 Lower confidence limit of reliability for complete sample from normal distribution［S］.Beijing：Standards Press of China，2009.（in Chinese）

［2］荣吉利，张涛，徐天福，等.性能参数型航天器机构的可靠性试验评定方法［J］.宇航学报，2012，33（3）：387-391. RONG Ji-li，ZHANG Tao，XU Tian-fu，et al.Study on test method of reliability assessment used for performance parameter-measured spacecraft mechanism［J］.Journal of Astronautics，2012，33（3）：387-391.（in Chinese）

［3］周源泉.结构可靠性的经典近似限［J］.强度与环境，1986，13（5）：1-9. ZHOU Yuan-quan.Classical approximate limits for structural reliability［J］.Journal of Structure&Environment Engineering，1986，34（5）：1-9.（in Chinese）

［4］Dimitri B K，Wang W D，On the lower confidence limit of the calculated reliability for mechanical components and structural members.［C］∥The 38th AIAA/ASME/ASCE/AHS/ASC Structures，Structural Dynamics，and Matericals Conference and Exhibit.US：AIAA，1997.

［5］Guo H Z，Krishnamoorthy K.New approximate inferential methods for the reliability parameter in a stress-strength model：the normal case［J］.Communications In Statistics：Theory and Methods，2004，33（7）：1715-1731.

［6］孙祝岭.正态应力和正态强度可靠性的经典精确限［J］.兵工学报，2011，32（3）：354-358. SUN Zhu-ling.Classical exact limits of structural reliability for normal stress and normal strength［J］.Acta Armamentarii，2011，32（3）：354-358.（in Chinese）

［7］叶喜涛.正态应力强度结构可靠性的精确限［J］.系统工程与电子技术，1997，19（9）：77-81. YE Xi-tao.The exact limits of structural reliability for normal stress and normal strength［J］.Systems Engineering and Electronics，1997，19（9）：77-81.（in Chinese）

［8］盛骤，谢世千，潘承毅.概率论与数量统计［M］.北京：高等教育出版社，2004. SHENG Zhou，XIE Shi-qian，PAN Cheng-yi.Probability and mathematical statistics［M］.Beijing：Higher Education Press，2004.（in Chinese）

［9］韦博成.参数统计教程［M］.北京：高等教育出版社，2006. WEI Bo-cheng.A course in parametric statistics［M］.Beijing：Higher Education Press，2006.（in Chinese）

［10］周源泉，翁朝曦.可靠性评定［M］.北京：科学出版社，1990. ZHOU Yuan-quan，WENGChao-xi.Reliabilityassessment［M］.Beijing：Science Press，1990.（in Chinese）

The Exact Lower Confidence Limit of Reliability for Normal Stress and Normal Strength

RONG Ji-li1，SONG Qian-qiang1，YANG Guo-xiao2，ZHANG Tao3
（1.School of Aerospace Engineering，Beijing Institute of Technology，Beijing 100081，China；2.School of Mathematics，Beijing Institute of Technology，Beijing 100081，China；3.Beijing Institute of Space System Engineering，Beijing 100076，China）

For stress and strength obey normal distribution and their distributed parameters are unknown，some researchers have given approximate lower confidence limits of its reliability under these conditions. But the error of approximately confidence limits is large in the case of small samples.Based on stressstrength model and relevant statistical knowledge，the exact lower confidence limit of its reliability is presented.The proposed method is compared with three kinds of approximate limits methods.The result shows that no matter large or small the size of the sample is，the accuracy of the method mentioned in this paper is higher than those other three methods.When the size of the sample is small，it is recommended to use this proposed method；when the size of the sample is large，these three methods can be used for approximate calculation.This proposed method provides a new approach for the assessment of the reliability.

applied statistical mathematics；normal distribution；reliability；lower confidence limit；exact limits

TB114.3

A

1000-1093（2015）02-0332-05

10.3969/j.issn.1000-1093.2015.02.021

2014-05-18

国家部委预先研究项目（C4220062206）

荣吉利（1964—），男，教授，博士生导师。E-mail：rongjili@bit.edu.cn