基于混沌神经网络的防空火箭炮交流伺服系统状态预测研究

胡健，马大为，姚建勇，刘龙

（南京理工大学机械工程学院，江苏南京210094）

基于混沌神经网络的防空火箭炮交流伺服系统状态预测研究

胡健，马大为，姚建勇，刘龙

（南京理工大学机械工程学院，江苏南京210094）

为了更加准确地对系统非线性非平稳状态趋势进行预测，运用基于神经网络的混沌预测方法对防空火箭炮交流伺服系统的速度量进行了预测，为基于速度预测值的系统非线性非平稳状态趋势预测奠定了基础。利用C-C法选择了合适的嵌入维和时间延迟，对防空火箭炮交流伺服系统不规则运动的实验数据进行了相空间重构并进行了分析。在原Elman网络中增加了输出层关联单元，并把自反馈增益系数当作连接权值投入到网络的训练中，以增强Elman网络非线性逼近能力，在此基础上建立了基于改进型Elman网络的混沌预测模型。采用基于最大Lyapunov指数预测法和混沌神经网络预测法对系统状态进行了预测，两种方法的预测结果表明，后一种方法对防空火箭炮交流伺服系统速度值预测精度更高，从而使得基于此的系统非线性非平稳状态趋势预测更有效。

兵器科学与技术；火箭炮；交流伺服系统；状态预测；相空间重构；混沌神经网络

0　引言

防空火箭炮交流伺服系统由永磁同步电机、驱动器、减速器及相应的负载组成，是一种典型的电机传动系统，同时也是一种典型多变量强耦合的非线性系统。其不规则运动的存在由来已久，主要表现为转矩、转速的间歇振荡、控制性能的不稳定、系统不规则电磁噪声等［1］，它们的出现直接影响系统的总体性能和可靠性。长期以来，由于交流传动系统的复杂性，人们往往把这些不规则运动的产生归结为外界随机干扰或系统故障，并用传统的平稳信号分析方法去分析，以期解决问题。这种认识上的局限性束缚了人们解决问题的思路。目前已有部分研究表明，在某些参数工作条件下，类似防空火箭炮交流伺服系统的机电传动系统会出现混沌运动［1-3］，其动力学特性往往表现出复杂性和非线性。此时，传统的平稳信号分析方法不再适用，若对这些非线性问题进行线性化处理，系统的输出将远离事实本相。因此，运用非线性动力学从混沌的角度分析防空火箭炮交流伺服系统的不规则运动并进行状态预测与故障诊断有十分重要的意义。

非线性系统的混沌预测方法分为两大类：一是基于非线性数学模型的动力学方法，二是基于实际观测数据的相空间重构法。前者根据实际问题建立描述系统的动态数学模型，然后求解这个数学模型，最后反过来根据计算结果进行预测。但由于非线性系统本身的复杂性，在建立数学模型的过程中，需要事先做出一定的假设和近似处理，这就使得建立的数学模型并不那么精确，从而使得基于该模型的混沌预测效果不是很理想。而用相空间重构法进行预测时，在预测之前不用做任何假设与数据处理，而是直接利用采集的非线性系统时间序列进行分析，得到时间序列几何不变量进行预测，这样减少了预测的主观性，预测效果也更好。

常见的基于相空间重构的混沌时间序列预测方法有全局预测法［4］、局域预测法［5］以及基于最大Lyapunov指数的预测方法［6-7］。最近几年，神经网络因为其强大的非线性系统逼近拟合能力而被引入到非线性系统的混沌预测中来［8-10］，神经网络被用来构造一个非线性映射来近似地还原原系统，这一非线性映射即为要建立的预测模型。但这些混沌预测算法仍然存在不少的缺陷，如收敛速度慢，预测精度不高等。本文利用改进的Elman网络逼近嵌入空间中的相点演化规律，利用观测得到的时间序列历史数据建立时间序列的预测模型。结果表明，该方法对防空火箭炮交流伺服系统具有较好的非线性拟合能力和较高的预测精度。

1　防空火箭炮交流伺服系统实验现象

1.1防空火箭炮交流伺服系统的组成

防空多管火箭炮交流伺服系统由俯仰和方位两个轴上的交流伺服系统组成。每一个轴上的交流伺服系统主要由位置控制器、伺服驱动器、永磁同步电机、减速器、机械机构、旋转变压器以及电源组成。具有接受指挥系统的目标指示、进行俯仰和方位自动调炮以及目标跟踪的功能。具体的工作原理如下：炮位计算机通过串口将目标未来点位置发送给位置控制器，位置控制器通过其上的轴角转换电路采集旋转变压器送来的当前位置，经过控制律计算出控制量，通过D/A转换控制驱动器带动相应的伺服电机运转，再经过减速器带动相应的机械机构运动，从而实现高精度调炮和跟踪。其组成框图如图1所示，原理样机如图2所示。

图1　防空火箭炮交流伺服系统组成框图Fig.1 Block diagram of air-defense rocket launcher

1.2实验现象

由于方位轴和俯仰轴交流伺服系统的组成、结构是完全一样的，因此我们以其中一轴（俯仰轴）为例进行分析。通过改变驱动器的控制参数来改变闭环系统的动态特性。大量实验发现，随着控制参数的改变，防空火箭炮交流伺服系统先后出现3种典型运动状态：1）转速平稳无波动，如图3（a）所示；2）转速呈周期性波动，周期性波动呈近似正弦波形，具有固定周期，如图3（b）所示；3）转速含有不规则波动，其没有明显的波动周期，是一种较为复杂的不稳定性现象，如图3（c）所示。目前还没有相关研究成果能够精确预测第3种不规则运动，本文利用基于改进Elman网络的混沌时间序列预测方法预测这种不规则运动。

图2　防空火箭炮交流伺服系统原理样机Fig.2 Prototype of air-defense rocket launcher

图3　防空火箭炮交流伺服系统不同参数下转速曲线Fig.3 Velocity curves under different parameters

2　防空火箭炮交流伺服系统混沌预测算法

2.1相空间重构

为了有效恢复高维复杂动力学系统的混沌动力学特性，相空间重构理论被提出。其基本思想是：系统中任一分量的演化都是由与之相互作用的其他分量所决定的，因此这些相关分量的信息就隐藏在任一分量的发展过程中。为了重构一个等价的状态空间，只需考察一个分量，并将它在某些固定的时间延迟点上的测量作为新维处理，即延迟值被看成是新的坐标，它们确定了某个多维状态空间中的一点。重复这一过程并测量相对于不同时间的各延迟量就可以产生出许多这样的点，该方法可以将吸引子的许多性质保存下来，即用系统的一个观察量可以重构出原动力系统模型，初步确定系统真实相空间的维数［11］。

设时间序列为x（t），t=1，2，…，N，嵌入维数为m，时间延迟为τ，则重构相空间为

式中：X（ti）为m维相空间中的相点；M为相点个数；集合｛X（ti）|i=1，2，…，M｝描述了系统在相空间中的演化轨迹。根据Takens定理，只要m、τ选择合理，重构相空间与原系统是拓扑等价的。因此存在一个光滑映射f∶Rm→Rm给出相空间轨迹的表达式为

上述映射可表示成时间序列为

根据此方法，我们只需采集防空火箭炮交流伺服系统的一个状态变量（如电流、速度或位置），通过相空间重构即可恢复原系统非线性动力学特性，从而进行状态预测。在众多状态变量中，角速度可以更加直观地反映系统运动特性且较易测得，因此本文在防空火箭炮交流伺服系统所获得的最优控制算法的控制下，采集系统角速度输出构成一维时间序列，采样时间间隔为20 ms，共采集3 000个点，利用此一维时间序列进行相空间重构。

2.2嵌入维和时间延迟的选取

在重构相空间中，时间延迟τ和嵌入维数m的选取具有十分重要的意义，同时这种选取也是很困难的。由于实际时间序列存在噪声干扰，如果τ太小，相空间轨迹会向同一位置挤压，信息不易显露，产生冗余误差；如果τ太大，会导致某一时刻和后一时刻的动力学特性变化剧烈，使得简单的几何对象变得很复杂，动力系统信号失真，产生不相关误差。

目前常用的τ估计方法有自相关函数法和互信息法，前者适用于小数据组，计算方便，但不适合非线性问题，后者适用于大数据组，适合非线性问题，但计算不方便。Kim等提出一种改进方法，称为C-C方法，该方法应用关联积分能够同时估计出m和τ，容易操作，计算量小，效果好，而且具有较强的抗噪声能力（30%以下）［10］。本文采用C-C法选取时间延迟τ和嵌入维数m，具体步骤如下：

在此基础上，对3组实验数据进行相空间重构，来观察一下实验数据有何特点。

图5为转速相空间重构的相轨迹，转速相空间重构的相轨迹与系统相空间的相轨迹在表现系统的动力学本质特性上是等价的。图5（a）表明系统在做周期2运动，图5（b）表明系统在做拟周期运动，图5（c）表明系统进入混沌状态，在做混沌运动。从中可以看出随着系统参数的变化，系统从平稳运动状态进入周期运动状态，直至进入混沌运动状态。

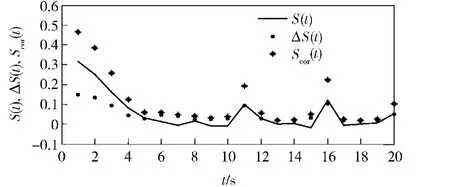
图4　随t的变化曲线Fig.4 Curves of

2.3基于混沌神经网络的状态预测

选择好合适的嵌入维和时间延迟，重构好相空间，就可以用混沌预测的方法预测系统状态。混沌预测方法就是在相空间中找到一个非线性模型，去逼近系统动态特性，即前面所说的光滑映射f∶Rm→Rm，实现一定时间内的预测，同时该模型也可用来识别系统是否包含混沌特性［10］。神经网络是非线性系统逼近和建模的有效工具，在混沌时间序列的重构相空间中，可以利用神经网络逼近相点的演化规律，利用观测得到的时间序列历史数据建立时间序列的预测模型。基于混沌神经网络的预测原理图如图6所示。

采用神经网络进行序列建模和预测时，首先要考虑网络结构的设计问题。神经网络的拓扑结构不仅影响到网络的泛化能力，同时也影响网络的学习速度。文献［8-9］分别探讨了径向基函数（RBF）神经网络、反向传播（BP）神经网络的混沌时间序列预测问题。这些算法比较复杂，运行的时间较长，且预测精度不高，收敛速度慢。从（1）式可以看出系统某一瞬时状态可由m维的延迟坐标向量确定，因此在网络结构中应该包含延时单元，以反映延迟坐标向量对系统状态的影响。而RBF神经网络、BP神经网络均不包含这样的单元，因此不能较好地反映系统的动态特性。最近提出的一种Elman神经网络［11］在前馈网络的隐含层中增加一个承接层，作为一步延时算子，达到记忆的目的，从而具有适应时变特性的能力，能直接反映动态系统的特性。因此，本文利用Elman网络进行系统混沌预测。

为了增加神经元对历史数据的敏感程度，本文在原Elman网络中增加了输出层关联单元，以存储输出层的历史数据，并反馈给输出单元。此外，标准Elman网络中自反馈增益α是固定值，一般是根据经验来选取，α值选择得不好会导致系统出现发散现象。本文考虑把各个α当作连接权值投入到网络的训练中，从而实现自反馈增益系数的动态修正。由此设计了一个适于本系统混沌预测的改进型Elman网络，其结构如图7所示。Elman神经网络采用经典的梯度下降法进行在线训练学习，权值初值可选一个随机值，经过梯度下降法训练后会收敛到一个稳态值［12］。改进后的Elman网络具有较高的收敛精度和较短的学习时间。由于系统速度量经过相空间重构后的相点运动轨迹可以反映出系统的动力学特性，所以混沌神经网络的输入量选为系统相空间中的相点ω（ti），ω（ti+τ），ω（ti+2τ），因此输入层有3个节点。由于进行的是单步预测，输出量为下一时刻的速度量ω（ti+3τ），所以输出层和输出层关联单元只有1个节点，隐层和隐层关联单元节点数的选择至关重要，多了则增加计算量影响预测速度，少了则影响存储记忆能力导致预测精度降低，综合考虑这两个因素根据经验选为4个节点，则网络的状态空间表达式如图7所示。

图5　防空火箭炮系统相空间重构的相轨迹Fig.5 Phase orbit of air defense rocket launcher

图6　混沌神经网络预测原理图Fig.6 Schematic diagram of chaotic neural network

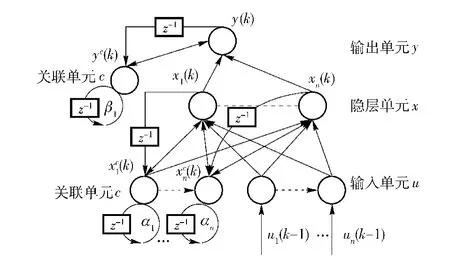
图7　改进型Elman网络Fig.7 Improved Elman network

图7中：u1（k-1），…，un（k-1）为输入量；

（4）式～（7）式中：Wxc、Wxu、Wyx、Wyc分别为隐层关联单元到隐层，输入单元到隐层，隐层到输出单元及输出层关联单元到输出单元的权矩阵；Wα=diag［α1，…，αn］，Wγ=diag［γ1，…，γn］，为自反馈增益矩阵；阈值函数f选为Sigmoid函数，即f=1/（1+ e-x）；x（k）=［x1（k），x2（k），…，xn（k）］；xc（k）=［xc1（k），xc2（k），…，xcn（k）］.

设第k步系统的实际输出为yr（k），定义误差函数为，将E对连接权值及矩阵γ1、Wyx、Wyc、Wα、Wxu、Wxc分别求偏导，由梯度下降法可得Elman网络的学习算法为

3　预测分析

混沌预测神经网络结构和训练算法建立之后，就可以开始对混沌神经网络进行训练，即进入学习阶段。采集防空火箭炮交流伺服系统的速度数据，输入网络输入层，得到输出结果，然后与实际数据进行比较，如果存在误差，立即进行反向传播过程，并修正网络权值以减小误差。正向输出计算和反向权值修改交替进行。

经过反复的训练，网络的权值已经达到了预测的要求，然后将此混沌神经网络应用到防空火箭炮交流伺服系统状态预测中，对经过降噪的数据进行后期趋势预测。为了比较方法的优越性，将基于Elman网络的混沌神经网络预测法与基于最大Lyapunov指数的预测方法进行比较，采集的数据是系统处于混沌运动状态时的速度值，结果如图8和表1所示。通过与基于最大Lyapunov指数的预测方法进行比较可以看出，混沌神经网络预测法的预测精度比较高，预测效果更理想。同时可以看出，由于混沌系统的耗散性和对初值的极端敏感性，在短期内预测精度很高，但长时间预测误差急剧增大，说明混沌动力系统只能作短期预测。需要说明的是，不同的神经网络权值初值的选取有可能导致系统陷入局部最小点，从而导致预测精度的降低。为了避免出现这种情况，可以在梯度更新法中增加一个冲量项以带动梯度下降过程，冲过狭窄的局部最小值而到达全局最小值。

图8　混沌神经网络预测法与基于最大Lyapunov指数预测法对比图Fig.8 Comparison of two methods

表1　混沌神经网络预测法与基于最大Lyapunov指数预测法比较Tab.1 Comparison table of two methods

在精确预测系统速度值的基础上，可以直接观察已经测得的角速度和预测的角速度序列的时序图或相空间重构后的相图判断系统的当前状态，如图3、图5所示。也可以利用已经测得的角速度和预测的角速度序列根据最小数据量法［13］计算出系统最大Lyapunov指数，从而准确判断系统是否进入非线性非平稳状态（即混沌状态）。

4　结论

基于混沌神经网络的预测是通过基于数据序列客观存在的内在混沌特性实现的，神经网络的预测模型输入端完全由混沌特征决定，这样避免了以往预测方法中主观确定因素的影响。通过与基于最大Lyapunov指数的预测法进行比较可以看出，混沌神经网络预测法的预测精度比较高，预测效果较理想。在此基础上，可以更加准确地对系统非线性非平稳状态进行趋势预测。

（

）

［1］张波，李忠，毛宗源，等.电机传动系统的不规则运动和混沌现象初探［J］.中国电机工程学报，2001，21（7）：40-45. ZHANG Bo，LI Zhong，MAO Zong-yuan，et al.A primary study on an erratic behavior and chaotic phenomena of electric machine drive systems［J］.Proceedings of the CSEE，2001，21（7）：40-45.（in Chinese）

［2］Li Z，Paris J B，Joo Y H，et al.Bifurcations and chaos in a permanent-magnet synchronous motor［J］.IEEE Transactions on Circuits and Systems-I：Fundamental Theory and Applications，2002，49（3）：383-387.

［3］Jing Z，Yu C，Chen G.Complex dynamics in a permanent-magnet synchronous motor model［J］.Chaos，Solitons and Fractals，2004，22（4）：831-848.

［4］张森，肖先赐.混沌时间序列全局预测新方法-连分式法［J］.物理学报，2005，54（11）：5062-5068. ZHANG Sen，XIAO Xian-ci.A new method of global prediction for chaotic time series based on continued fractions［J］.Acta Physica Sinica，2005，54（11）：5062-5068.（in Chinese）

［5］郭创新，王扬，沈勇，等.风电场短期风速的多变量局域预测法［J］.中国电机工程学报，2012，32（1）：24-31. GUO Chuang-xin，WANG Yang，SHEN Yong，et al.Multivariate local prediction method for short-term wind speed of wind farm［J］. Proceedings of the CSEE，2012，32（1）：24-31.（in Chinese）

［6］张勇，关伟.基于最大Lyapunov指数的多变量混沌时间序列预测［J］.物理学报，2009，58（2）：756-762. ZHANG Yong，GUAN Wei.Predication of multivariable chaotic time series based on maximal Lyapunov exponent［J］.Acta Physica Sinica，2009，58（2）：756-762.（in Chinese）

［7］张文超，谭思超，高璞珍.基于Lyapunov指数的摇摆条件下自然循环流动不稳定性混沌预测［J］.物理学报，2013，62（6）：060502. ZHANG Wen-chao，TAN Si-chao，GAO Pu-zhen.Chaotic forecasting of natural circulation flow instabilities under rolling motion based on Lyapunov exponents［J］.Acta Physica Sinica，2013，62（6）：060502.（in Chinese）

［8］冯兴杰，潘文欣，卢楠.基于小波包的RBF神经网络网络流量混沌预测［J］.计算机工程与设计，2012，33（5）：1681-1686. FENG Xing-jie，PAN Wen-xin，LU Nan.Research on chaotic prediction method of network traffic based on wavelet packet［J］. Computer Engineering and Design，2012，33（5）：1681-1686.（in Chinese）

［9］朱春梅，徐小力，张建民.基于混沌神经网络理论的机电设备状态趋势预测研究［J］.北京理工大学学报，2009，29（6）：506-509. ZHU Chun-mei，XU Xiao-li，ZHANG Jian-min.Electromechanical equipment fault forecasting research based on chaos-neural networks theory［J］.Transactions of Beijing Institute of Technology，2009，29（6）：506-509.（in Chinese）

［10］吕金虎，陆君安，陈士华.混沌时间序列分析及其应用［M］.武汉：武汉大学出版社，2001. LYU Jin-hu，LU Jun-an，CHEN Shi-hua.Chaotic time sequence analysis and its application［M］.Wuhan：Publishing House of Wuhan University，2001.（in Chinese）

［11］HE Hai-tao，TIAN Xia.An improved Elman network and its application in flatness prediction modeling［C］∥Second International Conference on Innovative Computing，Information and Control.Piscataway，NJ，US：IEEE Computer Society，2008：44-48.

［12］WU Wei，FENG Guo-rui，LI Zheng-xue，et al.Deterministic convergence of an online gradient method for BP neural networks［J］. IEEE Transactions on Neural Networks，2005，16（3）：533-540.

［13］张海龙，闵富红，王恩荣.关于Lyapunov指数计算方法的比较［J］.南京师范大学学报，2012，12（1）：5-9. ZHANG Hai-long，MIN Fu-hong，WANG En-rong.The comparison for Lyapunov exponents calculation methods［J］.Journal of Nanjing Normal University，2012，12（1）：5-9.（in Chinese）

State Forecasting Research of Air-defense Rocket Launcher AC Servo System Based on Chaotic Neural Network

HU Jian，MA Da-wei，YAO Jian-yong，LIU Long
（School of Mechanical Engineering，Nanjing University of Science and Technology，Nanjing 210094，Jiangsu，China）

To predict the system nonlinear and non-stationary conditions more accurately，a method of chaos prediction based on chaotic neural networks is introduced to predict the velocity of the air-defense rocket launcher AC servo system，which paves the way for the trend prediction of system nonlinear and non-stationary conditions.C-C method is used to select the proper embedding dimension and time delay. The phase space of system is reconstituted using experimental data of system's irregular movement and is analyzed.The context neurons of output layer are added to the original Elman network，and the self-feedback gain coefficients are trained as connective weight，which could strengthen the nonlinear approximation ability of Elman network.Then a model of chaotic neural network based on the improved Elman network is set up.The predictions based on the maximun Lyapunov exponent and chaotic neural network are performed，respectively.The predicted results show that the prediction based on the chaotic neural network has a higher accuracy，which makes the trend forecasting of the system more effectively.

ordnance science and technology；rocket launcher；servo system；state forecasting；phasespace reconstruction；chaotic neural network

TJ713

A

1000-1093（2015）02-0220-07

10.3969/j.issn.1000-1093.2015.02.005

2014-04-23

国家自然科学基金项目（51305203）；“十二五”国防基础科研项目（B2620110005）；江苏省博士后基金项目（1302002A）

胡健（1980—），女，讲师，硕士生导师。E-mail：hujiannjust@163.com；马大为（1953—），男，教授，博士生导师。E-mail：ma_dawei@njust.edu.cn