相空间中Herglotz型微分变分原理与一类新型绝热不变量*

徐鑫鑫，张毅

(1. 苏州科技大学数理学院，江苏 苏州 215009;2. 苏州科技大学土木工程学院，江苏 苏州 215011)

动力学系统的对称性和守恒量具有重要的数学意义和物理意义，关于这方面的研究已经取得了许多重要的结果[1-4]。实际上绝热不变量和守恒量的关系是密不可分的，绝热不变量是一定条件下近似不变的量。1996年赵跃宇和梅凤翔在增广相空间中研究了完整和非完整力学系统的绝热不变量及其逆问题[5]，给出了力学系统的Noether型绝热不变量。此后，Noether型绝热不变量被推广到Birkhoff系统[6]、Lagrange系统[7]、准坐标下非完整系统[8]等。张毅给出了广义经典力学[9]、Birkhoff系统[10]的Hojman型绝热不变量。罗绍凯给出了Lutzky型绝热不变量[11]。丁宁等给出可控非完整系统Mei型绝热不变量[12]。最近，关于分数阶力学系统和非线性非保守系统的绝热不变量研究也取得了一些新进展[13-17]。

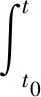
1 微分变分原理与精确不变量

相空间中Herglotz型微分变分原理为[21]:

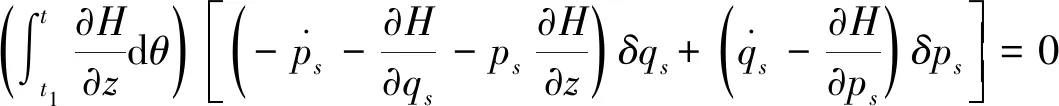
(1)

对于完整系统，δqs和δps互相独立，因此有

或

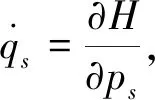
(3)

方程(3)是相空间中非保守系统基于Herglotz广义变分原理的Hamilton正则方程[21]。

引进时间t和广义坐标qs和广义动量ps的参数无穷小变换

t*=t+Δt,

(4)

或其展开式

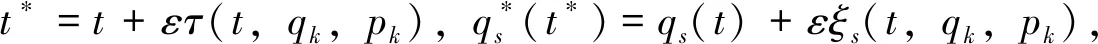
(5)

由等时变分和非等时变分之间的关系可得[21]

(6)

同理

(7)

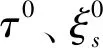
将式(6)，(7)代入原理(1)，整理得

(8)

由于

(9)

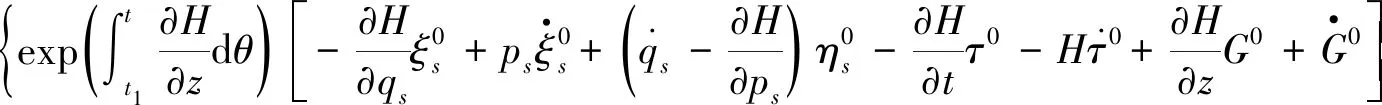
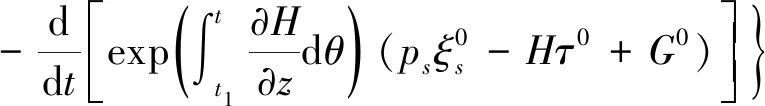
(10)

其中，G0=G0(t,qs,ps)称为规范函数。式(10)是相空间中非保守系统的Herglotz型微分变分原理不变性条件的变换。由式(10)，立即可得到

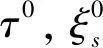
(11)

则系统存在守恒量

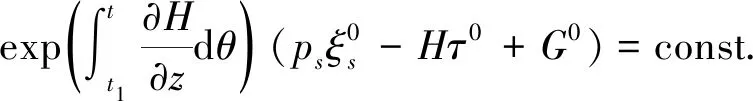
(12)

当G0≡0时，定理1给出文献[20]的结果。守恒量(12)是系统未受扰动时的不变量，因此它是一个精确不变量。

2 一类新型绝热不变量

如果Im(t,qs,ps,z,ε)是相空间中非保守系统的一个含有ε的最高次幂为m的物理量，它对时间t的一阶导数正比于εm+1，那么Im称为该系统的m阶绝热不变量。

假设相空间中非保守系统(2)受到了一个小扰动εQs的作用，则方程(2)成为

(13)

由于小扰动εQs的作用，该系统原有的对称性和不变量都会发生改变。假设受扰系统的无限小生成函数τ(t,qk,pk),ξs(t,qk,pk)及ηs(t,qk,pk)可表示为

τ=τ0+ετ1+ε2τ2+…，

(14)

并满足

(15)

其中，G为规范函数，记为

G=G0+εG1+ε2G2+…

(16)

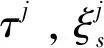
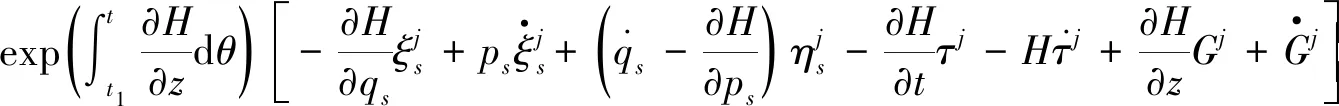
(17)

则

(18)

是该系统的一个m阶绝热不变量。

证明：由条件(17)和方程(13)，得

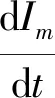
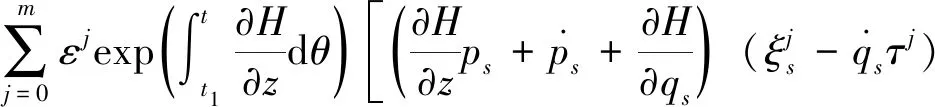
(19)

因此，Im是一个m阶绝热不变量。式(18)是我们基于Herglotz广义变分原理导出的一类新型绝热不变量。

3 逆问题

假设相空间中非保守系统(2)在小扰动εQs作用下存在如下一阶绝热不变量

I1=F0(t,qs,ps,z)+εF1(t,qs,ps,z)

(20)

因其轨道应满足Hamilton正则方程(13)，所以有

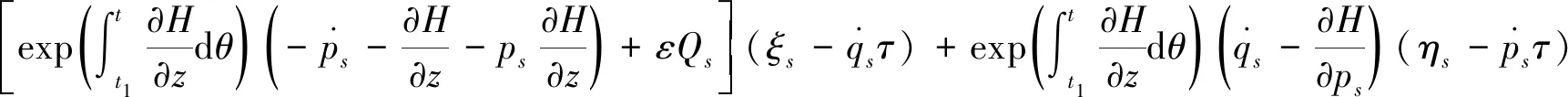
(21)

由于

根据(19)式，并综合(21),(22)两式则可得

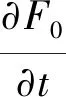
(23)

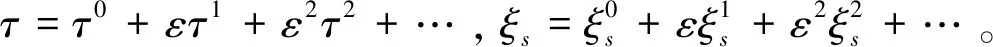
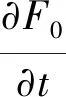
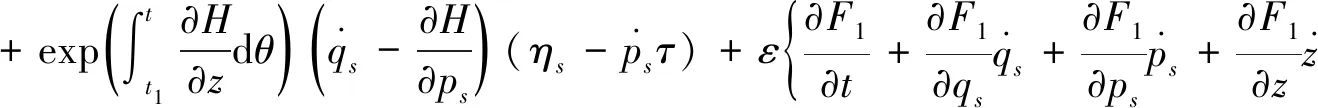
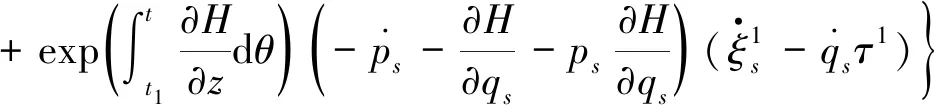
(24)

因此，若有

(25)

即

(26)

进一步假设

(27)

由(26)和(27)式可以解得无扰动部分对应的生成函数分别为

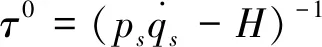
(28)

(29)

进一步地分析，可以得到小扰动作用下生成函数的摄动项的结果为

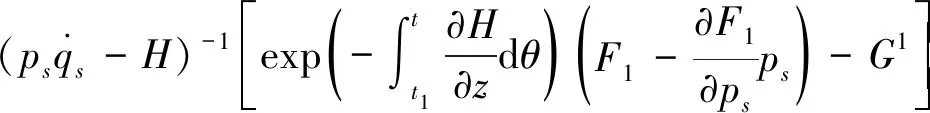
(30)

(31)

于是有

定理3 如果相空间中非保守系统(2)在小扰动εQs作用下存在一个一阶绝热不变量，形如(20)式，则存在相应的无穷小变换，无摄动项的生成函数为(28)和(29)，摄动项的生成函数为(30)和(31)。

如果令

(32)

(33)

无穷小变换(5)可写成

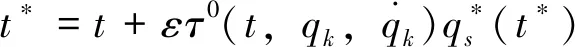
(34)

于是定理2和定理3给出位形空间中Herglotz变分问题的绝热不变量。我们有如下推论：

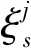
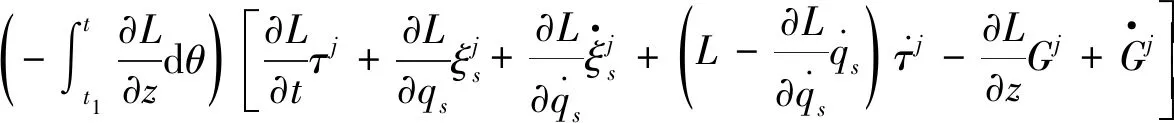
(35)

则

(36)

是该系统的一个m阶绝热不变量。

推论2 如果位形空间中非保守系统在小扰动εQs作用下存在一个一阶绝热不变量，形如

(37)

则存在相应的无穷小变换,得到无摄动项的生成函数为(38)和(39)和摄动项的生成函数为(40)和(41)。

(38)

(39)

(40)

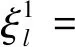
(41)

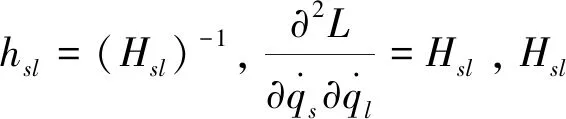
4 算 例

研究平方阻尼振子，其运动微分方程为[28]

(42)

Herglotz型Hamilton正则方程给出[21]

(43)

(44)

方程(44)有解

(45)

由定理1，该系统的一个精确不变量为

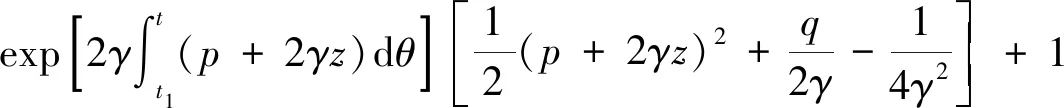
(46)

下面研究系统的绝热不变量。假设系统受到的小扰动为

(47)

方程(17)给出

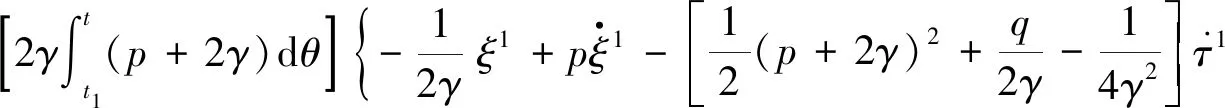
(48)

方程(48)有解

τ1=-1，ξ1=0，G1=1,η1=a

(49)

由定理2，则该系统有如下一阶绝热不变量

类似地，可求得系统的更高阶绝热不变量。

最后研究逆问题。假设系统受到小扰动(47)的作用，且存在一阶绝热不变量(50)，则由(26)和(27)式得到

(51)

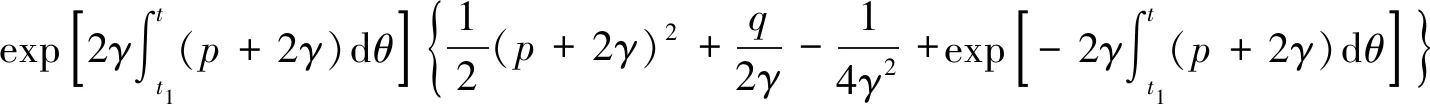
(52)

若取

(53)

则有

τ0=-1,ξ0=0

(54)

若取

G1=1

(55)

由式(30)和(31)可得到

τ1=-1，ξ1=0

(56)

因此，生成元(54)和(56)给出与一阶绝热不变量(50)相应的无穷小变换。

5 结 论

文章基于相空间中Herglotz型微分变分原理，导出了一类新型绝热不变量。主要工作包括：一是基于Herglotz型微分变分原理给出了相空间中非保守系统的精确不变量(12)及其存在条件(11)；二是给出了相空间中非保守系统的一类新型绝热不变量(18)，并加以证明；三是讨论了绝热不变量的逆问题。主要结果为三个定理及其两个推论。本文的方法和结果可进一步加以推广和应用，如基于Herglotz型微分变分原理构建Birkhoff系统或非完整系统的绝热不变量等。