Progress of the study on Landau-Ginzburg A-model

, ,

(1. School of Mathematical Sciences, Peking University, Beijing 100871, China;2. School of Mathematics (Zhuhai), Sun Yat-sen University, Zhuhai 519082, China;3. Humboldt-Universität zu Berlin, Berlin 12489, Germany)

Abstract：A brief introduction of Landau-Ginzburg A-model (LG A-model) in homological mirror symmetry is given. Firstly, a short review of the general picture of the homological mirror symmetry is given. Then the background of Landau-Ginzburg model and its role in homological mirror symmetry are discussed. Finally, a brief introduction of our recent work on the Fukaya category of LG model is included. Both mathematical and physical backgrounds are tried to include in this introduction as much as posible.

Key words：Fukaya category；Landau-Ginzburg model

In general, mirror symmetry describes a phenomenon, that the structures of two entirely different mathematical objects are equivalent (in a certain sense). In principle, these objects are two realizations of the same physical theory (often in string theory). In 1990s, Candelas, de la Ossa, Green and Parkes[1] found that we can count the number of algebraic curves via transformations of Picard-Fuchs equation, for quintics inP4. This conjectural result was proved by Givental [2-4] and Liu-Lian-Yau [5-8] respectively in a mathematically rigorous way, and by Hori-Vafa [9] using arguments in physics.

The aforementioned curve-counting version of mirror symmetry is about the closed string. Here the terminology ‘closed string’ means we consider one dimensional string without boundary, moving in certain dimensional physical world. In Hori-Vafa’s theory, the T-duality plays an important role, which relates strings of scalesRand 1/Rand gives a correspondence of invariants on them.

If we consider the string with boundary, there also should be some kind of mirror symmetry phenomenon. It is Kontsevich who proposed a conjecture on open string version in 1994. This program is nowadays known as homological mirror symmetry. Instead of numberical curve counting, the homological mirror symmetry is at the categorical level. For a pair of manifolds mirror to each other, the derived Fukaya category (A-model) of one should be equivalent to the the derived category of coherent sheaves (B-model) of the other, and vice versa.

Here we need some explaination of Fukaya categories, which are constructed from the Lagrangian Floer theory on symplectic manifolds. In general, the objects of the Fukaya category of a symplectic manifoldMare certain Lagrangian submanifolds. For a pair (L0,L1) of such objects, the morphism space Hom(L0,L1) between them are the module freely generated by their intersections, after intersections of Lagrangians are made transverse. We often useCF(L0,L1) to denote this Hom space.

Forpi∈Li-1∩Li,i=1,2,…,d, andp0∈L0∩Ld, we consider mapsufrom the unit disc toM, satisfying the Cauchy-Riemann equation

The disc here hasd+1 marked pointsz0,…,zdon the boundary, which divide the boundary circle intod+1 segments. Whenzapproaches some marked pointzi,the limit ofu(z) is required to bepi. Each boundary segments are required to be mapped to one of Lagragians, and the order of the Lagrangians is suitably chosen to make the conditions compatible. If certain tranversality condition is satisfied, or in general virtual technique is applied to achieve the same affect, the moduli space of such maps consists of component of smooth manifolds. Counting the zero dimensional components gives a number, denoted by . We then get the composition map

μd:Hom(L0,L1)×…×Hom(Ld-1,Ld)→Hom(L0,Ld)

which is defined by

on generators (here we assume no disk or sphere bubbling for simplicity in this review).

The collection of composition maps gives rise to differential graded structure of morphism spaces and their associative compositions up to higher homotopy. In algebraic language, Fukaya category is anA∞category. That is to say, the composition maps will satisfy someA∞relations, which can be verified by the compactification of the moduli spaces. The standard algebraic process of twisting and deriving is then applied to it, in order to access more structures (admitting more objects and making use of higher dimensional moduli spaces).

Mathematically, the best-understood part of homological mirror symmetry is the Calabi-Yau case. In fact, Kontsevich’s conjecture is for mirror symmetry between Calabi-Yau manifolds. There are rich results on different kinds of Calabi-Yau manifolds. For example, elliptic curve [10], Abelian varieties [11], SYZ fibrations[12-15], Quartic surfaces [16], Products [17], and Calabi-Yau projective hypersurfaces [18-19].

1 The Landau-Ginzburg Model

Mirror symmetry is not confined to the scope of Calabi-Yau manifolds. Further examples includes Fano cases. In physicists’ point of view, especially in Hori-Vafa’s notion, mirror symmetry can be interpreted as the correspondence between the ‘gauged linear sigma model’ and the ‘Landau-Ginzburg model’. In general, Landau-Ginzburg model (LG model) introduces a holomorphic function on a Kähler manifold, to study the geometrical and physical properties of the system. The LG model and the Calabi-Yau version theory are related by Landau-Ginzburg/Calabi-Yau correspondence (LG/CY correspondence). Note that in the closed string version, there is also LG/CY correspondence. The invariants of FJRW theory (constructed in [20-22]) of a certain Witten equation are related to Gromov-Witten invariants of a related object.

The global picture of homological mirror symmetry is a square-shaped diagram:

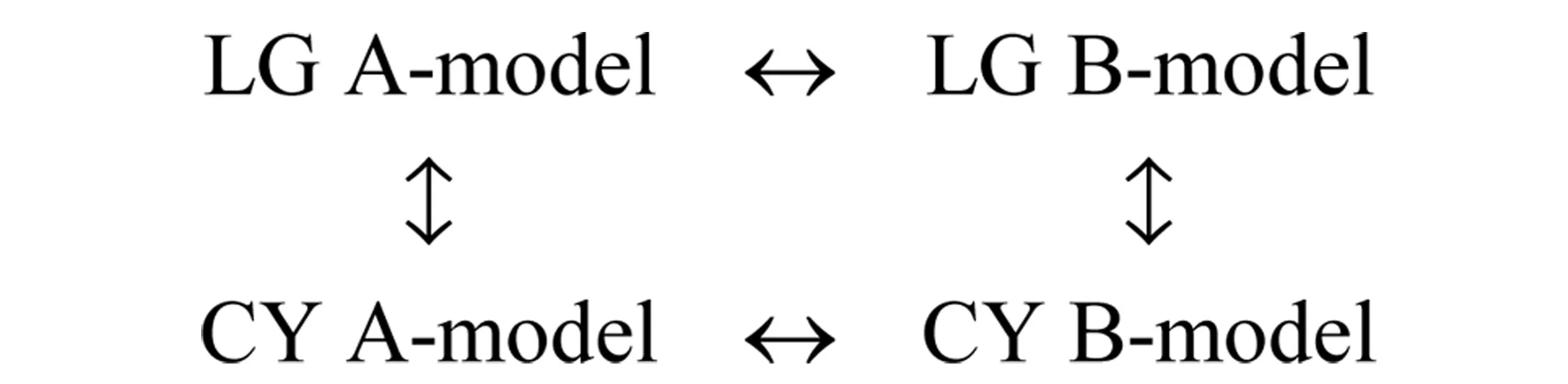
All two-sided arrows here are conjectured to be equivalences. However, this picture is in principle, that in some cases the LG model might not have a CY corresponding part, and the LG-LG mirror symmetry holds for larger class of examples.

In general, the A-models are string theories, which is mathematically about the Lagrangian Floer theory, which are symplectic geometric studies. The B-models are fields theories, which are depicted in bundles and finally sheaves in abstract version. In [23-24], Orlov constructed his open string LG B-model theory, he also established the open string B-model LG/CY correspondence in [25].

In principle, a LG model (M,h,W) consists of a Kähler manifoldMwith metrich, and a holomorphic functionWonM. The physical theory in (2,2) supersymmetry often uses a quasi-homogenous polynomialW, to keep some symmetry of the system, but this can also be generalized. The LG A-model onMis algebraically anA∞category, arising from some Floer-type equation, encoding the information ofW.

The notion of Lefschetz thimble is crucial in our later discussion about this Floer-type equation. So we first elaborate on its definition. For a critical valuew0∈CofW, we can consider pathsγ:[0,1]→Cending inw0, with no intersection with other cirtical values. These paths are called vanishing paths (associated tow0). IfWis holomorphic Morse, we can regard it as a fibrationM→C. Then for a vanishing pathγ, we can naturally define a parallel transportργ. Forx∈W-1(w0), the Lefschetz thimbleB=Bxis defined by

This Lefschetz thimble is a Lagrangian submanifold inM. Given a regular fiberN, and a path going through its base point, the intersection of a Lefschetz thimble withNis called a vanishing cycle. Vanishing cycles aren-1 dimensional, topologically spheres. If we take the vanishing path to be some straight ray parallel to thex-axis inC(instead of segments, we can considerγ:(-∞,0] ( or [0,+∞))→Cand all above construction can be applied), then the Lefschetz thimbleBis just the stable/unstable manifold of the flow, generated by the vector field ▽ReW. Note that, the imaginary part ofWis constant onB.

This setting originates from the LG theory in (2,2) supersymmetry in physics, where the Lefschetz thimbles play the role of the boundary condition for string worldsheet (see Fig.1).

Fig.1 Strings between two Lefschetz thimbles γa,γb,whose images under W are parallel rays, where a and b are two critical points. This picture is from [26]

One can see [26] for more details. In short, in this setting, we consider paths [0,π]→Mwhose ends sit in two Lefschetz thimbles, respectively. In order to consider the ‘supersymmetric ground states’ of the system, a functionalhis introduced, where we rewrite it asαfor our compatibility of symbols:

(1)

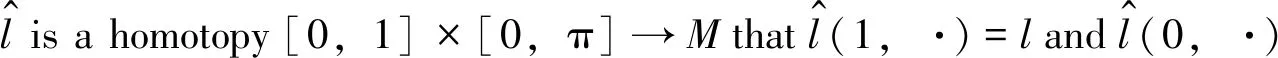
The gradient flow ofαis

∂sφ+J∂tφ=▽ReW(φ)

(2)

In complex version, it is

wherehis the Kähler metric ofM. This is exactly the Witten equation, which is similar to ones in FJRW theory in [20-22]. However, here we must consider equations with boundary. We will discuss it in the next section.

It is worth noting that, the construction of Lefschetz thimbles and vanishing cycles is not only applied to holomorphic Morse functionsW, but can be used to holomorphic Morse fibrationsπ:E→Sfor some Riemannian surfaceS, and we can still get Lefschetz thimbles and Vanishing circles. In Seidel’s construction of Fukaya-Seidel category (see Fig. 2), one considersSto be a unit disc, and connects all critical values ofπto a fixed pointz0on the boundary ofS. Then one takes vanishing circles inπ-1(z0) to be the collection of objects, and gets a Fukaya category inπ-1(z0). The vanishing paths are not canonically chosen, but one can prove some equivalence between different choices. This kind of equivalence is called mutation. One can see [27-29] for reference.

2 Fukaya category of LG model

We need some definitions here, before further discussions. The tuple (M,h,W) is called a Landau-Ginzburg (LG) system, where (M,h) is ann-complex dimensional complete noncompact Kähler manifold andWis a nontrivial holomorphic function onM. We also require thatMis of bounded geometry, using the Kähler metric. If the Kähler formωof the metrichis exact, we call (M,h,W) an exact LG system.

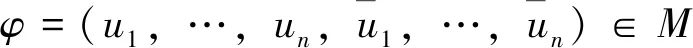
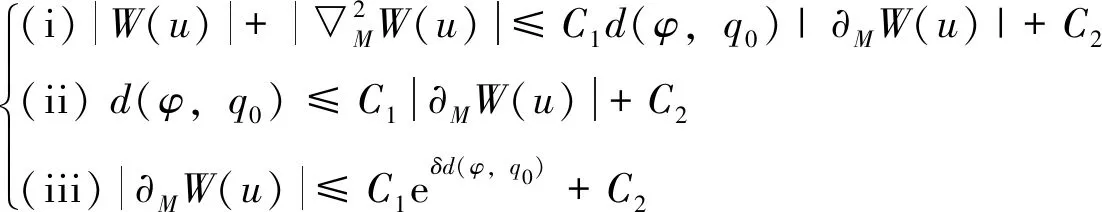
(3)

Another concept we introduce is a regular LG system. IfWis Morse, and for any pairp,q∈CW,p≠q, holds ImW(p)≠ImW(q), then the LG system (M,h,W) is called a regular Morse LG system. A regular tame exact LG system (M,h,W) is a regular LG system, which has exact Kähler formωand satisfies the tame condition.

Note that the condition of exactness will make the functional in (1) well defined.

A Landau-Ginzburg Lagrangian braneL#is a Lefschetz thimbleL, together with a lifti#:L→L#and a Pin structure onTL. These Landau-Ginzburg Lagrangian branes are the objects of our category.

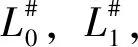
(4)

whose local coordinate form is

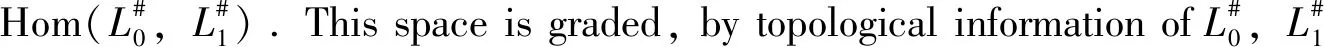
In fact, in order to define ourA∞category, we need to consider strings with different ‘speeds’. That is to say, instead of (4), we need to consider

(5)

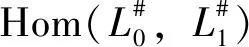
To define composition maps, we must define at first the Witten equation for the pointed discs. Techniqually, to define the equation, we first need a sectionσof the log-canonical bundle of the disc. First,σneeds to be holomorphic. In addition, the imaginary part lmσshould be zero on the boundary. Note that, on strip-like ends, where the part of the disc can be written as [a,+∞)×[0,1] (or (-∞,-a]×[0,1]) for somea>0,σcan be written asκdzfor someκ∈R+in this coordinate.

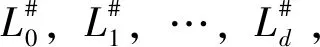
(6)

Here,Zis the perturbation term. Marked pointsz0,…,zdon the boundary divide the boundary circle intod+1 segments. Forli∈SW(Li-1,Li),i=1,…,dandl0∈SW(L0,Ld), we can consider such solutionsφthat the limit ofφ(z) isliwhenz→zi. We also require that the boundary segments are mapped to one of these Lefschetz thimbles, whose order is suitably chosen to make the conditions compatible. Note that, whend=1, we can regard the pointed disc as a stripR×[0,1], and the equation (6) becomes

∂sφ+J∂tφ=κ▽ReW+z(φ)

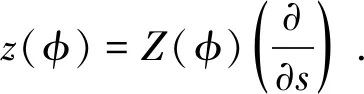
We take the change of the configuration of discs into consideration and find that, for generic perturbations, such maps will make up a smooth manifold of a certain dimension. If the dimension is zero, it is called the rigid one, then counting such maps will give a number . Counting these numbers will give rise to composition maps

where on generators, we have

The symbol * is used to give a sign of the component. By studying the compactness of the moduli spaces, we get theA∞relation (132 of [30])

(7)

where (-1)†μis an integer according to these inputs, which is determined by the coherent orientations of the moduli spaces.

However, the compactness is far from a trivial result. This is because, the targetMis not compact. So we need some kind ofC0estimate. This is done by a mutual control mechanism between theC0bound ofφand |dφ|, for which one can see [30] for the detail. In short, we need to examine the ‘bubbling’ phenomenon where |dφ|→+∞. However, as it is noncompact, we can not get an actual bubble, for no convergence can be obtained if we carry out the bubbling process. Instead, we use some kind of elliptic estimate to control |dφ|, under the condition that the total energy is bounded. In this process, isoperimetric inequality is used (together with the exactness of the symplectic form associated tohand bounded geometry of (M,h)), and the tame condition is also crucial to control the gradient termXRe WImσ+Z(φ).

Summing up, we get the Fukaya category Fuk(M,h,W) of a Landau-Ginzburg model (M,h,W), which consists of the following data:

(i) A set Ob(Fuk(M,h,W)) of objects, consisting of all Landau-Ginzburg branes.

(iii) Composition maps

satisfying theA∞relation (7).

3 More discussion

There are many motivations of the construction of this Fukaya category of LG model. On the other hand, we can also expect to have many applications of this theory. We present a brief discussion in this section.

The readily goal of this construction is to extend the homological mirror symmetry to more general cases. There are already many studies of homological mirror symmetry of LG model, one can see the introduction in [30] for a comprehensive summary. Our Fukaya category of LG model is defined on a general class of Kähler manifolds (exact, with bounded geometry). Once it is defined, we can expect that, it can be used to extend the homological mirror symmetry to more general cases (beyond Fano case).

It worth noting that, if we choose a regular fiberπ-1(w0), we use Seidel’s construction to get a Fukaya-Seidel category Fuk(π-1(w0)). A natural question is the relation between Fuk(π-1(w0)) and Fuk(M,h,W), as they are both A-side theory of LG model. There is no evidence for general relation here. However, in special cases, asCnand (C*)n, we expect there is someA∞quasi-equivalence between them. Some construction is done, in a work in progress by H. Fan, W. Jiang and D. Yang. Furthermore, the Fukaya category of LG model constructed here can be expected to ‘unify’ different constructions for LG A-model ever appeared.

This theory is also related to the quantum singularity theory via Witten equation developed in [20-22] (commonly refered to as FJRW theory), which is a closed string invariant about singularity, constructed by studying the Witten equation on orbifold line bundles on closed Riemannian surfaces. Actually, the construction of LG Fukaya category draws many inspirations from the FJRW theory. In particular, the tame condition we used in the construction above is from there. To go further, we can expect to construct an enriched theory to take both boundary marked points in LG Fukaya category theory, and interior marked points in FJRW theory into consideration. This ‘universal’ theory, once established, can be used to formulate some kind of open-closed correspondence of LG model.

In addition, in Gaiotto-Moore-Witten’s web-based formalism ([31]) of LG theory for holomorphic MorseW, one can consider polytopes generated by singular values ofWinCand secondary fans of all its possible regular polyhedral subdivisions (the dual of which is the space of webs), and establish anL∞-algebra R.One can find the mathematical formulation in the paper of Kapranov-Kontsevich-Soibelman ([32]). The construction there is expected to recover some kind of LG-Fukaya category ( [32,Conjecture 14.10]). In this paper, we are using the same Witten equation as in GMW and KKS, and techniques and viewpoints especially compactness etc. should pave the way to rigorously construct this algebra of infrared and approach this conjecture.