1∶3内共振条件下屈曲梁的准周期运动*

肖龙江，黄建亮

(中山大学航空航天学院，广东 广州 510275)

准周期运动是指系统的振动响应中含有多个不可约频率的运动[1]。当外激励的频率之间不可公度或系统的多个模态之间存在内共振时将会产生准周期运动。准周期运动的存在会导致响应的振幅、频率和相位角随着时间连续变化，使得能量在不同模态之间实时迁移，导致结构的破坏[2-4]。Afaneh和Ibrahim[5]利用多尺度法分析了1∶1内共振条件下两端固支屈曲梁的前两阶振动响应，发现在该条件下屈曲梁可能存在准周期响应。Kreider和Nayfeh[6]通过实验发现，在前两阶模态存在1∶1内共振条件下，两端固支屈曲梁会产生频谱图中存在等间距边频带的准周期运动，Emam和Nayfeh[7]采用数值计算方法验证了上述实验结果。Lau等[8-9]把增量谐波平衡法和多时间尺度法结合起来，用于计算系统的准周期运动。Huang和Zhu[10-11]改进了Lau等[8-9]的方法，用两时间尺度的增量谐波平衡法研究了一端固定一端简支的弯曲梁的准周期运动。在国内，袁铭鸿等[12]研究了耦合系统的准周期运动，从他们得到的准周期运动的频谱图中可以观察到等间距的边频带。张丹伟等[13]用两个时间尺度的IHB法研究了外激励频率不可公约时非线性系统的准周期运动。李小彭等[14]通过数值计算分析了多自由度内共振系统的准周期运动。

本文研究了在基础简谐激励作用下，前两阶对称模态存在1∶3内共振的两端固支屈曲梁的非线性振动。先通过Galerkin方法对梁的振动方程进行离散，然后将传统的单一时间尺度的增量谐波平衡和Floquet理论[15-16]相结合，分析外激励振幅变化时振动方程的周期响应及其稳定性的变化。当梁的周期响应发生Hopf分岔演变为准周期响应时，采用两时间尺度的IHB法研究准周期响应，并验证结果的准确性。

1 两端固支屈曲梁的振动方程

(1)

图1 基础简谐激励作用下的两端固支屈曲梁简图Fig.1 Schematic of a fixed-fixed buckled subject to base harmonic excitation

在此基础谐波激励作用下，由哈密顿原理可求得屈曲梁的振动方程为

(2)

(3)

对方程进行无量纲化，令

(4)

带入方程和边界条件中可得

(5)

y(0,t)=y(1,t)=y′(0,t)=y′(1,t)=0

(6)

其中，点和撇分别表示对时间和空间求导，且

(7)

为了求出静态屈曲函数v(x)，舍去方程(5)和(6)中的时间相关项和外激励项可得

(8)

v(0)=v(1)=v′(0)=v′(1)=0

(9)

(10)

其中，b为无量纲化跨中挠度。把方程(10)带入方程(8)中可解得

(11)

令方程的解为

y(x,t)=u(x,t)+v(x)

(12)

带入方程(5)及边界条件(6)可得

(13)

u(0,t)=u(1,t)=u′(0,t)=u′(1,t)=0

(14)

用文献[17]中的方法求解两端固支屈曲梁的固有频率和模态函数[17-18]。舍去方程中的非线性项、阻尼项和外激励项，可得到方程所对应的线性化自由振动方程，令方程的解为

(15)

由此可得

(16)

(17)

方程(16)的通解为

Φj=c1sinλjx+c2cosλjx+c3sinhμjx

+c4coshμjx+c5cos 2πx

(18)

其中，

(19)

(20)

可得各阶固有频率所对应的模态函数Φj，各阶模态函数满足条件

(21)

其中，δij为狄拉克函数。用Galerkin方法求解方程，为此令

(22)

将式(22)带入方程(13)，在方程两边左乘Φi(x)，并对方程两边从0到1对x积分，可得

=γficos(ωt),i= 1,2,…,n

(23)

其中，

取

ξi=ξ,i=1,2,…,n

(25)

ξ为无量纲化模态阻尼系数，令

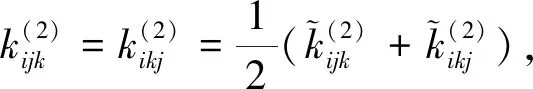
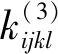
(26)

可将方程(23)化为

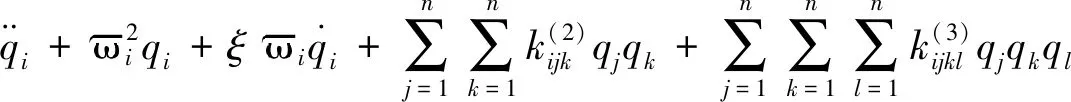
=γficos(ωt),i=1,2,…,n

(27)

2 两个时间尺度的IHB法

用两个新的无量纲时间变量

τ1=ωt,τ2=ωdt

(28)

代替变量t，因此qi(t)变为变量τ1和τ2的函数。

qi(t)=qi(ωt,ωdt)=qi(τ1,τ2)

(29)

由此可得到

(30)

把式(28)、(29)、(30)带入式(27)可得

=γficosτ1,i=1,2,…,n

(31)

式(31)可以写为矩阵形式

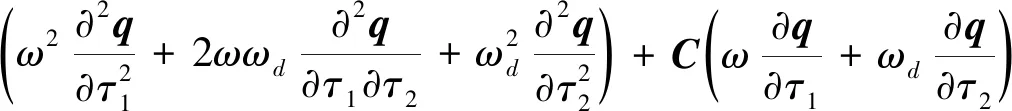
+(K+K(2)+K(3))q=γFcosτ1

(32)

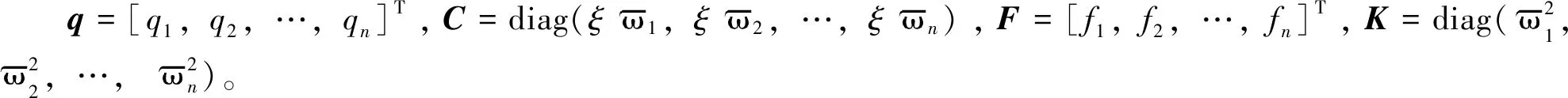
(33)

两时间尺度IHB法的第一步是增量过程。令q0、ωd0和γ0表示一个振动状态，其邻近振动状态以增量形式表示为

q=q0+Δq,

ωd=ωd0+Δωd,

γ=γ0+Δγ

(34)

其中，q0=[q10,q20,…,qn0]T，Δq=[Δq1,Δq2,…,Δqn]T。把式(34)带入式(32)，并且略去高于一阶的小量，可得

(35)

其中

(36)

R是误差向量。当q0、ωd0和γ0是方程(32)的准确解时，R=0。

两时间尺度的IHB法的第二步是谐波平衡过程。因为准周期运动的频谱图在载波频率(频率的整数倍)的周围存在着等间距的边频带，所以可以用Galerkin方法把qi0展开为多重Fourier级数。

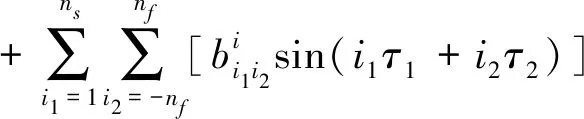
=Cs·Ai

(38)

其中，nc和ns分别为载波频率的余弦项项数和正弦项项数，nf是一个载波频率左侧或右侧所携带的边频带频率的数目，同时

Cs=[C0C1C2…CncS0S1…Sns]

(39)

(40)

其中

C0=[1cosτ2… cosnfτ2]nf+1,

S0=[sinτ2sin2τ2… sinnfτ2]nf,

(41)

Ci1=[cos(i1τ1-nfτ2) … cosi1τ1… cos(i1τ1+nfτ2)]2nf+1,i1=1,2,…,nc

(42)

Si1=[sin(i1τ1-nfτ2) … sini1τ1… sin(i1τ1+nfτ2)]2nf+1,i1=1,2,…,ns

(43)

(44)

(45)

把增量Δqi也展开为多重Fourier级数

Δqi=Cs·ΔAi

(47)

其中，

由此可得

q0=SA, Δq=SΔA

(48)

其中，S=diag(Cs,Cs, … ,Cs)，A=[A1A2…An]T，ΔA=[ΔA1ΔA2… ΔAn]T。

对式(35)运用Galerkin 平均过程可得

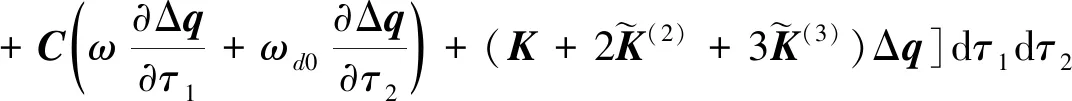
(49)

把式(48)带入式(49)可以产生关于变量ΔA、 Δωd和Δγ的线性方程

(50)

其中

(51)

(52)

其中

方程(50)的未知数数量比方程数量多2，在计算时应先指定两个增量作为控制变量。由于 Δωd无法预先得知，因此应该在向量ΔA中指定两个增量作为控制变量(为了得到准周期解，两个增量不能都是载波频率对应的谐波系数)，指定控制变量后，先令两个增量为0，由式(50)可求解得到 Δωd、Δγ以及ΔA中除了控制变量之外的其他量。把各增量加到原来的解上得到新解，判断新解是否能使误差向量R的模小于给定精度(在本文中，精度为1.0×10-10)；如果不能，把新解带入式(50)，重复上述过程，不断循环直至找到符合精度要求的解。之后，给控制变量加上给定的增量，使循环得以更新，重复上一循环，计算出新情况下的解。

3 计算结果与分析

为了准确反映屈曲梁非线性振动的特性，需要选取足够多的模态数量对振动方程进行Galerkin离散。Emam和Nayfeh[7, 19]的计算表明，对于两端固支屈曲梁，选取前四阶模态进行计算是必要的。本文选取前四阶模态进行计算。

取nc=ns=5，nf=0，Δωd=0带入式(50)可得传统的单一时间尺度的IHB法，以Δγ为增量可计算出周期响应。把周期解的形式由式(38)变为

(55)

其中

(56)

由于

(57)

基础谐波激励只加载在梁的对称模态而未加载在反对称模态上。因此在外激励振幅较小时，系统的反对称模态并未被激发。直至γ增加到0.22时，由于第一和第三模态之间存在1∶3内共振，能量向反对称模态转移，反对称模态被激发，被激发的反对称模态和对称模态所含的频率成分相同。继续增加r值，追踪反对称模态被激发之后的周期响应，并用Floquet理论分析周期解的稳定性。可以发现在r∈[0.27,0.67]时，周期解不稳定，Floquet乘子中有一对复共轭特征值与单位圆相交。因此，在这一段内周期解发生Hopf分岔，演变为准周期解，如图2所示。

图2 ω=37，b=0.002 62时的振幅响应曲线Fig.2 Amplitude response curves whileω=37, b=0.002 62

(58)

其中

(59)

由此，可计算得到准周期响应曲线，如图2所示。准周期运动频谱图的边频带间隔ωd的值也随之计算出来。在本例中，随着γ的增加，边频带间隔ωd逐渐增加，如图3所示。

图3 屈曲梁的准周期响应中ωd随 γ的变化Fig.3 Variation of ωdwithγin the quasi-periodic responses of buckled beam

以γ=0.27时的准周期解为例进行进一步的探究，其第一模态的频谱图如图4所示。从图中可以看出，在载波频率(频率ω的整数倍)周围，存在着等间距的边频带，相邻两个边频带的间隔为ωd≈3.65。ω与ωd的比值是一个无理数，正是这两个频率不可公约导致系统的响应变为准周期运动，使它的时间历程图表现出明显的“拍现象”，如图5所示。从图5还可以看出用IHB法得到的时间历程图与用四阶Runge-Kutta(RK)法的数值结果完全重合。为了进一步验证两时间尺度的IHB法的准确性，图6和图7分别比较了用两时间尺度的IHB法和四阶Runge-Kutta法得到的准周期运动的相图和庞加莱截面图，结果也是完全一致的。从图7可以看出，准周期运动的庞加莱截面图是一条封闭曲线。

图4 ω=37，b=0.002 62，γ=0.27时q1的频谱图Fig.4 Spectrum of q1 while ω=37, b=0.002 62, γ=0.27

图5 ω=37，b=0.002 62，γ=0.27时准周期响应的时间历程图Fig.5 Time histories of the quasi-periodic response while ω=37, b=0.002 62, γ=0.27

图6 ω=37，b=0.002 62，γ=0.27时准周期响应的相图Fig.6 Phase plane portraits of the quasi-periodic response while ω=37, b=0.002 62, γ=0.27

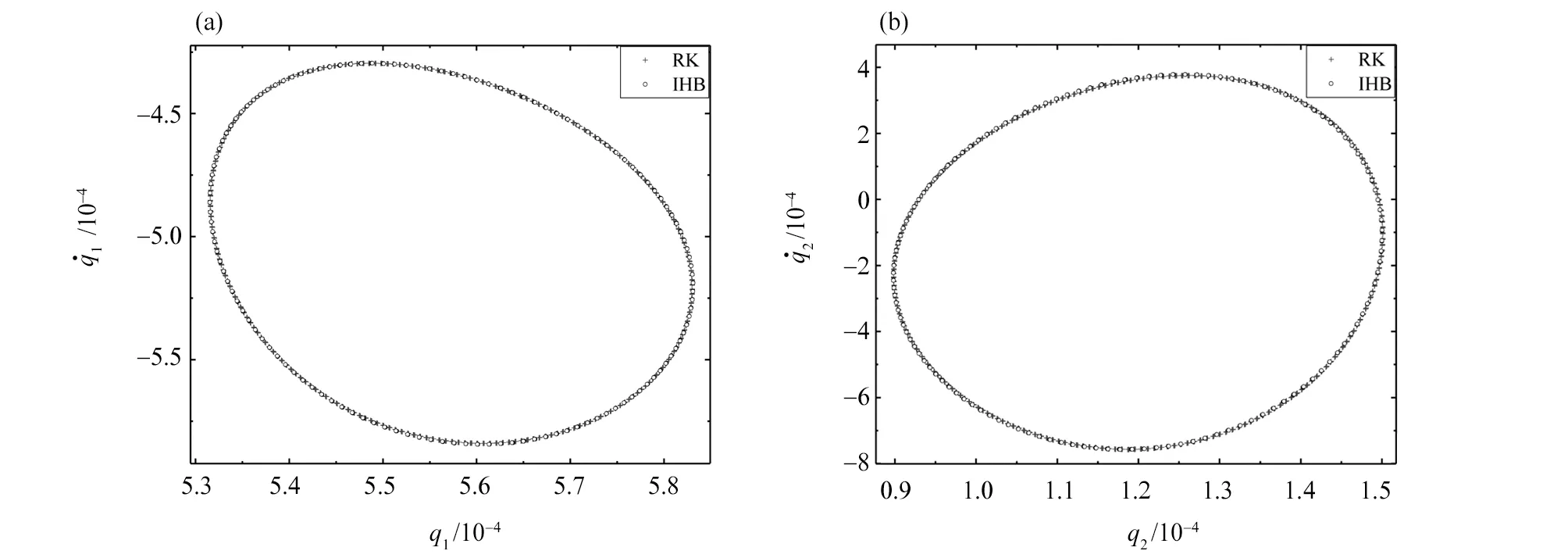
图7 ω=37，b=0.002 62，γ=0.27时准周期响应的庞加莱截面图Fig.7 Poincaré sections of the quasi-periodic response while ω=37, b=0.002 62, γ=0.27

4 结 论

本文用多时间尺度法与IHB法相结合，得到了适用于求解系统的准周期运动的两时间尺度的IHB法。对于前两阶对称模态存在1∶3内共振的两端固支屈曲梁，当作用在其上的基础简谐激励的振幅处于一定范围内时，系统的周期响应会发生Hopf分岔，演变为准周期响应。文中用两时间尺度的IHB得到了屈曲梁的准周期响应曲线图，同时比较了两时间尺度的IHB法和四阶Runge-Kutta法所得到的结果。对比结果表明，两时间尺度的IHB法有较高的精度，适用于解决频谱图中存在的等间距边频带的准周期运动。