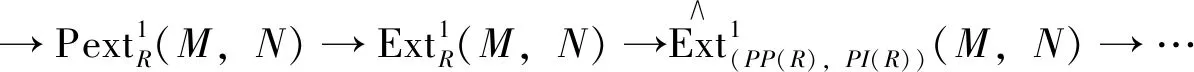Relative and generalized Tate cohomology with respect to balanced pairs

(School of Mathematical Sciences, Chongqing Normal University, Chongqing 401331, China)

Abstract：The relative and generalized Tate cohomology with respect to balanced pairs are studied. An Avramov-Martsinkovsky type exact sequence is obtained.

Key words：balanced pair; relative cohomology; generalized Tate cohomology; Avramov-Martsinkovsky type exact sequence

Throughout this paper, A is an abelian category with enough projectives and injectives. We useP(A) andI(A) to denote the full subcategories of A consisting of projectives and injectives respectively. Let X⊆A be a full additive subcategory which is closed under isomorphisms and direct summands.

The concept of balanced pairs was introduced by Chen[1]. This generalizes the notions of right and left balanced functors, which were introduced by Carten and Eilenberg and were generalized to relative homological algebra by Enochs and Jenda[2]. In fact, these theories are based on the classical balanced pair (P(A),I(A)). Chen showed that for a balanced pair (X,Y) of A, it inherits some nice properties from the classical one[1]. For some work on the balanced pairs please see [1, 3-5].

It is well known that derived functor is a powerful tool in studying homological properties of rings and modules in classical homological algebra. For the classical right derived functor ExtA(-,-) induced by HomA(-,-) simultaneously measures unprojectiveness of the first variable and uninjectiveness of the second one. So we may say the derived functor ExtA(-,-) is based on the classical balanced pair(P(A),I(A)).

The relative homological algebra, especially Gorenstein homological algebra, as a generalization of the classical one, was developed by Enochs and Jenda[2]. It has been developed to an advanced level in recent year and used in the representation theory of algebras and algebraic geometry. In particular, Enochs and Jenda introduced and studied the Gorenstein right derived functor GextA(-,-) over a Gorenstein ring.

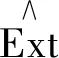
In [7], Iacob gave another way to prove the existence of above exact sequence, and Tate cohomology in the sense of Iacob is more general.

The aim of this paper is to introduce and study the relative and Iacob’s generalized Tate cohomology with respect to balanced pairs. Furthermore, we give the Avramov-Martsinkovsky type exact sequence relative to balanced pairs. Then as applications, many results are generalized and improved.

1 Preliminaries

LetM∈A. A morphismθ:X→Mcalled a right X-approximation ofM, ifX∈X and any morphism from an object in X toMfactors throughθ.The subcategory X is called contravariantly finite if each object in A has a right X-approximation (see [8, P.81] and [9, Def.1.1]). Recall that X is an admissible contravariantly finite subcategory provided that each right X-approximation is epic. It is equivalent to that any right X-acyclic complex is indeed acyclic. Dually one has the notion of left Y-approximation and then the notions of (coadmissible) covariantly finite subcategory.

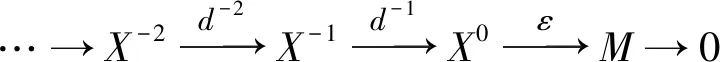
Definition1 ([1, Def. 1.1])A pair (X,Y) of additive subcategories in A is called a balanced pair if the following conditions are satisfied:

(BP0) the subcategory X is contravariantly finite and Y is covariantly finite;

It follows from [1, Cor. 2.3], for a balanced pair (X,Y),then X is admissible if and only if Y is coadmissible. In this case, we say that the balanced pair (X,Y) is admissible.

We list some examples of admissible balanced pairs as follows.

Example1 (i) It is well known that the pair (P(A),I(A)) is an admissible balanced pair. Which we call it classical balanced pair.

(ii) LetRbe a ring and ModRthe category of leftR-modules. By [2, Example 8.3.2],(PP(R),PI(R)) is an admissible balanced pair, wherePP(R) andPI(R) are the subcategories of ModRconsisting of pure projective modules and pure injective modules respectively.

(iii) LetRbe a Gorenstein ring (that is,Ris a left and right Noetherian ring with finite left and right self-injective dimensions). Then by [2, Thm. 12.1.4], we have that (GP(R),GI(R)) is an admissible balanced pair in ModR, whereGP(R) andGI(R) are the subcategories of ModRconsisting of Gorenstein projective and Gorenstein injective modules respectively (see [9-10]).

(iv) LetRbe anFCring (that is,Ris a left and right coherent ring with finite left and right self-FP-injective dimensions). Then by [11, Thm. 3.6], we have that (DP(R),DI(R)) is an admissible balanced pair in ModR, whereDP(R) andDI(R) are the subcategories of ModRconsisting of Dingprojective and Ding injective modules respectively (see [12-14]).

2 Relative cohomology with respect to balanced pairs

They are independent of the choices of theX-resolutions ofMand theY-coresolutions ofNrespectively. For anyn∈Z,we write

and call it the relative cohomology group with respect to the balanced pair (X,Y).

By Example 1, we have the following

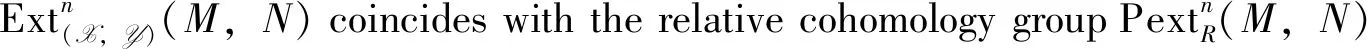
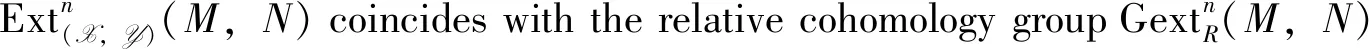
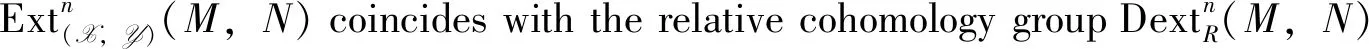
Then it is easy to check the following results of Ext(X,Y)(-,-).

Proposition1 Let (X,Y) be an admissible balanced pair in A andM,N∈A.

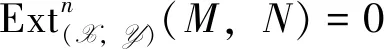
(iii) For any right X-acyclic (equivalent left Y-acyclic) complex 0→A→B→C→0 in A, there exist the following long exact sequences

and

In the following, we want to compare Ext(X,Y)with the classical ExtA.

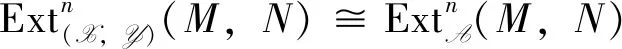
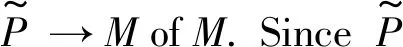
In the case idAN<∞,the proof is similar.

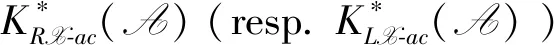
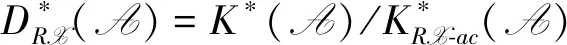
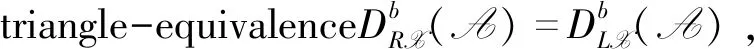
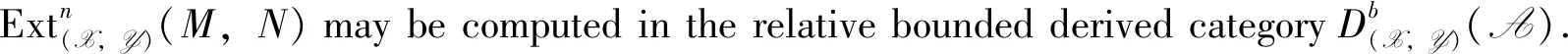
Proposition3 Let (X,Y) be a balanced pair in A. Then for anyM,N∈A andi≥1,there exists an isomorphism of abelian groups:

3 Generalized Tate cohomology relative to balanced pairs

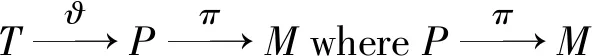
which is independent of choices of resolutions and liftings.

The close relations between absolute, relative and Tate cohomology are illuminated by an Avramov-Martsinkovsky type exact sequence (see [6, Thm. 7.1]) as follows:

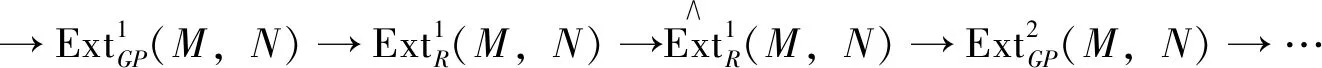
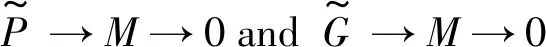
Obviously, Tate cohomology in the sense of Iacob is more general. In this section we consider Iacob’s generalized Tate cohomology relative to balanced pairs.

Definition2 Let (X,Y) be an admissible balanced pair inA andM,N∈A.

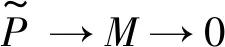
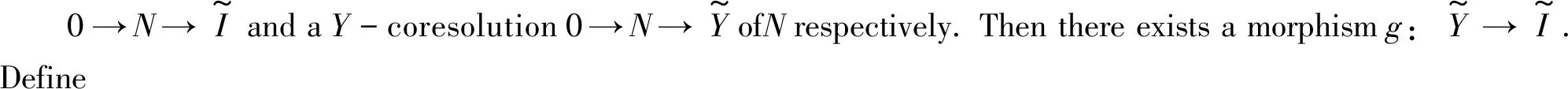
Remark2It follows from [1, Prop. 2.6] and [7, Thm. 1], for anyn∈Z, there exists an isomorphism of abelian groups

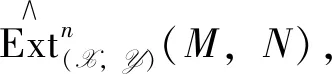
Associate Example 1, we have the following

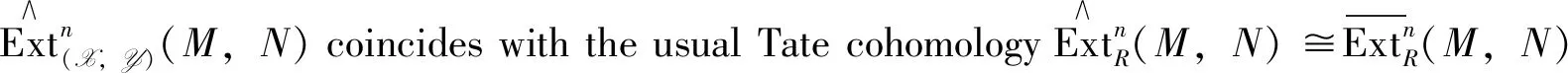
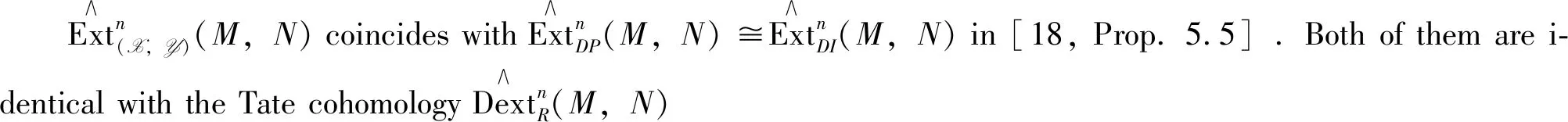
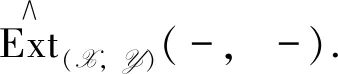
Proposition4 Let (X,Y) be an admissible balanced pair in A andM,N∈A. If 0→A→B→C→0 is a right X-acyclic (equivalent left Y-acyclic) complex in A, then there are exact sequences

and

4 Avramov-Martsinkovsky type exact sequence

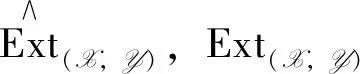
Theorem1 Let (X,Y) be an admissible balanced pair in A andM,N∈A.Then there is an exact sequence

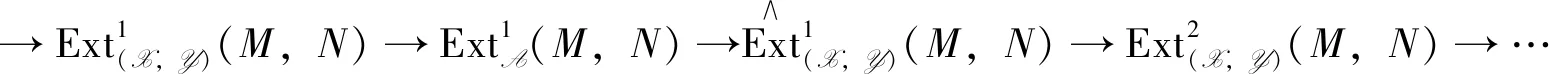
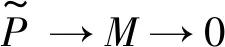
inK(A). By applying HomK(A)(-,N) to it, we get an exact sequence

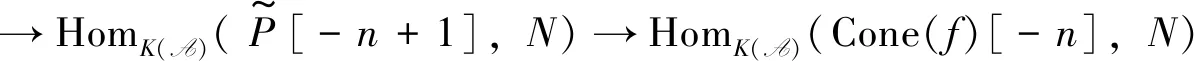
It follows from Proposition 3 that

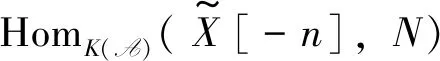
In the following, we give some applications of Theorem 1.

Corollary1 LetRbe a Gorenstein ring. For eachR-modulesMandN, there is an exact sequence

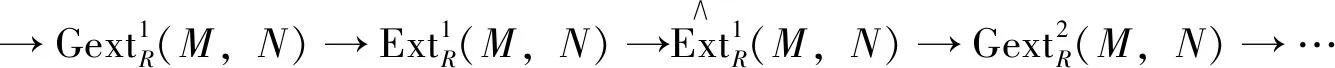
Corollary2 LetRbe anFCring. For eachR-modulesMandN, there is an exact sequence

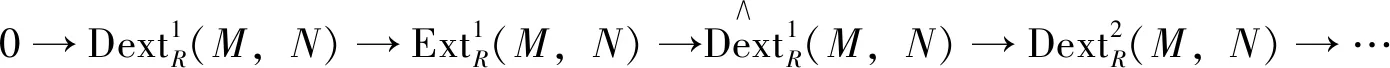
Recall that a leftR-modulePis said to be pure projective, if for every pure exact sequence 0→T→N→N/T→0, Hom (P,N)→Hom(P,N/T)→0 is exact. Thus projective and finitely presented modules are pure projective.

Corollary3 LetRbe a ring. For eachR-modulesMandN,there is an exact sequence