超混沌Tang系统的分析及其线性反馈同步与其电路实现*

高智中

(安徽科技学院信息与网络工程学院，安徽 蚌埠 233030)

当非线性动力学系统具有两个或两个以上的正Lyapunov指数时,系统处于超混沌状态，动力学行为比一般混沌系统更复杂,更难以预测。构造超混沌系统及其同步的研究引起了广大科研工作者的极大关注。文献[1-3]通过施加外部正余弦激励信号而实现超混沌，文献[4-6]通过对三维混沌系统引入一个控制器，并将其耦合到系统的一个方程或多个方程中而实现超混沌。文献[7]设计了一种线性牵制控制器实现了一个参数范围较小的新超混沌系统的同步，文献[8]基于一种新型趋近律研究了分数阶不确定Duffling 系统的自适应滑模同步问题，文献[9]研究了分数阶单摆系统的终端滑模控制混沌同步，文献[10]研究了一类分数阶冠状动脉系统的混沌同步问题，文献[11]研究了主-从蔡氏电路系统在线性状态误差反馈控制下存在通道时延时的滞后混沌同步问题。但是这些方法的控制器设计比较复杂，而且同步收敛速度较慢和对参数敏感。

针对上述问题，本文基于Tang系统[12]，构造了一个新的四维超混沌Tang系统，用数值模拟方法分析了该系统的相图，分岔图和Lyapunov指数谱等基本动力学特性。与以往的超混沌相比，新系统的参数k具有更大的变化范围，并且系统随k与p变化表现出相同的动力性行为且成一定的比例。设计了一种线性牵制控制器实现了该超混沌系统的同步，利用了混沌系统的状态变量的有界性，通过误差系统内部的自组织作用，整个误差系统渐近稳定从而实现了混沌同步，该方法不需要求系统的最大 Lyapunov 指数或建立 Lyapunov 函数，从而大大减少了计算量，而且这种方法容易实现、同步速度快、同步结果稳定。最后设计了相应的实验电路，并在示波器中观察到电路系统的超混沌动力学行为和驱动系统与响应系统的同步结果，这些结果与数值仿真结果基本吻合。

1 超混沌Tang系统及其超混沌吸引子

文献[12]提出的新的三维自治混沌系统，其状态方程可表示为

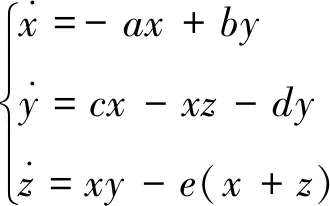
当a=25.6,b=66.8,c=39.22,d=0.2,e=4时，系统存在典型的混沌吸引子。

经过大量尝试，在Tang系统的第1个方程增加一个非线性状态反馈控制器w,并增加一个关于w的一阶微分方程，可得到如下新的四维超混沌Tang系统：

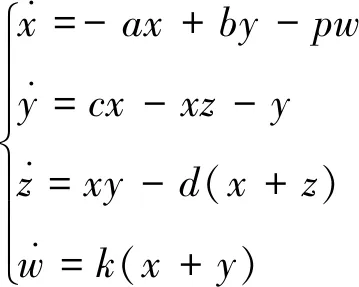
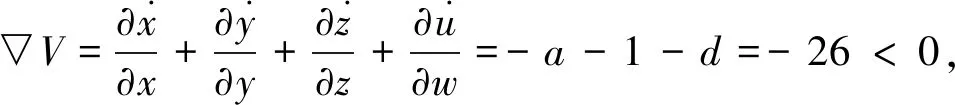
2 动力学行为演化

情形1:当固定a=20,b=35,p=1,c=30,d=5，变量x随k在[0,1 500]变化关于x的分岔图和Lyapunov指数谱图(这里略去了第四根Lyapunov指数曲线)如图2所示。从图2可以观察到,系统具有丰富的动力学行为，并且随参数k变化范围较大。

为了进一步说明系统中取不同参数的超混沌、混沌、周期各自轨迹的特点，本文分别对k=16,64,92,230,410,548,648,1 244,1 498这9个k值上的相轨迹进行数值仿真，图3给出了x-w平面上的典型的相轨迹图，由图可见系统各状态下的相轨迹在不同平面的投影具有不同的形状。表1给出了这9种参数下的Lyapunov指数谱和运动形式。

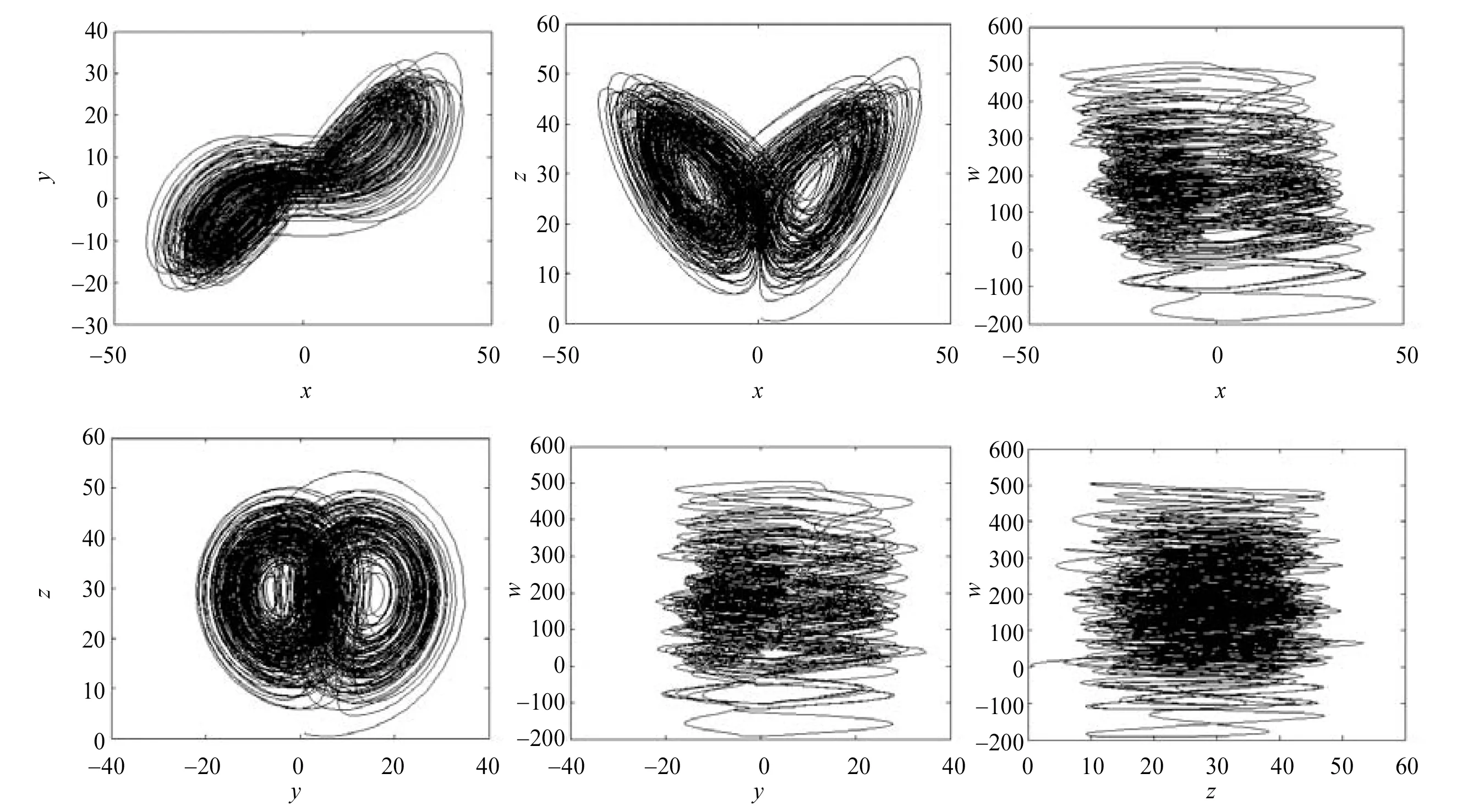
图1 系统的超混沌吸引子Fig.1 Hyperchaotic attractors of system

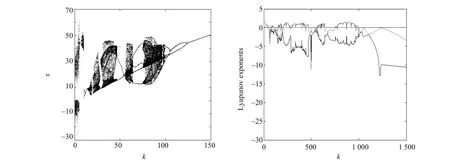
图2 系统随k变化的分岔图和Lyapunov指数谱图Fig.2 Bifurcation diagram and Lyapunov exponent spectrum diagram of the system varies with k

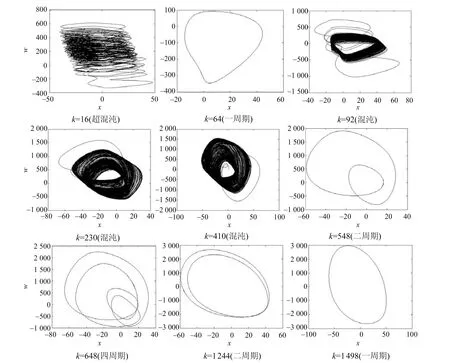
图3 系统各状态下的典型相轨迹在x-w平面上的投影Fig.3 Projections of typical phase paths in the x-w planar graph under different system state

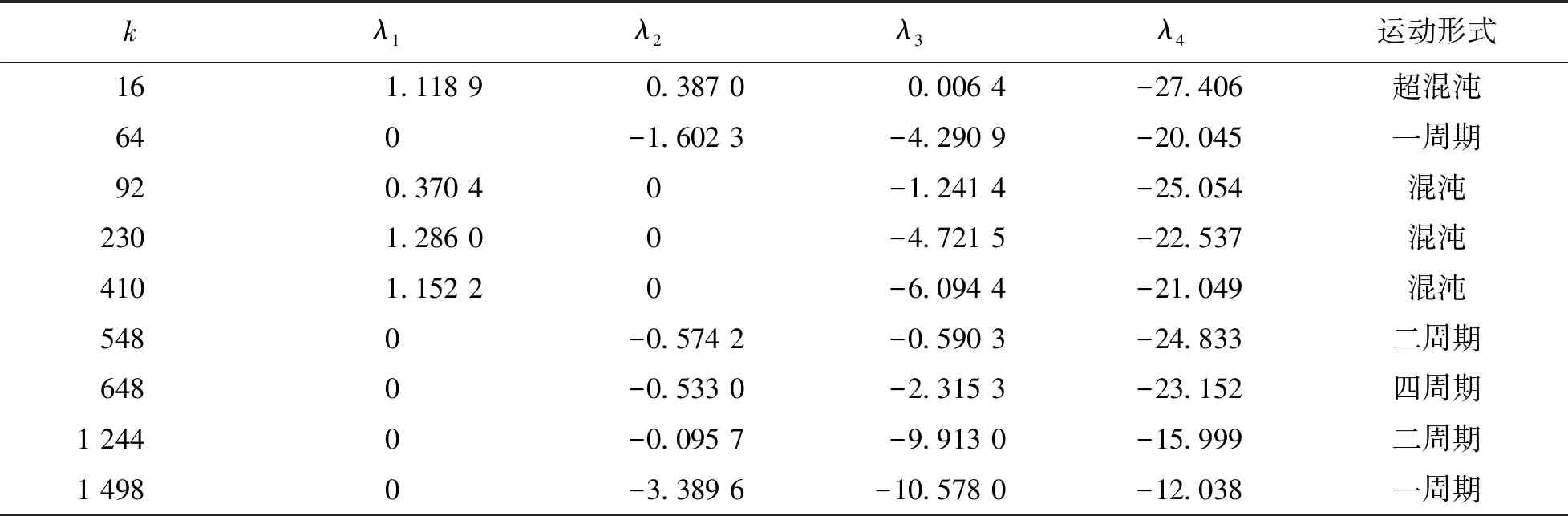
kλ1λ2λ3λ4运动形式161.118 90.387 00.006 4-27.406超混沌640-1.602 3-4.290 9-20.045一周期92 0.370 40-1.241 4-25.054混沌2301.286 00-4.721 5-22.537混沌4101.152 20-6.094 4-21.049混沌5480-0.574 2-0.590 3-24.833二周期6480 -0.533 0-2.315 3-23.152四周期1 2440-0.095 7-9.913 0-15.999二周期1 4980-3.389 6-10.578 0-12.038一周期

情形2:当固定a=20,b=35,c=30,d=5,k=10，变量x随p在[0,150]变化关于x的分岔图和Lyapunov指数谱图(这里略去了第四根Lyapunov指数曲线)如图4所示。由图4见随参数p变化和随参数k变化具有相同的动力学行为,只是变化范围大大的缩小。

图4 系统随p变化的分岔图和Lyapunov指数谱图Fig.4 Bifurcation diagram and Lyapunov exponent spectrum diagram of the system varies with p

3 新超混沌系统的线性反馈同步

设驱动系统为

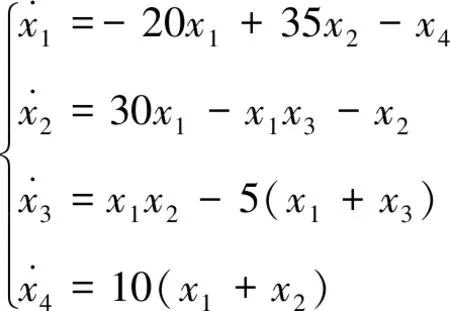
令驱动变量为x2，构造响应系统为

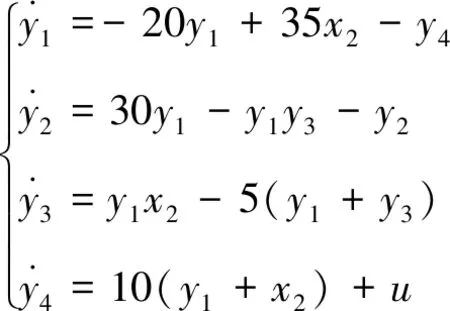
其中u为待设计的线性反馈控制器。

令误差变量为ei=yi-xi,i=1,2,3,4。则两系统的误差系统可化为

选取线性控制器u=-10e1-10e4，则误差系统可进一步化为

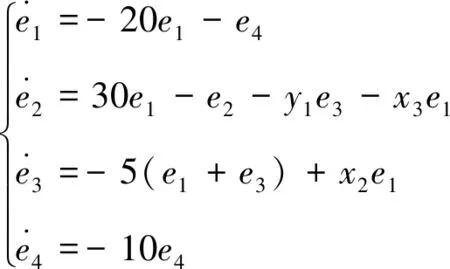
显然e4的解将随着时间以指数速率趋向于零，即当t→∞时，e4→0。同理，e1也能渐近稳定于零点,e2,e3也能渐近稳定于零点，所以整个误差系统就会被牵制到零点，从而驱动系统和响应系统同步。设驱动系统的初始值仍为(10,10,10,10)，响应系统的初始值为(1,1,1,1)，在线性控制器作用下同步误差曲线模拟结果如图5所示，由图5可以看出, 经过一个暂态过程后误差变量e1,e2,e3,e4全部快速趋向于零。

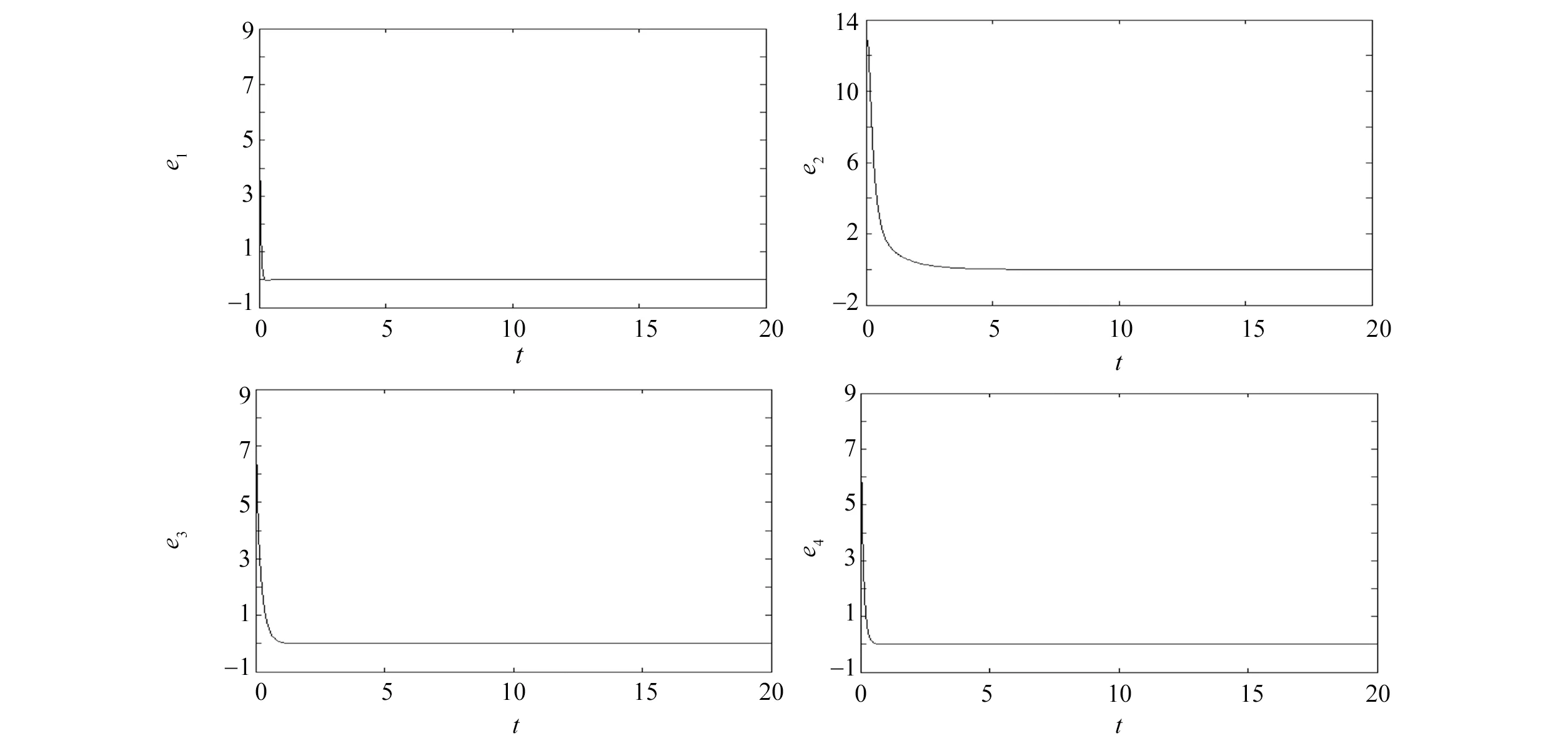
图5 两系统的同步误差曲线Fig.5 Synchronization error curve of two systems

4 电路实现

为了验证驱动系统和响应系统的特性，笔者设计了硬件电路来实现驱动系统和响应系统。因为电路中各电容元件的耐压值是有限的，故将驱动系统中各变量变为原来的1/40,驱动系统表达式变为：

驱动系统电路实现如图6(a)所示，其中参数值为：C1=C2=C3=C4=100 nF,R1=10 MΩ,R2=350 MΩ,R3=3.5 MΩ,R4=100 MΩ,R5=500 MΩ,R6=10 MΩ,R7=7.5 MΩ,R8=3 MΩ,R9=100 MΩ,R10=10MΩ,R11=20 MΩ,R12=2.5 MΩ,R13=1 MΩ,R14=100 MΩ,R15=2MΩ,R16=10 MΩ,R17=10 MΩ,R18=1 MΩ,R19=100 MΩ,R20=R21=1 MΩ,R22=R23=1 MΩ。

图6 超混沌系统的驱动电路(a)和响应电路(b)Fig.6 Driver circuit (a) and response circuit(b) in the hyperchaotic system

利用示波器测量驱动系统的超混沌吸引子如图7所示，与本文的图1对比可见，硬件电路的输出结果与数值仿真结果是一致的。

前文构建了与驱动系统线性反馈同步的响应系统中u=-10e1-10e4,且ei=yi-xi,i=1,2,3,4，故u=10x1-10y1+10x4-10y4，将u的表达式带入响应系统可得：

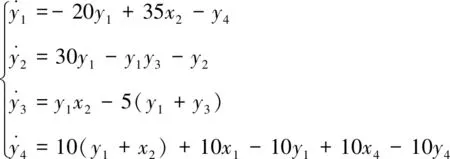
将响应系统中各变量变为原来的1/40,响应系统表达式变为：

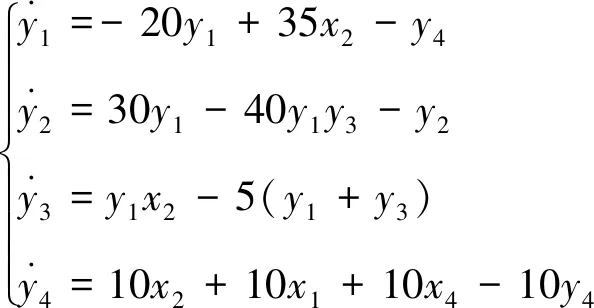
响应系统电路实现如图6(b)所示，为了与驱动系统的参数便于对比，响应系统的参数下标前加了0，各参数分别为：C01=C02=C03=C04=100 nF,R01=10 MΩ,R02=350 MΩ,R03=3.5 MΩ,R04=100 MΩ,R05=500 MΩ,R06=10 MΩ,R07=7.5 MΩ,R08=3 MΩ,R09=100 MΩ,R010=10MΩ,R011=20 MΩ,R012=100 MΩ,R013=1 MΩ,R014=100 MΩ，R015=2MΩ,R016=10 MΩ,R017=10 MΩ,R018=1 MΩ,R019=100 MΩ,R020=10 MΩ,R021=1 MΩ。

驱动系统和响应系统的同步性测试如图8所示，图8(a)所示为x1和y1的时序图，对比x1和y1时序波形图可见，随着时间的变化，波形是相同的；图8(b)所示为x1和y1的状态同步图，可见x1和y1达到了良好的同步，同理，对x2-y2,x3-y3,x4-y4进行相同测试，结果与x1和y1的同步性是一样的。可见，驱动系统和响应系统具有良好的同步性。

图8 超混沌系统的驱动电路和响应电路的x1和y1的时序图和状态同步图Fig.8 Time-serial diagram and state synchronization diagram of x1 and y1 in the driver system and response system of the hyperchaotic system

5 结 论

本文在Tang混沌系统基础上构造了一个新的四维超混沌系统,重点研究了新引入的两个参数k和p取不同值时超混沌系统的运动情况, 通过分岔图、Lyapunov指数谱及相图的数值仿真,刻画了超混沌系统的运动规律，结果发现新的四维超混沌系统具有丰富的动力学行为。成功构造了一种线性控制器实现了该超混沌系统的同步，最后设计了相应的实验电路，并在示波器中观察到电路系统的超混沌动力学行为和驱动系统与响应系统的同步结果，这些结果与数值仿真结果基本吻合。