椭球变换构建工程独立坐标系方法比较*

刘国栋，刘 佳，秦 浩，刘 浪

(重庆交通大学 土木工程学院，重庆 400074)

随着社会现代化的进程，对工程控制的要求呈现出高精度化、大范围化，高精度的GNSS定位技术的发展，很好的满足了这个需求。但工程区域过大会使得区域跨经度范围过大，地形起伏相对高差变大，若仍采用以参考椭球面作为投影面的3°带与6°带国家大地坐标系建立方法，那么高精度将无法保证[1]。故在实际的工程中一般会选择区域内中央经线作为新的中央子午线和改变投影面使用新的参考椭球来建立独立坐标系统，从而满足测区内长度投影变形不大于2.5 cm/km的工程规范[2]。改变投影面目的是将平面坐标归算到区域内的平均高程面上[3]，即通过改变椭球参数，使得变换后的参考椭球面与测区内平均高程面相切，作为新的大地坐标系的投影面。

首先，分析了工程独立坐标系建系原则，供读者选择适合工程实际需求的建系方式，对椭球膨胀法、椭球平移法、椭球变形法原理进行探讨，论述通过椭球变换建立具有抵偿投影面独立坐标系的方法流程，最后，通过算例验证该方法构建独立坐标系对精度提高的可行性，并分析三种椭球变换法建系的差异优缺点，为不同实际工程提供选择参考。

1 工程独立坐标系建系

1.1 工程建系规范

从外业观测值到参考椭球面再投影到高斯平面坐标系的过程中，主要有两次长度变形[4]：

(1)量测边的高程归化，假设量测水准面已经过垂线偏差改正，量测边的平均水准面平行于椭球面，平均水准面与椭球面有一定距离Hm，需要进行高程归化。

(1)

(2)椭球大地线的高斯投影距离改化，椭球面上大地线投影到高斯平面上，需要距离改化。

(2)

为了便于施工放样工作的顺利进行，要求在图纸上量测的边长数据按照比例尺计算的实地边长，应和实地量测的边长在长度上相等[5]。在《工程测量规范》(GB50026-2007)中规定：建立平面控制网坐标系统，应满足测区内长度投影变形不大于2.5 cm/km，相对长度变形小于1/40 000。

1.2 工程坐标系建立原则

根据工程建系规范，结合实际情况选择平面投影建系原则：

(1)在满足工程规范精度要求前提下，根据实际工程区域范围距离国家标准3°或6°带中央子午线不超过45 km，选择标准的国家3°或6°带高斯投影，建立坐标系，有助于工程应用。

(2)若边长的投影归算不能达到精度要求，为保证工程坐标系能满足精度，需要考虑其他方式进行投影：

①更改中央子午线，一般选择工程区域内中央经线作为投影建系的中央子午线，将地面观测结果依然归算到参考椭球面上，即任意带高斯投影[6]；

②更改投影面，建系过程仍然采用3°或6°带高斯投影，但投影面则是选择合适的高程面作为抵偿投影面，一般选择测区范围内的平均高程面，即抵偿投影面的高斯投影；

③既更改中央子午线又更改投影面，即具有抵偿投影面的高斯任意带投影[7]。

实际工程中为追求高精度，多采用具有抵偿投影面的高斯任意带投影建系，将椭球运用某种方法进行变换，使椭球面变换到与原椭球的某一高程面上，再将变换后的椭球控制点按照任意带高斯投影到新椭球的椭球面上，从而达到一定区域范围的投影变形最小化，极大的提高投影精度。

2 变换椭球独立坐标系建系原理

建立与工程区域相适应的投影坐标系，需要先确定合适的参考椭球，椭球都是由椭球参数所确定的，在原符合全球范围的参考椭球的基础上进行变换。不同的椭球变换方法会引起椭球参数如坐标原点、长半轴、扁率以及坐标轴指向等的变化，但一般不会引起坐标轴旋转与尺度的变化[8]。椭球参数的变化会引起大地坐标经度、纬度的变化，大地坐标变化量采用广义大地坐标微分公式可得：

(3)

代入不同平移参数、旋转参数、椭球几何要素以及尺度因子Δm可计算出不同椭球变换方法，主要方法有椭球膨胀法、椭球平移法、椭球变形法[9]。

2.1 椭球变换

2.1.1 椭球膨胀法

椭球膨胀法是保持椭球的扁率α不变、椭球中心点不变，通过增长短半轴与长半轴的长度达到椭球膨胀效果，使得膨胀后的椭球面与目标高程面相切(高程面可能不与椭球面平行，切点称为基准点，下同)[10]，如图1所示。

图1 椭球膨胀法

P点为地面点，E1为原椭球，E2为膨胀后椭球，Ph为投影抵偿面(即指定高程面)，椭球膨胀的过程是将原椭球E1保持扁率α不变，膨胀到投影抵偿面Ph，得到新椭球E2，Δh为P点沿着法线方向E1到E2的距离。因为椭球的各向异性，P点在原椭球中的法线与变换后椭球中的法线不一定会重合，这使得椭球膨胀法的长半轴参数确定出现多种计算方法[11]。本文选用法线方向直接增长法进行椭球膨胀法探讨，把变换前后P点两法线视作重合，故有：

(4)

式中，B0为基准点P点经纬度；Δh为选择抵偿投影面的大地高，即Ph大地高；da为椭球长轴变化量，为使得da=0，短轴相应发生变化。

变换前后空间直角坐标原点没有发生位移，故dX=dY=dZ=0，也没有发生旋转和尺度变化，故εX=εY=εZ=0,Δm=0。由广义大地坐标微分公式(3)可得区域内控制点Pi变化量：

(5)

其中，参数计算如下(后文也如此)：

(6)

2.1.2 椭球平移法

椭球平移法是保持原椭球参数不变，将椭球整体平移到另一位置，使得平移后的椭球面与投影面相切，如图2所示。

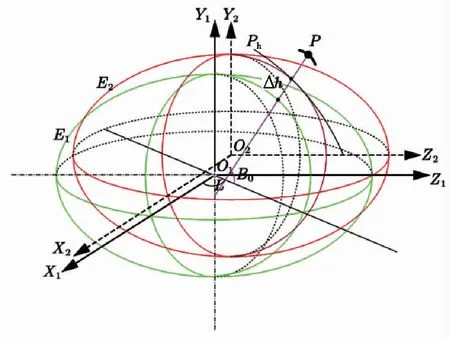
图2 椭球平移法

原始椭球E1保持原椭球几何要素不变，da=dα=0，沿P点的法线平移Δh，与定义投影参考面Ph相切，得到新椭球E2。椭球平移前后的基准点经纬度没有发生改变，只有椭球中心坐标发生变化，即：

(7)

上式可计算椭球中心平移量。由广义大地坐标微分公式(3)可得区域内控制点Pi变化量：

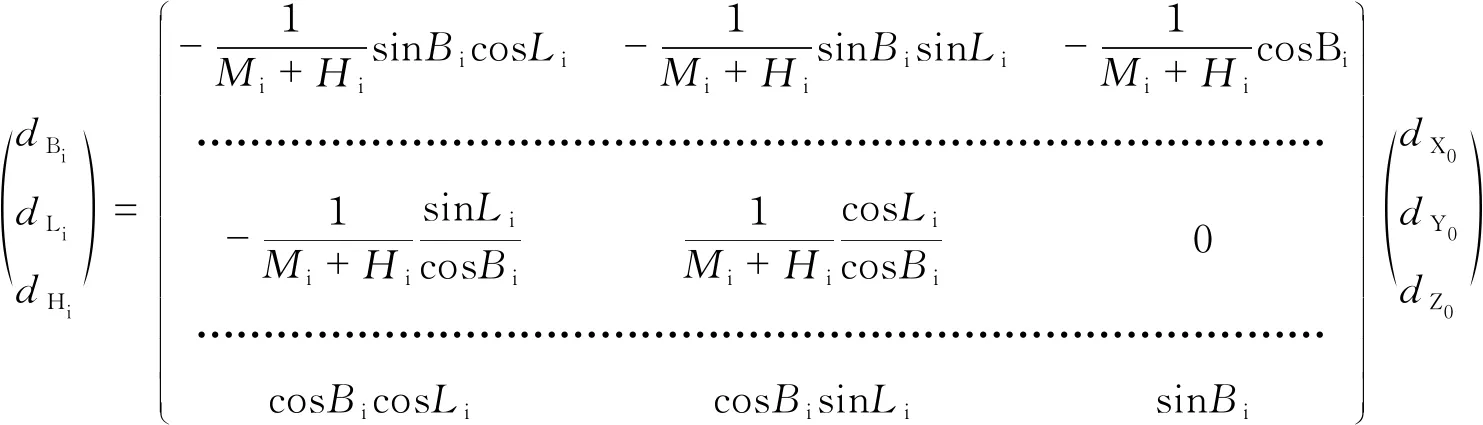
(8)

2.1.3 椭球变形法

椭球变形法是保持椭球中心和坐标轴指向不变，通过改变椭球长短半轴与扁率α，达到膨胀目的，变换前后基准点的经纬度不变，如图3所示。

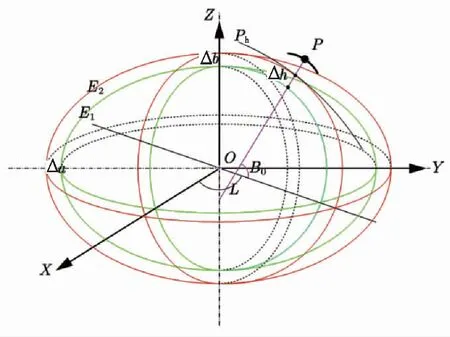
图3 椭球变形法

本文介绍方法是将原椭球E1沿着基准点P点的法线膨胀Δh，使膨胀的椭球面与设定投影面Ph相切，保持椭球中心及坐标指向不变，变换膨胀椭球的扁率dα≠0，使变形后的椭球P点法线与原椭球法线相重合，从而使基准点的经纬度不变，即:

(9)

由广义大地坐标微分公式(3)可得区域内控制点Pi变化量：

(10)

2.1.4 椭球变换比较

三种椭球变换对比，从变换特点、控制点大地坐标变化及适用范围三因素考虑，如表1所示。

表1 三种椭球变换法对比一览表

2.2 椭球变换独立坐标系的构建流程

(1)在工程区域内选择中心点(B0、L0、H0)作为基准点P；

(2)选择区域范围内的平均高程所在高程面作为抵偿投影面(即Ph)，选择椭球变换法计算椭球参数；

(3)将区域内的原控制点Pi在新椭球参数下计算得到新椭球下的控制点坐标；

(4)对新椭球控制点进行任意高斯平面投影，得到平面坐标(x,y)，即独立坐标系建成。流程如图4所示。

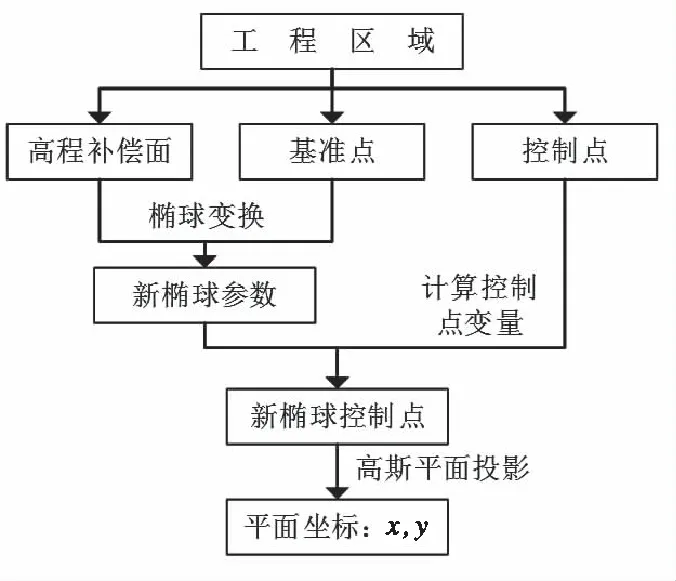
图4 具有抵偿投影面独立坐标系构建流程

3 独立坐标系建立算例分析

为验证建系理论的可行性，设计模拟算例进行验证，编制椭球变换坐标转换程序。设定工程原椭球的参考基准为WGS 84椭球，a=6 378 137,α=1/298.257 223 563，测区基准点P的大地坐标为(28°,107°,250)，工程范围为以P点为中心，经度与纬度在点P的±0.2° 范围，高程在±50 m范围内，随机生成控制点30个，平均高程为250 m。故算例设定中央子午线为107°，高程补偿面Δh=250 m。

本文选择3个点为例进行坐标转换结果分析，三点在原椭球的大地坐标、方位角与大地线如表2所示。其中,P3距离基准点最远达到16 km，最短的距离为P1点7 km，三点分别在基准点的3个方位上具有很好的代表意义。

表2 控制点原椭球坐标、方位角与大地线

椭球变换后控制点大地坐标变化量如表3所示。纬度变化上椭球变形法小于其他两种方法；经度变化上只有椭球平移法有变化；大地高变化则是椭球平移法明显小于其他两种方法。

表3 控制点椭球变换后大地坐标变化量

椭球变换后的大地线大地方位角的变化量如图5所示。三种椭球变换的大地线变化量与大地线呈正比关系，距离越远变化越大；数值上，椭球平移法变化最大，椭球变形法次之，椭球膨胀法最小。大地方位角变化，椭球变形法最大，椭球膨胀法次之，椭球平移法最小，接近0值；趋势上，椭球膨胀法与椭球变形法大地方位角变化量随角度增大呈现正弦函数式周期性变化，而椭球平移法则不稳定。在选择椭球变换的时候考虑两种变化因素的综合影响，因椭球膨胀法的两种变化因素小且更稳定，选择此方法更为理想。

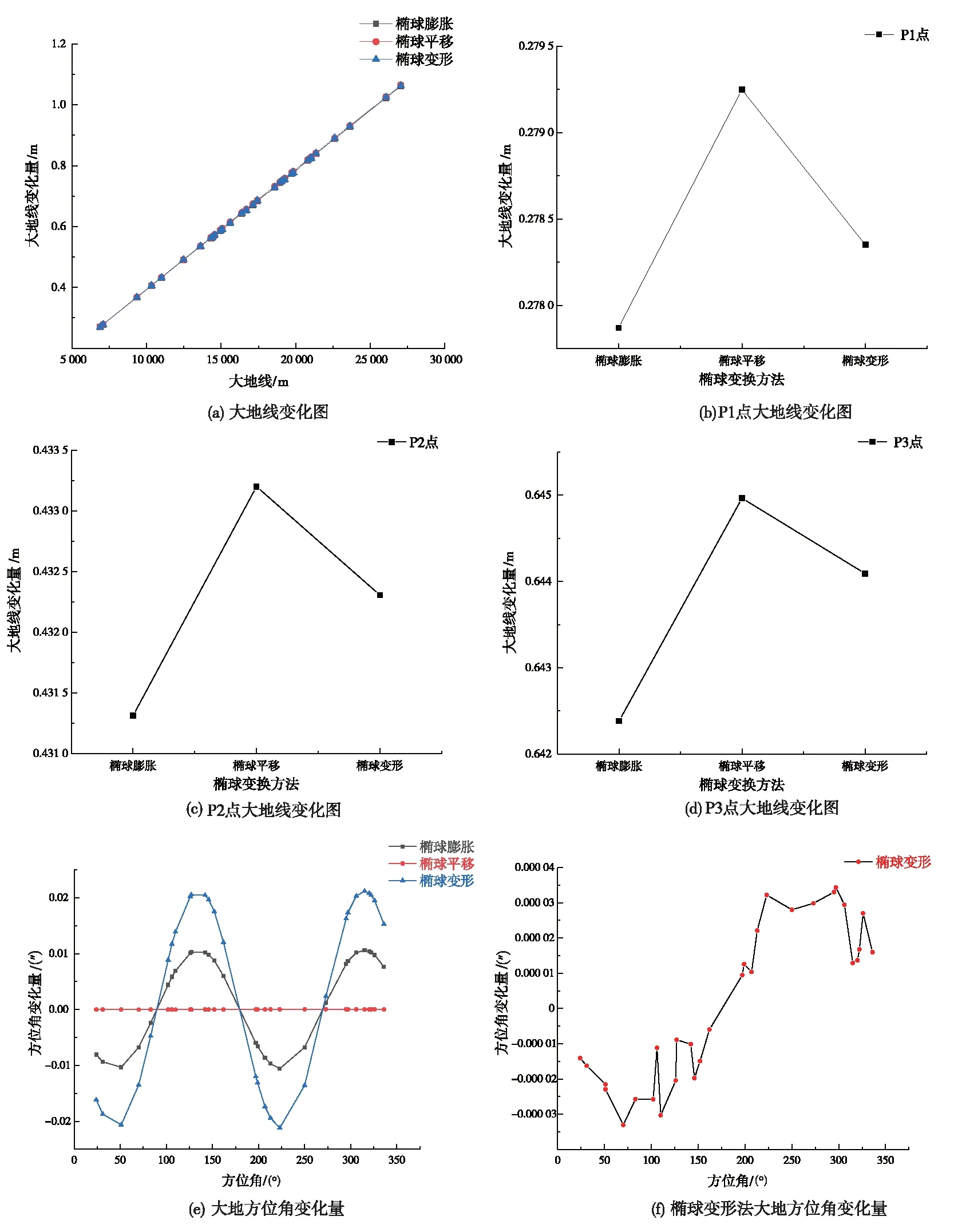
图5 椭球变换后相较与原椭球变化量

若在实验模拟区域内仍采用国家高斯3°带投影，会使长度变形达到12 cm/km，远大于工程规范标准的2.5 cm/km，如表4所示。若采用本文所述三种基于椭球变换构建具有抵偿投影面的高斯任意带投影，建系的平均精度能达到0.9 cm/km，均能很好的满足工程的规范要求。三种利用变换椭球建系方法的投影变形量均与长度距离呈正比关系，距离越远变形越大，三种方法投影变形量基本相当。

表4 边长投影变形对比

4 结 语

本文介绍了三种具有投影抵偿面的独立坐标系构建原理，详述了建系流程，并设计算例实验，分析椭球变换后大地线、大地方位角变化量及变换椭球前后的高斯投影变形量，得出结论如下：

(1)三种利用椭球变换构建独立坐标系的方法，精度不仅明显优于标准高斯投影建系，还高精度满足了工程规范的需求。

(2)椭球平移法计算最为简单，不需要改变椭球的参数，大地高变化较小，但距离与方位角不稳定，适用于需快速实现高斯投影计算时；椭球变形法因控制点大地坐标、大地线变化量较小，很具优势，但是其大地方位角变化量较大，计算相对来说较为复杂，较适用于小区域范围建系；在面对大范围区域选择椭球变换时，针对精度高、变化量小的原则，可以优先选择椭球膨胀法。