浅谈数学学习与非智力因素的关系

陈露

摘 要：孩子学习不良一直是家长们烦恼的问题，也一直是众多教师以及教育学家们所要研究的问题。在众多研究下，对于学业不良的产生，作出分析，所得出的结论是：学生学习困难的主要因素是非智力因素造成的。有的时候，在日常学习中，也经常能看到类似的情况：有的学生感觉很聪明，但是数学成绩总是不好，而有的孩子看似驽钝，在数学成绩上却是名列前茅，造成如此反差的一个重要原因就在于非智力因素。

关键词：数学学习;非智力因素;对策

非智力因素的提出由来已久，教育学家们也一直致力于此项的研究，已形成了一套完整的理论。但在我国现行的教育制度下，一线的教育工作者们对此重视度并不高，所以对于非智力因素对于孩子学习的影响仍有深入研究和落实的必要，如此，方能让学生做到真正意义上的好学。所以，在这里，我们将对非智力因素对于数学学习的影响进行研究，探讨老师如何利用非智力因素充分地调动学生学习的动机、兴趣以及情绪，进而帮助学生更有效地意识到自我调控的重要性，并能够自我调控非智力因素的水平。

随着现代化教育的普及，我国也越来越重视素质教育，素质教育的落实已成必然之势，也同样得到了社会各阶层的共识，而非智力因素的培养正是素质教育落实重要的一部分。

一、非智力因素与学习关系

由心理学的研究可知，一般情况下，非智力因素与学生的学习有着十分紧切的关系，主要体现在：

1.学习和动机的关系

动机指能够激发人进行某一种行为活动，并且能够让该行为活动朝着某一方向成为发展的动力。而学习动机则是学生进行学习活动并且要将之维持下去的心理状态。

2.兴趣和学习的关系

人们能够主动地认识世界，渴望获得知识的意识倾向的来源是学习兴趣。从某种角度而言，兴趣是学生学习的源动力。

3.学习与情感的关系

情感指人们对于外在事物的评价出的价值是否满足自己的需求与想法，从而产生出的一种体验，其主要是通过受教育影响产生的一种非智力因素。

4.学习与意志的关系

意识的能动作用为意志，人们有目的、自发地进行某种行为的一种心理过程。

二、数学学习中非智力因素的作用

非智力因素对于学习的作用与智力因素相比，有着明显的不同，主要可概括为动力作用、调节作用、补偿作用、定向与引导作用。

我们所做的很多事情都需要源动力，而非智力因素之所以能够影响到学生的学习，动机作用就是其中的源动力，学生能够实现自主学习其途径就是动机的刺激。任何事物的发展都需要动力，人的学习亦是同样，当人们对于学习有着强烈的动机的时候，那么也就愈加勤奋，其作为也愈发果断，而且行动的时间更具有持久性，这样才能自主地去进行探索，学生的智力方能因此得到提高。

但人们的生活总是有着诸多的环境影响，人不是一种独立的个体，总是在与外界接触，而接触后的结果之一就有情绪上的影响，或高兴，或悲伤，或愤怒，而这些喜怒哀乐的情绪又都是能够影响人们在生活中做的下一件事情的，所以很多学生的学习效率不高，抑或是学习兴趣不大，很大程度是受了情绪的影响，而其中的负面情绪对于我们的学习所产生的则是负面的作用，而非智力因素中包含有情感，这样就需要利用非智力因素对其进行调节，方能有效地发挥智力因素，提高学习效率。

我国自古的教育理念之中就有勤能补拙之说，而且纵观历史，天资不高但后来能够事业有成抑或是学业有成者不在少数，这其实就是一种非智力因素对于智力因素的补偿，也就是补偿作用。勤奋努力的人因为刻苦等诸多因素，通过不断地磨炼总能弥补先天上的一些不足。

人们在做某一件事情的时候总是要先确立目标，有目标的人总是能够更加专注地完成某项任务，从而达到事半功倍的效果，而非智力因素正是帮助人们确立目标，引导方向，并让学生始终朝着那一学习目标而努力。

数学这门学科就其本身而言，并无这些外在的因素可言，它本身是一门逻辑严谨的科学学科，但是，人们在学习的时候，非智力因素总是能够起到一个外在的影响作用，而且影响甚巨，所以必须对非智力因素有着高度的重视。

三、非智力因素造成数学学习的不佳情况表现

1.审题不仔细

例1.已知关于x的一元二次方程x2+2x+2k-4=0有两个不相等的实数根。

（1）求k的取值范围;

（2）若k为正整数，且该方程的根都是整数，求k的值。

这一道题目并不难，第一问很好解，只需要通过公式Δ=b2-4ac即可得到所要求得范围;第二小问亦也不难，但是相对于第一问则有相对多的人开始出错，究其原因则在于方程的根是整数这个条件没有注意到，使得最后所得的答案多出一解。

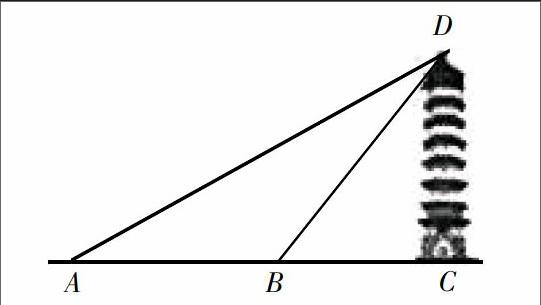
例2.如下图，从点A仰望点D，视角为30°，在点B处观察时，仰角又为60°，且AB为50m，那么CD的长大约是多少米？（精确到0.1m，人的身高可以忽略不计，≈1.732）

这道题目很多学生最后给出的结果都是25，单从这个结果来分析，可以知道学生的想法思路是对的，而错的原因则在于没有看到括号内的条件，这类学生很多都是读题没读完，觉得题目可以做了就直接算出了答案，殊不知后面还有附加的额外条件。

例3.问-2的相反数的倒数是什么？

这是一道十分基础的题目，所容易造成学生错误的是题目理解的错误，会有学生写出答案：2。而造成这一错误的原因很大一部分原因是学生会跳着读题，省略了题目中的某些字，只看到了相反数和倒数这两个条件。

例4.有x的一元二次方程（a-1）x2+x+a2-1=0的其中一个根为零，那么a的值为多少？

这道题容易错解成为+1或-1，若是学生思路正确，方法也得当，并且看到了其中一个解是0，那么能得到这两个解，但却是忽视了题目中的隐形条件，题目中指出了这是一元二次方程，而我们知道一元二次方程的二次项系数是不能为零的，否则，二次项不存在，则不为一元二次方程。

2.表达不规范

例5.如下图，点P在菱形ABCD的对角线BD上，而PE⊥AB，E为AB上的一点，PE=4 cm，那么点P到BC的距离是_____。

题目中给出的条件里面，是有单位的，那么在我们写出答案的时候同样也要给出单位，这题容易漏掉单位，很多学生只是单单写了一个4在上面，最后连怎么错的都不知道，正确的答案应该写为4 cm。

例6.现有甲乙两个火车站，它们之间的距离为1280 km，火车提速后，火车现行驶速度是原来的速度的3.2倍，而两站通行所花费的时间缩短为11个小时，求火车提速后的速度。

这题常见的错误有以下两种，一种是：设火车提速后的速度是x;另一种是：设火车速度是x千米/小时。第一种设的方式的错误在于没有带上单位，而第二种的错误则在于他根本就没有说明白他说的那速度究竟就是提速之前还是提速之后，所犯的错误也相同，都是语言表述不规范，正确的表述方式为：设火车提速后的速度为x千米/小时。

这是一道计算题，一些学生拿到手以后的第一反应就是等式两边同乘以（x-3），化简为2-x=x-3+1，最后解的结果为：x=1。这样的做法看似正确，其实不然。我们一般解分式方程为以下几个步骤：第一步，等号两边同时乘以它们的公分母，这样，能将分式化为等式。第二步，解出等式方程。第三步，将所得到的根带入到分式中进行验证。第四步，得出结论。由此，我们可以看出一般学生经常会遗忘后面的两个步骤，也就是代入检验。而本题将x=1代入以后，经过检验，方能确定这才是原方程的根。

参考文献：

[1]邵文祥.浅谈数学教学中学生非智力因素的培养[J].中小学生教学研究，2011（05）.

[2]刘美蓉.非智力因素的结构探索及培养策略研究[D].贵州师范大学，2008.

[3]陶军.浅谈非智力因素与数学教学[J].数学学习与研究，2013（06）.