关注数学历史考场蓬荜生辉

☉浙江省杭州市文海实验学校　唐剑琴

关注数学历史考场蓬荜生辉

☉浙江省杭州市文海实验学校唐剑琴

数学是一门古老的科学，同时也是一种文化，是人类智慧的结晶，她有着丰厚的历史底蕴，在其漫长的发展过程中，必然会产生许多值得纪念的历史人物、故事等，承载着德智双馨的功能.正如我国著名教育家傅鹰教授所言：“科学只能给我们知识，而历史却能给我们智慧.”若能适时地采撷历史之“珠”来光耀我们的课堂，可以使教学不只局限于现成知识的静态结论，还可追溯它的渊源和动态演变，学生会在欣赏历史人物、品味历史故事、触摸大师的光辉足迹抑或成败的同时唤起对数学的学习兴趣，涤荡自己的心灵.殊不知，新课程改革以来的中考考场也加强了数学史知识的渗透，引领学生关注历史、关注发展.以下采撷近几年的考题作一解析，以飨读者.

一、赵爽弦图

例1（2014年山西）如图1是赵爽为《周髀算经》作注解时给出的“弦图”，它解决的数学问题是（）.

A.黄金分割

B.垂径定理

C.勾股定理

D.正弦定理解析：这是直接对数学史的考查，答案C.

二、斐波那契数列

例2（2007年陕西）小说《达·芬奇密码》中的一个故事里出现了一串神密排列的数，将这串令人费解的数按从小到大的顺序排列为：1，1，2，3，5，8，…，则这列数的第8个数是_________.

解析：观察这一列数，从第三个数起，该数为前两个数的和，这就是“斐波那契数列”，依此规律，第7个数是8+5=13，第8个数是13+8=21.

三、莱布尼茨三角形

例3（2013年哈尔滨）世界上著名的莱布尼茨三角形如图2所示，则排在第10行从左边数第3个位置上的数是（）.

图2

解析：先来观察此三角图的规律：（1）每个分数的分子都是1；（2）从上至下，每一行都比上一行多一个分数；（3）每一行左右两边的数对称；（4）从上至下，两端的数依次是，…；（5）任意一个分数都等于下面两个相邻分数之和.照此规律，第8行第1个数是第9行第1个数是，第2个数是；第10行第1个数是，第2个数是，第3个数是.故选B.

溯源：本题直接搬用“希望杯第4届全国青少年数学大赛7年级初赛第6题”，2007年济南市中考也直接搬用了此题.

四、馨折形

例4（2007年山西）毕达哥拉斯学派发明了一种“馨折形”填数法，如图3所示，则“？”处应填______.

解析：观察九宫图各行的三个数，易发现：2=1× 2，14=7×2，，5=1×5，15=3×5，35=7×5，这就是说：第2列的各数是前面一个数的2倍，第3列的各数是最前面一个数的5倍.所以“？”处的数应是3×2=6.

图3

五、巴尔末公式

例5（2007年自贡）一个叫巴尔末的中学教师成功地从光谱数据，…中得到巴尔末公式，从而打开了光谱奥秘的大门，请你按照这种规律，写出第n（n≥1）个数据是___________.

六、三角形数

例6（2007年河池）古希腊数学家把1，3，6，10，15，21，…，叫做三角形数，根据它的规律，则第100个三角形数与第98个三角形数的差为_______.

解析：观察给定的这一列数可以发现：第2个数比第1个数大2，第3个数比第2个数大3，第4个数比第3个数大4，…，以此类推，第n个数比第n-1个数大n.设第100个数为a，第99个数为b，第98个数为c，则第100个三角形数与第98个三角形数的差为a-c=（a-b）+（b-c）=100+99=199.

七、圆材埋壁

例7（2006年湖北）“圆材埋壁”是我国古代著名数学著作《九章算术》中的问题：“今有圆材，埋在壁中，不知大小，以锯锯之，深1寸，锯道长1尺，问径几何？”用数学语言可表述为：“如图4，CD为⊙O的直径，弦AB⊥CD于点E，CE=1寸，AB＝10寸，则直径CD的长为”（）.

A.12.5寸B.13寸

C.25寸D.26寸

解析：设直径CD的长为2x，则半径OC=x，因为CD为⊙O的直径，弦AB⊥CD于点E，AB= 10寸，所以10=5寸.如图5，连接OA，则OA= x寸，根据勾股定理得x2=52+（x-1）2，解得x=13，CD=2x=2×13=26（寸）.故选D.

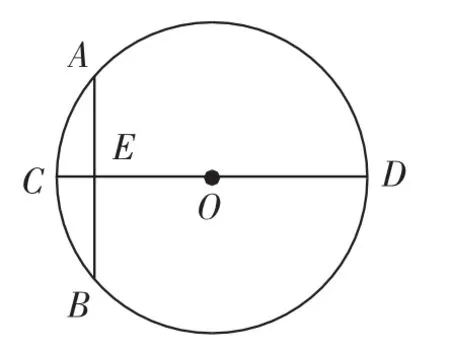
图4

图5

八、高斯速算

例8（2012年黄石）“数学王子”高斯从小就善于观察和思考.在他读小学时就能在课堂上快速地计算出1＋2＋3＋…＋98＋99＋100＝5050，今天我们可以将高斯的做法归纳如下：

令S＝1＋2＋3＋…＋98＋99＋100，①

S＝100＋99＋98＋…＋3＋2＋1，②

①＋②有2S＝（1＋100）×100，解得S＝5050.

请类比以上做法，回答问题：若n为正整数，3＋5＋7＋…＋（2n＋1）＝168，则n＝________.

解析：我们知道，高斯是德国著名的数学家，他和牛顿、阿基米德被誉为近代三大数学家，高斯有“数学王子”之称.他幼年时就表现出超人的数学天才，他面对1到100的求和问题的应对策略，反映出高斯从小就注意把握本质的数学方法这一特点.至于我们面前的问题，根据题目提供的信息，找出规律，列出方程求解即可.

设S=3+5+7+…+（2n+1）=168①，则S=（2n+1）+…+ 7+5+3=168②，①+②得，2S=n（2n+1+3）=2×168，整理得，n2＋2n－168=0，解得n1=12，n2=－14（舍去）.故填12.

九、鸡兔同笼

例9（2014年泉州）“鸡兔同笼”问题是我国古代的数学名题之一，《孙子算经》中记载的题目是这样的：“今有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔各几何？”同学们你得出的这个古代名题的结果是（）.

A.鸡23只，兔12只B.鸡12只，兔23只

C.鸡14只，兔21只D.鸡15只，兔20只

解析：鸡兔同笼问题，在小学可用算术法确定其解，是对学生思维品质考查的优质题目.对初中学生而言，选设好未知数用方程可轻松拿下.设鸡有x只，则兔为（35-x）只，据题意得2x+4（35-x）=94，解得x=23，兔有35-x=12，即鸡有23只，兔12只.故选A.

十、三斜求积与海伦公式

例10（2005年台州）我国古代数学家秦九韶在《数书九章》中记述了“三斜求积术”，即已知三角形的三边长，求它的面积.用现代式子表示，即为：（其中a、b、c为三角形的三边长，S为面积）.①

（1）若已知三角形的三边长分别为5、7、8，试分别运用公式①和公式②，计算该三角形的面积S；

（2）你能否由公式①推导出公式②？请试试.

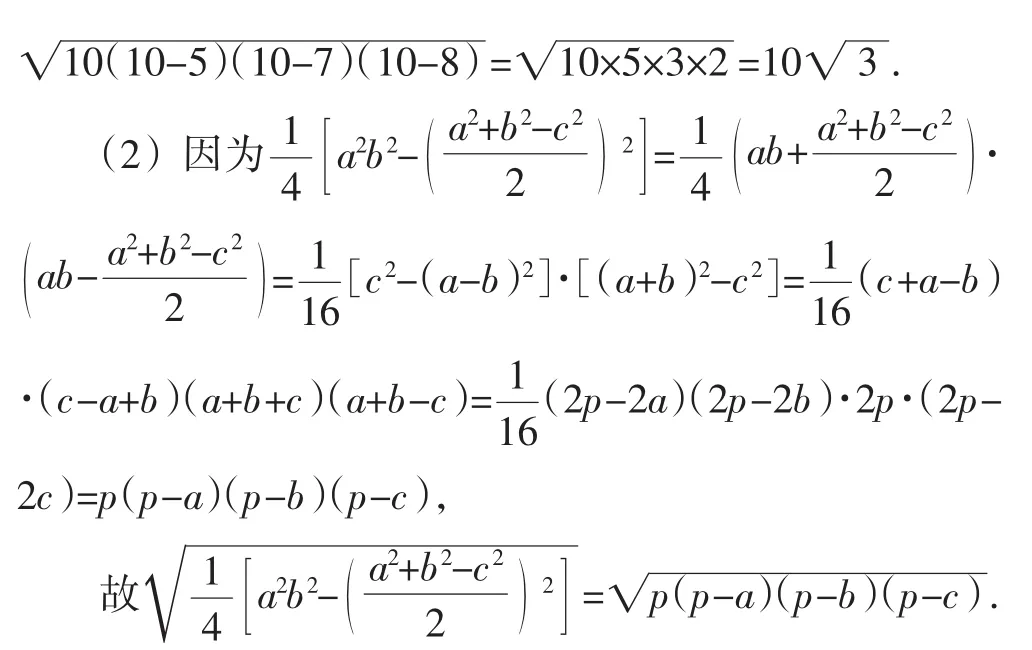
十一、三等分角

例11（2005年佛山）“三等分角”是数学史上一个著名的问题，但仅用尺规不可能“三等分角”.下面是数学家帕普斯借助函数给出的一种“三等分锐角”的方法（如图6）：将给定的锐角∠AOB置于直角坐标系中，边OB在x轴上，边OA与函数的图像交于点P，以P为圆心、2OP为半径作弧交图像于点R.分别过点P和R作x轴和y轴的平行线，两直线相交于点M，连接OM得到∠MOB，则∠MOB=∠AOB.要明白帕普斯的方法，请研究以下问题：

（2）分别过点P和R作y轴和x轴的平行线，两直线相交于点Q.请说明Q点在直线OM上，并据此证明∠MOB=

（3）应用上述方法得到的结论，你如何三等分一个钝角（用文字简要说明）.

（3）以下方法只要回答一种即可.

方法一：利用钝角的一半是锐角，然后利用上述结论把锐角三等分的方法即可.

方法二：也可把钝角减去一个直角得一个锐角，然后利用上述结论把锐角三等分后，再将直角利用等边三角形（或其他方法）将其三等分即可.

方法三：先将此钝角的补角（锐角）三等分，再作它的余角.

数学史开拓了中考命题的市场，使得中考富有情趣，让学生在用其所学知识的同时，了解了历史、增强了认识、感悟到数学的价值所在，我们期待数学史增亮中考.

图6