基于多误差源耦合的五轴数控铣床加工误差综合预测及评判

王　伟　郑从志　张　信

1.电子科技大学,成都,611731　　2.成都飞机工业(集团)有限责任公司,成都,6100923.中国电子科技集团公司第三十研究所,成都,610041

基于多误差源耦合的五轴数控铣床加工误差综合预测及评判

王伟1,2郑从志1张信3

1.电子科技大学,成都,6117312.成都飞机工业(集团)有限责任公司,成都,6100923.中国电子科技集团公司第三十研究所,成都,610041

在综合考虑机床动静态多种误差源的基础上，建立了各运动轴伺服运动模型和多体联动模型，给出了刀具的实际运动位置和姿态，基于包络理论求解了曲面加工实际成形面，对比理想数学模型，对加工误差进行了综合预测和评判。以复杂非可展曲面——S试件为例，给出了S试件的铣削精度构建方法，分析了机床动态因素(位置环、速度环等)对零件铣削精度的影响，并通过切削实验后的数据回归分析予以验证。建立了基于神经网络的机床铣削误差辨识模型，用于评估机床加工后的状态。该平台的搭建为实现大型、关键零件的加工精度预测和保障提供了技术支撑。

动态误差；精度建模；精度预测；航空整体结构件；多轴数控机床

0　引言

数控机床是高端装备制造的重要组成部分，为保证零件的加工质量，提高生产效率，国内外制造企业普遍采用多轴机床高速加工的方法进行零件加工。然而，ISO标准中对于机床的精度校验仅限于静态或低速条件下的几何精度和定位精度，尚未制定多轴机床工作条件下动态精度的测试规范，无法校验多轴机床的加工性能[1]。零件的加工精度受机床静态误差和动态误差两方面的影响，由于缺乏机床动态因素的测试方法，大型关键结构件的加工精度控制成为难点。多轴高速加工与普通数控加工有很大不同，美国佛罗里达大学加工研究中心通过试验发现，高速加工中心中动态因素引起的表面误差(SLE)对工件精度的影响远大于静态几何误差和热误差对工件精度的影响[2]。文献[3-4]研究了高速加工的薄壁件铣削稳定性问题并指出,若加工参数控制不当，加工过程中动力学参数的微小变化就可能产生超过工件容许的误差。

因此，仅研究数控机床的几何精度已经很难满足高速高精度的加工要求。近年来，国内外学者开始致力于建立机床运动机构的动态模型。周勇等[5]研究了具有高速度和高加速度的进给驱动机构动力学行为，根据其动力学特性开发了拥有我国自主知识产权的机床伺服控制方法和数控运动指令。Zhang等[6]建立了高速机床主轴系统动力学模型，通过高速车削中心的性能试验验证了理论建模的正确性。Ding等[7]研究了高速铣削动力学中的稳定性问题，对铣削过程的再生效应进行了深入探讨。上述研究工作为实现机床的动态误差预测奠定了基础。高速高精度机床的动态加工过程是机床机械、伺服、刀具切削等的整体联动过程，为精确描述零件的铣削精度，不仅要考虑静态的机床部件几何误差，而且要对各运动机构的动态行为进行研究，综合分析各因素叠加在机床加工精度上的影响。

1　多轴高速机床完整运动链系统建模

1.1机床加工误差源分析

五轴联动机床的加工误差来源包括几何误差、热变形误差、伺服控制系统误差以及载荷误差四大类[8]，如图1所示。其中,几何精度、定位精度通常是在没有切削载荷、机床不运动或运动速度很低的工况下检测的，一般称为静态精度。静态精度主要取决于机床上的零部件制造与装配精度，如主轴及其轴承、丝杠螺母、齿轮、床身、箱体等，为保证加工出的零件能达到所需的精度，我国对各类通用机床都制订了静态的检测标准，尤其是多轴高速机床，其部件制造和检测标准近乎苛刻，一定程度上保证了机床的有效精度。静态精度只能在有限层面上反映机床的加工精度。在实际工作状态下，还有一些因素会影响工件加工精度，如工作中机床零部件会产生热变形，在切削力作用下机床、工件产生的振动和变形等。在实际切削条件下，在载荷、温升、振动等因素作用下机床精度发生变化，这些因素称为机床的动态因素。研究表明，多轴机床高速铣削时切削力较小，切削时会带走大量的热，高速机床的动态误差主要是切削过程中机械、控制系统的整体联动产生的，机床的基本运动结构以及伺服系统各轴的协调能力与性能是影响机床动态精度的主要因素[9]。

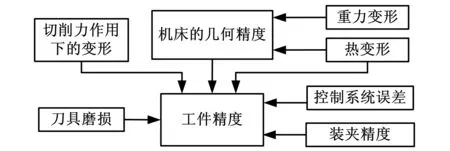
图1　五轴联动数控机床加工误差源

1.2机床机械伺服运动系统建模

图2所示是机床机械、控制系统联动仿真模型，包含位置环节、速度环节、电机环节和机械环节，各基本环节可用传递函数中相应的比例、积分或微分函数表示。对于单轴伺服运动，输入的机床运动指令经位置环节、速度环节、电机环节，最终驱动机械环节。

图2　机床机械、控制系统联动仿真模型

根据零件的数控加工工艺，可计算出各轴运动的位置指令P(X,Y,Z,A,B)，然后由伺服进给系统以这些控制点序列为目标进行随动跟踪控制。运动仿真模型输入各运动轴的理想后置指令，得到实际的输出轨迹，实际轨迹与理想轨迹的轮廓跟踪误差可表示为

(1)

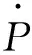
1.3机床加工误差关键动态因素遴选

高速加工中心中由动态因素引起的表面误差对工件精度的影响远大于静态几何误差和热误差，动态误差主要是由切削过程中机械、控制系统的整体联动而产生的，机床的基本运动结构以及伺服系统各轴的协调能力与性能是影响机床动态精度的主要因素。然而，机床动态误差因素众多，如何遴选机床关键影响因素成为误差分析的重要步骤。在图2所示的进给伺服系统仿真模型中改变系统各动态参数，进行阶跃响应测试，对比发现各轴位置环、速度环、加速度对机床伺服系统的动态性能影响较大，图3和图4所示分别为改变位置环比例增益和速度环比例增益后机床动态响应的改变路径。

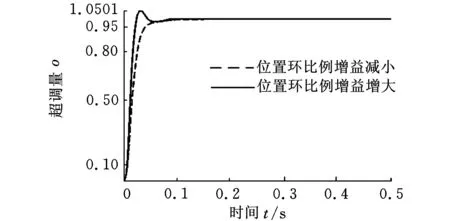
图3　不同位置环比例增益的阶跃响应结果

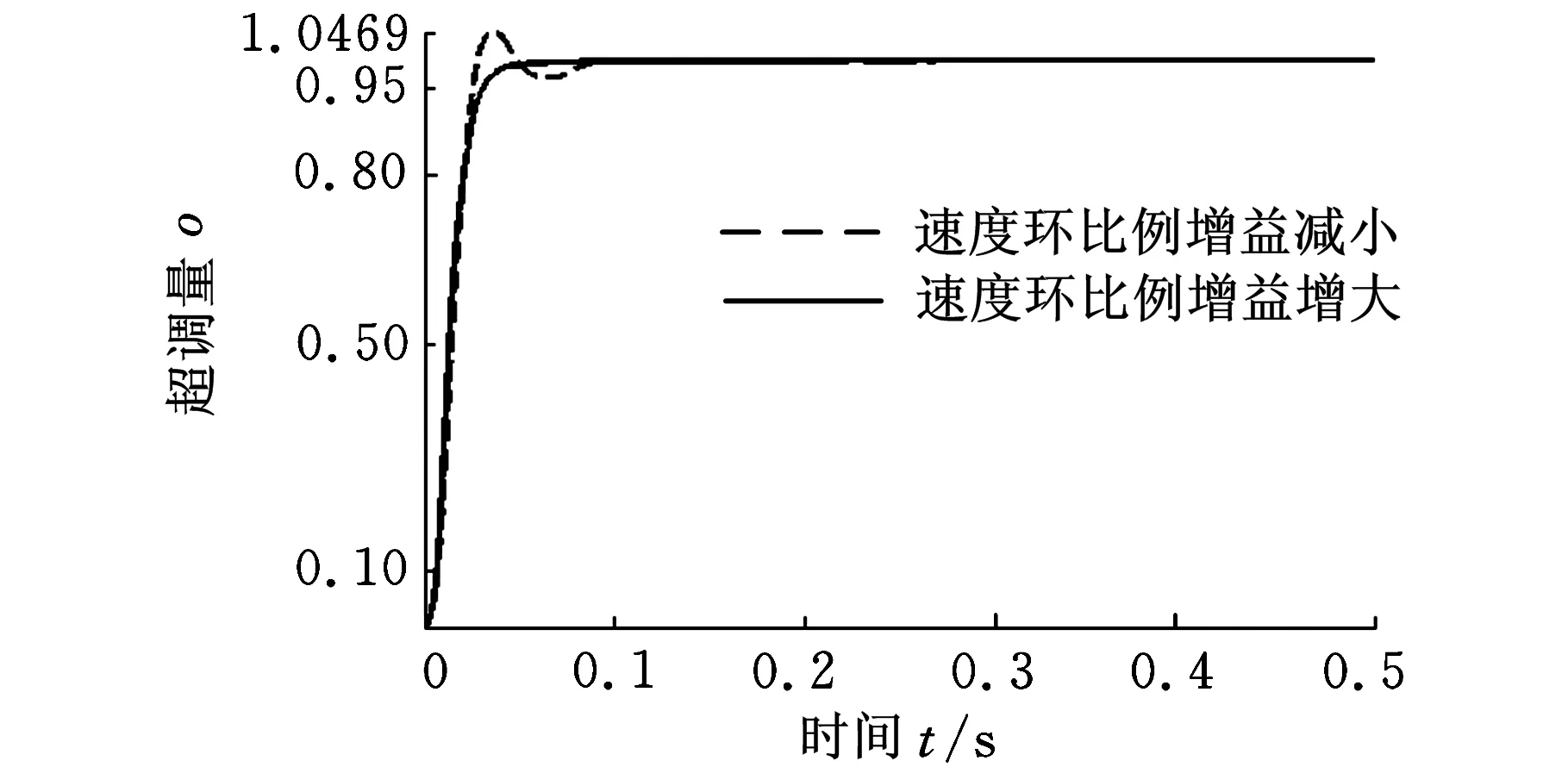
图4　不同速度环比例增益的阶跃响应结果

从图3和图4可以看出：①位置环比例增益决定了进给伺服系统的响应性能，它对进给伺服系统的响应性能有很大的影响。增大位置环比例增益，可以提高系统的响应性，缩短系统的定位时间，有利于减少外部因素干扰的影响，减小系统的稳态误差，提高系统的控制精度。但过高的增益则会导致超调量增大，容易引起零件的过切。②提高速度环比例增益，可以提高进给伺服系统的动态响应速度，有利于提高高速加工中的定位性能，进而提高工件的表面质量和尺寸精度，但速度环比例增益过大，则可能会引起系统振荡；速度环比例增益过小，则可能导致系统的超调量增大。因此，在数控机床驱动机构不产生振动的范围内，速度环比例增益的设定值应越大越好。

2　动静态因素耦合下的零件铣削型面

2.1机床多体运动学模型

数控机床中各运动轴的轨迹、刀具的运动位姿是由实时的各轴轨迹联动构成的，而各轴的实时轨迹是由各运动轴理想轨迹和实际轨迹误差叠加构成的，可依据多体运动学耦合得到。以图5所示的刀具AB两摆机床拓扑结构为例，其建模流程如下。

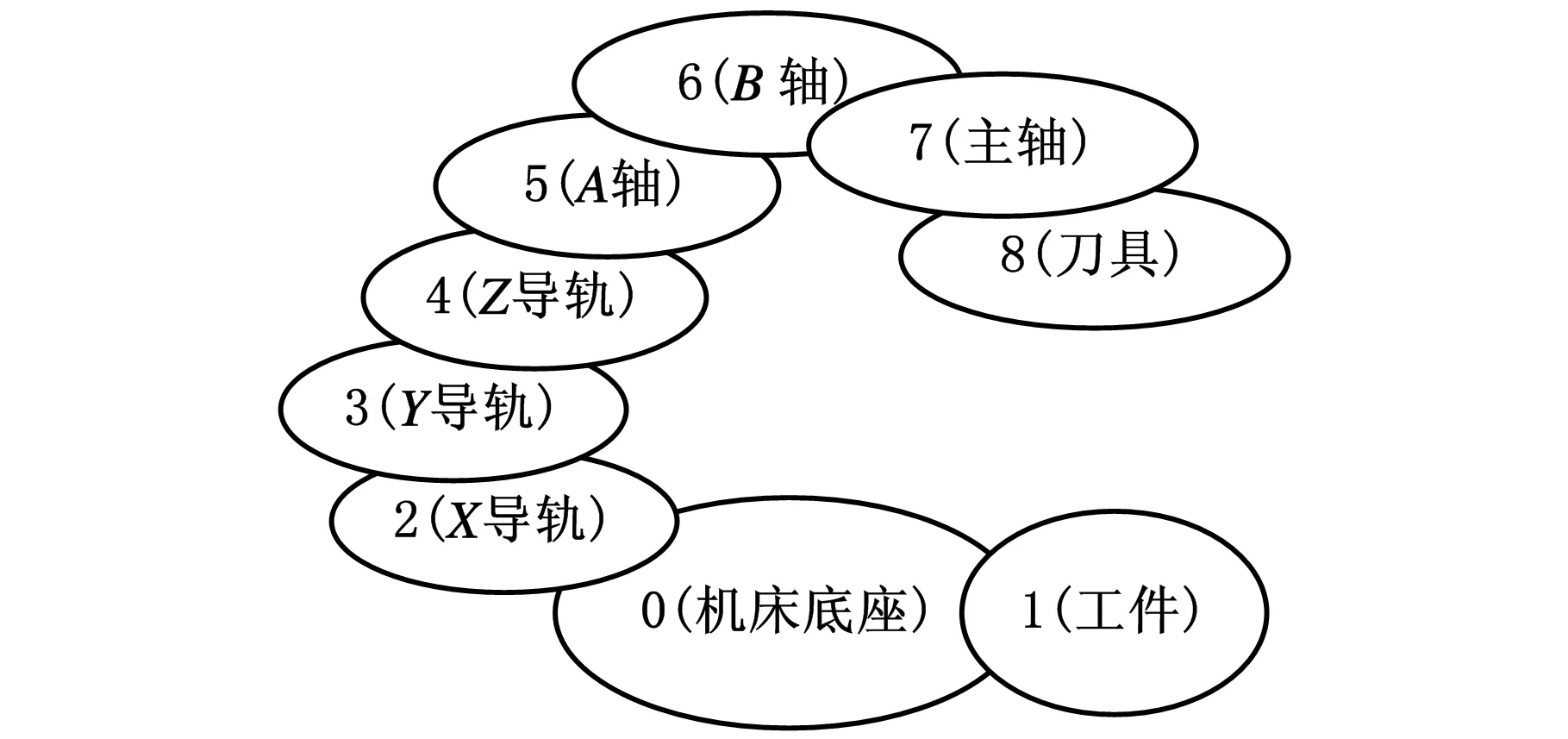
图5　刀具AB两摆机床拓扑结构图

(1)依据多轴数控机床的拓扑结构，用低序列体阵列来描述机床各部件的关联关系。首先设定惯性参考系，设固定不动的工件参考系为B0，远离B0的方向按自然增长数列，依次为各体编号，低序列矩阵可以通过计算得到。任选体Bj为系统中任意典型体，体Bj的n阶低序体的序号定义为

Ln(j)=I

(2)

其中，L为低序体算子，称体Bj为体Bi的n阶高序体，满足下式：

Ln(j)=L(Ln-1(j))

(3)

初始条件为

(4)

根据以上定义，可以计算出机床的各阶低序体阵列。

(2)采用齐次列阵表示各体的位置和矢量姿态。在多体系统中建立广义坐标系，用4×4阶齐次方阵表示相邻两物体间在广义坐标系中的位置坐标和姿态方位的变换。多体系统在理想条件和实际条件下的静止状态、运动状态的体间相对位置和姿态变化可以通过运算该4×4阶齐次方阵来实现，从而完整地描述出刀具的实际运动轨迹以及工件型面切削下的误差分布。

(3)计算刀具体在工件子坐标系中的位置和姿态，完整地推导出刀具在有误差运动机床下的成形约束方程。

刀具成形点的成形函数为

(5)

位置误差为

(6)

姿态误差为

(7)

式中，方阵T为机床相邻部件的体间静止、运动特征矩阵；T(R)为体间静止、运动角误差特征矩阵；Pt为实际加工点在刀具坐标系中的齐次坐标；Pw为理想加工点在工件坐标系中的齐次坐标；Vw为实际加工中刀具姿态矢量在工件坐标系中的齐次坐标；Vt为理想加工中刀具姿态矢量在工件坐标系中的齐次坐标。

2.2零件铣削包络成形点的计算

根据刀具的实际位姿和切削路径构建出切削型面是获取零件铣削型面和加工误差的关键。由于刀具铣削半径的存在，零件型面上的实际成形点位于刀具切削圆的包络线上，因此，还需要基于包络原理求解工件切削型面的实际成形点，实际成形点可以由下式计算得出：

(x-x0)2+(y-y0)2+(z-z0)2=R2

(8)

(x-x0)I+(y-y0)J+(z-z0)K=0

(9)

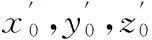
式(8)表示铣削型面的实际成形点在以刀具中心点为圆心的圆上，式(9)表示铣削型面的实际成形点应与刀具切削向量垂直，式(10)表示铣削型面的实际成形点与前后时刻刀具进给移动向量垂直。一般来说，通过联立求解式(8)～式(10)，可以得到内外两个包络点，而在某一时刻，切削零件上只可能有一个成形点，成形点的选取需要借助刀具与工件的实时位置来判断。

2.3铣削成形面的构建

铣削加工时通常沿刀柄的轴线方向设定有固定的铣削层高度，将铣削成形点沿刀柄姿态向量拉伸，可得到铣削层面上的各成形点坐标：

(11)

式中，e_xj、e_yj、e_zj为铣削成形点坐标；h为数据密化的间距；Il、Jl、Kl为刀具实际姿态向量。

在机床动静态误差的作用下，刀具的姿态向量也会发生偏转，应该用实际得到的刀具位姿做数据处理。各个层面的数据相互叠加，最终构成工件的实际铣削型面，最终零件的加工误差可以由理想型面数据与实际型面数据对比而得到。

3　基于S试件的铣削误差分析

3.1五轴机床精加工检验试件——S试件

S试件是航空领域中广泛使用的可用于检测五轴机床加工精度的测试试件[10]，试件采用上下两条扭曲的类S形三阶样条曲线生成直纹面，壁厚为3 mm，可反映五轴数控机床加工的动态特性，由刀具的切削指令和路径构建出S试件的铣削型面是分析机床加工误差影响因素的关键。

图6　S试件

由图6易知，S试件具有变曲率、变开闭角和反向等航空结构件的典型特征，因此具有典型航空件加工过程中的坐标轴指令变化趋势，同时结合各运动轴的运动指令可以获得机床各运动轴的速度、加速度变化情况，以及加工过程中机床不同位置的刚度变化和转换，有利于全面考量机床的运动情况。3.2S试件铣削误差的构建及显示

按照前述铣削型面的构建路线，将S试件理想后置指令输入Simulink仿真模型，改变不同动态误差因素可以获得机床不同状态下各运动轴的实际轨迹，代入机床的多体综合模型可以计算刀具实际的位置和姿态，通过包络理论求解试件的实际铣削成形点，S试件切削层面通过各成形点沿刀具实际姿态向量按照切削深度3 mm拉伸获得，将各层S试件切削型面数据叠加，即为最终的S试件实际型面，如图7所示，试件型面上用颜色区分不同的误差大小，可以形象表示出S试件切削型面上的误差分布。

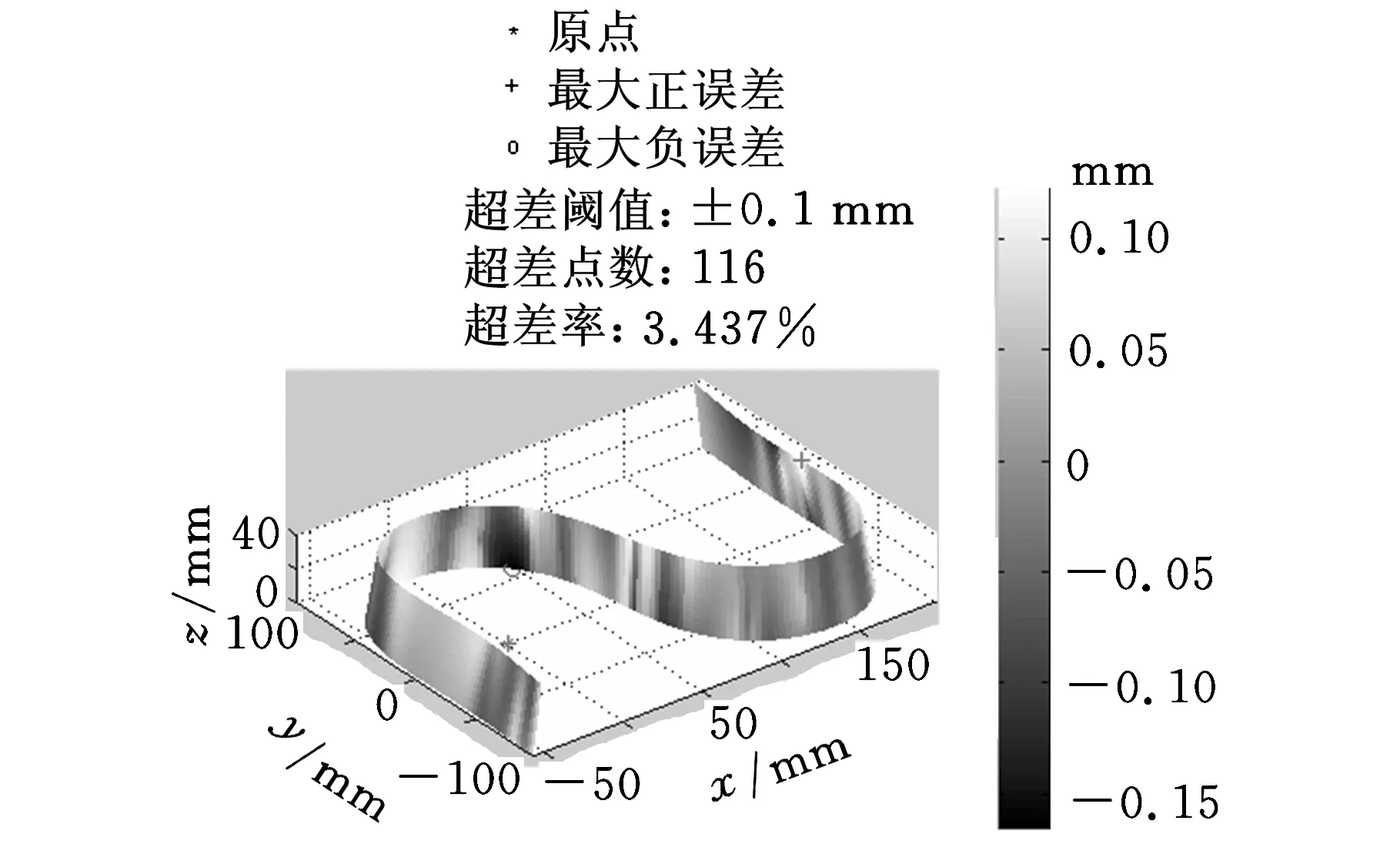
图7　S试件铣削误差型面数据

4.3机床动静态因素与S试件型面误差的映射关系

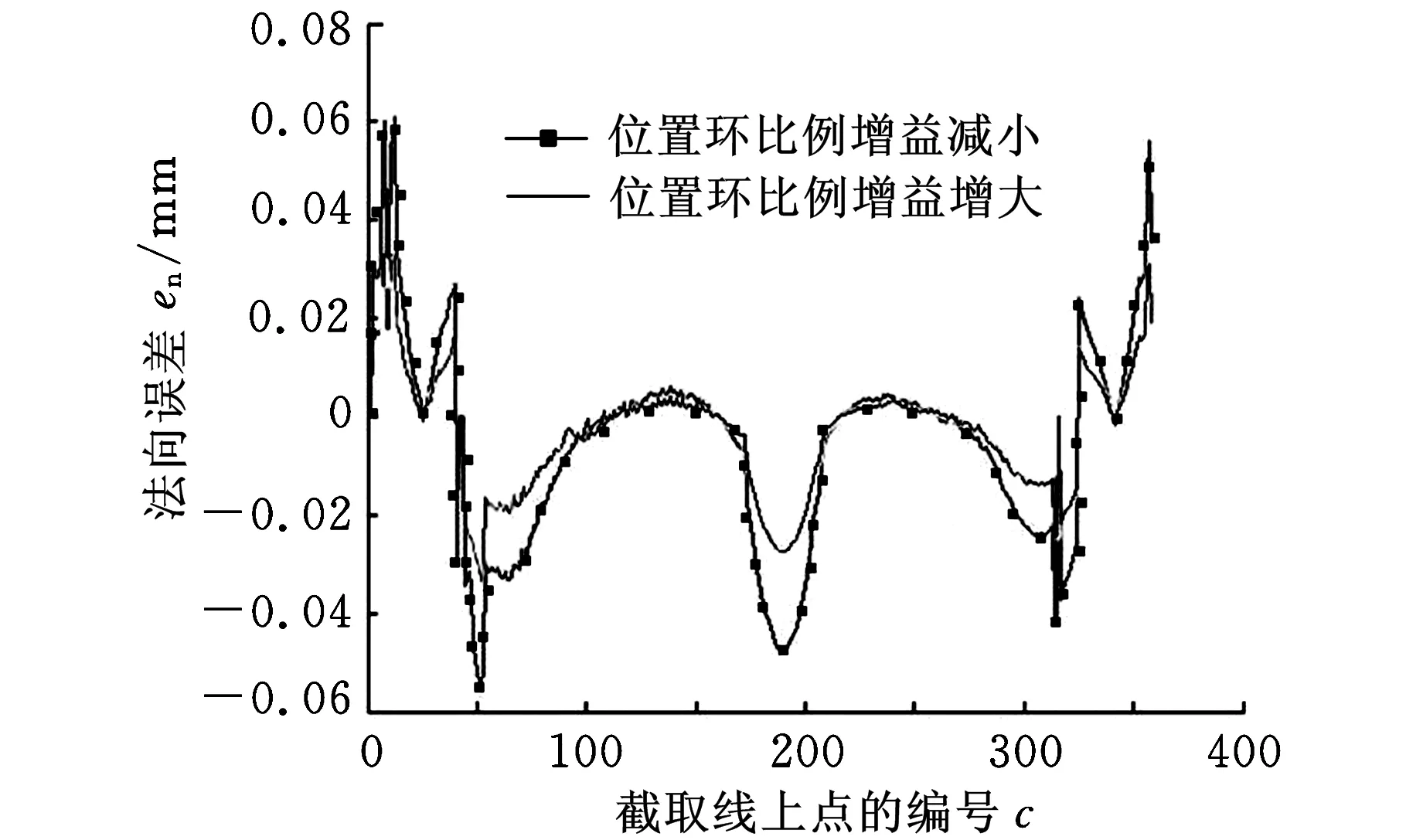
(a)位置环增益变化

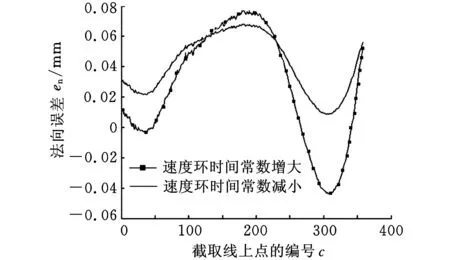
(b)速度环时间常数变化图8　S试件型面误差分布

为便于描述S型面的误差分布，在不同高度上作S试件的平面截取线，依据仿真平台，提取分析各层截取线上点的法向误差分布。图8所示为改变机床动态因素中的X轴位置环增益和B轴速度环时间常数，得到的S试件在高度22.5 mm处截取线的法向误差分布规律，图中横坐标为截取线上成形点的编号，纵坐标为该点下的法向误差值。由图8可知，位置环增益、速度环时间常数的变动体现为型面法向误差的整体变化，其中位置环增益与S截线的法向误差成负相关关系，即位置环增益变大导致S试件型面误差变小；而速度环时间常数变大则型面误差变大，二者基本成正相关关系。

4.4基于正交实验设计的S试件误差预测结果校验

为进一步验证误差综合预测平台结果的正确性，以及X、A轴位置环增益，Y、B轴速度环时间常数，X、A轴加速度及轴间异面误差共7个动态因素对加工精度的影响，进行了S试件切削实验，切削后的S型面使用三坐标机测量误差分布。

4.4.1S试件切削方案设计

由于动态因素众多，如果对7个因素逐一进行水平变化实验，假定每个因素的水平变化为2个，则至少有27=128次试件切削。为此，基于正交实验理论设计切削实验，通过标准正交实验表安排实验，对7个因素同时变化开展实验，只需做8次实验。本实验采用的是某国产五轴联动数控铣床，毛胚材料为铝合金，型号为7075-T7451，精加工刀具为右旋棒铣刀，刀具直径为20 mm，采用分层侧铣加工方法，沿刀具轴线方向自上而下按每层3 mm进行精加工铣削。根据正交实验表，改变位置环增益等相关动态因素的水平值，共进行8次实验，最终得到8个S试件，如图9所示。实验结束后，利用三坐标测量机测得S试件在高度22.5 mm处截取线数据点的法向误差。

4.4.2实验结果分析

按照正交实验设计所得到的实验结果，使用SPSS统计学软件做专门的回归分析，建立多元的输入(机床各动态因素指标)和输出(S型面各点法向误差值)之间的关联关系：

yi=β0+β1xi1+β2xi2+…+βnxin+εi

(12)

式中，yi为指标观测值；β0,β1,…,βn为线性回归系数，是回归分析的主要内容，通过最小二乘法估计得到；xin为第i次实验考查的n个可控自变量；εi为实验过程中的随机误差。

分析各实验因素单独、耦合变动时对应S型面法向误差的定性规律。同时通过线性回归系数可以得到各实验因素对S型面法向误差影响的权重。

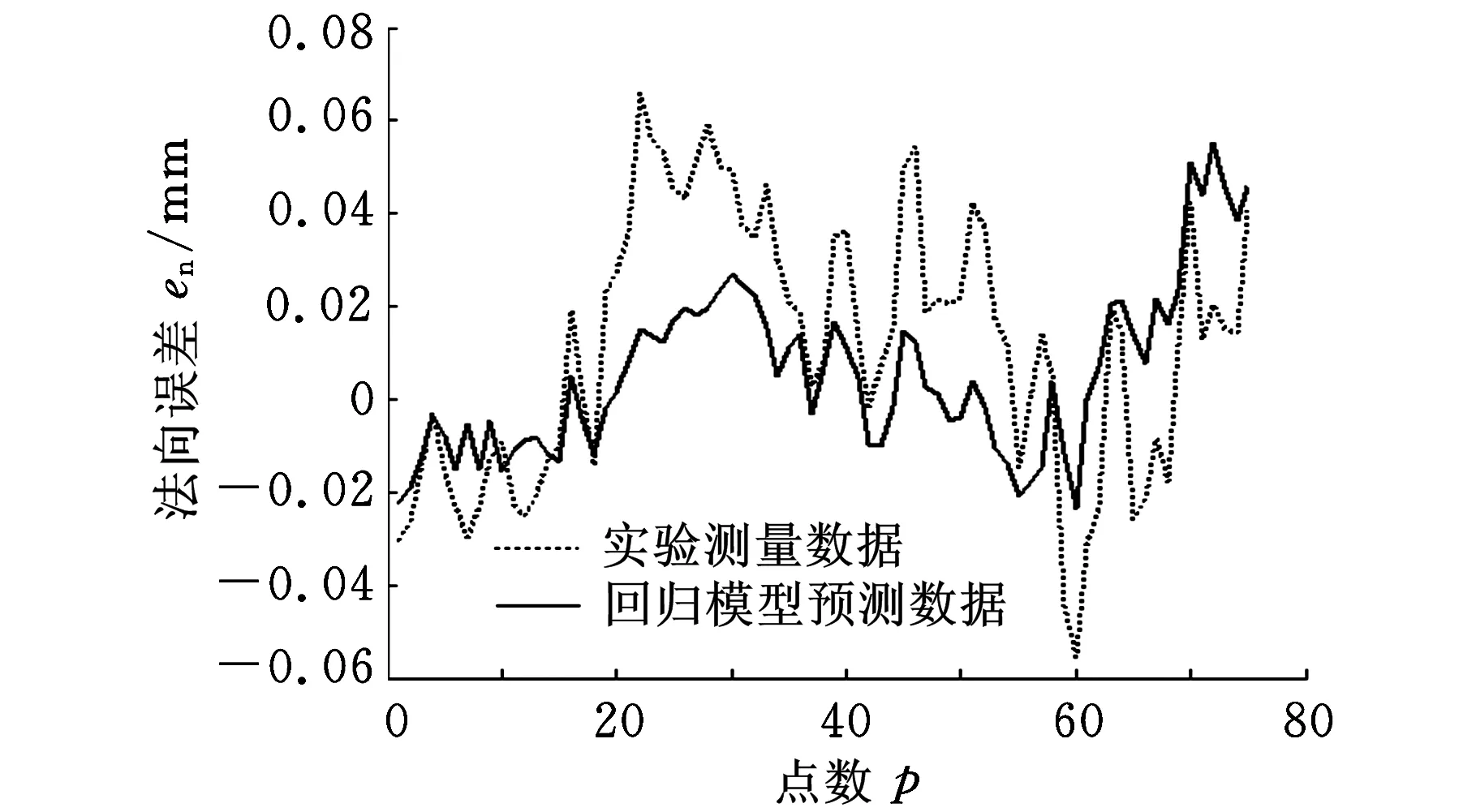
图10　实测数据与预测数据对比

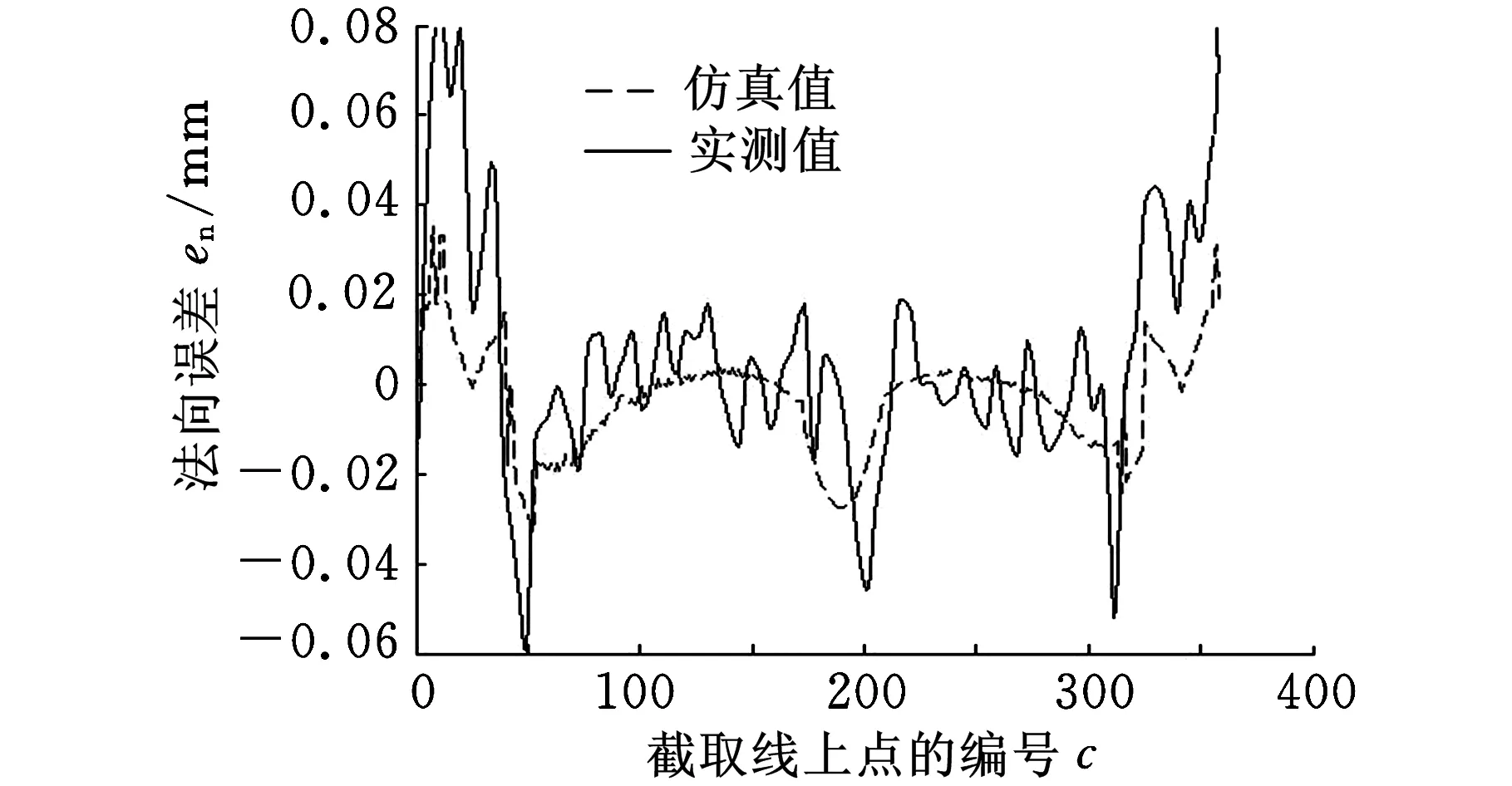
(a)位置增益变大

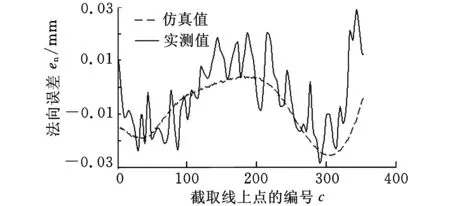
(b)速度环时间常数变小图11　实验与仿真结果对比

图10是回归分析预测模型与实验测量数据的对比分析图，测量数据与回归模型在量程和趋势上都保持一致，具有较高的吻合度。基于回归方程，可以进一步分析单个动态因素对试件法向误差的影响，剥离出单一因素影响下试件法向误差测量值。图11所示分别为位置环增益和速度环时间常数两个因素独立影响下S试件法向误差分布情况，可见仿真预测平台给出的误差分析结果与实测数据保持了较高的重合度，验证了该仿真平台的准确性。从图11中可以看到，实际测量误差值大于仿真误差，这可能是因为仿真平台未考虑机床热变形等其他因素的影响，机床在实际加工过程中还受到其他未知因素的影响，因而导致S试件的实测误差值偏大。

5　基于误差数据库的神经网络误差辨识技术

5.1神经网络误差辨识模型

基于仿真预测平台得到的机床加工误差因素数据库，可以利用神经网络训练技术，完成对机床加工后的状态预测。以S试件加工误差分布为例，首先建立每一个动态因素变动时对应的法向误差向量Ei=(ai1,ai2,…,ain)(Ei表示第i个动态因素对应的误差矩阵，n表示误差矩阵中包含的误差值个数)。然后，基于误差矩阵与动态因素之间一一对应的映射关系，将实验切削误差向量X=(x1,x2,…,xn)代入下式计算出X对于Ei的隶属度：

μ(x)=e-k(x-a)2k>0

(13)

其中，a为Ei中的误差值；x为给定误差矩阵X中的误差值。将计算出的隶属度μX=(μ1,μ2,…,μn)代入绝对海明公式中计算出对应的贴近度值，按照贴近度最大原则，最终溯源出影响机床性能的主要动态因素。关于E、X的贴近度值为

(14)

μE(xi)=1

基于MATLAB建立图12所示的3层BP神经网络辨识模型，输入是S型面的若干点位，输出是机床精度指标。通过神经网络代入样本进行训练，训练过程不断调整三层之间连接的权值和阈值，从而实现S型面点的法向误差和机床精度指标大小的映射关系。模型训练完毕后，用实例的S试件型面各点法向误差作为新的输入，经网络迭代辨识产生相应的机床精度指标量值。BP网络的传递函数有多种，如Logsig型传递函数、tansig型传递函数以及purelin型传递函数等。经过反复尝试对比，选用tansig型传递函数得到的误差最小。

图12　3层BP神经网络辨识模型

5.2误差辨识算例

利用型号为V5-1030-ABJ的某国产五轴数控铣床进行S试件切削实验，运用三坐标测量机测量出切削后的S试件法向误差，共测量了75个点的法向误差值。

将S试件切削后误差输入所建立的仿真误差辨识模型中，误差数据库中共考虑了17个机床关键因素，每个因素考虑两种工况，因此映射数据库中包含34组S试件法向误差。从数据库中分别提取位置增益、B轴加速度、X轴加加速度所对应的S试件法向误差进行BP神经网络的训练样本，最终输出的机床误差因素结果见表1，可辨识出影响该S试件加工误差的三个主要因素和所占比例。

表1　误差影响因素辨识结果

6　结语

复杂曲面结构变化多样，使得主轴数控机床铣削加工中，对其精度的控制成为难点，铣削过程中机床微小的因素变化都可能导致零件的误差超过允许误差。本文通过研究五轴机床加工主要误差源，提出耦合机床动静因素构建零件实际铣削型面的方法，由各运动轴伺服运动模型和多体运动模型构建机床完整的运动链系统模型，由包络理论求解零件的铣削成形点、线和层面，最终获得零件的铣削精度。以航空S试件为例，给出了S试件加工精度和机床动静态因素的映射关系，并在切削实验中予以验证。该平台可以实现航空结构件铣削精度的预估，根据计算结果可用于评估机床的加工状态，从而为机床复杂的因素调整提供了科学依据；与此同时，获取机床动静态因素和型面铣削精度映射关系后，可根据现有零件的误差分布研究辨识出机床影响因素的方法，因而具有更好的精度控制效果和科学的指导意义。

[1]LinRS,HuCW.ModelingoftheDynamicContourErrorofFive-axisCNCMachineTools[J].ASMEDynamicSystemsControlandControlDivision, 1999, 67:861-868.

[2]SchmitzTL,ZiegertJC,ZapataR.PartAccuracyinHigh-speedMachining:PreliminaryResults[C]//ProceedingofMESC2006.Ypsilanti, 2006.

[3]SongQH,WanY,AiX,etal.NovelMethodforDynamicOptimizationofStabilityinHigh-speedMillingSystem[J].TransactionsofNanjingUniversityofAeronautics&Astronautics,2009,26(3):184-191.

[4]汤爱君, 刘战强. 铣刀参数对薄壁零件铣削稳定性的影响[J].华南理工大学学报(自然科学版),2009,37(2): 29-34.

TangAijun,LiuZhanqiang.EffectofMillingCutterParametersonMillingStabilityofThin-wallParts[J].JournalofSouthChinaUniversityofTechnology(NaturalScienceEdition), 2009,37(2): 29-34.

[5]周勇, 陈吉红, 彭芳瑜. 高速高精度数控进给驱动的机电联合系统仿真[J].机械科学与技术, 2007, 26(2): 135-139.

ZhouYong,ChenJihong,PengFangyu.MechatronicIntegratedSystemSimulationforaHigh-speedandHigh-precisionCNCFeedDrive[J].MechanicalScienceandTechnology, 2007, 26(2): 135-139.

[6]ZhangYM,LinXL,WangXD,etal.TheStudyontheDynamicCharacteristicofHighSpeedMachineToolandExperimentValidate[J].MaterialScienceForum,2004, 471/472：765-769.

[7]DingYe,ZhuLimin,ZhangXiaojian,etal.NumericalIntegrationMethodforPredictionofMillingStability[J].JournalofManufacturingScienceandEngineeringTransactionsoftheASME, 2011, 133(3):31-40.

[8]TranHD,SuJC,ClaudetAA.QuantificationofUncertaintyinMachiningOperationsforOn-machineAcceptance[R].Albuquerque：SandiaNationalLaboratories, 2008.

[9]MasaomiT,DaisukeY,KeizoU,etal.EvaluationofSynchronousMotioninFive-axisMachiningCenterswithaTiltingRotaryTable[J].JournalofAdvancedMechanicalDesign,SystemsandManufacturing, 2007, 1(1):24-35.

[10]CuiYawen,SongZhiyong.S-shapeDetectionTestPieceandaDetectionMethodforDetectionthePrecisionoftheNumericalControlMillingMachine：US，8061052B2[P]2011-11-22.

(编辑陈勇)

Prediction on Machining Accuracy of Five-axis Milling Tool for Multiple Error Source Coupling

Wang Wei1,2Zheng Congzhi1Zhang Xin3

1.University of Electronic Science and Technology of China,Chengdu,611731 2.AVIC Chengdu Aircraft Industrial(Group) Co., Ltd.，Chengdu，610092 3.No.30 Institute of China Electronic Technology Corporation,Chengdu,610041

A method integrated with dynamic error factors and static geometric errors was presented to build the surface data of actual workpiece. Each servo axis movement was simulated and composed by kinematics of the joint bodies of the machine for calculating the actual position and attitude of the tool. The actual milling point was solved by the envelope theory and the final part of the surface was obtained by the surface forming method. A case study was analyzed through the S specimen sample, which was verified the composition of surface methods and get the milling errors caused by influences of dynamic factors, such as the gap, the position loop and speed loop.The results were verified by experimental data through regression analysis. Finally, the error track model was established based on neural network for condition assesment after machining. The developed platform may provide technical support for the realization on precision forecasting and security for large-scale and the key structure.

dynamic error; precision modeling; accuracy prediction; aerospace monolithic component; multi-axis CNC machine

2013-09-12

国家自然科学基金资助项目(51205048)；中央高校基本科研业务费专项资金资助项目(ZYGX2011J082)

TH161.5DOI：10.3969/j.issn.1004-132X.2015.01.015

王伟，男，1980年生。电子科技大学机械电子工程学院副教授、博士，成都飞机工业(集团)有限责任公司博士后研究人员。主要研究方向为精密制造及精密检测、机械系统动力学。发表论文20余篇。郑从志，男，1988年生。电子科技大学机械电子工程学院硕士研究生。张信，男，1988年生。中国电子科技集团第三十研究所助理工程师。