三维斜流线性完全耦合层吸收边界条件

伍　新　陈志夫　尹汉锋

1.湖南大学汽车车身先进设计制造国家重点实验室，长沙，4100822.湖南工程学院，湘潭，4111043.广州汽车集团股份有限公司汽车工程研究院，广州，511434

三维斜流线性完全耦合层吸收边界条件

伍新1,2陈志夫3尹汉锋1

1.湖南大学汽车车身先进设计制造国家重点实验室，长沙，4100822.湖南工程学院，湘潭，4111043.广州汽车集团股份有限公司汽车工程研究院，广州，511434

采用傅里叶与拉普拉斯变换方法分析了三维斜流背景下声波、涡波与熵波的色散关系；根据各物理波的色散轨迹特征，结合频率变化的时空坐标变换方法，给出了一组时间与空间坐标变换关系式，并将三维斜流线性欧拉方程变换至新坐标系；采用复数变换方法，引入阻尼，分别构建了x层、y层、z层及角层的完全耦合层(PML)吸收边界条件,给出了吸收项的施加原则；最后通过三维脉冲声波、对称涡环与周期性点声源在斜时均流中的传播问题验证了该吸收边界条件的正确性。研究结果表明：所提出的坐标变换关系能够有效解决各物理波相位速度与群速度不一致的问题；在斜背景流下，该PML吸收边界条件能较好地吸收物理波，有效抑制边界反射，可用于气动声学计算。

完全耦合层；边界条件；计算气动声学；欧拉方程；色散

0　引言

在开放区域气动声学问题的数值计算中，无限计算域需要人工截断，形成一种特殊的边界条件，即无反射边界条件，它既要使计算域内的各种物理波能无反射或者较小反射地通过边界，又能让计算域外的物理波能顺利通过边界进入计算域，同时，还能阻止计算域外的非物理波传入计算域。完全耦合层(perfectly matched layer,PML)吸收边界条件作为最优秀的无反射边界条件之一，在近年取得了极大的发展。

文献[1-5]首次将Berenger提出的PML技术引入计算气动声学领域，提出了一系列稳定的PML吸收边界条件。Lin等[6]建立了一个适用于平行流计算的非线性和黏性PML吸收边界条件。结合谱差分方法，Zhou等[7]采用该黏性PML吸收边界条件求解了圆柱绕流等典型气动声学问题。柳占新等[8]从声学角度推导了笛卡儿坐标系和柱坐标下全欧拉方程的PML吸收边界条件，并将其应用于涡扇发动机进气道流场模拟。周正干等[9]应用PML技术分析了超声波声场特性。Parrish等[10-11]通过两次坐标变换，提出了稳定的二维线性和非线性斜流PML吸收边界条件，并将其拓展至圆柱坐标系。虽然上述PML吸收边界条件具有较高的数值精度，但是，它们无法求解三维任意方向入流问题。

在汽车侧风、圆柱或钝体斜向绕流等气动声学问题的数值计算中，往往存在背景斜流。斜流使流场内各物理波的群速度与相位速度方向不同，这给稳定的PML构造带来了挑战，即如何建立正确的坐标转换关系[12]。针对该问题，本文从控制方程内各物理波的色散关系轨迹出发，构建恰当的坐标转换关系，修正各物理波的群速度与相位速度方向，发展三维斜流线性PML吸收边界条件。

1　控制方程色散关系分析与坐标变换

1.1控制方程

笛卡儿坐标系下，三维量纲一斜流线性欧拉方程为

(1)

其中，ρ为密度，u、v、w分别为x、y、z方向的速度，Max、May、Maz分别为x、y、z方向的马赫数，p为压力，H为非定常源项。

1.2色散关系分析

根据波数分析理论，对式(1)等号两边进行傅里叶与拉普拉斯变换：

(2)

其中，ω为频率，kx、ky、kz分别为x、y、z方向的波数。经该变换后即可获得三维斜流线性欧拉方程的色散关系矩阵Ψ：

(3)

λ=ω-Maxkx-Mayky-Mazkz

通过求解色散关系矩阵Ψ的零点λi(i=1,2,…,5)即可获得各物理波的色散关系。熵波与涡波的色散关系为

ω-Maxkx-Mayky-Mazkz=0

(4)

声波的色散关系为

(5)

为了分析各物理波的群速度与相位速度方向，将式(4)与式(5)等号两边同时除以频率ω，得

(6)

(7)

涡波、熵波及声波在坐标系(kx/ω,ky/ω,kz/ω)内的色散关系轨迹如图1a所示。图1a中，涡波与熵波的色散关系轨迹为一个斜置的平面，声波的色散关系轨迹为一个中心不在坐标系原点的斜置椭球。根据色散关系轨迹稳定性分析方法[13]，三维斜流线性欧拉方程中，不论是涡波、熵波还是声波，其色散关系轨迹均存在不稳定区域，因此，在进行PML变换之前，必须采用适当的坐标变换来修正域内各物理波的群速度与相位速度方向。

1.3坐标变换关系的构建

如果将z方向的斜流消去，则该问题可以转化为二维斜流线性欧拉方程的坐标变换关系式的推导。参考文献[13]中的结论，x层坐标变换的关系式可以表示为

(8)

式中，t为时间。

由式(8)可获得各物理量关于新坐标与原坐标偏导数之间的关系:

(9)

与式(9)相对应的新波数、新频率与原波数、原频率之间的关系为

(10)

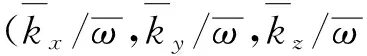
(11)

声波的色散关系为

(12)

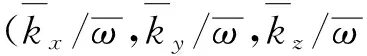
同理，可以获得用于y层与z层PML吸收边界条件推导的坐标变换关系式，其表达式分别为

(13)

(14)

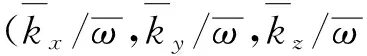
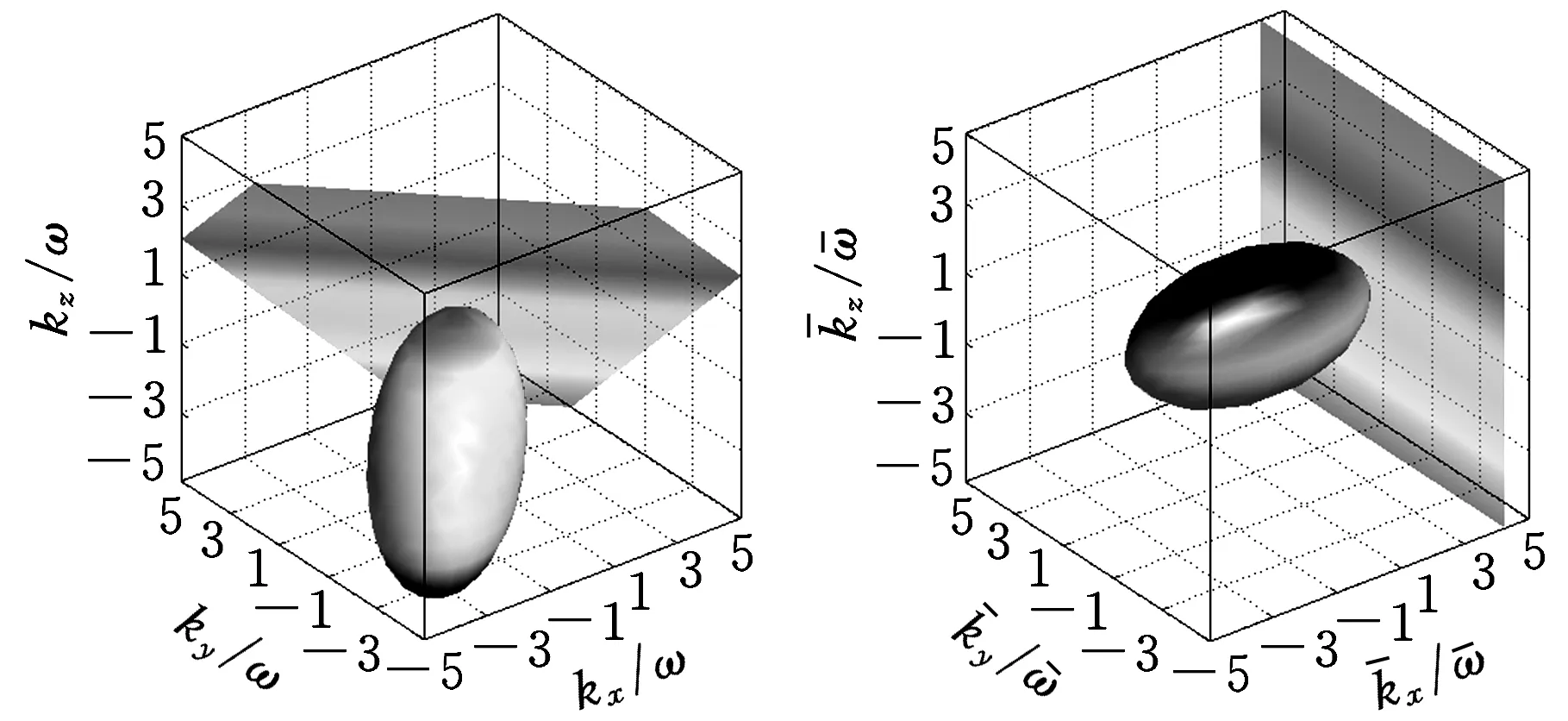
(a)变换前(b)x层

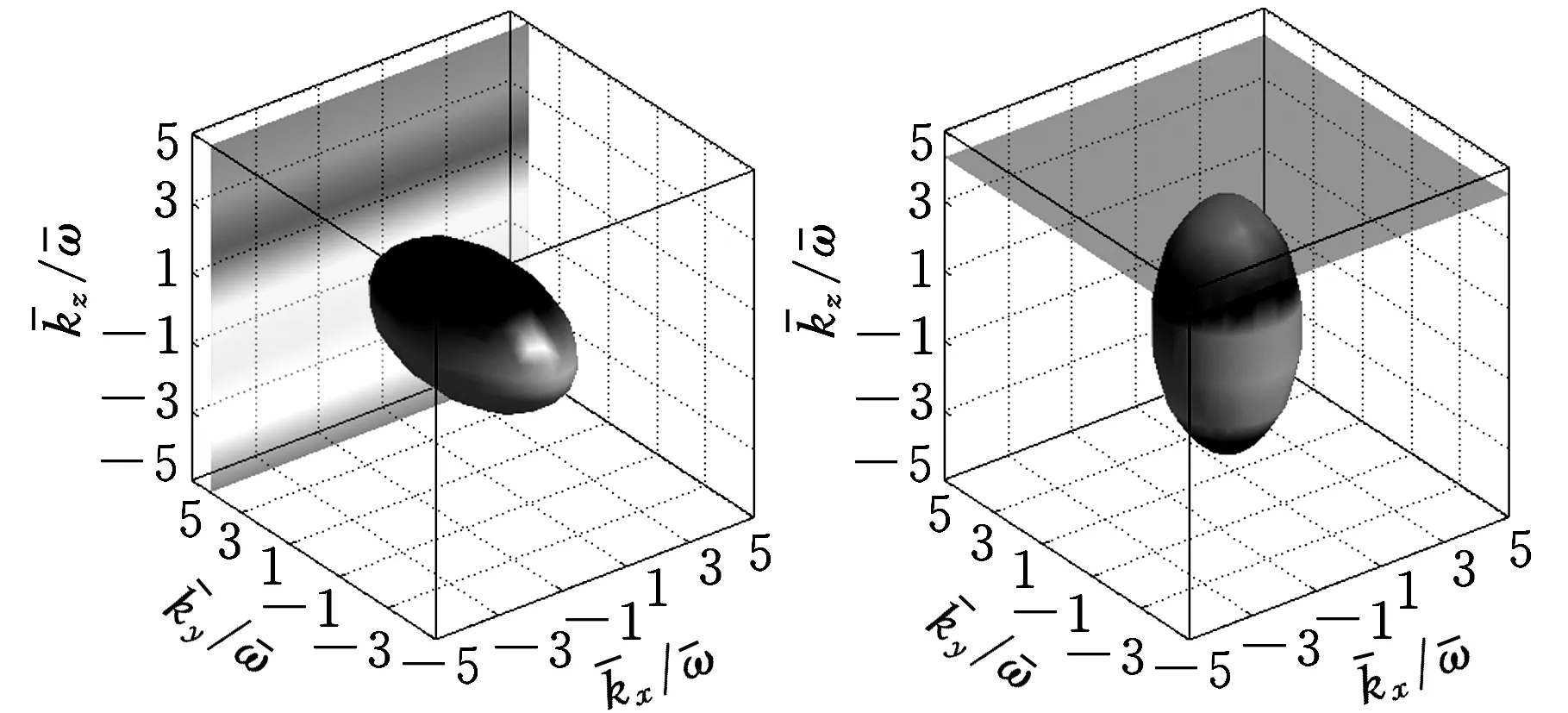
(c)y层(d)z层图1　物理波在坐标系(kx/ω,ky/ω,kz/ω)与内的色散关系轨迹

2　PML吸收边界条件推导

采用复数变换方法，通过式(8)、式(13)与式(14)分别推导x层、y层及z层的PML吸收边界条件。然后，根据各层PML吸收边界条件推导各角层PML吸收边界条件。对于三维计算域，整个计算域由26块PML吸收域与一个物理计算域组成，PML吸收边界条件由七大部分组成，分别为x层、y层、z层、xy层、yz层、xz层及xyz层，如图2所示。

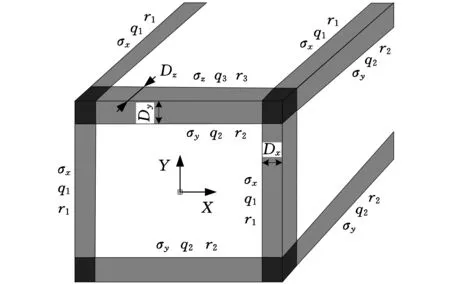
图2　物理域与PML计算域示意图

2.1平行层PML吸收边界条件

首先，将式(9)代入式(1)，将控制方程变换至新坐标系：

(15)

其次，引入阻尼，将新时间、空间坐标系下的控制方程转换至频域：

(16)

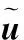
再次，引入辅助变量q1，将频域PML吸收边界条件变换至新的时间与空间坐标系：

(17)

(18)

最后，通过式(9)将新时间、空间坐标系下的PML吸收边界条件变回至原时间与空间坐标系，获得x层PML吸收边界条件：

(19)

(20)

同理，也可获得y层与z层PML吸收边界条件：

(21)

(22)

(23)

(24)

2.2角层PML吸收边界条件

关于xy层PML吸收边界条件，吸收系数σx与σy均不为零，因此结合x层和y层PML吸收边界条件即可得xy层PML吸收边界条件，其表达式为

(25)

(26)

(27)

为了使xy层PML吸收边界条件稳定，在辅助变量方程(式(26)与式(27))等号左边，分别增加额外的吸收项σyq1与σxq2，该吸收项对稳定性的影响详见文献[13]。

同理，也可获得yz层和xz层PML吸收边界条件，其表达式分别为

(28)

(29)

(30)

(31)

(32)

(33)

为使各角层PML吸收边界条件稳定，在式(29)、式(30)、式(32)与式(33)等号的左边依次增加吸收项σzq2、σyq3、σzq1与σxq3。

关于xyz层PML吸收边界条件，吸收系数σx、σy与σz均不为零，因此必须结合x层、y层和z层PML吸收边界条件即可得xyz层PML吸收边界条件，其表达式为

[σx(I+βxA)+σy(I+βyB)+σz(I+βzC)]u=0

(34)

(35)

(36)

(37)

式(35)～式(37)中，(σy+σz)q1、(σx+σz)q2与(σx+σy)q3分别为辅助变量方程中额外增加的吸收项。

3　算例验证

为验证本文构建的三维斜流线性PML吸收边界条件的正确性，选用三维脉冲声波、对称涡环与周期性点声源在斜时均流中的传播问题作为测试算例。计算域四周均采用PML吸收边界条件，空间离散格式采用改进的7点色散保持有限差分格式[13]，时间推进格式采用6级4阶低耗散低色散RK显式格式[14]。为了消除短波对数值计算的影响，采用人工黏性耗散[15]进行计算。计算时空间网格尺寸Δx=Δy=Δz=1，时间步长取0.1 s，吸收系数σx、σy、σz分别为

(38)

D为PML吸收宽度，xb、yb、zb分别为PML计算域与欧拉计算域的交界位置，根据文献[10]，σm、α分别取值2、3。

3.1脉冲声波传播

假定该脉冲声波初始位置在坐标原点，并且处于速度场为(0.5,0.5,0.5)的时均流场中，该问题的初始条件可描述为

(39)

设该问题的欧拉计算域为x,y,z∈[-20,20]，吸收宽度取值为D=10Δx=10Δy=10Δz，在t=40 s时的压力等值面及截面等值线如图3所示。可以看出，当三维脉冲声波达到PML吸收边界时，声波迅速衰减，在边界处未见明显反射。

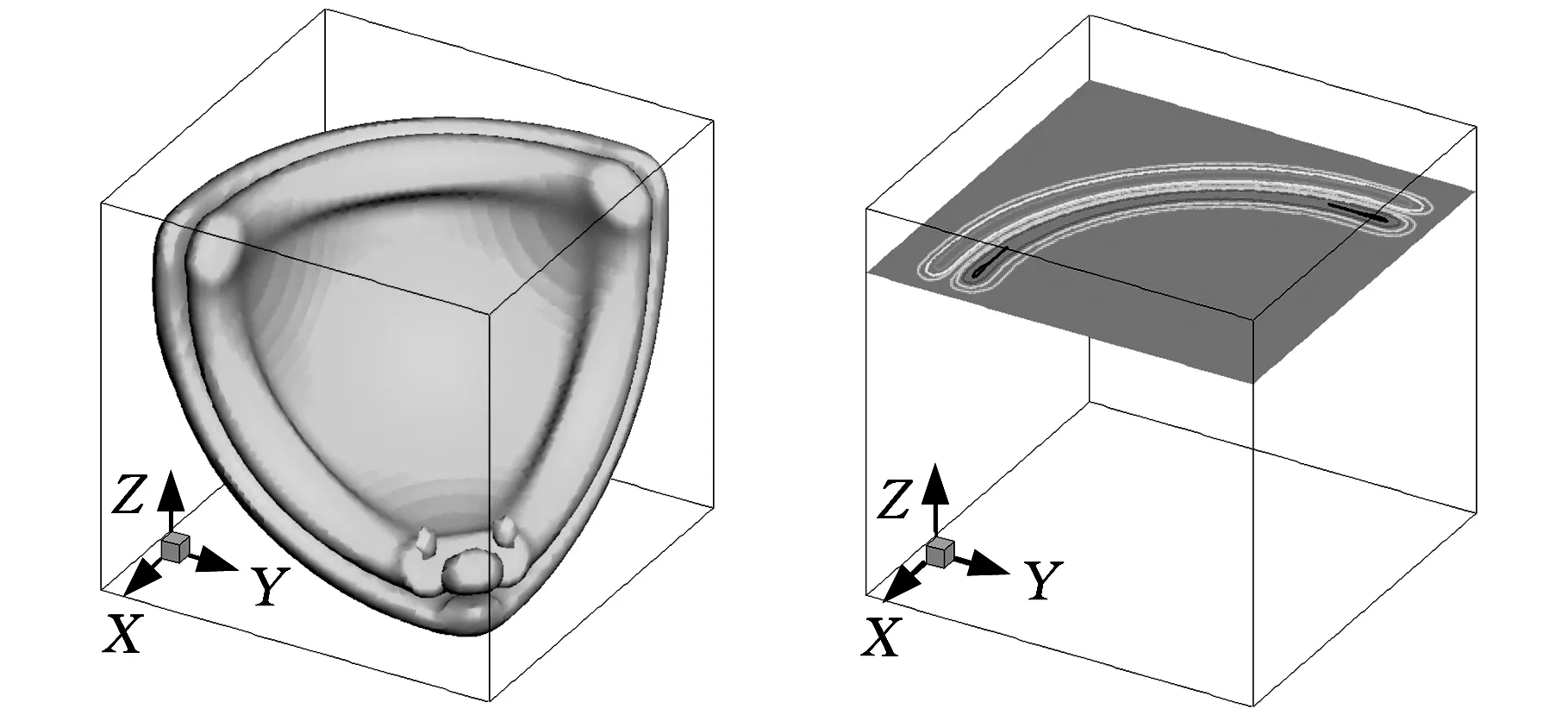
(a)压力等值面图(b)平面z=20上的压力等值线图图3　t=40 s时压力图

3.2涡环传播

涡环动力学及其发声机理是目前一个非常活跃的研究方向，也是理论流体力学与气动声学领域中的难点。以对称涡环在斜时均流中的传播问题作为测试算例进行测试。设涡环的半径r0=10，涡核的半径b=3，初始时刻涡环对称中心位于坐标系原点，将该涡环置于(0.5,0.5,0.5)的时均流场中，如图4所示，该问题的初始条件可描述为

(40)

ux(r)=εr0r-1(r-r0)e-α[x2+(r-r0)2]

ur(r)=-εr0r-1(r-r0)xe-α[x2+(r-r0)2]

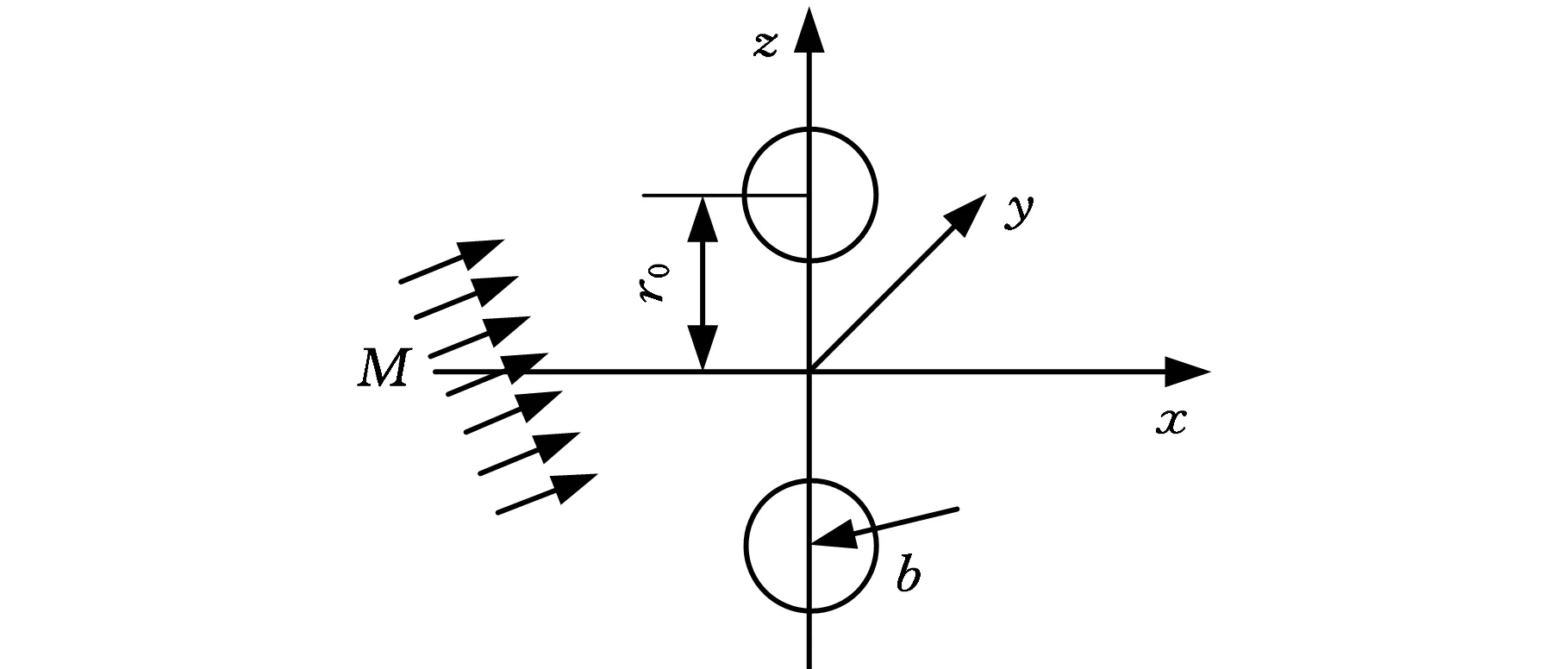
图4　对称涡环示意图

采用与3.1节中相同的计算方案，获得涡量随时间的变化情况，如图5所示。该涡环随时均流对流，可以看出，当涡环到达PML计算域内时，涡量迅速衰减，且未见明显反射。由此可知，当任意方向斜流存在时，涡环能顺利穿过计算边界，该PML吸收边界条件能较好地吸收涡环中的物理波。

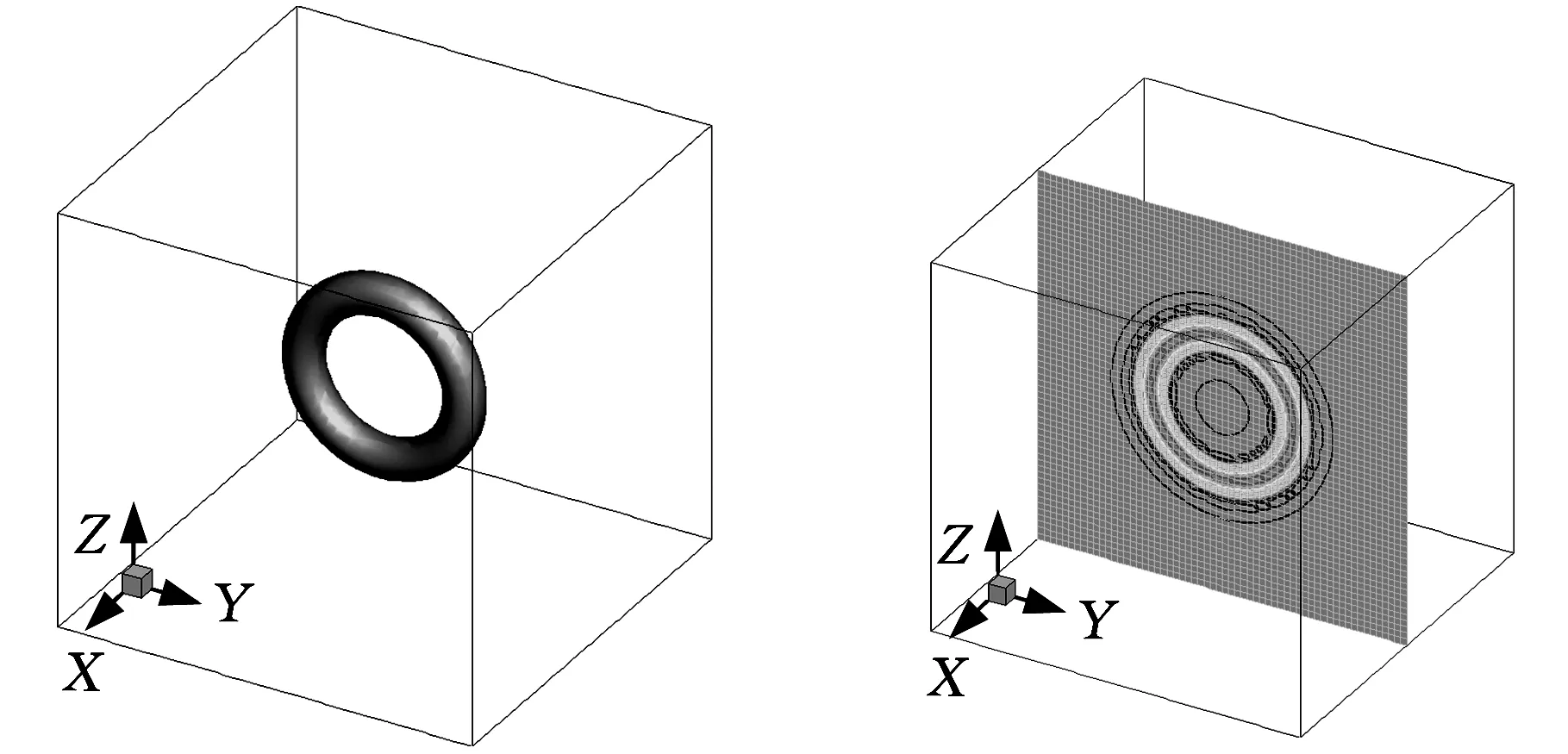
(a)t=0时涡量等值面图(b)t=0时平面x=0上的涡量等值线图

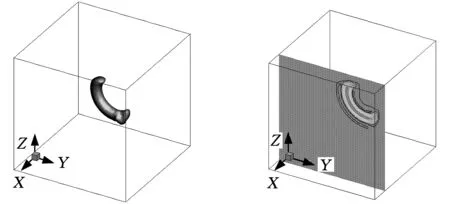
(c)t=40 s时涡量等值面图(d)t=40 s时平面x=20上的涡量等值线图图5　涡量随时间变化图

3.3周期性点声源传播

为了测试PML吸收边界条件对周期性声波的吸收性能，在式(1)中的压力方程右端施加一个周期性点声源，该点声源为

s(x,y,z,t)=sin(0.2πt)e-(ln2)[x2+y2+z2]/32

(41)

欧拉计算域为x,y,z∈[-40,40]，计算域外围采用10层PML吸收边界条件。

当t=100s时，压力数值解等值面与等值线如图6所示。可以看出，周期性声波能无反射地通过边界。

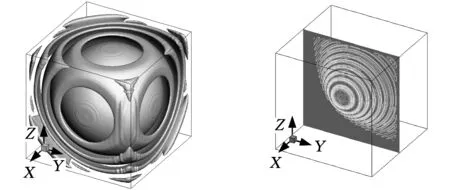
(a)声压等值面图(b)平面x=0上的声压等值线图

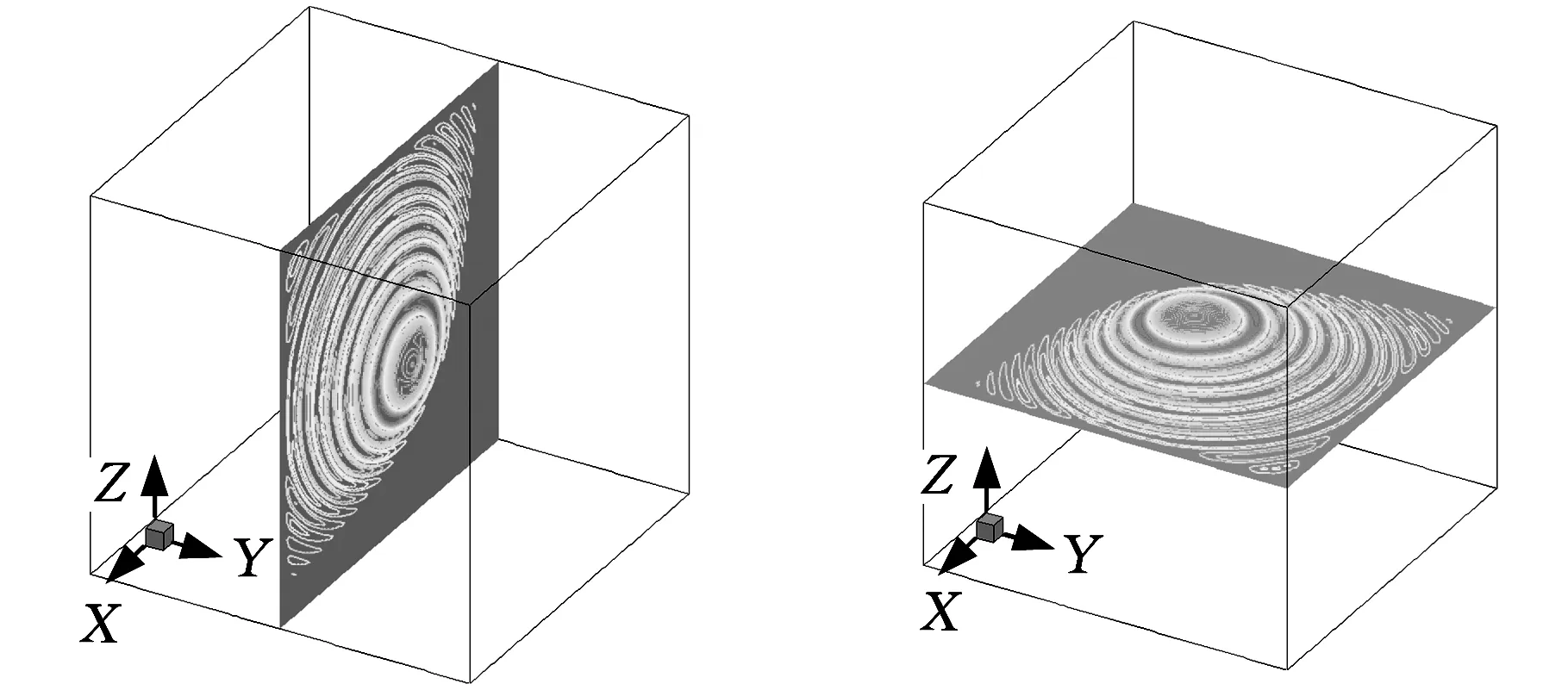
(c)平面y=0上的声压等值线图(d)平面z=0上的声压等值线图图6　t=100 s时声压等值面与等值线图

4　结论

(1)三维斜流线性欧拉方程中，涡波、熵波与声波的色散关系轨迹均存在不稳定区域。

(2)提出的坐标变换关系式能有效修正各物理波的群速度与相位速度方向，使其色散关系轨迹均稳定。

(3)提出的PML吸收边界条件能较好地吸收熵波、涡波与声波，未见明显反射。

[1]BerengerJP.APerfectlyMatchedLayerfortheAbsorptionofElectromagneticWaves[J].JournalofComputationalPhysics, 1994, 114(2): 185-200.

[2]HuFQ.OnAbsorbingBoundaryConditionsforLinearizedEulerEquationsbyaPerfectlyMatchedLayer[J].JournalofComputationalPhysics, 1996, 129(1): 201-219.

[3]HuFQ.AStablePerfectlyMatchedLayerforLinearizedEulerEquationsinUnsplitPhysicalVariables[J].JournalofComputationalPhysics, 2001, 173(2): 455-480.

[4]HuFQ.APerfectlyMatchedLayerAbsorbingBoundaryConditionforLinearizedEulerEquationswithaNon-uniformMeanFlow[J].JournalofComputationalPhysics, 2005, 208(2): 469-492.

[5]HuFQ,LiXD,LinDK.AbsorbingBoundaryConditionforNonlinearEulerandNavier-stokesEquationsBasedonthePerfectlyMatchedLayerTechnique[J].JournalofComputationalPhysics, 2008, 227(9): 4398-4424.

[6]LinDK,LiXD,HuFQ.AbsorbingBoundaryConditionforNonlinearEulerEquationsinPrimitiveVariablesBasedonthePerfectlyMatchedLayerTechnique[J].Computers&Fluids, 2011, 40(1): 333-337.

[7]ZhouY,WangZJ.AbsorbingBoundaryConditionsfortheEulerandNavier-stokesEquationswiththeSpectralDifferenceMethod[J].JournalofComputationalPhysics, 2010, 229(23): 8733-8749.

[8]柳占新, 高频, 仝志勇.全欧拉方程的理想匹配层边界条件[J].中国机械工程, 2011, 22(16): 1938-1941.

LiuZhanxin,GaoPin,TongZhiyong.PMLBoundaryConditionsforFullEulerEquations[J].ChinaMechanicalEngineering, 2011, 22(16): 1938-1941.

[9]周正干, 魏东.时域有限差分法在超声波声场特性分析中的应用[J].机械工程学报，2010, 46(2): 9-13.

ZhouZhenggan,WeiDong.AnalysisofUltrasonicSoundFieldCharacteristicwithFDTD[J].ChineseJournalofMechanicalEngineering，2010, 46(2): 9-13.

[10]ParrishSA,HuFQ.PMLAbsorbingBoundaryConditionsfortheLinearizedandNonlinearEulerEquationsintheCaseofObliqueMeanFlow[J].InternationalJournalforNumericalMethodsinFluids, 2009, 60(5): 565-589.

[11]ParrishSA.AnalysisandApplicationofPerfectlyMatchedLayerAbsorbingBoundaryConditionsforComputationalAeroacoustics[D].Norfolk:Univ.ofOldDominion, 2008.

[12]HuFQ.DevelopmentofPMLAbsorbingBoundaryConditionsforComputationalAeroacoustics:aProgressReview[J].Computers&Fluids, 2008, 37(4): 336-348.

[13]陈志夫.基于色散关系分析的高精度气动声学计算方法研究[D].长沙:湖南大学, 2013.

[14]HuFQ,HussainiMY,MantheyJL.Low-dissipationandLow-dispersionRunge-KuttaSchemesforComputationalAcoustics[J].JournalofComputationalPhysics, 1996, 124(1): 177-191.

[15]TamCKW,JayC,ZhongD.AStudyoftheShortWaveComponentsinComputationalAcoustics[J].JournalofComputationalAcoustics, 1993, 1(1): 1-30.

(编辑陈勇)

Three Dimensional Linear PML Absorbing Boundary Conditions with an Oblique Mean Flow

Wu Xin1,2Chen Zhifu3Yin Hanfeng1

1.State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body,Hunan University,Changsha,410082 2.Hunan Institute of Engineering,Xiangtan,Hunan,411104 3.Guangzhou Automobile Group Co.,Ltd. Automotive Engineering Institute,Guangzhou,511434

For three dimensional linear Euler equations in the case of oblique mean flow, the dispersion relations of acoustic, vortex and entropy wave were first analyzed by using Fourier and Laplace transform method. Then the hypothesis for changed frequency was employed, a proper space-time transformation was presented for deriving three dimensional linear Euler equations in transformed coordinates. A complex change was applied to the new equations and a damping parameter was introduced. A three linear PML absorbing boundary conditions in the case of oblique mean flow forxlayer,ylayer,zlayer and corner layer were derived. In addition, the importance of added absorption term was emphasized. Finally, the effectiveness of linear PML absorbing boundary conditions was validated by computing the computational aeroacoustics benchmark problems. The results prove that: the presented space-time transformation can solve the problem of direction inconsistence in group and phase velocity of physical wave; in the case of oblique mean flow, the proposed PML absorbing boundary conditions can absorb the physical wave with little or no reflection.Therefore,it also can be applied to aeroacoustic computation.

perfectly matched layer(PML); boundary condition; computational aeroacoustics; Euler equation; dispersion

2014-05-19

国家自然科学基金资助项目(11302075,11002052)；湖南省教育厅高等学校科学研究项目(12C0627)

V211.3DOI：10.3969/j.issn.1004-132X.2015.01.001

伍新，男，1976年生。湖南大学汽车车身先进设计制造国家重点实验室博士研究生，湖南工程学院机械工程学院讲师。主要研究方向为计算声学、振动与噪声控制。陈志夫，男，1986年生。广州汽车集团股份有限公司汽车工程研究院工程师。尹汉锋，男，1982年生。湖南大学汽车车身先进设计制造国家重点实验室讲师、博士。