关节轴承摩擦温度场计算方法

俞建卫　王礼飞　魏　巍

合肥工业大学，合肥，230009

关节轴承摩擦温度场计算方法

俞建卫王礼飞魏巍

合肥工业大学，合肥，230009

以推力型关节轴承为研究对象，分析了轴向载荷下的接触应力，并根据试验所得摩擦力矩反推出了动态摩擦因数。结合接触应力及摩擦因数求出了摩擦热流率，并将其作为第二类边界条件进行了轴承非定常温度场有限元分析，最后利用红外热像仪拍摄了摩擦过程中轴承侧表面温度分布，检验仿真结果的可靠性。仿真与试验结果表明：该计算方法解决了球面摩擦副摩擦因数的精确计算和热流率的空间分配问题，建模时忽略球面间隙会直接影响接触应力分布并造成温度场分布出现较大误差，考虑球面间隙可以更精确地计算轴承摩擦温度场。

关节轴承；球面间隙；接触应力；温度场；红外测量；有限元

0　引言

关节轴承又称球面滑动轴承，是一种摩擦副为球面的特殊滑动轴承，常在重负荷条件下做低速摆动或旋转，在军用机械、建筑及航空等众多领域均有大量应用[1-3]。润滑型关节轴承材料多数使用GCr15钢,采用淬火后低温回火处理[4],当使用温度高于回火温度时,材料硬度急剧下降,材料磨损加剧。另外,摩擦热效应还会显著降低润滑油膜的黏度,黏度的下降又会导致润滑油膜的承载能力降低,甚至导致润滑失效[5]。

研究表明：摩擦副表层或亚表层材料发生变形或撕裂时产生的能量大部分会转化为热能，引起摩擦表面温度升高并向四周传递[6]。轴承摩擦过程中摩擦面作为生热面，温度会明显高于外表面，传统的测温方法仅在轴承表面布置热电偶测量单点温度，对摩擦面及整体温度场分布缺乏研究;又由于摩擦面和轴承内部的不可见性，其温度值不宜直接获得。因此有必要对轴承展开摩擦三维非定常温度场的分析。

在平面滑动摩擦副的温度场研究中,假设接触区域压力恒定，将理论计算与实测温度对比可知,当考虑热流率随时间和旋转半径变化时，可以得到更符合实际的摩擦温度场模型[7]。但关节轴承的摩擦副为空间球面,其接触形式不同于赫兹接触，需要进行数值方法求解[8]。又由于球面间隙的存在，因此假设球面完全协调接触也会导致较大的计算误差[9]。本文先使用有限元方法分析轴承接触应力分布,结合实测摩擦力矩反求动态摩擦因数，根据摩擦生热原理计算热流率随时间和空间坐标分布,并将其作为摩擦面的第二类边界条件建立温度场模型,然后使用热像仪测试温度进行试验验证,最后基于上述方法分别研究建模时忽略球面间隙和考虑球面间隙对轴承温度场的影响。

1　试验装置与实体模型

如图1所示，以GX25S推力型油润滑关节轴承为试验试样,基于HDM-20型号端面磨损试验机设计试验夹具。试验过程中,由下平台的加载面施加向上的轴向载荷;试验机通过销槽传递扭矩,带动芯轴和内圈做顺时针单向旋转运动;轴承外圈与下平台采用过渡配合，装置在下平台的牵引螺钉连接拉力传感器，可实时测量轴承摩擦力矩；试验润滑剂为锂基润滑脂。使用Thermo VisionTMA40-M在线红外热像仪拍摄轴承表面,获得外表面实际温度分布。

图1　试验原理图

有限元建模时忽略芯轴的销槽、润滑油槽及其他细小特征的影响，则整体模型关于芯轴中心对称,为缩短计算时间将其简化为平面轴对称模型。

由于试验工况下轴承温升较小,故假设材料各项参数在温升范围内未发生变化。各材料参数如表1所示。

表1　材料属性

2　有限元模型的建立

2.1模型建立及简化

在轴承的实际结构中,为满足储存润滑油及满足转动灵活的需要,外圈的球面直径会略大于内圈的球面直径。使用ZEISS三坐标仪分别测量内外球面直径,实测值如下:外圈内径为68.1000 mm,内圈外径为67.9400 mm,两球面的曲率半径差值为0.008 mm。数据显示,内外球面在几何上存在初始的曲率半径差值(下文中将这个差值统称为球面间隙),而并非完全相同。但由于间隙值相对整体尺寸非常小,不利于有限元的建模处理，因此有研究在分析球面接触应力时忽略了球面间隙的存在,假设内外球面完全一致,但试验证明忽略间隙值会导致应力分析结果出现较大误差[9]。为研究间隙值对接触应力及温度场的影响,分别将建模时忽略间隙(内外球面直径均为68.000 mm)和考虑间隙(球面直径为实测值)作为两种不同情况进行有限元建模研究,则对球面接触可作如下假设：①忽略间隙时球面完全接触，假设内外球面接触位置的温度相同;②考虑间隙时,由于球面间隙极小并涂有大量润滑脂，内外球面存在较大的热交换，也假设内外圈球面接触位置的温度相同。

基于上述假设,在温度场计算中使用MPC算法将接触时对应球面位置的温度自由度“系”在一起。

2.2摩擦热量的计算

摩擦生热量可由下式计算[10]:

q=μp vr

(1)

式中,q为单位接触面积上产生的热量,即热流密度;μ为摩擦因数;p为接触正压力;vr为接触位置的相对线速度。

由式(1)可知,摩擦热的生成与摩擦因数、接触应力分布及相对线速度均有直接关系。

关节轴承试验机上的摩擦因数计算式为[11]

(2)

式中,M为摩擦力矩;N为载荷;dk为球面直径。

但式(1)并没有考虑加载方式和球面间隙等参数对接触应力及摩擦因数的影响,引入到热流率的计算时会导致误差较大。

采用等效离散法,在结构有限元中对模型进行网格划分,可将球面等效成一系列不同半径的圆环面接触。假设在某一载荷条件下共有n个圆环参与实际接触，忽略润滑脂的影响，则各圆环对旋转中心的摩擦力矩之和等于实测摩擦力矩。

试验过程中,设各圆环摩擦因数为μi(t),则由力矩平衡可得

(3)

为简化模型,假设各圆环摩擦因数相同,且均为μ(t),则有

(4)

式中,M(t)为实测摩擦力矩;Fi为圆环接触总反力;ri为圆环半径,且ri∈[17.25 mm,27.701 mm]。

根据式(1),摩擦生热量可表示为

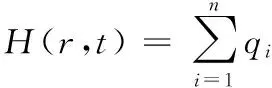
(5)

式中,H(r,t)为热流率;ω(t)为旋转角速度;Ai为圆环面积。

对任一圆环有

Fi=piAi

(6)

因此,关节轴承的球面摩擦热流率可表示为

Hi(r,t)=μ(t)Fiω(t)ri

(7)

2.3热量传导及定解条件

基于傅里叶导热定律,对各向同性的固体导热有如下方程[12]：

(8)

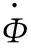
定解条件包括初始条件和边界条件。试验在室温下进行，初始温度为25 ℃。

对流换热可根据牛顿冷却公式计算：

Φ=hA(Tw-Tf)

(9)

式中,h为表面换热系数;A为表面面积;Tw和Tf分别为表面温度和环境温度。

热辐射计算为非线性,增大了收敛难度,因此将传热系数提高10%替代热辐射效果[13]。

2.4有限元计算

根据式(7)所需参数,使用APDL语言编写计算控制程序，程序流程如图2所示。

图2　APDL程序流程图

试验工况为：载荷2 kN,转速30 r/min。按照图2所示流程,程序先计算出两类模型下的接触应力分布(图3),再根据实测摩擦力矩计算出实时摩擦因数(图4),结合接触反力、摩擦因数及转速计算出热流率分布(图5),最后计算出温度场(图6)。

3　结果与分析

3.1接触应力分布

图3所示分别为两类模型的球面接触应力径向坐标的变化情况。其中无间隙模型是假设内外球面直径均为68.000 mm,轴承内外圈恰好处于完全协调接触；有间隙模型根据实测球面的曲率半径进行建模处理，轴承内外圈在初始状态下并未接触，由于载荷的施加，初始间隙被逐渐合并，并最先在球面底部产生初始接触。

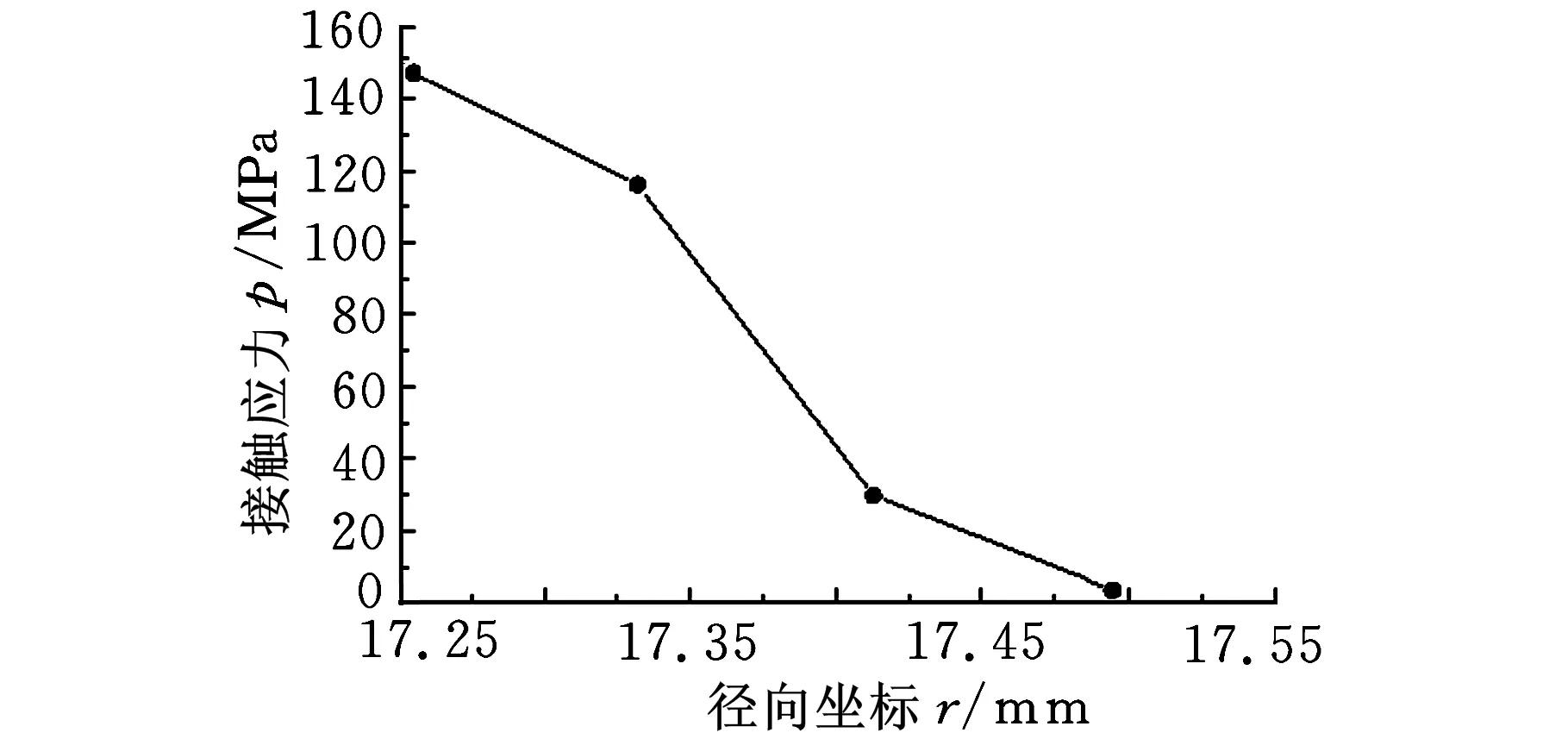
(a)轴承内外圈有间隙

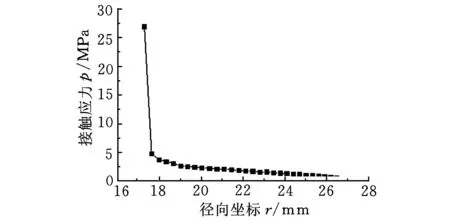
(b)忽略轴承内外圈间隙图3　接触应力

由图3可知:两类模型均在球面最底端出现最大接触应力，且均随径向坐标的增大先急剧减小，而后下降趋势趋于平缓。无间隙模型与文献[9]得到了类似的接触应力分布趋势，间隙模型接触区域的径向坐标范围远远小于无间隙情况，其最大接触应力也远远大于无间隙状态。这是因为间隙模型中球面间隙破坏了球面接触的协调性，初始接触时只有球面最底端的区域参与接触，导致其应力分布与无间隙模型出现明显差异。此外，由式(1)可知，接触应力的分布会直接影响摩擦生热量在空间上的分布;由式(4)可知,接触应力的分布也同时影响摩擦因数的反推。因此建模时考虑实际的几何间隙,可以提高热流率的计算精度。

3.2摩擦因数及热流率

图4中,在忽略间隙和计入间隙两种模型中,摩擦因数与摩擦力矩的变化趋势均保持一致,但无间隙模型反推出的摩擦因数明显小于有间隙模型反推出的摩擦因数。由于二者采用相同计算方法由相同摩擦力矩反推得到,无间隙模型中球面接触区域较大，轴承转动不灵活易造成较大摩擦力矩，因此反推出的摩擦因数较有间隙模型反推出的摩擦因数偏小。

(a)摩擦力矩

(b)摩擦因数图4　摩擦力矩及摩擦因数

图5中两类模型的热流率均随球面径向坐标和时间变化。有间隙模型中接触面上只有球面最底端附近区域有摩擦热生成，无间隙模型的热流率分布范围比有间隙模型的热流率分布范围更广,但其峰值也明显偏小。根据式(1)可知，在相同的转速下接触应力分布和摩擦因数直接决定摩擦热的分布,因此两类模型的热流率在空间上分布与接触应力分布成正比，在时间上的变化与动态摩擦因数的变化成正比。

(a)无间隙状态下热流率分布

(b)间隙状态下热流率分布图5　热流率分布

3.3温度分布及验证

图6为轴承外圈在1800 s时的温度灰度图。由图6可知:两类模型的总体温升大致相同，最高温度都出现在球面底部；但二者的温度场分布出现较大差异，无间隙模型的总体温度分布更加均匀，摩擦生热区域与轴承表面的温差较间隙模型更小。出现此类现象的原因主要为：①式(7)是将摩擦阻力做功转换成热能，因此单位时间内输入轴承的总热量相同，在相同的散热边界条件下,两类模型的总体温升也大致相同；②图6中两类模型的热流率都集中于球面底部，故大量热量输入此处形成高温区；③无间隙模型的接触区域大于间隙模型，有利于球面上生成的摩擦热向低温区扩散并形成较均匀的温度分布，而间隙模型的生热区域明显偏小，不利于温度扩散，因此摩擦面的最高温度与轴承表面出现更大的温差。

(a)无间隙模型

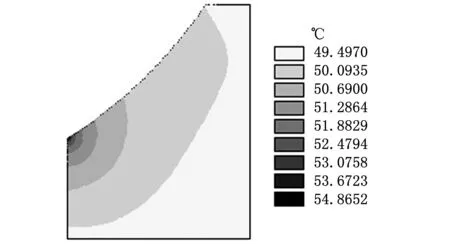
(b)有间隙模型图6　轴承外圈温度分布

取轴承外圈表面距上表面3 mm处点A(图1所示)作为温度验证点，实测温度与计算温度随时间变化曲线如图7所示。

在摩擦前期,理论计算值与测量值都以较快速度上升并基本保持一致；随着时间的延长温升速度均有所减缓，无间隙模型温度逐渐高于间隙模型温度和实测温度，实测温度低于两类模型的计算温度且差距逐渐增大。在第30 min计算值与实测值出现最大误差，实测值与无间隙模型的误差约为6.75℃,实测值与间隙模型的误差约为4.53℃。

图7　验证点温升过程对比

分析产生误差的原因为:①建模过程中将几何模型的细小特征作了简化,同时也忽略了润滑油和磨屑带走的热量，导致计算温度偏高；②有研究指出金属摩擦生热过程中摩擦力所做功约有95%转化为热量[14],而式(7)假设摩擦力做功全部转化为热能也会造成理论计算温度高于实测温度;③无间隙模型的热量流入范围较大，热源距离测温点的距离也较间隙模型更近,导致A点温升高于间隙模型的温升，同时误差也大于间隙模型的误差。另外，由于球面间隙较小，高温导致的热变形会改变球面的接触面积，进而影响热流率在空间上的分配，当使用温度较高时需要进一步考虑热力耦合的影响。

4　结论

(1)球面间隙的存在对球面接触应力分布、摩擦因数及摩擦热的生成均有重要影响，建模时忽略间隙值会产生较大误差。

(2)摩擦产生的热流率随时间和空间坐标动态变化,其中动态的摩擦因数决定热流率在时间上的变化规律，接触应力分布决定热流率在空间上的能量分配。

(3)根据间隙模型的分析结果，当轴承使用温度在50 ℃左右时，内部高温区比轴承表面温度高出约5℃，因此，在试验中通过测量表面温度判断轴承实际温升的方法存在较大误差。

(4)依据本文建立的间隙模型,在已知轴承尺寸、材料参数及换热条件的情况下，结合试验所得摩擦力矩可以反推实时摩擦因数和热流率分布。

[1]Kim B C,Park D C,Kim H S,et al.Development of Composite Spherical Bearing[J].Composite Structures,2006,75(1):231-240.

[2]潘汉明,陈以一,赵宪忠,等.广州新电视塔双向铰节点试验研究[J].工业建筑,2009(1):117-121.

Pan Hanming,Chen Yiyi,Zhao Xianzhong,et al.Experimental Study on Bidirectional Pin-hinged Joints of Guangzhou New TV Tower[J].Industrial Construction,2009(1):117-121.

[3]Germaneau A,Peyruseigt F,Mistou S,et al.3D Mechanical Analysis of Aeronautical Plain Bearings:Validation of a Finite Element Model from Measurement of Displacement Fields by Digital Volume Correlation and Optical Scanning Tomography[J].Optics and Lasers in Engineering，2010,48(6):676-683.

[4]《机械工程材料性能数据手册》编委会.机械工程材料性能数据手册[M].北京:机械工业出版社,1995．

[5]温诗铸, 黄平. 摩擦学原理[M].北京：清华大学出版社有限公司, 2002.

[6]Yang Jianheng.Analysis to the Thermal Mechanism of Wear in Dry Friction Condition[J].Lubrication Engineering,2005,171(5):173-176.

[7]魏巍,俞建卫,沈持正,等.基于试验数据的滑动摩擦温度场仿真方法研究[J].中国机械工程,2013,24(18):2426-2430.

Wei Wei,Yu Jianwei,Shen Chizheng,et al.Research on Sliding Friction Temperature Field Simulation Method Based on Experimental Data[J].China Mechanical Engineering,2013,24(18):2426-2430.

[8]Germaneau A,Peyruseigt F,Mistou S,et al.Verification of a Spherical Plain Bearing Finite-element Model Using Scattered Light Photoelasticity Tests[J].Proceedings of the Institution of Mechanical Engineers,Part J:Journal of Engineering Tribology,2008,222(5):647-656.

[9]刘六井,高伟.大型推力关节轴承结构有限元分析[J].船海工程,2004(2):25-27.

Liu Liujing,Gao Wei.The Structure Finite Element Analysis of Large-scale Thrust Jiont Bearing[J].Ship and Ocean Engineering,2004(2):25-27.

[10]Yang Y C,Chen W L.A Nonlinear Inverse Problem in Estimating the Heat Flux of the Disc in a Disc Brake System[J].Applied Thermal Engineering,2011,31(14):2439-2448.

[11]王国锋. 复合摆动式关节轴承性能试验机的研制及试验研究[D].洛阳:河南科技大学, 2011.

[12]杨世铭,陶文铨.传热学[M].3版.北京:高等教育出版社, 1998.

[13]李奇亮. 基于界面测温的面接触摩擦温度场研究[D].合肥:合肥工业大学,2009.

[14]Majcherczak D,Dufrenoy P,Berthier Y.Tribological Thermal and Mechanical Coupling Aspects of the Dry Sliding Contact[J].Tribology International,2007,40:834-843.

(编辑王艳丽)

Calculation Method of Spherical Plain Bearing Friction Temperature Field

Yu JianweiWang LifeiWei Wei

Hefei University of Technology,Hefei,230009

Taking thrust spherical plain bearing as the research object,the contact stress under axial load was analyzed and based on the experimental friction torque the dynamic friction coefficient was solved.Then combined with contact stress and friction coefficient,heat flow rate was calculated and served as the second boundary condition for the unsteady temperature field finite element analysis of the bearing.Finally,using infrared camera to shoot the outer surface of two-dimensional temperature distribution of the bearing friction process,then reliability of simulation results was tested.Simulation and experimental results show that: the calculation method has solved the problems of accurate calculation of spherical friction coefficient and spatial distribution of the heat flow rate.Ignoring the spherical gap when modeling will affect the contact stress distribution directly and cause a larger error in temperature distribution.Considering a spherical gap a more accurate bearing friction temperature field can be obtained.

spherical plain bearing;spherical gap;contact stress;temperature field;infrared measurement;finite element

2014-06-13

国家自然科学基金资助项目(51075114)

TH117.1DOI：10.3969/j.issn.1004-132X.2015.10.002

俞建卫,男,1956年生。合肥工业大学摩擦学研究所及安徽省粉末冶金工程技术研究中心研究员。主要研究方向为摩擦学测试技术。王礼飞,男,1991年生。合肥工业大学机械与汽车工程学院硕士研究生。魏巍，男，1986年生。合肥工业大学仪器科学与光电工程学院博士研究生。