基于白光扫描干涉的振动补偿方法

茅　健　徐　朋　杨将新　曹衍龙

1.上海工程技术大学,上海,201620　　2.浙江大学,杭州,310027

基于白光扫描干涉的振动补偿方法

茅健1徐朋2杨将新2曹衍龙2

1.上海工程技术大学,上海,2016202.浙江大学,杭州,310027

研制了一种基于白光波长扫描干涉法的表面形貌抗振反馈测量系统,介绍了白光扫描干涉法的相位提取算法和相位去包裹算法，对声光可调滤光器低速率扫频时产生的非线性误差进行了算法修正，设计了用于振动补偿的DSP硬件控制模块，并搭建了抗振反馈测量系统。在不同振动环境下，对研磨12级的标准样块进行了三维表面形貌测量以及粗糙度参数评定。结果表明,施加低频振源后的粗糙度评定参数大小为未施加任何振源的粗糙度评定参数大小的2倍左右,开启系统振动反馈后，粗糙度评定参数接近最大允许值，说明本测量方法能在一定程度上消除振动噪声的影响，保证测量的顺利进行。二维、三维表面评定结果对比表明，三维表面评定能更全面地表现被测表面的形貌特征。

白光扫描干涉;相位计算;振动补偿;表面评定

0　引言

白光干涉测量是指从干涉光强信息中提取每一点相位值的测量技术,在实际测量环境中，扰动和误差不可避免，因此较难得到真实的相位值[1]。在有干扰的情况下，应先获得干涉信号的相位值，通过一定的反馈补偿算法获取振动量的大小，以消除振动带来的影响[2]。

相移干涉(phase shifting interferometry)是将数字相移技术引入到干涉测量技术中而发展起来的一项光学干涉测量技术，在高精度测量领域有着非常重要的地位[3]。传统的相移干涉技术通常采用激光或单波长的光源作为系统测量光源，由于干涉光波振动具有周期性，使用激光作为光源有可能产生相位不确定性问题[4],因此,它不适用于非连续表面和有台阶突变的表面测量。为了解决这一问题，出现了许多新的测量方法[5-8]。然而光学干涉测量技术对环境噪声非常敏感，振动环境下的干涉测量技术主要有主动式抗振和被动式抗振两种。Han等[9]提出的最小二乘拟合法可修正测量过程中的随机误差和非线性误差。Phillion[10]提出的算法可以补偿特定频率的小幅度振动。吴栋等[11]设计了一种机电反馈式干涉仪,当存在振动时,被测相位发生变化，压电陶瓷(PZT)控制器输出反馈信号驱动PZT移动，改变两相干光束的光程差，实现振动补偿。赵智亮等[12]研究了基于迭代最小二乘算法的相移误差修正算法，实现了任意两幅干涉图间相对移相量的计算。

虽然光学测量有了长足的发展，但目前尚无法大规模地应用于工业现场。本文基于白光波长扫描干涉原理，结合主动抗振技术，提出了一种抗振反馈补偿方法，研制了基于白光波长扫描干涉法的表面形貌抗振反馈测量系统，对标准样块进行了三维表面形貌的测量及评定。

1　测量系统

白光波长扫描干涉法使用白光作为测量光源，通过波长扫描装置——声光可调滤光器(acousto-optic tunable filter,AOTF)实现对白光波长的线性扫描。当控制波长连续变化时,干涉相位发生变化,从而干涉条纹的光强也产生相应的变化。通过CCD相机采集干涉图像，经过处理即可得出被测工件的表面形貌。

为了对测量环境振动干扰作出有效抑制，有必要增加一个抗振反馈模块，通常补偿方式是附加一个激光光源或单波长光源作为参考干涉仪的光源[13]。本文提出一种新的振动补偿方法:测量系统增加一个分光镜，它将干涉信号分成两路光，一路光经过透镜，所形成的干涉图像由主干涉仪中的面型探测器CCD采集，并进入计算机处理，以此获取工件表面的三维形貌；另一路光经过透镜，干涉信号由参考干涉仪中的点型光电探测器采集，并进入数字信号处理器(digital signal processor,DSP)模块进行处理，以此补偿环境噪声的影响。

本文方法使测量系统中不需添加额外的单波长光源，简化了布局结构,提高了系统的稳定性和经济性。同时为了更精确地获得环境噪声的振动补偿值，提出了AOTF的双模态工作方式。

(1)测量工作模式。通过计算机控制单片机电路输出低频率方波信号，使AOTF工作在低速率扫频模式，用以配合帧采集速率较低的CCD获取干涉图像。

(2)补偿工作模式。在CCD的帧图像曝光间隙之间，AOTF切换到高速率扫频模式，光电探测器采集快速变化的光强信号，用以快速计算并补偿由振动引起的光程差的变化。

系统中反馈控制信号由DSP控制模块计算产生,借助DSP处理速度快的特点，将补偿值快速反馈给附加在参考反射镜上的PZT实现补偿。测量系统包括主测量模块和抗振反馈模块两部分，主测量模块负责工件表面形貌的提取，包括干涉仪、声光滤光器模块、CCD图像采集模块等几部分；抗振反馈模块负责振动干扰的消除，包括干涉仪、光电探测器、DSP反馈控制器和PZT等几部分。系统软硬件总体结构如图1所示。

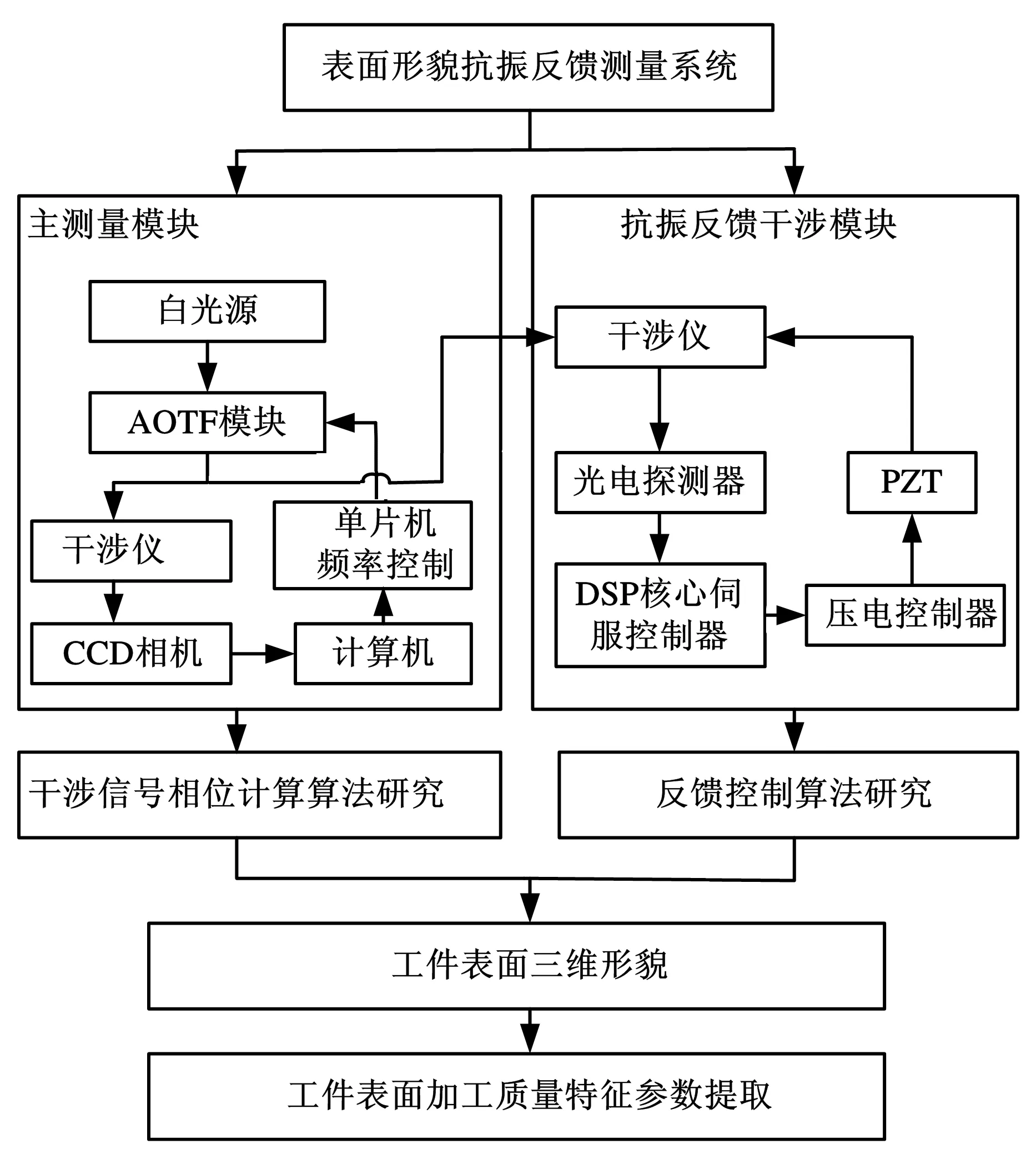
图1　抗振反馈测量系统总体结构

2　测量方法

在白光波长扫描干涉测量中，不同波长下的干涉光强信号会受到原始白光信号的影响，因此在相位提取之前，需要对原始干涉信号进行以下预处理：将干涉信号除以白光背景信号，以补偿光源谱强度和探测器响应的不一致性并使信号幅值平均化，然后对光谱信号进行平滑滤波处理，以去除干涉信号上掺杂的电噪声，从而增加相位测量的精度。本文利用傅里叶变换法进行相位提取。

2.1傅里叶变换法

傅里叶变换法由Kinoshita等[14]提出,具有较快的运算速度[15],在信噪比较低的情况下，测量误差也较小。它是通过对干涉光强信号进行傅里叶变换，并进行频域滤波来分离出相位的。干涉光强信号是与波数相关的函数,故光探测器所获取的干涉光强信号可表示为

I(k)=I1(k)+I2(k)+

(1)

式中,k为波数;I1(k)、I2(k)分别为从参考反射镜和被测物反射回的光强信号;hOPD为绝对光程差。

为了方便对式(1)进行频域变换,根据欧拉公式可得

I(f)=I0(f)+J(f-hOPD)+J(f+hOPD)

(2)

式(2)中的三项频谱可以相互分离，对J(f-hOPD)项进行反傅里叶变换，有

(3)

其中,等式右边的分子和分母分别表示对J(f-hOPD)项进行反傅里叶变换后的虚部和实部。由式(3)所求得的相位可采用相位去包裹算法展开，并重写式(3)，可得相位值：

φ(k)=2πkhOPD

(4)

2.2算法修正

在AOTF低速率扫频模式下,波数随时间以较低的速率线性变化,但在实际测量实验中,并不能保证波数绝对线性变化。为了补偿AOTF扫频的非线性误差,在计算绝对光程差时，需要对其进行修正。

测量中使用一已知高度的标准块作为参考进行高度校正,将高度为hS的标准块置于参考反射镜上,使光分别在参考反射镜和标准块表面反射并形成干涉条纹。由式(4)可知,对任意测量点(x,y)有

φ(x,y;t)=2πk(t)h(x,y)

(5)

这样可得任意待测点的高度值:

(6)

式中,(xR,yR)为参考反射镜的入射点；(xS,yS)为标准块的入射点。

通过对时间求导，可消除或减小波数k(t)随时间变化的非线性误差的影响。从式(6)可以看出,相当于在扫频期间对时间做了平均化处理，从而提高了工件表面形貌的测量精度。

通常相移算法、傅里叶变换法等利用反三角函数来获取相位，其分布区间为[-π,π],此时获得的相位是有阶跃突变的,为了得到连续变化的相位，需对相位进行去包裹处理[16]。由于三角函数以2π为分布周期,故可通过加减2kπ(k=0,1,…,n)来进行修正。此方法也被称作相位追踪法,其主要原理是将反三角函数获得的相位值看作实际相位值的包裹运算。引入两个数学算子：包裹算子W和求差算子Δ,可得

(7)

式中，φ(n)为实际相位值,即去包裹后的相位值;W1(φ(n))为利用反三角函数获得的相位值，即包裹相位值。

对傅里叶变换法得到的包裹相位,采用去包裹算法，可将包裹相位展开成连续线性变化的相位。

2.3振动补偿算法

进行反馈补偿时,AOTF工作在高速率扫频模式下,光电探测器采集干涉信号,DSP处理器进行快速处理,补偿振动引起的光程差变化。当AOTF进行高速率波长扫描时,波数随时间线性变化,导致相位发生周期性变化,同时环境噪声对干涉仪的干扰使得相位产生随机性的变化。

因此,在时刻t所获得的相位可表示为

φ(t)=4πk(t)h(t)

(8)

其中,φ(t)可通过前述相位计算算法获得;k(t)为随时间快速变化的波数,与AOTF的控制相关;h(t)为由振动引起的单臂光程差的改变量。

在t+Δt时刻，需要补偿的由振动引起的距离为

Δh=h(t+Δt)-h(t)=

(9)

式中,t、t+Δt分别为CCD采集的帧图像曝光的起始和结束时刻。

3　实验

为验证本文所提出测量方法的可行性，搭建了表面形貌测量系统。在没有振动和施加低频振源的情况下，分别对被测工件进行测试，得出被测工件的表面形貌，提取出关键粗糙度评定参数，进行对比验证。

采用的测试工件为潍坊量具厂生产的标准样块，为研磨12级,表面算术平均偏差、表面最大高度、表面十点高度、表面均方根偏差为评定参数。在隔振台上,不施加任何振源，测得的样块表面形貌如图2a所示。当在隔振台旁,用气泵施加小幅振动后,所测的表面形貌如图2b所示。系统开启抗振补偿后,所得的表面形貌如图2c所示。使用加速度传感器采集振动信号，对其进行傅里叶变换，以检测所施加的振动信号的频率。

(a)不施加任何振源表面形貌

(b)施加小幅振动后表面形貌

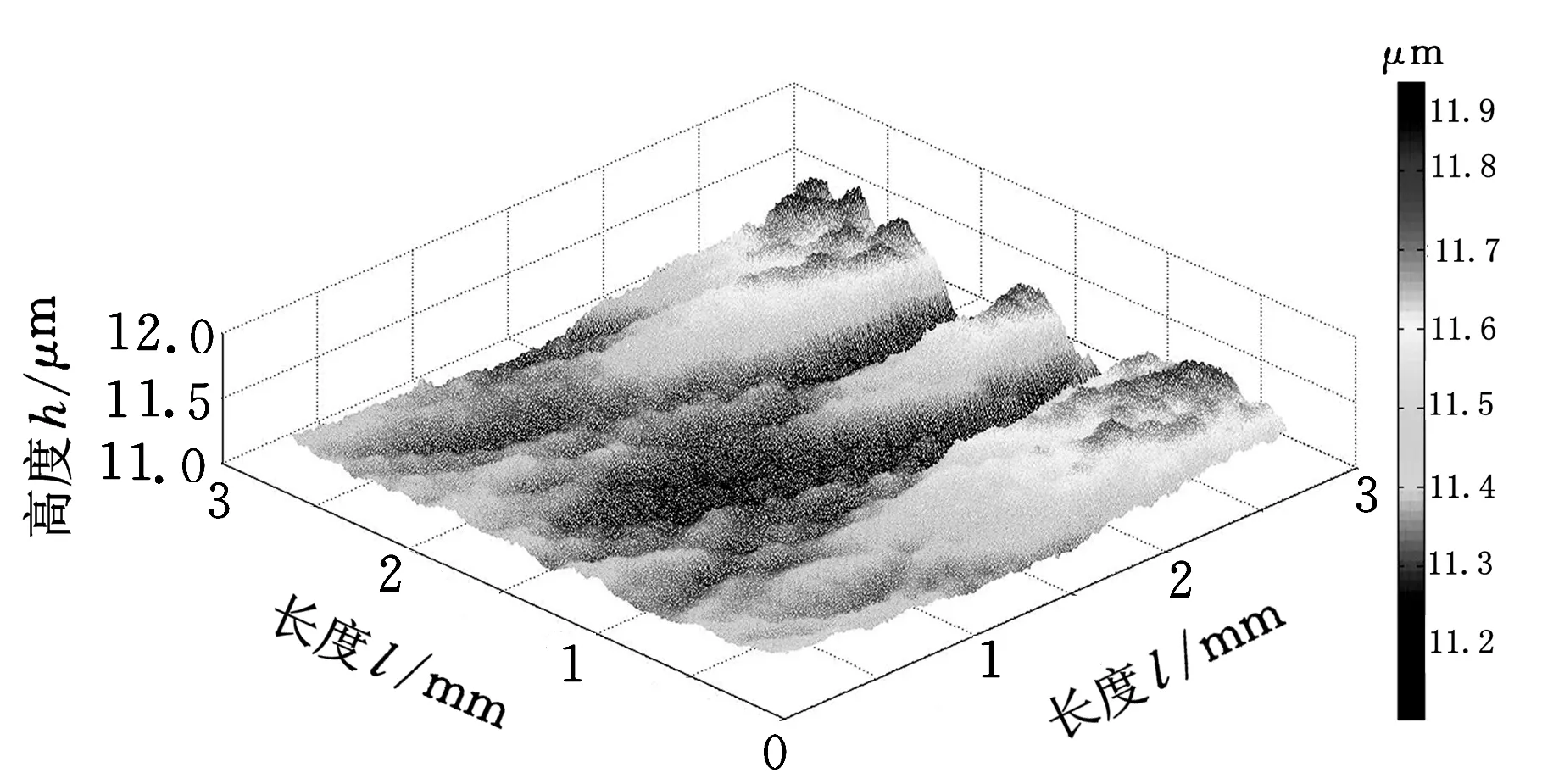
(c)振动补偿后表面形貌图2　三种情况下的表面三维形貌

获得被测样块表面形貌后,使用二维高斯滤波法对其进行滤波,建立高斯滤波基准面，综合表面三维形貌与高斯滤波基准面，得到表面粗糙度特征的三维表面评定参数如表1所示。限于篇幅，本文只列出了不施加振源的高斯滤波基准面及表面粗糙度特征，如图3和图4所示。高斯回归滤波处理后得到高斯滤波基准面，表面形貌值与高斯滤波基准面相减即可得到表面粗糙度特征，从而可以提取出所需的粗糙度评定参数。

表1　三种情况下的三维表面评定参数　μm

图3　不施加振源的高斯滤波基准面

图4　不施加振源的表面粗糙度特征

从表1可以看出,在未施加任何振源的情况下,表面算术平均偏差小于轮廓算术平均偏差Ra的最大允许值0.05μm;当人为施加低频振源后,测量出现较大偏差,测得的表面算术平均偏差大于最大允许值;当开启系统振动反馈后,测得的表面算术平均偏差小于最大允许值,说明本测量方法能在一定程度上消除振动噪声的影响，保证测量的顺利进行。

为了与二维表面评定参数进行对比，分别取不同振动等级下的三组数据进行比较，结果如表2所示。

表2　不同振动等级下的二维、三维表面评定参数对比　μm

表2显示了不同振动等级下的二维、三维表面评定参数。通过对比发现，表面算术平均偏差、表面最大高度、表面十点高度均大于对应的二维评定最大允许值，这是由于被测面进行二维粗糙度评定只能反映表面的局部信息，诸如沟槽、尖刺等表面畸变信息都有可能丢失。而三维表面评定则更具整体性，更能全面地表现被测表面的形貌特征。

4　结语

本文提出了一种白光波长扫描干涉振动补偿测量方法，利用白光波长扫描干涉法的相位提取算法和相位去包裹算法对AOTF低速率扫频时产生的非线性误差进行了算法修正，从而提高了表面形貌的测量精度。搭建了表面形貌测量系统，在无振源和施加一定振源的情况下，分别对标准样块进行了三维表面形貌的测量与参数评定，并对比了二维、三维的表面评定，实验结果表明三维表面评定更能全面地表现被测表面的形貌特征，验证了本系统的有效性。

[1]常素萍,谢铁邦.基于白光干涉的MEMS三维表面形貌测量[J].华中科技大学学报(自然科学版)，2007,35(9):8-11.

Chang Suping,Xie Tiebang.The Three-dimensional Surface Topography Measurement Based on the MEMS of White Light Interference[J].Journal of Huazhong University of Science and Technology(Natural Science Edition),2007,35(9):8-11.

[2]Sandoz P,Tribillon G,Perrin H.High-resolution Profilometry by Using Phase Calculation Algorithms for Spectroscopic Analysis of White-light Interferograms[J].Journal of Modern Optics,1996,43(4):701-708.

[3]曲芳,钟金钢.数字相移技术用于不连续复杂物体的三维面形测量[J].光学技术,2004(4):478-483.

Qu Fang,Zhong Jingang.The Digital Phase Shifting Technique Used for Three-dimensional Discrete Complex Objects Shape Measurement[J].Optical Technology,2004(4):478-483.

[4]Dresel T,Häusler G,Venzke H.Three-dimensional Sensing of Rough Surfaces by Coherence Radar[J].Applied Optics,1992,31(7):919-925.

[5]Balasubramanian N,Calif L S.Optical System for Surface Topography Measurement:US,4340306[P].1982-02-04.

[6]李朝辉,井文才,周革,等.相移干涉三维形貌纳米检测及算法研究[J].纳米技术与精密工程,2004(3):27-31．

Li Chaohui,Jin Wencai,Zhou Ge,et al.Phase-shifting Interferometry and Three-dimensional Morphology of Nano-detection Algorithm[J].Nanotechnology and Precision Engineering,2004(3):27-31.

[7]戴蓉.基于垂直扫描工作台的白光干涉表面形貌测量系统研究[D].武汉:华中科技大学,2007.

[8]王淑珍,谢铁邦,常素萍.复合型超精密表面形貌测量仪[J].光学精密工程,2011,19(4):828-835.

Wang Shuzhen,Xie Tiebang,Chang Suping.Ultra-precision Complex Surface Topography Measuring Instrument[J].Optics and Precision Engineering[J].2011,19(4):828-835.

[9]Han G,Kim S.Numerical Correction of Reference Phases in Phase-shifting Interferometry by Iterative Least-squares Fitting[J].Applied Optics,1994,33(31):7321-7325.

[10]Phillion D.General Methods for Generating Phase-shifting Interferometry Algorithms[J].Applied Optics,1997,36(31):8098-8115.

[11]吴栋,朱日宏,陈磊.移相式激光干涉仪抗振技术的研究进展[J].激光与光电子学进展,2004,41(6):25-29．

Wu Dong,Zhu Rihong,Chen Lei.Phase-shift Laser Interferometer Vibration Research Progress[J].Laser & Optoelectronics Progress,2004,41(6):25-29.

[12]赵智亮,夏伯才,陈立华.相移干涉测量中相移误差的自修正[J].光学精密工程,2013,21(5)：1116-2212．

Zhao Zhiling,Xia Bocai,Chen Lihua.Phase Shifting Interferometry Self-correction Phase Shift Error[J].Optics and Precision Engineering,2013,21(5):1116-2212.

[13]Martin H,Wang K,Jiang X.Vibration Compensating Beam Scanning Interferometer for Surface Measurement.Applied Optics,2008,47(7):888-893.

[14]Kinoshita M,Takeda M,Yago H.Optical Frequency-domain Imaging Microprofilometry with a Frequency- tunable Liquid-crystal Fabry-perot Etalon Device[J]. Applied Optics,1999,38(34):7063-7068.

[15]Wang K,Cao Y.Performance Comparison of Optical Path Difference Calculation Algorithms for Wavelength Scanning Interferometry[J].Proc. of SPIE,2010,7656:76560V-1-76560V-8.

[16]何向同.基于相移干涉的MEMS变形镜平面度测试系统误差分析与校正[D].合肥:中国科学技术大学,2009.

(编辑王艳丽)

A Vibration Compensation Method Based on White-light Wavelength Scanning Interferometry

Mao Jian1Xu Peng2Yang Jiangxin2Cao Yanlong2

1.Shanghai University of Engineering Science,Shanghai,201620 2.Zhejiang University,Hangzhou,310027

A surface topography measurement system with vibration compensation was developed herein based on the white-light wavelength scanning interferometry.Both of phase extraction algorithm and phase unwrapping algorithm was analyzed for the white-light wavelength scanning interferometry.They could be used to modify the nonlinear errors during the acousto-optic tunable filter(AOTF) swept at low rate.The hardware control module was designed for the vibration compensation.In order to verify the designed system,both of 3-dimensional(3D) surface topography and the roughness parameter of the standard sample grinding at level 12 were evaluated under different vibration environments.The results demonstrate that the measurement results with low frequency vibration are about two times than those of without vibration.After opening the system vibration feedback,the results approache to the maximum allowed value.It shows that the proposed method can eliminate the vibration effect in a certain extent.Compared with two dimensional(2D) surface evaluation results,3D surface evaluation can express the measured topography surface comprehensively.

white-light wavelength scanning interferometry;phase calculation;vibration compensation;surface evaluation

2014-05-20

国家重点基础研究发展计划(973计划)资助项目(2011CB706505);国家自然科学基金资助项目(51175322)

TH744DOI：10.3969/j.issn.1004-132X.2015.10.005

茅健，男，1972年生。上海工程技术大学机械工程学院副教授。主要研究方向为精密检测与控制、计算机辅助精度设计。徐朋,男,1988年生。浙江大学机械工程学院硕士研究生。杨将新,男,1965年生。浙江大学机械工程学院教授、博士研究生导师。曹衍龙(通信作者),男,1975年生。浙江大学机械工程学院教授、博士研究生导师。