套齿联轴器对航空发动机振动特性的影响

廖仲坤　陈　果　王海飞

1.中国航天飞航技术研究院北京动力机械研究所,北京,1000742.南京航空航天大学,南京,211106

套齿联轴器对航空发动机振动特性的影响

廖仲坤1陈果2王海飞2

1.中国航天飞航技术研究院北京动力机械研究所,北京,1000742.南京航空航天大学,南京,211106

研究了航空发动机套齿联轴器的连接刚度，推导了套齿动态啮合力计算模型，分析了随扭矩、套齿不对中和动态相对位移变化的套齿啮合力和啮合刚度。依据航空发动机套齿连接结构，建立了含套齿联轴器的三支点转子动力学模型，分析了套齿连接刚度对系统频率响应特性的影响，在考虑转轴间角度不对中的情况下，分析了套齿连接刚度对系统不对中响应的影响规律。结果发现，动态啮合力模型能够更加真实地模拟套齿连接刚度的变化，但是，当其径向啮合刚度变化不大时，其计算结果与等效刚度模型的计算结果相同，套齿角向刚度对系统动力性能影响很大，在套齿设计、装配和使用中需要重视。

航空发动机；套齿联轴器；啮合刚度；不对中；振动特性

0　引言

套齿联轴器在航空发动机中被广泛采用[1]。套齿联轴器振动过程中,内外套齿的相对位移、装配和使用所导致的内外套齿不对中，以及传递扭矩的耦合作用会在很大程度上影响套齿的啮合情况，进而改变其连接刚度,并由此对航空发动机整机振动造成很大影响。

目前，国内外对联轴器不对中的建模方法基本上有3种[2]： ①基于联轴器的变形几何关系和受力分析推导出不对中联轴器激振力模型[3-6]；②基于等效轴段法，将联轴器连接的整体系统看成是一个多跨轴盘系统，其中的联轴器用等效的轴段来模拟[7];③基于系统整体的拉格朗日能量方程，获得系统运动微分方程[8-11]。其中，等效轴段法相当于给系统增加了一个约束，而对联轴器在整体系统中的耦合作用没有充分体现；拉格朗日能量法不适合研究复杂的自由度数目较多的多跨转子系统。而直接从分析套齿啮合力出发，研究套齿啮合刚度的变化规律及其对系统整体动力响应的影响，是最为适合的方法。

有鉴于此，本文在现有研究基础上，充分考虑内外齿套间的不对中、动态相对位移以及传递的扭矩的耦合作用,动态计算出其瞬间啮合力，以充分考虑套齿联轴器在运动过程中的变刚度特征。同时，依据实际航空发动机的套齿联轴器模型，建立了含套齿联轴器的三支点转子动力学模型，研究了套齿连接刚度对系统频率响应和不对中故障振动响应的影响。

1　单齿啮合刚度计算

1.1单齿啮合刚度

假定润滑情况良好,忽略齿面接触之间的摩擦，齿轮的综合啮合刚度是指在整个啮合区中参与啮合的各对齿轮的啮合刚度的总和,单齿的弹性变形是单个轮齿的啮合齿面在载荷作用下的弹性变形。直齿轮轮齿一般处理成二维平面问题，相应的受载弹性变形计算方法有材料力学方法、弹性力学方法及有限元方法等，其中材料力学法是最早使用、应用最广的方法。单个轮齿模型如图1所示。

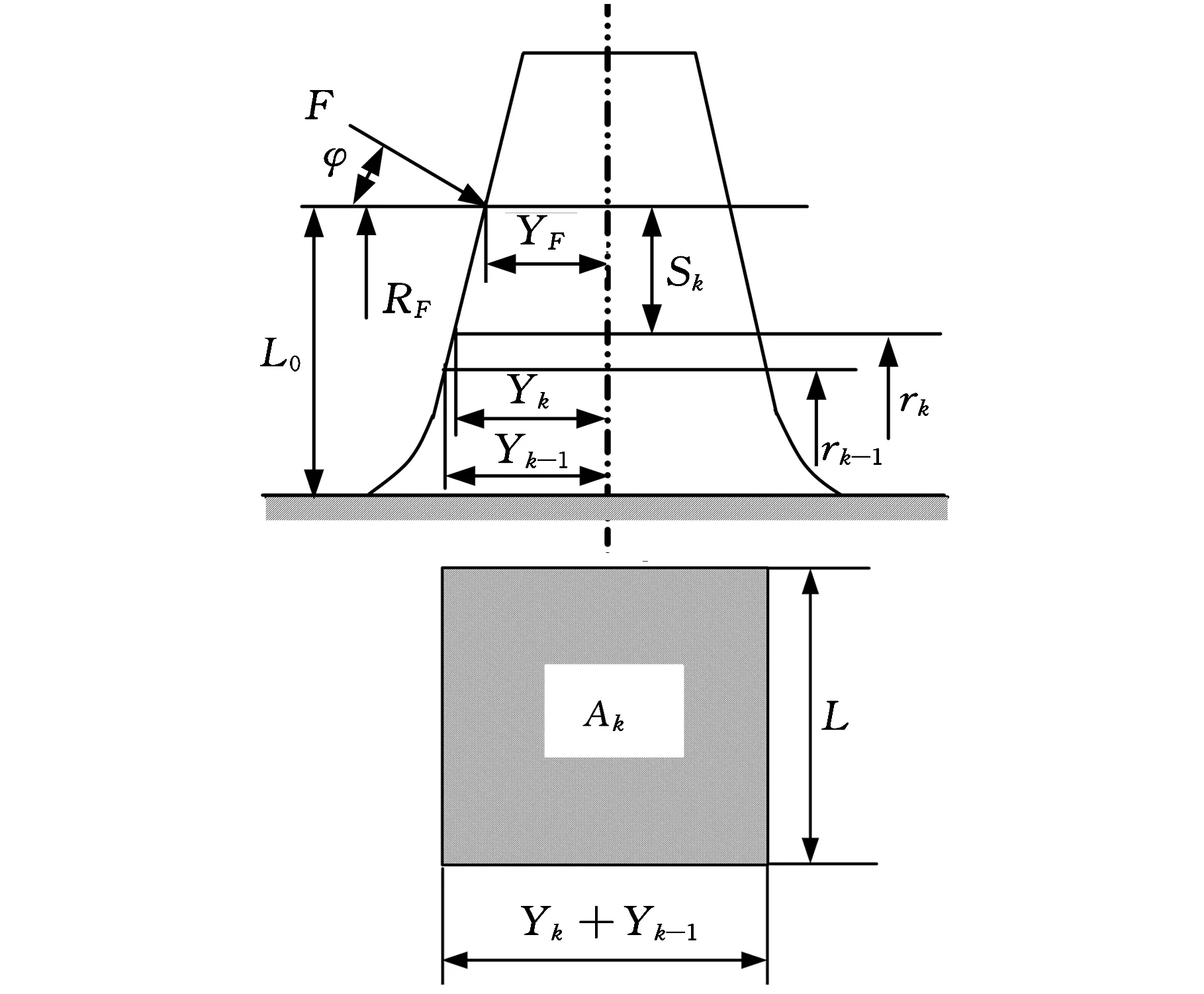
图1　单个轮齿模型

单个齿可视为具有均匀横截面的q个受载微齿段组成，图1中，φ为节圆压力角,F为齿之间相互的作用力。对于侧面啮合情况，假设作用力F以集中力形式沿法向作用于节圆上。设L为齿长度,Yk及Yk-1为第k微齿段上下表面半齿宽，rk及rk-1为第k微齿段上下表面半径,RF为力F的作用点的半径。齿段面积、惯性矩等参数分别由以下计算式求出：

(1)第k微齿段上下表面平均面积Ak=L(Yk+Yk-1)。

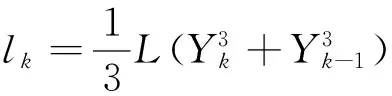
(3)第k微齿段高度hk=Yk-Yk-1。

(4)第k微齿段上表面到节圆距离Sk=RF-rk。

(5)载荷等效啮合距离为L0,在内外套齿对中的情况下，对于外齿，L0为节圆半径与外齿小圆半径之差，即L0=R-R1，其中,R为节圆半径,R1为外齿小圆半径；对于内齿,L0为内齿大圆半径与节圆半径之差，即L0=R2-R,其中，R2为内齿大圆半径。

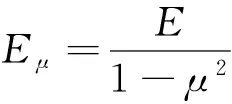
上述各式均可用于齿的渐开线部位及齿根部位的各个齿段。需要注意的是，在计算过程中，需要计算任意圆周上的齿厚，对于外齿套，其计算公式为

对于内齿套，其计算公式为

φk=arccos(rk/R)invφk=tanφk-φk

式中,m为齿轮模数,πm为齿距,即外齿套与内齿套的齿厚之和;S为节圆处齿厚,S=m/2;节圆半径R=Zm/2;Z为齿数；对于外齿套,rk=R1+khk,对于内齿套，rk=R+khk。

先求出该模型由单位载荷引起的位移(即柔度)，再求其倒数(即刚度)。其位移分别由弯曲、剪切、支座弹性、齿面挤压四种机械变形引起。一般情况下，由于轴的弹性引起的变形较小，不需修正,且不考虑材料屈服挤压情况，因此可仅考虑弯曲变形及剪切变形。

(1)弯曲变形。单齿的弯曲柔度Δb为

(1)

(2)剪切变形。设Ak为横截面面积，B为截面形状系数，对于矩形截面,B=1.2，则单齿的剪切柔度Δs为

(2)

式中，G为套齿材料剪切模量。

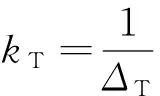
1.2套齿动态啮合力

在内外套齿完全对中时，内外联轴器圆心重合，此时各齿啮合距离均为齿根高，当系统存在不对中时，设x向、y向不对中量分别为x0、y0，则径向不对中量e为

(3)

设径向不对中量e与x向夹角为θ,则有

cosθ=x0/esinθ=y0/e

由于套齿不对中情况的出现，此时内外套齿的啮合是不均匀的，有的齿对啮合紧密，有的齿对啮合疏松，两个圆心不重合，内套齿各个齿的啮合距离不相等，沿不对中方向θ,齿对啮合最紧密，如图2b所示。在坐标系oxy下，x轴正上方的齿的编号为1，逆时针依次为2, 3, 4,，各齿与x轴正向的夹角为αj=2π(j-1)/Z(j为齿的编号),各齿的等效啮合距离为Lj=L0-ecos(αj-θ),因此,不对中套齿联轴器各齿对的啮合刚度为

kj=f(Lj)

(4)

(a)完全对中(b)不对中

(c)齿的受力图2　不对中对套齿的啮合力影响

套齿联轴器的内齿和外齿啮合时，在节圆上，单个齿的法向力Fnj可分解为两个相互垂直的分力，即圆周力Ftj和径向力Frj，如图2c所示。它们之间的关系为

(5)

式中,Tj为第j个单齿传递的扭矩。

联轴器传递的扭矩为

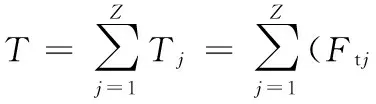
(6)

单个齿的法向力Fnj为

(7)

式中,L1j为外齿套上的啮合距离;λj为各齿沿法向力Fnj方向的变形;β为各齿变形产生的扭转角位移。

设扭矩引起的各个齿的扭转角位移相同，则有

(8)

因此

(9)

所以，由于扭矩产生的轮齿法向的变形为

(10)

设内外齿套在坐标系oxy中的相对位移为Δx和Δy，由齿轮的啮合关系，通过坐标旋转，可以得到在坐标系o1tn中的位移Δt和Δn，如图3所示，即

(11)

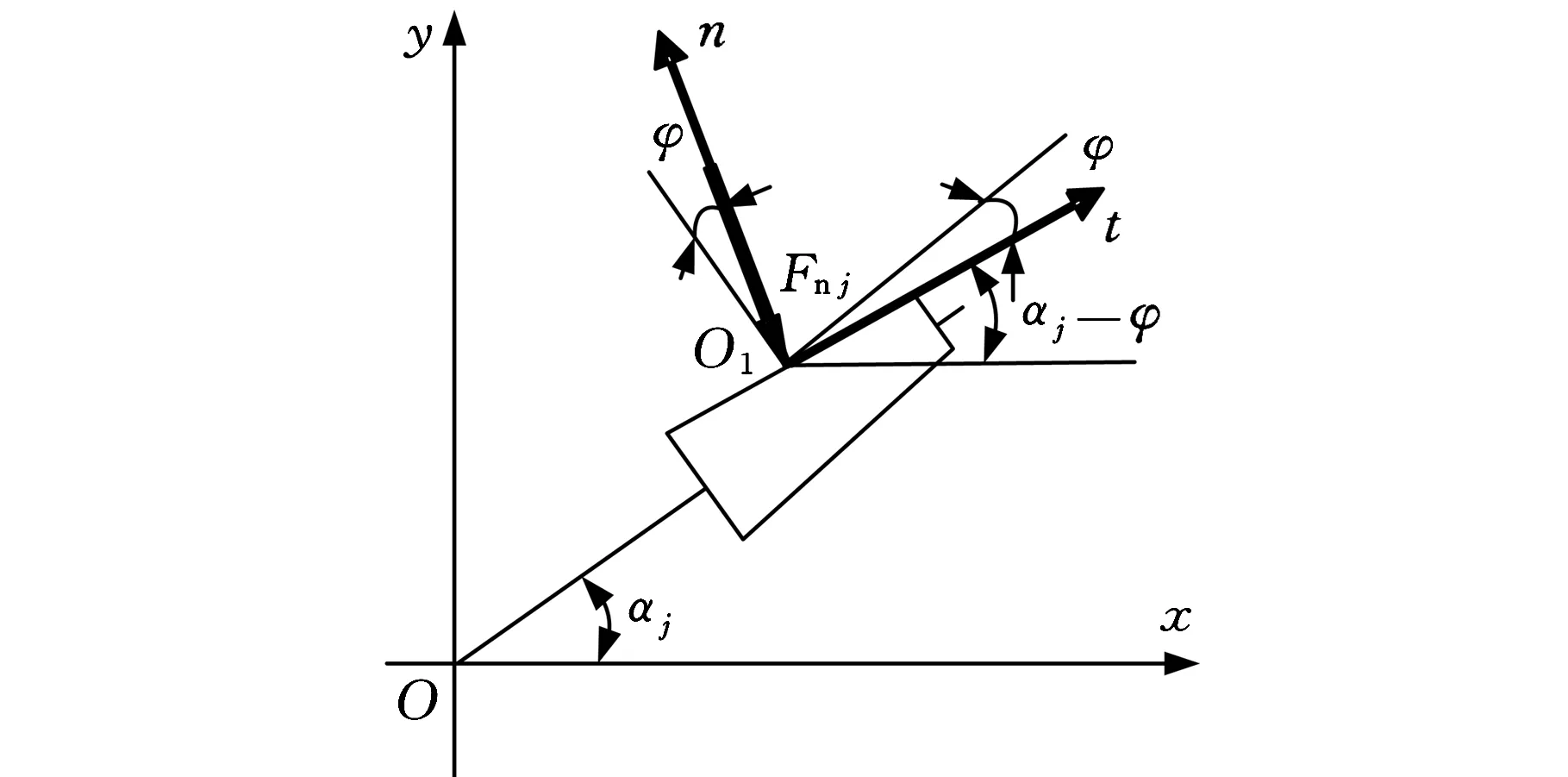
图3　轮齿受力分析图

因此,由内外齿套动态相对位移产生的法向压缩量为

Δnj2=Δn=-Δxsin(αj-φ)+

Δycos(αj-φ)

(12)

则每对齿的法向总压缩量为

(-Δxsin(αj-φ)+Δycos(αj-φ))

(13)

所以轮齿法向啮合力为

(14)

将该法向啮合力沿x轴和y轴分解，得到

(15)

因此，沿x轴和y轴的合力为

(16)

2　套齿联轴器啮合力和啮合刚度算例

2.1套齿联轴器参数

选择套齿参数[2]如表1所示。

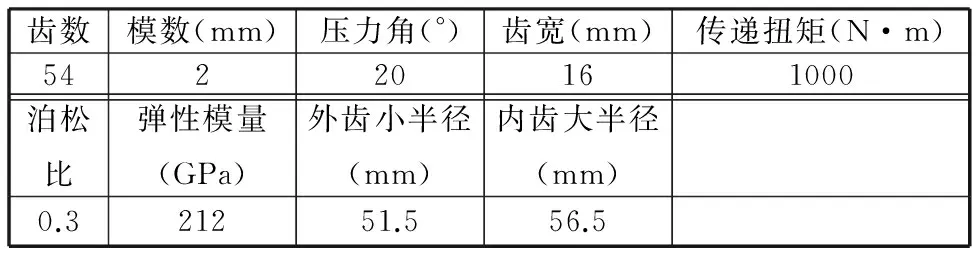
表1　套齿联轴器参数

2.2联轴器完全对中时的啮合力和啮合刚度

2.2.1不同扭矩下的啮合力和啮合刚度

计算条件如下：扭矩范围为0到5000 N·m；图4中的内外套齿的动态相对位移为x=1 μm,Δy=0;图5中,Δx=0,Δy=1 μm;内外套齿无不对中。

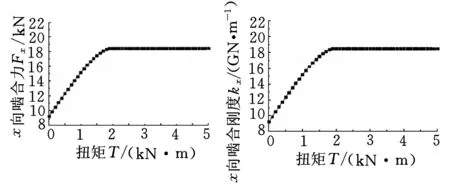
(a)啮合力(b)啮合刚度图4　扭矩对x向啮合力和啮合刚度的影响

(a)啮合力(b)啮合刚度图5　扭矩对y向啮合力和啮合刚度的影响

由图4和图5可以看出，扭矩在2000 N·m以下时,啮合力和啮合刚度随扭矩的增大而增大,当扭矩大于2000 N·m时,啮合力和啮合刚度基本不变。另外，也可以发现x向和y向具有相同的变化规律，x向的动态相对位移仅仅产生x向的啮合力，y向的动态相对位移仅仅产生y向的啮合力，联轴器不存在交叉刚度。

2.2.2内外套齿动态相对位移对啮合力和啮合刚度的影响

计算条件如下:扭矩为1000N·m;图6中,套齿动态相对位移Δx的变化范围为0～1 μm,Δy=0;图7中,Δx=0,Δy的变化范围为0～1 μm ;套齿无不对中。由图6和图7可以看出，随着动态相对位移的增大，啮合力和啮合刚度均表现出了非线性变化特征。同时，由于内外套齿不存在不对中问题，联轴器也不存在交叉刚度，即x向的动态相对位移仅仅产生x向的啮合力，y向的动态相对位移仅仅产生y向的啮合力，x向和y向具有相同的变化规律。

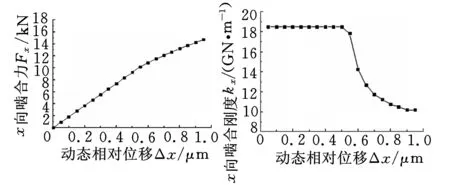
(a)啮合力(b)啮合刚度图6x向动态相对位移Δx对x向啮合力和啮合刚度的影响

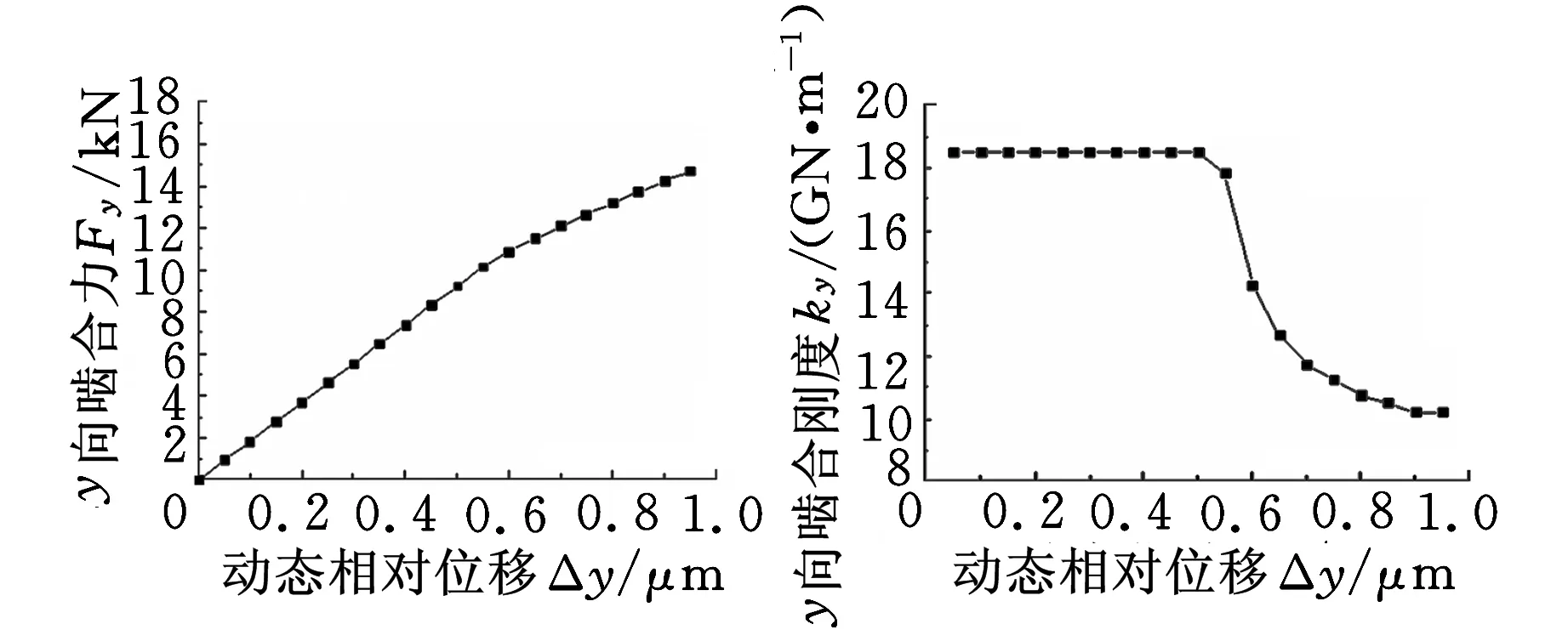
(a)啮合力(b)啮合刚度图7　y向动态相对位移Δy对y向啮合力和啮合刚度的影响

2.3存在不对中情况时的啮合力和啮合刚度

2.3.1啮合距离和单齿啮合刚度

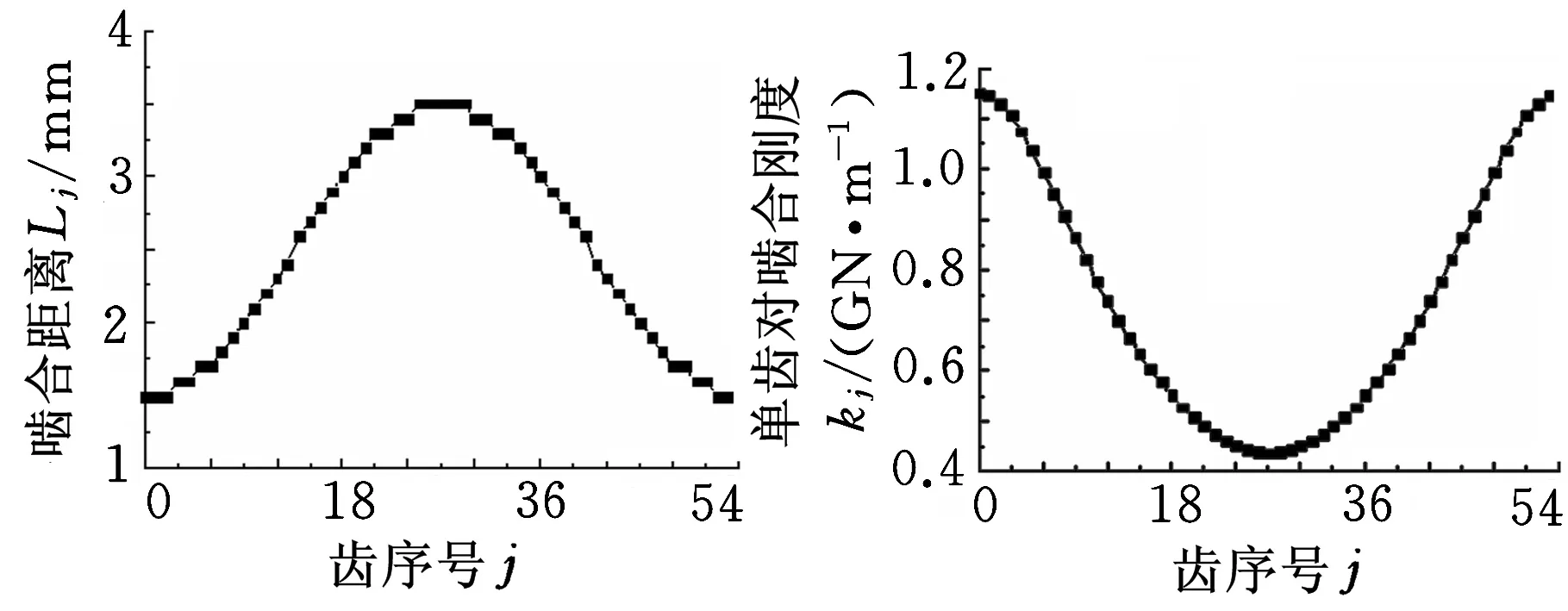
(a)啮合距离(b)啮合刚度图8　不对中对啮合距离和啮合刚度的影响

计算条件为：内外套齿不对中情况发生在x向，不对中的径向大小为1 mm,啮合距离及单齿啮合刚度随齿的变化规律如图8所示，从图8中可以看出,不存在不对中情况时,每个齿的啮合距离相等，均为2.5 mm，其中，序号从0～Z/2的齿对是由紧到松，啮合距离从1.5 mm到3.5 mm,单齿刚度由大变小；序号从Z/2～Z的齿对是由松到紧，啮合距离从3.5 mm到1.5 mm，单齿刚度由小变大。

2.3.2内外套齿不对中及动态相对位移对啮合力和啮合刚度的影响

计算条件如下：扭矩1000N·m，内外套齿不对中的径向大小e为1 mm，角度θ分别为0°、90°、180°、270°；动态相对位移Δx的变化范围为0～1 μm,Δy=0。

计算结果如图9所示，其中,图9a、图9b分别为不同的套齿不对中情况下x向、y向啮合力随动态相对位移Δx的变化规律;图9c、 图9d分别为不同的套齿不对中情况下x向、y向啮合刚度随动态相对位移Δx的变化规律。由图9可以看出,由于内外套齿不对中情况的出现，套齿刚度出现了交叉刚度，即x向的动态相对位移不仅要引起x向的啮合力，也会产生y向的啮合力,交叉刚度还可能会出现负值,刚度值随Δx出现强非线性特征。

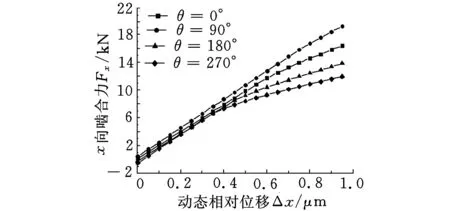
(a)x向啮合力

(b)y向啮合力

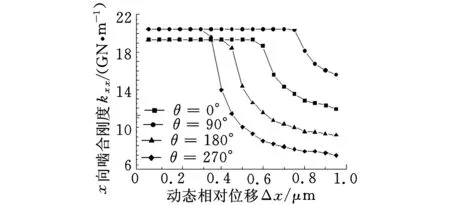
(c)x向啮合刚度kxx

(d)y向啮合刚度kyx图9　内外套齿不对中及动态相对位移Δx对套齿啮合力和啮合刚度的影响

同样,扭矩为1000N·m,不对中径向大小为1 mm,角度θ分别为0°、90°、180°、270°;动态相对位移Δy的变化范围为0～1 μm,Δx=0。计算结果如图10所示,其中,图10a、图10b分别为不同的套齿不对中的情况下x向、y向啮合力随动态相对位移Δy的变化规律;图10c、图10d分别为不同的套齿不对中的情况下x向、y向啮合刚度随动态相对位移Δy的变化规律。由图10可以看出，由于内外套齿不对中情况的出现，套齿刚度出现了交叉刚度，即y向的动态相对位移不仅会引起y向的啮合力，也会产生x向的啮合力，交叉刚度可能会出现负值，刚度值随Δy出现强非线性特征。

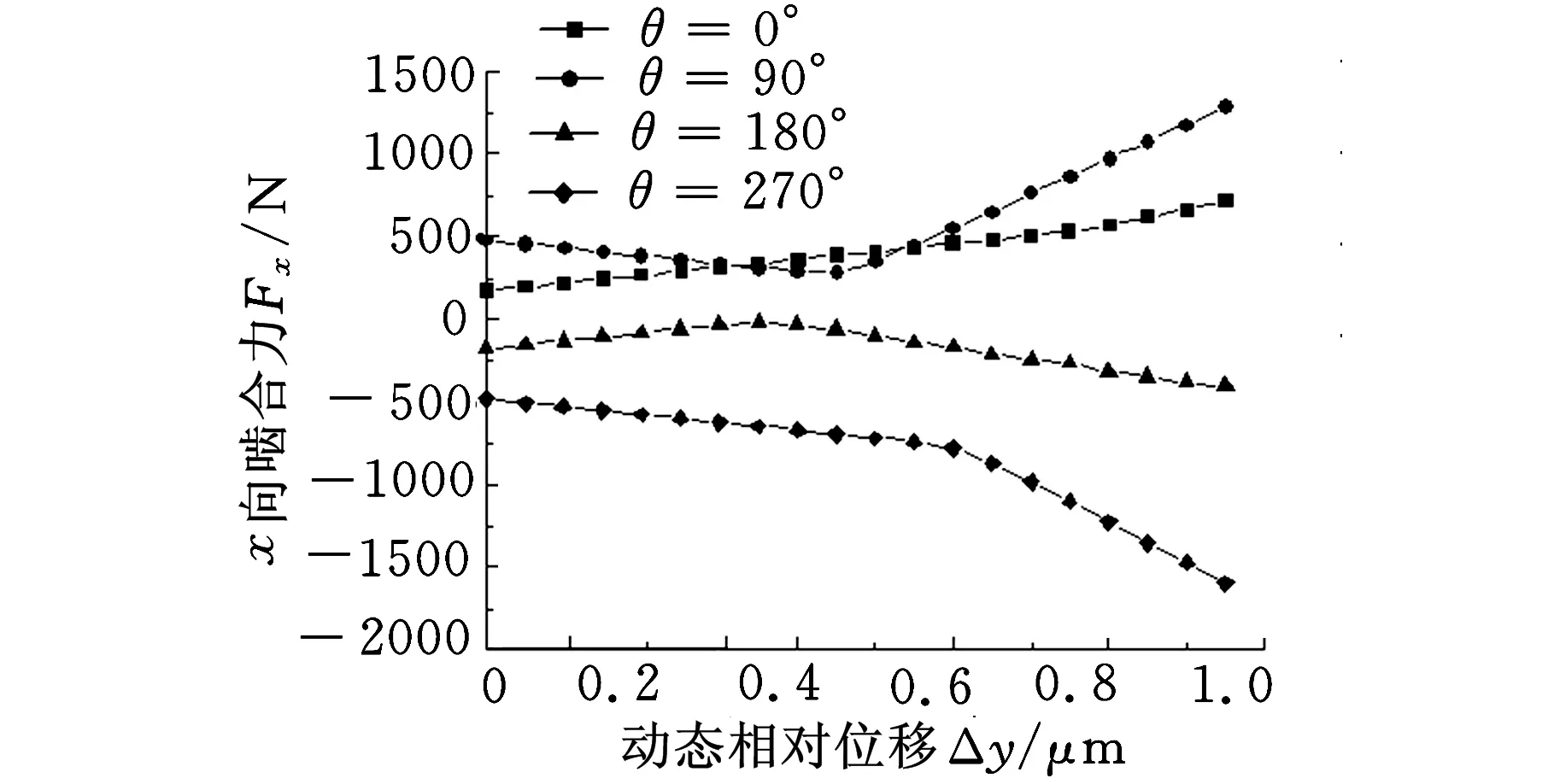
(a)x向啮合力

(b)y向啮合力

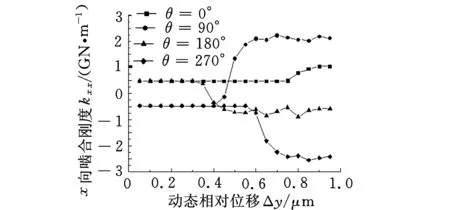
(c)x向啮合刚度kxy

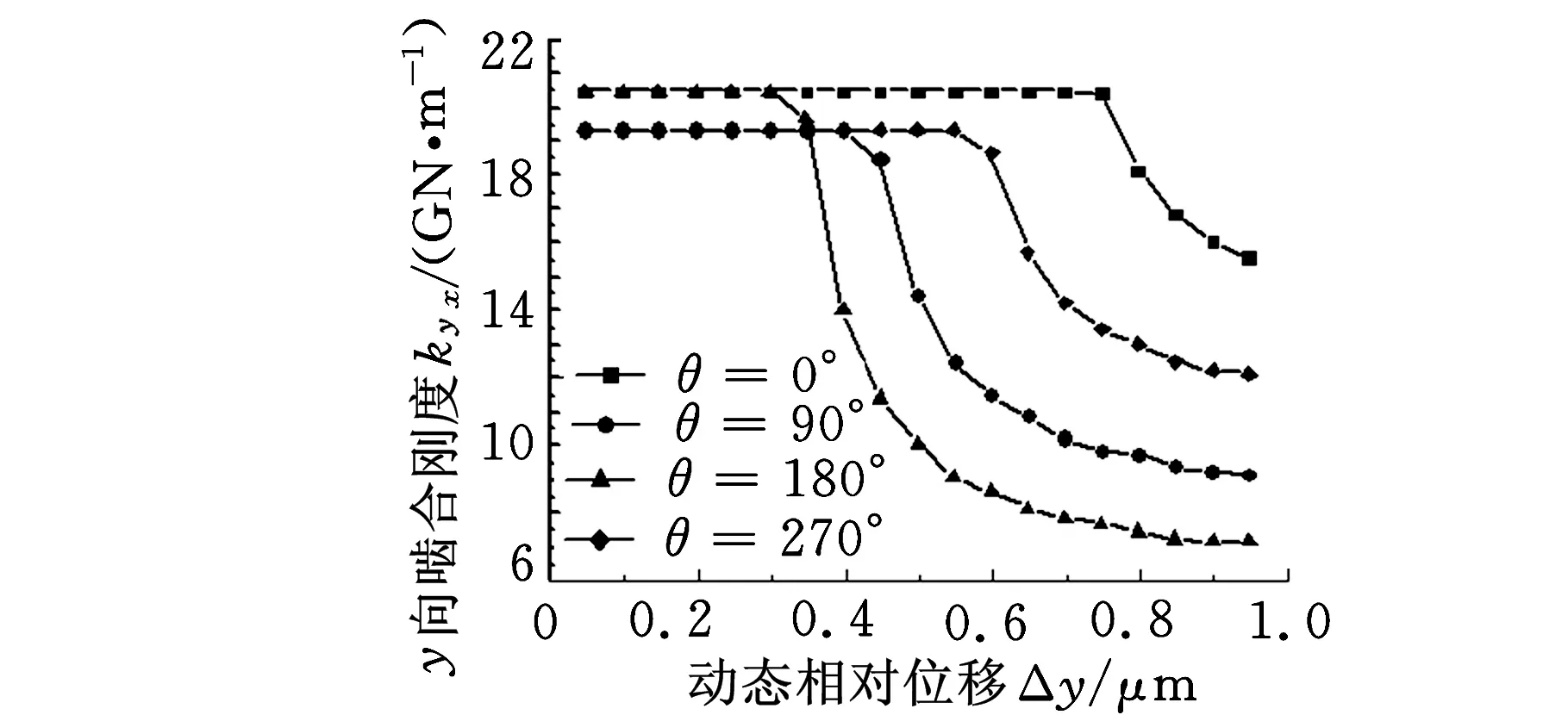
(d)y向啮合刚度kyy图10　内外套齿不对中及动态相对位移Δy对套齿啮合力和啮合刚度的影响

3　套齿联轴器刚度对转子动力特性的影响

3.1含套齿联轴器的双跨三支点转子动力学模型

为了研究套齿联轴器刚度对转子动力特性的影响，依据航空发动机套齿联轴器结构特点，建立了含套齿联轴器的双跨三支点转子动力学模型，如图11所示。

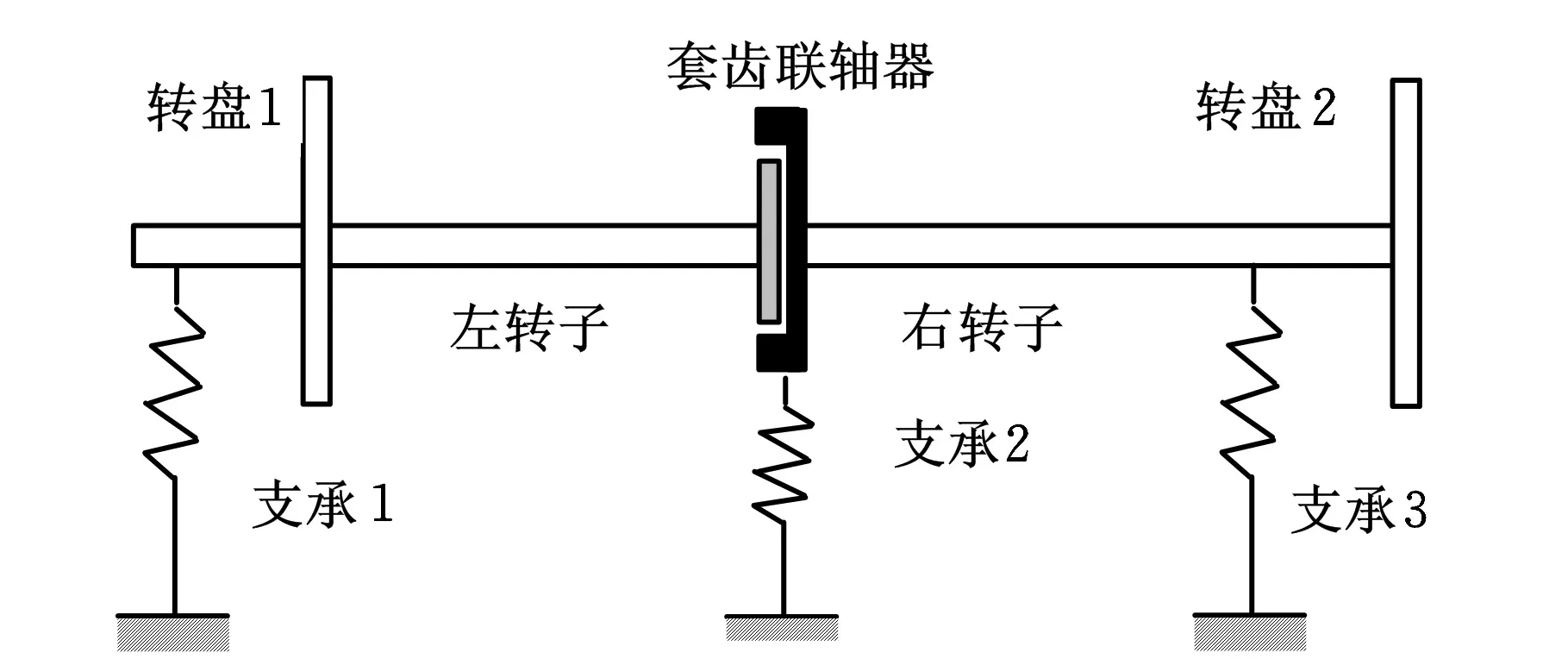
图11　含套齿联轴器三支点转子动力学模型

利用文献[12-13]提出的方法进行转子-支承系统建模和求解，该方法对转子进行有限元建模，考虑转子的转动惯量、剪切变形及陀螺力矩，定义转子与基础间的弹性支承连接、转子与转子间的联轴器连接，从而实现系统建模。限于篇幅，转子动力学模型参数从略。

3.2套齿联轴器的刚度对系统振动的影响

本文研究了系统两方面的振动特性：①通过求取系统冲击响应从而得到系统频率响应函数，其方法是在右转子的节点11施加一冲击力，通过数值积分得到系统的冲击响应，选择右转子节点1的加速度响应计算得到系统的加速度频率响应函数；②考虑左右转子的角度不对中，利用文献[14-15]中的不对中模型计算系统的不对中振动响应，设右转子为驱动轴，左转子为被驱动轴，两转子的不对中角度为1°。选取左转子转盘(节点4)的y向振动加速度响应进行分析。

3.2.1套齿联轴器的刚度分类

(1)径向等效刚度。不考虑内外套齿不对中引起的啮合距离的变化，各齿的啮合距离相同且单齿的啮合刚度均相同，通过叠加各齿对的啮合力而得到的等效刚度ke。该刚度值为定值，可由套齿参数计算得到，即

(17)

依据表1所示的套齿联轴器参数可以得到ke=18 GN/m。

(2)等效角刚度kAe表示联轴器沿横向弯曲时，每对作用的齿抵抗弯曲变形的能力:

(18)

依据表1所示的套齿联轴器参数可以得到kAe=3.95×105N·m/rad。

(3)动态啮合刚度。直接根据套齿不对中、动态相对位移、传递扭矩计算出动态啮合刚度，该刚度值是动态变化的。

3.2.2动态啮合力模型对振动特性的影响

图12所示为内外套齿不对中量e为0时，分别利用动态啮合力模型和径向等效刚度模型对系统频响函数和不对中响应计算结果的比较。图13所示为内外套齿不对中时即套齿动态相对位移分别为Δy=1 μm、Δx=1 μm时,利用动态啮合力模型的计算结果。在计算中,套齿等效刚度ke=18 GN/m;套齿角刚度均为kAe=395 kN·m/rad。

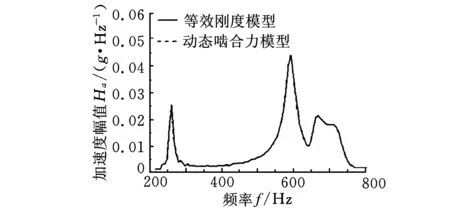
(a)幅频响应函数

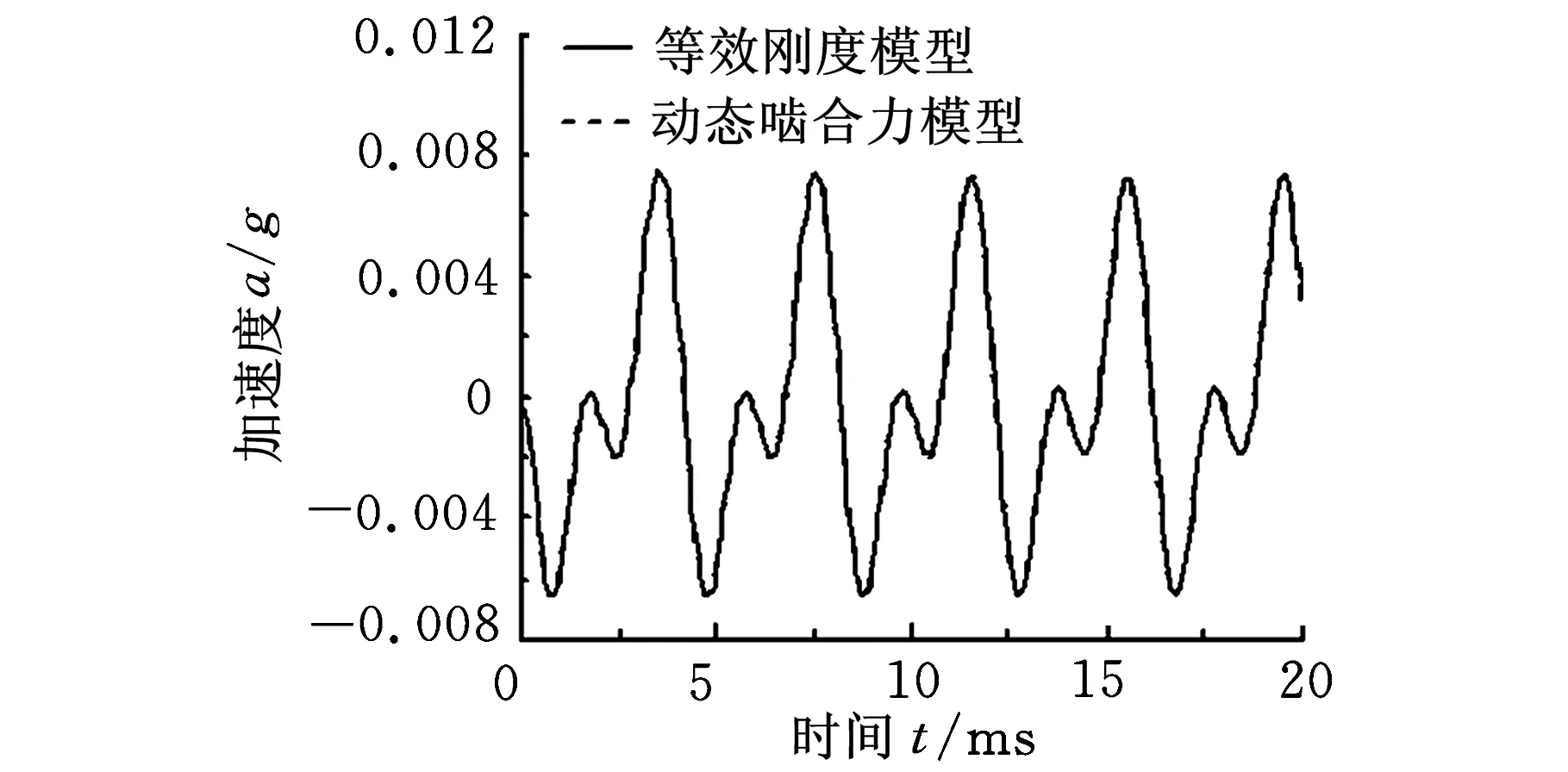
(b)角度不对中响应图12　等效刚度模型和动态啮合力模型计算结果比较

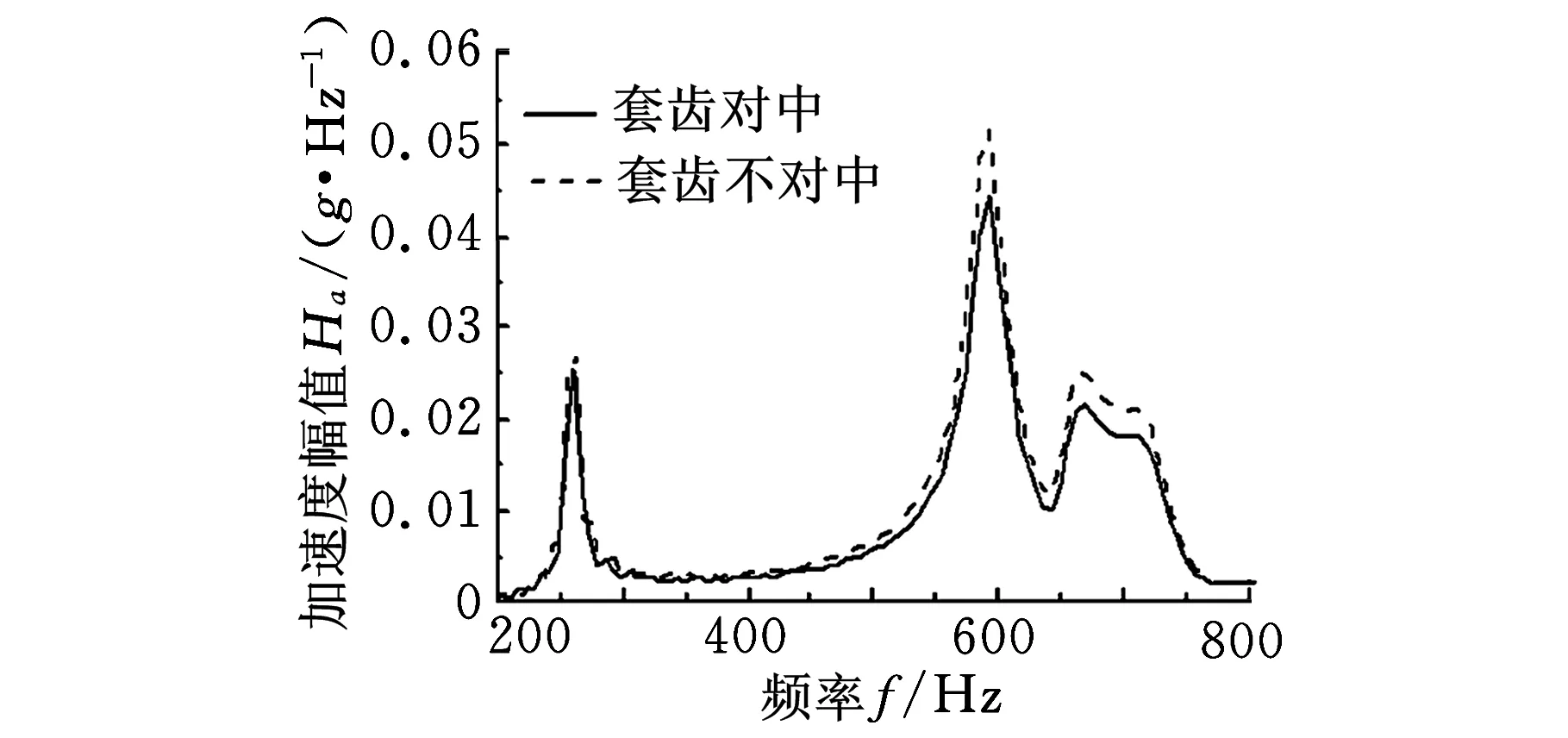
(a)幅频响应函数

(b)角度不对中响应图13　套齿不对中对系统振动特性的影响

由图12和图13可以看出，动态啮合力模型和径向等效刚度模型的计算结果几乎完全相同。内外套齿不对中对系统频响函数有一定影响，但是对不对中响应的计算结果几乎没有影响。这说明尽管内外套齿不对中和动态啮合力的变化对联轴器的刚度有影响，但还不足以影响系统的动力特性。3.2.3套齿等效刚度对系统动力特性的影响

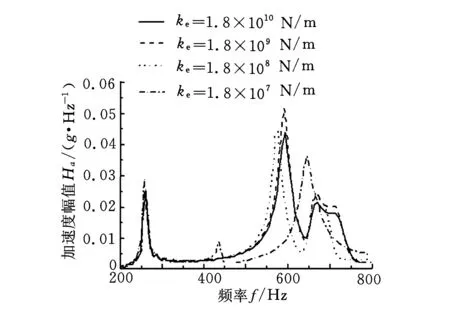
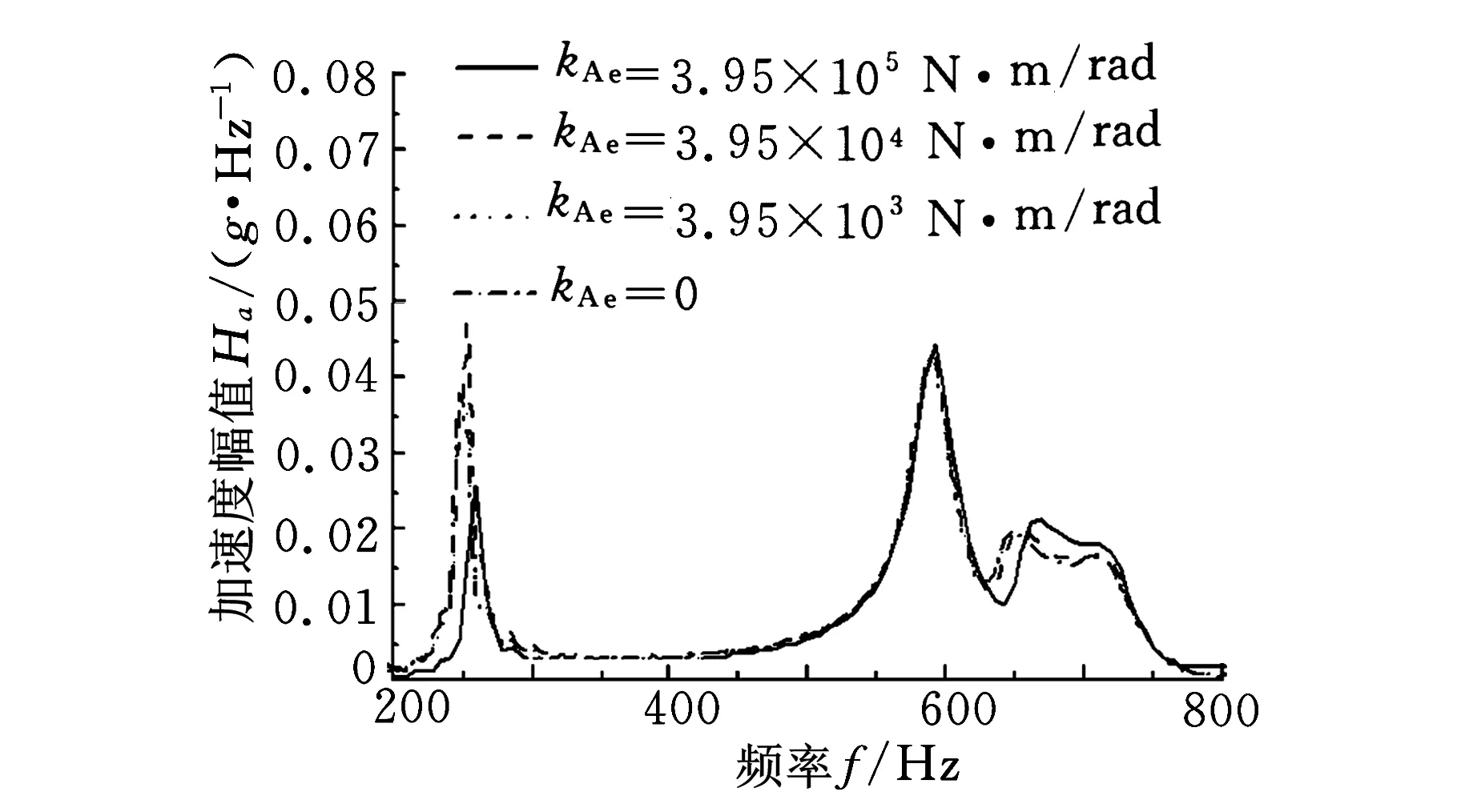
图14所示为套齿径向等效刚度ke和等效角刚度kAe对系统频响函数计算结果的比较，其中,径向等效刚度ke分别为1.8×1010N/m、1.8×109N/m、1.8×108N/m、1.8×107N/m,角刚度kAe分别为3.95×105N·m/rad、3.95×104N·m/rad、3.95×103N·m/rad、0;图15所示为

(a)等效径向刚度

(b)等效角刚度图14　等效径向刚度和等效角刚度对系统幅频率响应的影响

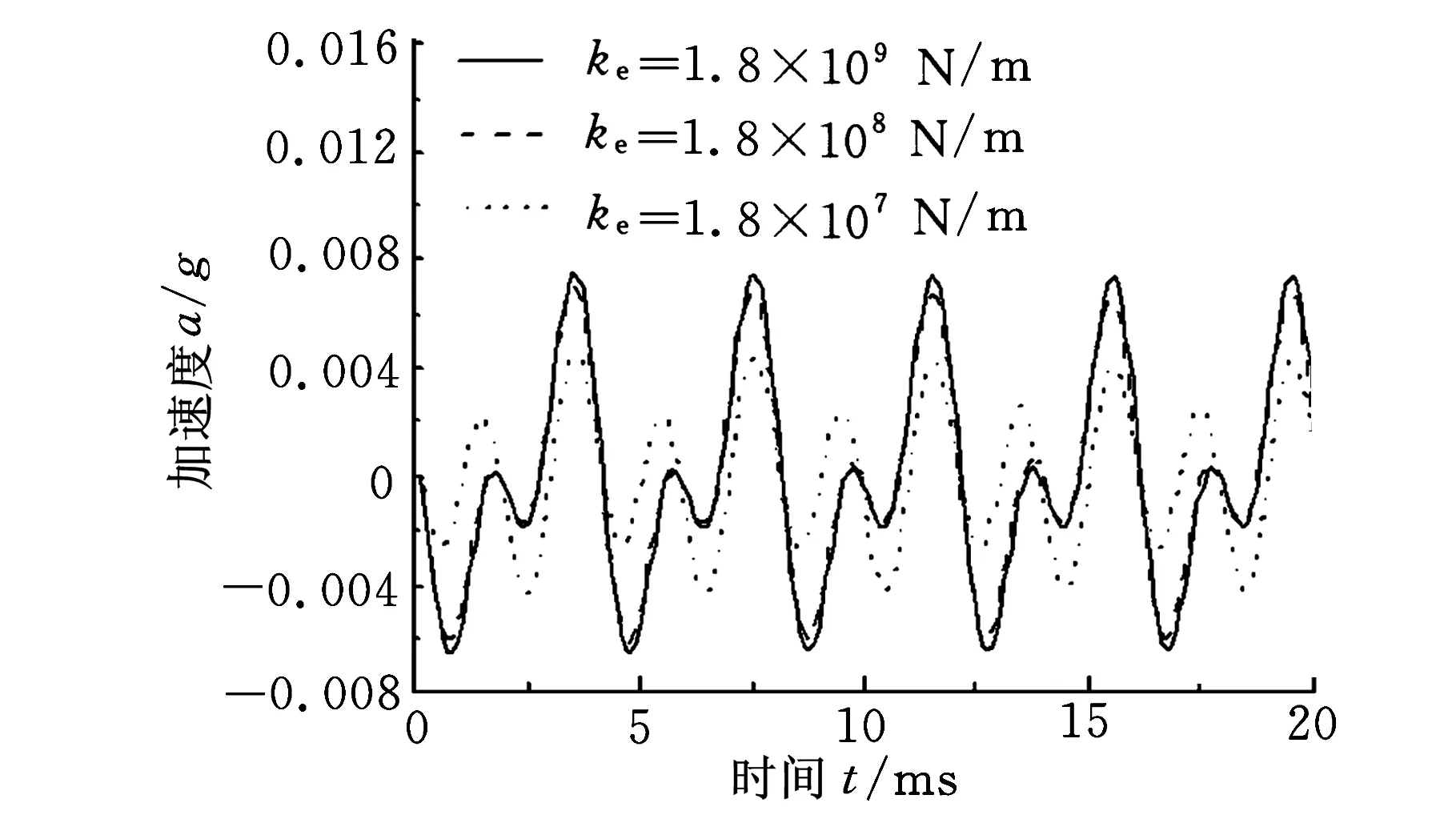
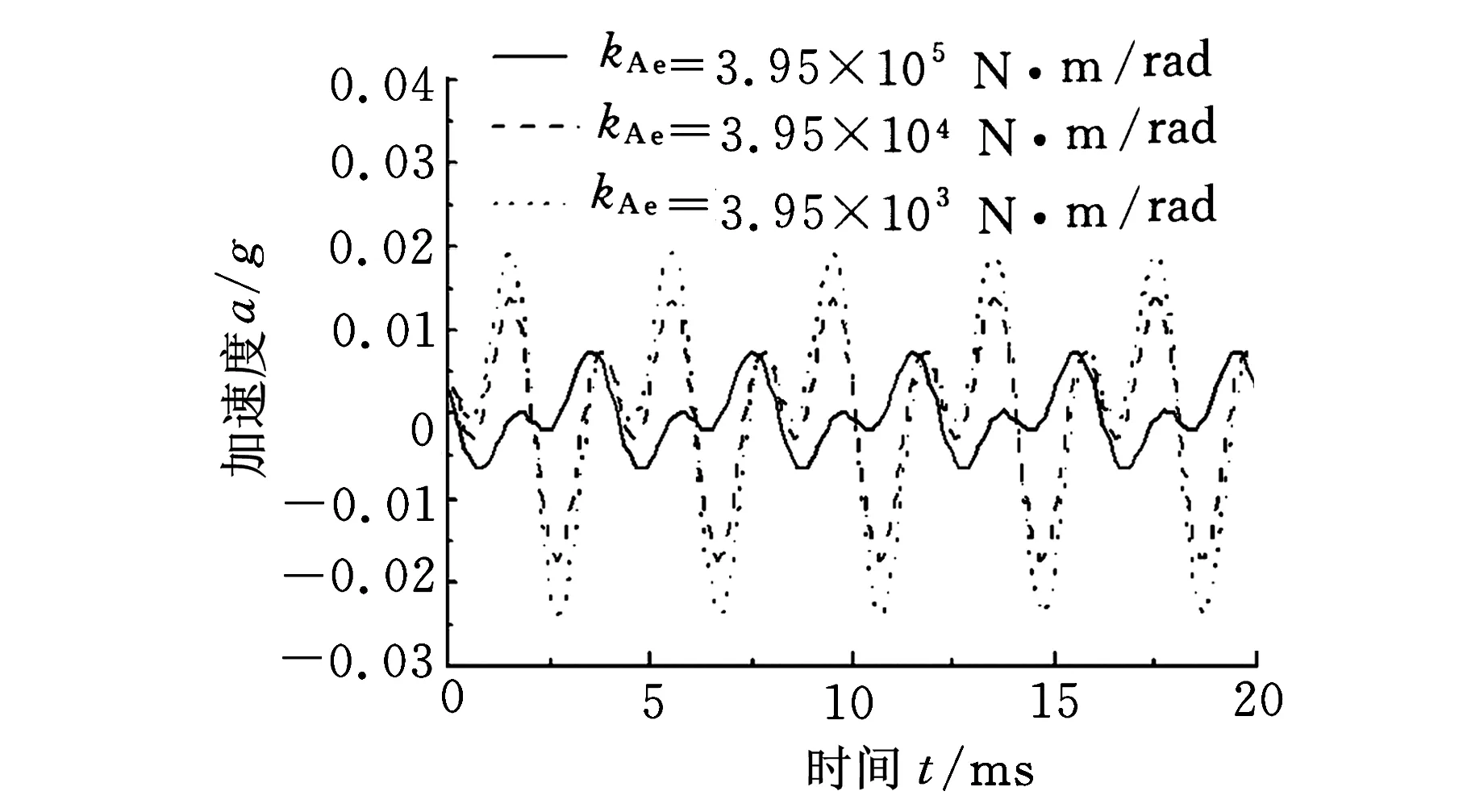
套齿径向等效刚度和等效角刚度对系统不对中响应计算结果的比较,其中,径向等效刚度ke分别为1.8×1010N/m、1.8×109N/m、1.8×108N/m,角刚度分别为kAe=3.95×105N·m/rad、3.95×104N·m/rad、3.95×103N·m/rad。

(a)等效径向刚度

(b)等效角刚度图15　等效径向刚度和等效角刚度对角度不对中响应的影响

由图14a和图15a可以看出,径向等效刚度ke为1.8×1010N/m、1.8×109N/m时对系统频响函数和不对中影响不大，随着刚度降低，频响函数和不对中响应变化均很大；由图14b和图15b可以看出，等效角刚度变化一个数量级，对系统频响函数和不对中影响均很大，这说明套齿的角刚度对系统动力学特征影响较径向等效刚度更为灵敏，因此，在设计、制造和使用中需要更多关注套齿联轴器的角刚度变化。

4　结论

(1)针对航空发动机套齿联轴器的结构形式，推导了套齿联轴器的动态啮合力计算模型。

(2)研究了套齿联轴器啮合力和啮合刚度随传递扭矩、套齿不对中和动态相对位移的变化规律，结果表明，在套齿对中情况下，啮合力和啮合刚度随扭矩和动态相对位移呈非线性变化规律，但不存在交叉刚度；但在套齿不对中情况下，啮合力和啮合刚度不仅随扭矩和动态相对位移呈非线性变化规律，还存在交叉刚度。

(3)建立了含套齿联轴器的三支点转子动力学模型，并计算了系统的频响函数和左右转子存在角度不对中时的振动响应。结果表明，动态啮合力模型与等效刚度模型计算结果基本相同，径向刚度降低两个数量级后，对计算结果影响较大，而依据动态啮合力模型得到的动态啮合的变化尚不足以引起系统动力特性的变化。需要注意的是，套齿角刚度对系统振动特性影响很大，在实际设计、装配和使用时需要引起足够的重视。

[1]航空发动机设计手册总编委会.航空发动机设计手册(第19分册)转子动力学及整机振动 [M]. 北京: 航空工业出版社,2000.

[2]刘占生, 赵广, 龙鑫. 转子系统联轴器不对中研究综述[J]. 汽轮机技术, 2007, 49(5): 321-325。

Liu Zhansheng,Zhao Guang,Long Xin.Survey of the Research on Coupling with Misalignment of Rotary Machinery[J].Turbine Technology,2007,49(5):321-325.

[3]韩捷, 石来德. 转子系统齿式联接不对中故障的运动学机理研究[J]. 振动工程学报,2004,17(4):416-420.

Han Jie, Shi Laide.Study on Kinematic Mechanism of Misalignment Fault of Rotor System Connected by Gear Coupling[J]. Journal of Vibration Engineering, 2004, 17(4): 416-420.

[4]陈果, 李兴阳. 航空发动机整机振动中的不平衡-不对中-碰摩耦合故障研究[J].航空动力学报, 2009, 24(10):2277-2284

Chen Guo,Li Xingyang.Study on Imbalance-misalignment-rubbing Coupling Faults in Aero-engine Vibration [J].Journal of Aerospace Power,2009,24(10):2277-2284.

[5]龙鑫. 齿式联轴器不对中动力学特性研究[D]. 哈尔滨：哈尔滨工业大学, 2006.

[6]赵广.转子-联轴器-轴承-隔振器系统耦合动力学特性研究[D]. 哈尔滨：哈尔滨工业大学, 2009.

[7]Lee Y S,Lee C W.Modelling and Vibration Analysis of Misaligned Rotor-ball Bearing Systems[J].Journal of Sound and Vibration,1999,224(1):17-32.

[8]Ai-Hussain K M,Redmond I.Dynamic Response of Two Rotors Connected by Rigid Mechanical Coupling with Parallel Misalignment [J].Journal of Sound and Vibration,2002,249(1):483-498.

[9]Al-Hussain K M,Redmond I.Dynamic Stability of Two Rigid Rotors Connected by a Flecible Coupling with Augular Misalignment[J].Journal of Sound and Vibration,2003,266(2):217-234.

[10]Li M,Yu L.Analysis of the Coupled Lateral Vibration of a Rotor-bearing-system with a Misaligned Gear Coupling[J].Journal of Sound and Vibration,2001,243(2):283-300.

[11]李明. 齿轮联轴器不对中转子系统的稳态振动特征分析[J]. 机械强度, 2002, 24(1): 52-55.

Li Ming.Analysis on the Steady State Vibration Properties of Rotor Systems Connected with Misaligend Gear Coupling[J].Journal of Mechanical Strength,2002, 24(1):52-55.

[12]陈果.双转子航空发动机整机振动建模与分析[J]. 振动工程学报, 2011, 24(6): 619-632.

Chen Guo.Vibration Modeling and Analysis for Dual-rotor Aero-engine[J]. Journal of Vibration Engineering, 2011,24(6): 619-632.

[13]陈果. 航空发动机整机振动耦合动力学新模型及其验证[J]. 航空动力学报, 2012, 27(2): 241-254.

Chen Guo.A Coupling Dynamic Model for Whole Aero-engine Vibration and Its Verification[J].Journal of Aerospace Power,2012,27(2): 241-25.

[14]Xu M,Marangoni R D.Vibration Analysis of a Motor-flexible Coupling-rotor System Subject to Misalignment and Unbalance,PART I:Theoretical Model and Analysis[J].Journal of Sound and Vibration, 1994, 176(5): 663-679.

[15]Xu M, Marangoni R D. Vibration Analysis of a Motor-flexible Coupling-rotor System Subject to Misalignment and Unbalance,PART Ⅱ:Experimental Validation[J].Journal of Sound and Vibration,1994,176(5):681-691.

(编辑苏卫国)

Effects of Gear Coupling on Aero-engine Vibration Characteristics

Liao Zhongkun1Chen Guo2Wang Haifei2

1.Beijing Power Machine Research Institute,Aeronautics and Astronautics Technique Research Institute of China,Beijing,100074 2.Nanjing University of Aeronautics and Astronautics,Nanjing,211106

The aero-engine gear coupling stiffness was studied herein,and the coupling dynamic gearing forces were deduced,the relationship among the gear coupling gearing forces and the torque,misalignment,and the dynamic relative displacements was analyzed.According to aero-engine gearing structure characteristics,a rotor dynamic model including gear coupling and the three supports was established,and the effects of gear coupling stiffness on the system frequency response function were analyzed;under the conditions of considering the angle misalignment between two rotors,the effects of gear stiffness on the misalignment responses were studied.The results show that the dynamic gearing stiffness model can simulate the gear coupling dynamic stiffness very correctly,but the dynamic change range of the stiffness is not enough to change obviously the system dynamic characteristics,however,the effects of the angle stiffness of gear coupling on the system vibration characteristics are very great.

aero-engine;gear coupling;gearing stiffness;misalignment;vibration characteristics

2013-12-30

国家自然科学基金资助项目(50705042);航空科学基金资助项目(2007ZB52022)

V232DOI：10.3969/j.issn.1004-132X.2015.10.007

廖仲坤,男,1974年生。中国航天飞航技术研究院北京动力机械研究所高级工程师。主要研究方向为航空发动机结构设计与振动分析。陈果,男,1972年生。南京航空航天大学民航学院教授、博士研究生导师。王海飞，男，1986年生。南京航空航天大学民航学院博士研究生。