2015高考万有引力与航天类试题评析

章克文

摘   要：本文对2015高考物理试卷中与万有引力相关的试题进行分类分析，探索并形成应对万有引力与航天类考题的教学策略。

关键词：万有引力;高考题;模型

中图分类号：G633.7 文献标识码：A    文章编号：1003-6148（2015）9-0045-3

“万有引力与航天”是高考中的重点和难点，同时也是学生感到棘手的问题之一。在刚刚结束的2015高考中，全国各地考卷均考查了该考点。现对2015高考中此类考题做一总结，希望对以后的高考复习有所帮助。

1    “中心天体-环绕天体”模型

此模型中，中心天体对环绕天体的引力充当环绕天体做圆周运动的向心力。对环绕天体的运行参量进行比较和运算，可分为两种类型：一类是不同的中心天体，另一类是同一个中心天体。

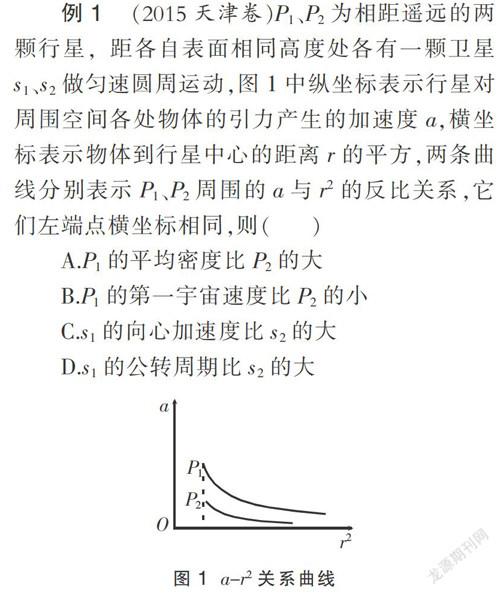
例1  （2015天津卷）P1、P2为相距遥远的两颗行星，距各自表面相同高度处各有一颗卫星s1、s2做匀速圆周运动，图1中纵坐标表示行星对周围空间各处物体的引力产生的加速度a，横坐标表示物体到行星中心的距离r的平方，两条曲线分别表示P1、P2周围的a与r2的反比关系，它们左端点横坐标相同，则（     ）

A.P1的平均密度比P2的大

B.P1的第一宇宙速度比P2的小

C.s1的向心加速度比s2的大

D.s1的公转周期比s2的大

解析  本题两颗卫星对应的是不同的中心天体。由a-r2坐标图可知，两颗行星（中心天体）的半径相同，s1的向心加速度比s2的大。由a=G可知，P1的质量大于P2的质量，P1的平均密度比P2的大，两颗卫星的轨道半径相同。由G=m，可得T=2π，中心天体质量大的卫星周期小。A、C选项正确。

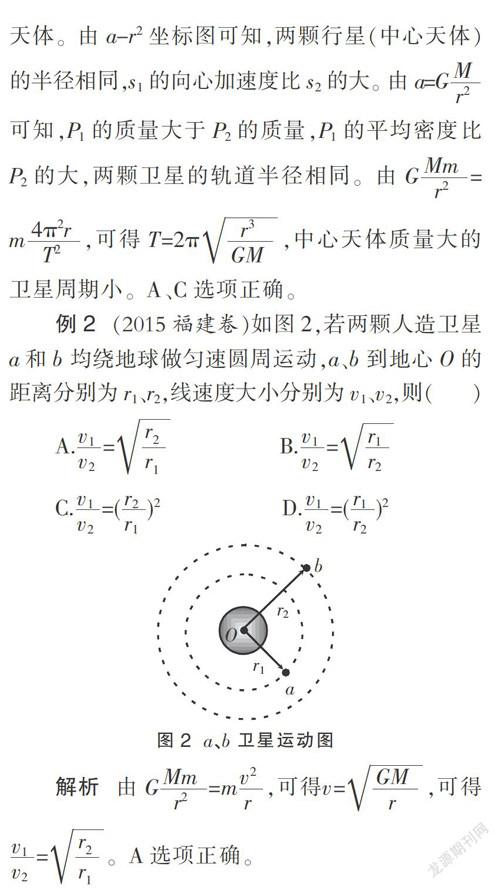
例2  （2015福建卷）如图2，若两颗人造卫星a和b均绕地球做匀速圆周运动，a、b到地心O的距离分别为r1、r2，线速度大小分别为v1、v2，则（     ）

A.=              B.=

C.=（）2                D.=（）2

解析  由G=m，可得v=，可得=。A选项正确。

点评  考察不同中心天体的还有2015年的江苏高考题。考察同一中心天体的还有2015年的北京卷和四川卷。在解这两类试题时要区分清楚这个不同点，如果是同一中心天体如例2，在运算时可以把中心天体约掉，如果是不同的中心天体就不能约，这一点一定要分清。

2    天体表面物体模型

例3  （2015海南卷）若在某行星和地球上相对于各自水平地面附近相同的高度处，以相同的速率平抛一物体，它们在水平方向运动的距离之比为2：。已知该行星质量约为地球的7倍，地球的半径为R，由此可知，该行星的半径为（   ）

A.R    B.R     C.2R     D.R

解析  水平方向x=v0t，竖直方向h=gt2，得g=，又由黄金代换式GM=gR2，可得R2=，带入数据可得C选项正确。

点评  本题要用到两方面知识：平抛运动和天体表面物体模型。天体表面物体在忽略天体自转的情况下，重力等于万有引力，可得到黄金代换式。有时还要结合“中心天体-环绕天体模型”才能求解，例如2015年的新课标I卷。

跟踪练习1：（2015新课标I卷 ）我国发射的“嫦娥三号”登月探测器靠近月球后，先在月球表面附近的近似圆轨道上绕月运行;然后经过一系列过程，在离月面4 m高处做一次悬停（可认为是相对于月球静止）;最后关闭发动机，探测器自由下落。已知探测器的质量约为1.3×103 Kg，地球质量约为月球的81倍，地球半径约为月球的3.7倍，地球表面的重力加速度大约为9.8 m/s2，则此探测器（      ）

A.在着陆前的瞬间，速度大小约为8.9 m/s

B.悬停时受到的反冲作用力约为2×103 N

C.从离开近月圆轨道到着陆这段时间内，机械能守恒

D.在近月圆轨道上运行的线速度小于人造卫星在近地圆轨道上运行的线速度

答案：B、D。

3   多星模型

宇宙中多个天体依靠彼此间的相互作用围绕同一点做圆周运动的模型，例如双星、三星、四星、多星模型等。多星问题依然遵循万有引力定律和牛顿运动定律。

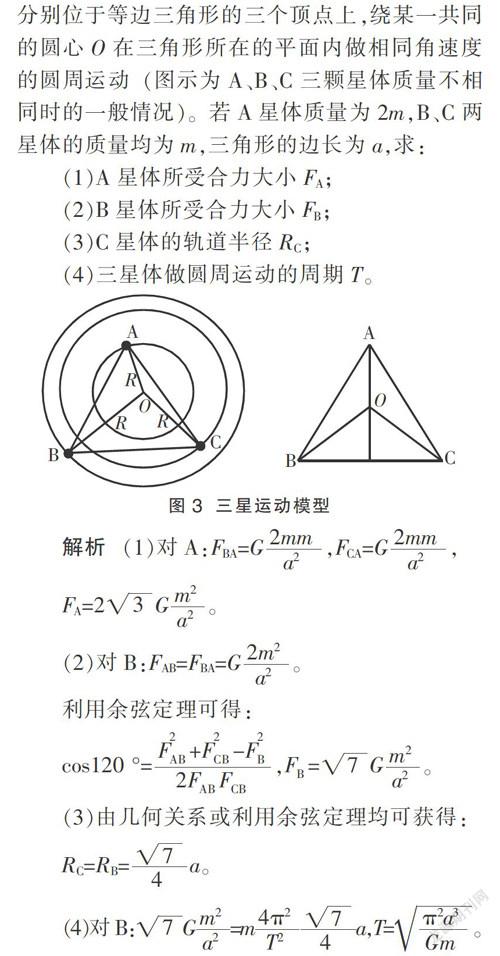
例4  （2015安徽卷）由三颗星体构成的系统，忽略其他星体对它们的作用，存在着一种运动形式：三颗星体在相互之间的万有引力作用下，分别位于等边三角形的三个顶点上，绕某一共同的圆心O在三角形所在的平面内做相同角速度的圆周运动（图示为A、B、C三颗星体质量不相同时的一般情况）。若A星体质量为2m，B、C两星体的质量均为m，三角形的边长为a，求：

（1）A星体所受合力大小FA;

（2）B星体所受合力大小FB;

（3）C星体的轨道半径RC;

（4）三星体做圆周运动的周期T。

解析  （1）对A：FBA=G，FCA=G，

FA=2G。

（2）对B：FAB=FBA=G。

利用余弦定理可得：

cos120 °=，F=G。

（3）由几何关系或利用余弦定理均可获得：

RC=RB=a。

（4）对B：G=ma，T=。

点评  不论三星、四星还是多星模型，解决问题的关键还是找准每一做圆周运动的研究对象所需向心力的来源，并结合牛顿第二定律列好动力学方程。当然在解题过程中，基本的几何分析能力和运算能力还是不可少的。今年的上海卷考察了双星模型。

跟踪练习2：（2015上海卷）两靠得较近的天体组成的系统称为双星，它们以两者连线上某点为圆心做匀速圆周运动，因而不至于由于引力作用而吸引在一起。设两天体的质量分别为m和m，则它们的轨道半径之比R∶R=_________;速度之比v∶v=_________。

答案：m∶m;m∶m。

4    太空生活模型

随着科技的发展，在太空中生活已不是遥不可及的事情。今年的天津考题就给我们描绘了这样一幅场景。

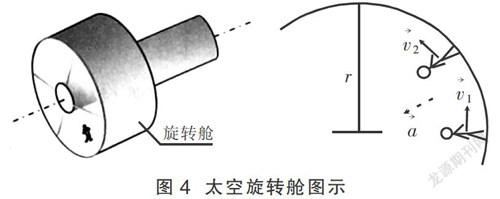
例5 （2015天津卷）未来的星际航行中，宇航员长期处于零重力状态。为缓解这种状态带来的不适，有人设想在未来的航天器上加装一段圆柱形“旋转仓”，如图4所示。当旋转舱绕其轴线匀速旋转时，宇航员站在旋转舱内圆柱形侧壁上，可以受到与他站在地球表面时相同大小的支持力。为达到目的，下列说法正确的是（     ）

A.旋转舱的半径越大，转动的角速度就应越大

B.旋转舱的半径越大，转动的角速度就应越小

C.宇航员质量越大，旋转舱的角速度就应越大

D.宇航员质量越大，旋转舱的角速度就应越小

解析   众所周知，失重并不是重力消失了，而是支持力发生了变化。物理学中把这个支持力称为“表观重量”。在太空航行中宇航员处于完全失重的状态，并不是不受到引力，而是不受到支持力，从而会感到不适。要解决这个问题只要能让宇航员和航天器的地板之间产生支持力即可。结合圆周运动所学知识，让航天器旋转起来，宇航员随航天器一起做圆周运动，地板对宇航员的支持力提供宇航员做圆周运动所需向心力。当支持力的大小和宇航员在地面所受支持力大小一致时，失重感即会消失。根据F=mω2r=mg，g=ω2r。可知角速度大则半径小，角速度小则半径大，与宇航员质量无关。选项B正确。

5    “月地拉格朗日点”轨道模型

拉格朗日点是指：一个小物体在两个大物体的引力作用下，在空间中存在着一些点，在这些点处，小物体相对于两个大物体基本保持静止（即运转的角速度相同）。

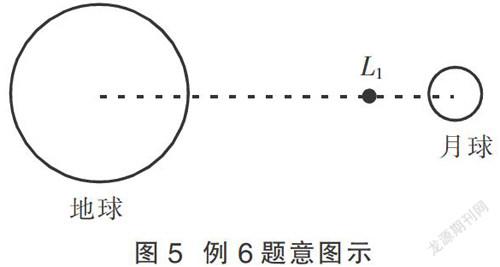
例6  （2015山东卷）如图5，拉格朗日点L1位于地球和月球连线上，处在该点的物体在地球和月球引力的共同作用下，可与月球一起以相同的周期绕地球运动。据此，科学家设想在拉格朗日点L1建立空间站，使其与月球同周期绕地球运动。以a1、a2分别表示该空间站和月球向心加速度的大小，a3表示地球同步卫星向心加速度的大小。以下判断正确的是（     ）

A.a2>a3>a1        B.a2>a1>a3

C.a3>a1>a2        D.a3>a2>a1

解析  解本题的关键点是审清题目信息，拉格朗日点L1处的空间站和月球绕地球的周期相同，即角速度相同。月球半径大，月球向心加速度大。月球的公转周期大于同步卫星周期，可以得到同步卫星向心加速度比月球大，选项D正确。

点评  地球-月球的拉格朗日点是登月的必经之路，非常适合建造地月间的旅行中转站，占领这个位置，就抢占了通往月球的咽喉，这对于月球的开发具有非常重要的意义。在2012年江苏卷中考核过“日地拉格朗日点”轨道模型。

6    总   结

万有引力与航天，历来都是考生觉得比较难的一个知识模块，究其原因：①学生的实际生活与这一知识模块接触不多，缺少直接的感官认识。②本章在某种意义上来讲是上一章曲线运动的深化运用。因此，上一章的学习如果不是非常顺利的话，那么在这一章中自然也就困难重重。要牢固掌握本章内容，并熟练地运用到各种实际模型中去，笔者认为可以从以下几个方面来做：

1）夯实基础，抓牢根本

即便是在高考中，基本知识点的考核也是占到了很大的比例。因此，抓牢基本知识点是学好各类知识的首要条件。

2）简化问题，透过现象看本质

查阅各类资料，可以发现对本章所涉及的模型分类众多。但笔者认为最关键的还是要透过现象看本质。如果考生能够熟练地找到向心力来源，列出动力学方程，那么题目再怎么变，也能以不变应万变。

3）结合实际，活学活用

现在，与时俱进这个理念已经深入到我们生活中的方方面面，高考亦然。现在的高考考题往往都会把书本知识与最新的科学研究成果进行整合，以一个全新的面目呈现到考生面前。因此，了解最新的科研成果，做到结合实际，活学活用也是考生们和老师们需要关注的一个方面。

（栏目编辑    陈   洁）