对一道常见习题解法的纠正
刘远辉


摘 要:指出通常资料上对一道圆周运动中的临界问题的错误解法,并通过严谨分析,给出正确完整的解法。
关键词:匀速圆周运动;圆盘;最大静摩擦力;相对滑动
中图分类号:G633.7 文献标识码:A 文章编号:1003-6148(2015)9-0040-2
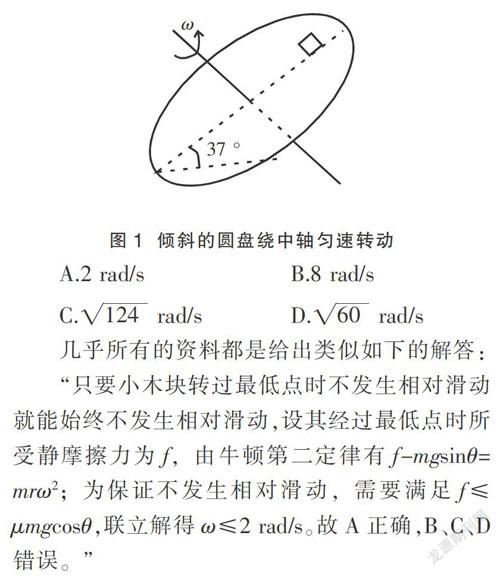
在很多教学资料中,常出现这样一道题:如图1所示,倾斜放置的圆盘绕着中轴匀速转动,圆盘的倾角为37 °,在距转动中心r=0.1 m处放一个小木块,小木块跟随圆盘一起转动,小木块与圆盘间的动摩擦因数μ=0.8,假设木块与圆盘的最大静摩擦力与相同条件下的滑动摩擦力相同。若要保持小木块不相对圆盘滑动,圆盘转动的角速度最大不能超过( )
A.2 rad/s B.8 rad/s
C. rad/s D.rad/s
几乎所有的资料都是给出类似如下的解答:
“只要小木块转过最低点时不发生相对滑动就能始终不发生相对滑动,设其经过最低点时所受静摩擦力为f,由牛顿第二定律有f-mgsinθ=mrω2;为保证不发生相对滑动,需要满足f≤μmgcosθ,联立解得ω≤2 rad/s。故A正确,B、C、D错误。”
上述解法的前提是:“只要小木块转过最低点时不发生相对滑动就能始终不发生相对滑动”,只要知道了这个前提,接下来的解答过程就简单了,只要按照上述资料的解法就可以了。但是,这个前提是怎么来的呢?几乎所有资料的解答都没有给出。笔者认为,此题应从一般情况入手分析,才够严谨。解答过程如下:
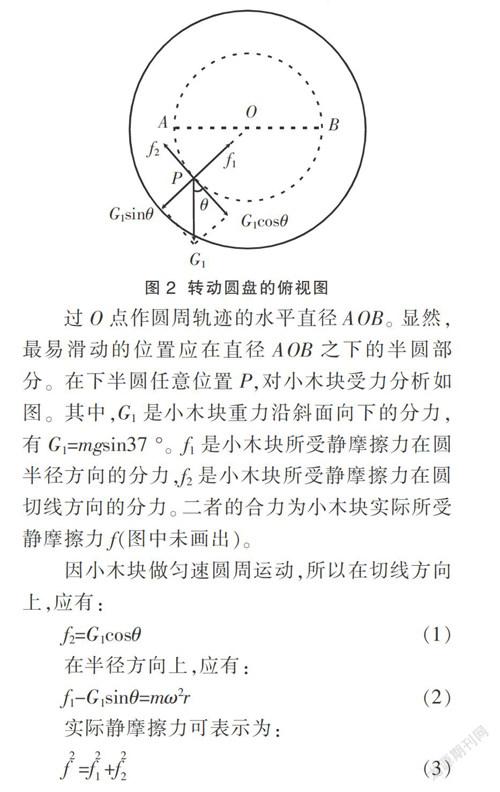
解析:作沿转轴方向的俯视图,如图2所示。
过O点作圆周轨迹的水平直径AOB。显然,最易滑动的位置应在直径AOB之下的半圆部分。在下半圆任意位置P,对小木块受力分析如图。其中,G1是小木块重力沿斜面向下的分力,有G1=mgsin37 °。f1是小木块所受静摩擦力在圆半径方向的分力,f2是小木块所受静摩擦力在圆切线方向的分力。二者的合力为小木块实际所受静摩擦力f(图中未画出)。
因小木块做匀速圆周运动,所以在切线方向上,应有:
f2=G1cosθ(1)
在半径方向上,应有:
f1-G1sinθ=mω2r (2)
实际静摩擦力可表示为:
f=f+f(3)
设最大静摩擦力为fm,则应有:
f2≤f(4)
再结合(1)(2)(3)式,可得:
(G1sinθ+mω2r)2+(G1cosθ)2≤f,
其中,fm=μmgcos37 °。
将所有已知数据代入后,并化简可得方程:
ω4+120sinθω2-496≤0
或sinθ≤(5)
依照题意,θ的取值范围是0≤θ≤90 °,因而0≤sinθ≤1。欲使(5)式恒成立(即小木块相对圆盘始终静止),只需1≤,或ω4+120ω2-496≤0。
此不等式的解为:0≤ω2≤4。
所以,小木块的角速度的取值范围应该是:0≤ω≤2 rad/s。显然角速度的最大值为2 rad/s,且此时对应的sinθ=1,即θ=90 °。也就是说,小木块在最低点位置时最易滑动,且在ω=2 rad/s时开始滑动。本题选A,解毕。
如果按照上述完整解法来解决此题,难度较大。但如果因为难度大,就忽略了对问题的严谨分析,而是粗略地认为最低点先达到最大静摩擦力,显然不利于培养学生严谨思考的习惯。所以笔者建议,在日常教学中,为学生选题要慎重,给学生留作业之前教师自己应该先做一遍。
参考文献:
[1]物理课程教材研究开发中心 课程教材研究所·物理·必修2[M].北京:人民教育出版社,2010.
[2]孙慧.物体做圆周运动的向心力[J].物理教学探讨,2007,25(3):11-13,15.
(栏目编辑 罗琬华)

